5.2不等式的性质

课件29张PPT。5.2 不等式的性质义务教育课程标准实验教科书　
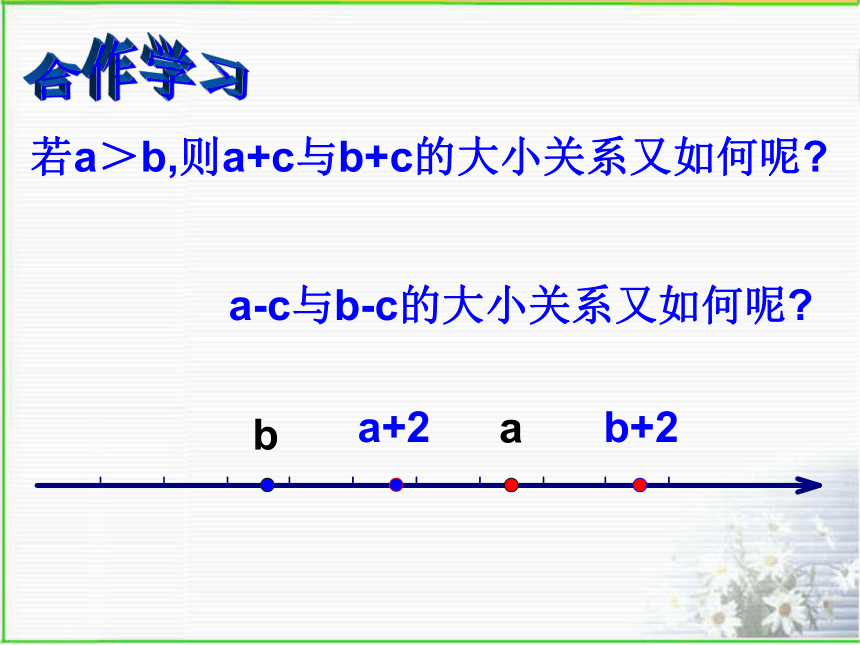
浙江版《数学》八年级上册合作学习若a＜b,而b＜c,则a与c的大小关系是baca＜c不等式的基本性质1若a＜b, b＜c. 则a＜c也称为不等式的传递性若 a＜b, b＜2a-1, 则 a 2a-1＜合作学习若a＞b,则a+c与b+c的大小关系又如何呢?a-c与b-c的大小关系又如何呢?baa+2b+2不等式的基本性质2不等式的两边都加上(或减去)同一
数或式,所得的不等式仍成立.如果a＞b ,那么a + c＞b + c , a-c＞b - c如果a＜b ,那么a + c＜b + c , a-c＜b - c试一试比较下列大小 8＿＿12
8×4＿＿12×4
8÷4＿＿12÷4
8×(-4)＿＿12×(-4)
8÷(-4)＿＿12÷(-4) (-4)＿＿(-6)
(-4)×2＿＿(-6)×2
(-4)÷2＿＿(-6)÷2
(-4)×(-2)＿＿(-6)×(-2)
(-4)÷(-2)＿＿(-6)÷(-2)
＜＜＜＜＜＞＞＞＞＞想一想:从上面的变化,你发现了什么?⑴、不等式的两边都乘以(或除以)同一个正数，所得的不等式仍成立；⑵、不等式的两边都乘以(或除以)同一个负数，必须把不等号的方向改变，所得的不等式成立.不等式的基本性质：性质3：不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立；
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.性质1：若a＜b，b＜c，则a＜c。性质2：不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.（不等号方向不变）（不等号方向不变）（不等号方向改变）（传递性）不等式的基本性质：性质1：若a＜b，b＜c，则a＜c。
性质2：不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
如果a＞b,那么a+c＞b+c,a-c＞b-c.
如果a＜b,那么a+c＜b+c,a-c＜b-c.
性质3：不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
如果a＞b,且c＞0,那么ac＞bc, a÷c＞b÷c.
如果a＞b,且c＜0,那么ac＜bc, a÷c＜b÷c.
做一做：　　我国于2001年12月11日正式加入世界贸易组织（WTO）。加入前，产品A的进口税超过产品B的进口税的1倍以上；加入后，这两种产品的进口税都下调了15%。你认为加入后产品A的进口税仍超过产品B的进口税的1倍以上吗？请说明理由。　 解　设加入前产品A，B的进口税分别为a美元,b美元。由题意,得,a>2b。加入后A，B两种产品的进口税分别为（1-15%）a，（1-15%）b，由不等式的基本性质3，
∵　1-15%＞0
∴（1-15%）a＞2 （1-15%）b
即表示产品A的进口税仍超过产品B的进口税的1倍以上。变式与思考1：1、若a=0，比较a与2a的大小4、若a=－3，比较a与2a的大小a＞2a2、若a=3，比较a与2a的大小3、若a＞0，比较a与2a的大小
a=2aa＜2aa＜2a1、若a＜b，b＜2a－1，则a______2a－14、 若a ＜b，则2－a_____2－b3、若－a＜b，则a_______ －b选择恰当的不等号填空，并说出理由。2、若a＞－b，则a+b______0＞＞＞＜变式与思考2：例 已知a＜0，试比较2a与a的大小. 解法一：∵2a－a＝a
又∵a＜0
∴2a－a＜0
∴2a＜a（不等式基本性质2）以上比较大小的方法叫作差法,你知道这一方法的基本原理吗?解法二:
解法三:
在数轴上分别表示2a和a的点(a＜0)2a位于a的左边，所以2a＜a例4：某品牌计算机键盘的单价在60元至70元之间，买3个这样的键盘需要多少钱？（用适当的不等式表示） 解：(1)根据不等式基本性质1，两边都加上2，
得： x-2+2＜3+2
x＜5
(2)根据不等式基本性质1，两边都减去5x，
得： 6x-5x＜5x-1-5x
x＜-1四、典型例题：
例1.根据不等式的基本性质，把下列不等式化成x＜a或x＞a的形式：
(1) x-2＜ 3 (2) 6x＜ 5x-1
(3) 1/2 x＞5 (4) -4x＞3 例2.设a＞b，用“＜”或“＞”填空：
(1)a-3 b-3 (2) (3) -4a -4b解：(1) ∵a＞b
∴两边都减去3，由不等式基本性质1
得 a-3＞b-3
(2) ∵a＞b，并且2＞0
∴两边都除以2，由不等式基本性质2
得 (3) ∵a＞b，并且-4＜0
∴两边都乘以-4，由不等式基本性质3
得 -4a＜-4b五、变式训练：
1、已知x＜y,用“＜”或“＞”填空。
（1）x+2 y+2 （不等式的基本性质 ）
(2) x y （不等式的基本性质 ）
（3）－x －y （不等式的基本性质 ）
(4)x－m y－m （不等式的基本性质 ） 　　　　　　　　　　　　　　　2、若a-b<0，则下列各式中一定成立
的是（ ）
A.a>b B.ab>0
C. D.-a>-b
3、若x是任意实数，则下列不等式中，
恒成立的是（ ）
A.3x>2x B.3x2>2x2
C.3+x>2 D.3+x2>2DD BDCD 5、判断正误：
(1)∵a+8＞4 (2)∵3＞2
∴a＞-4 ( ) ∴3a＞2a( )
(3)∵-1＞-2 (4)∵ab＞0
∴a-1＞a-2 ( ) ∴a＞0,b＞ 0( )√×√×6、下列各题是否正确?请说明理由(1)如果a＞b,那么ac＞bc(2)如果a＞b,那么ac2 ＞bc2
(3)如果ac2＞bc2,那么a＞b(4)如果a＞b,那么a-b＞0(5)如果ax＞b且a≠0,那么x＞b/a7、利用不等式的基本性质填空，
（填“＜”或“＞”）
（1）若a＞b，则2a+1 2b+1，
（2）若－ y＜10，则y －8，
（3）若a＜b，且c＞0，则
ac+c bc+ c，
（4）若a＞0，b＜0，c＜0，则
（a－b）c 0。8、试一试：(1) 2a和a+1(2)2a和a-1比较2a与a的大小(1)当a>0时，2a>a；
(2)当a=0时，2a=a；
(3)当a<0时，2a(a-3)y，
求a的取值范围.解：∵x(a-3)y，∴a-3<0（不等式的基本性质3）∴a<3（不等式的基本性质2）提高题： ＞＞＞＜＜＜不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1