2.3有理数乘法课件

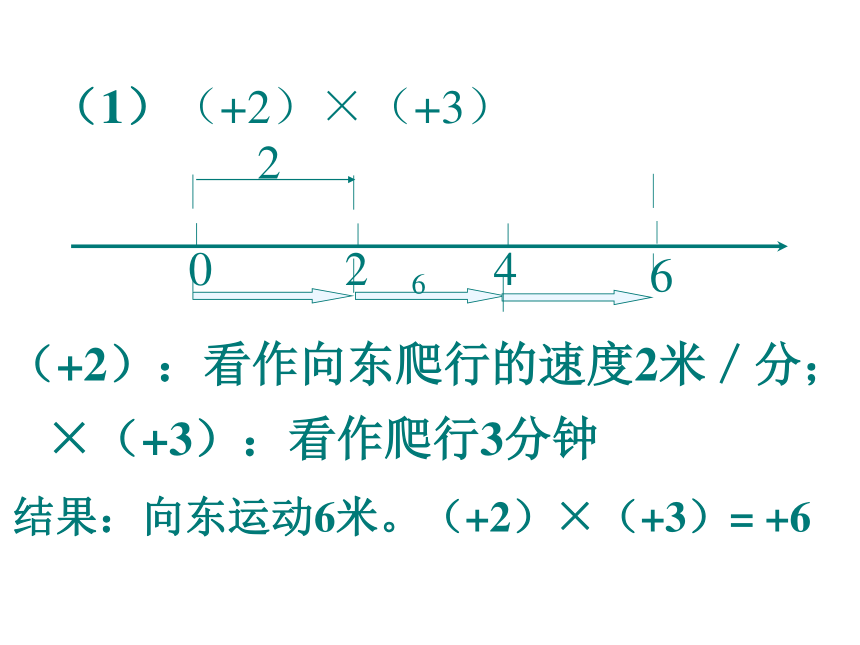
课件22张PPT。耳到、眼到、口到、心到七年级 数学（上）自主、合作、探究、互动2.3、有理数的乘法（1）第2章 有理数的运算合作学习：一只乌龟在东西向的一条直线上爬行，并且爬行的速度是每分钟２米，规定向东为正，在Ａ点的时候的时刻为零．情景假设：A（1）（+2）×（+3）（+2）：看作向东爬行的速度2米／分；×（+3）：看作爬行3分钟　结果：向东运动6米。（+2）×（+3）= +6(2).（-2）×（+3）×（ + 3）：看作爬行3分钟结果：向西运动6米。 （-2）×（+3）＝-6（－2）：看作向西爬行的速度2米／分；(3). （+2）×（-3）讨论１：（+2）：看作向东爬行的速度2米／分；×（-3）：表示三分钟之前(4) (-2) ×(-3)讨论２：（-2）：看作向西爬行的速度2米／分；×（-3）：表示三分钟之前（5） 0 × 5 =0在原地爬行5次（-5）×0 =0向西方爬行0次结果：被乘数是0或者乘数是0，
结果仍在原处。 0 × 0 = 05个例子综合如下：
（1） 2×3=6
（2）（-2）×3= -6
（3） 2×（-3）= -6
（4）（-2）×（-3）=6
（5） 被乘数或乘数为0时，结果是0 有理数乘法法则
两数相乘，同号得正，异号得负，并把绝对值相乘。任何数同0相乘，都得0。正正得正，负负得正，异号得负练习1：确定下列积的符号：
（１）　 5×（-3）　
（２）　（-4）×6
（３）　（-7）×（-9）
（４）　　0.5×0.7积的符号为负
积的符号为负
积的符号为正
积的符号为正
?

?
例１:运算步骤再确定积的符号；后进行绝对值的乘法运算先判断类型
（同号、异号等）；练习２：
（-6）×0.25
(-0.5)×(-8)　　
×( )
(４)(-0.3)×( )　
(５)　 × 25思考：观察下列各式，它们的积是正的还是负的？
（1）（-1） ×2 ×3 ×4
（2） （-1） ×（-2 ）×3 ×4
（3） （-1） ×（-2 ）×（-3 ）×4
（4） （-1） ×（-2 ）×（-3 ）×（-4）
（5） （-1） ×（-2 ）×（-3 ）×（-4）×0 几个有理数相乘，因数都不为0时，积的符号由负因数的个数决定。当有奇数个负因数时积为负；当有偶数个负因数时积为正；当有一个因数为零时，积是零。结论：计算：①
②
③
④
⑤
⑥练习３：例 题 解 析例2 计算：
(1) (2)


(3)
求解中的第一步是 确定积的符号 第二步
是 绝对值相乘倒 数 的 定 义 由例 1 的 (1) (3)的求解:? 解题后的反思 ? 可知 乘积为 1 的两个有理数称为互为倒数.的为乘积为 1，例3、求下列各数的倒数： （1） - 3 （2）- 1 （3 ） （4） 0．2 （5） 1．2注意（1）0没有倒数。
（2）求分数的倒数，只要把这个分数的分子，分母颠倒位置即可。
（3）正数的倒数是正数，负数的倒数是负数。(4)求小数的倒数时，要先把小数化成分数；
(5)求带分数的倒数时，要先把带分数化成假分数。小结：1.有理数乘法法则：两数相乘,同号得正,异好号得负,并把绝对值相乘,任何数同0相乘,都得0。2.如何进行两个有理数的运算：先确定积的符号，再把绝对值相乘，当有一个因数为零时，积为零。