3.2三角形的内切圆复习
图片预览


文档简介
课件17张PPT。3.2 三角形的内切圆 1、定义:和三角形各边都相切的圆叫做三角形的内切圆,
内切圆的圆心叫做三角形的内心,这个三角形叫做圆的
外切三角形。回顾旧知2、性质: 内心到三角形三边的距离相等;
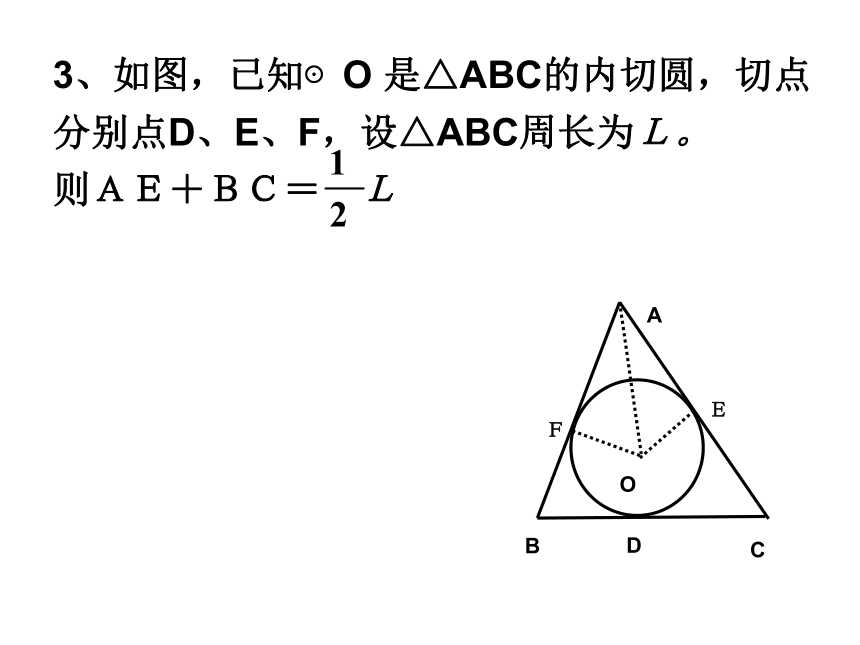
内心与顶点连线平分内角。3、如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
则AE+BC= LOABCFEDABCOcDEr如:直角三角形的两直角边分别是6cm,8cm 则其内切圆的半径为______。 变式
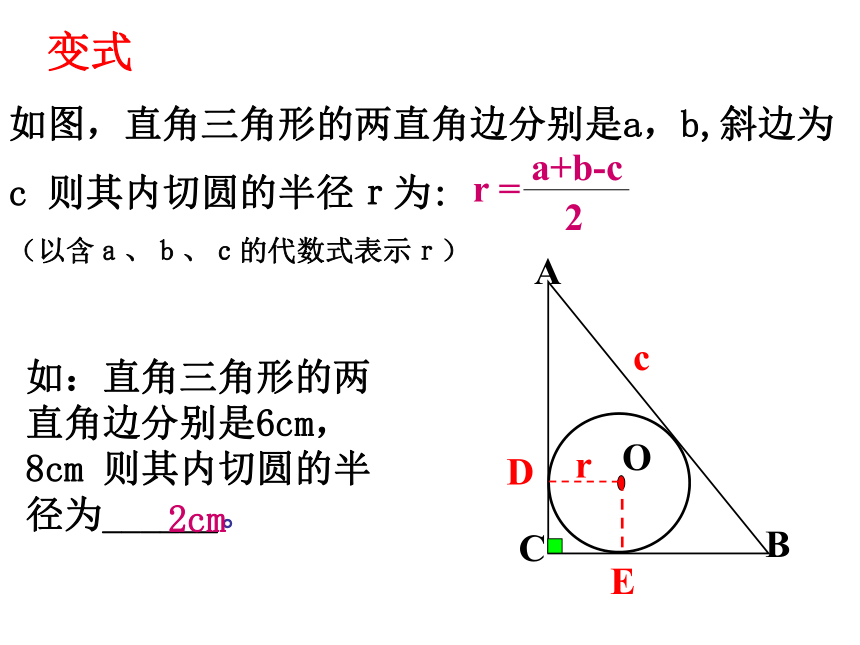
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cm学以致用 课内练习
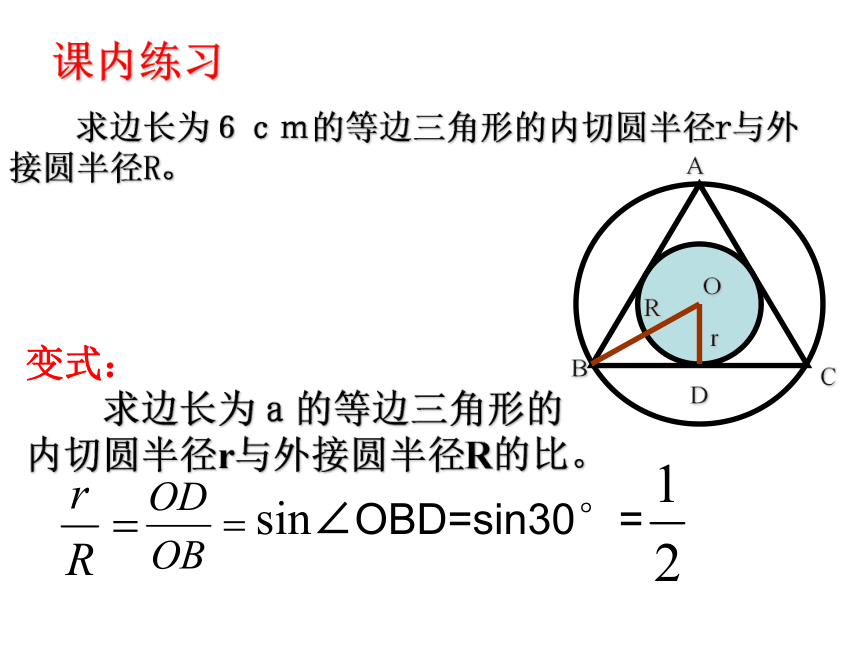
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。变式:
求边长为a的等边三角形的
内切圆半径r与外接圆半径R的比。sin∠OBD=sin30°=
课内练习
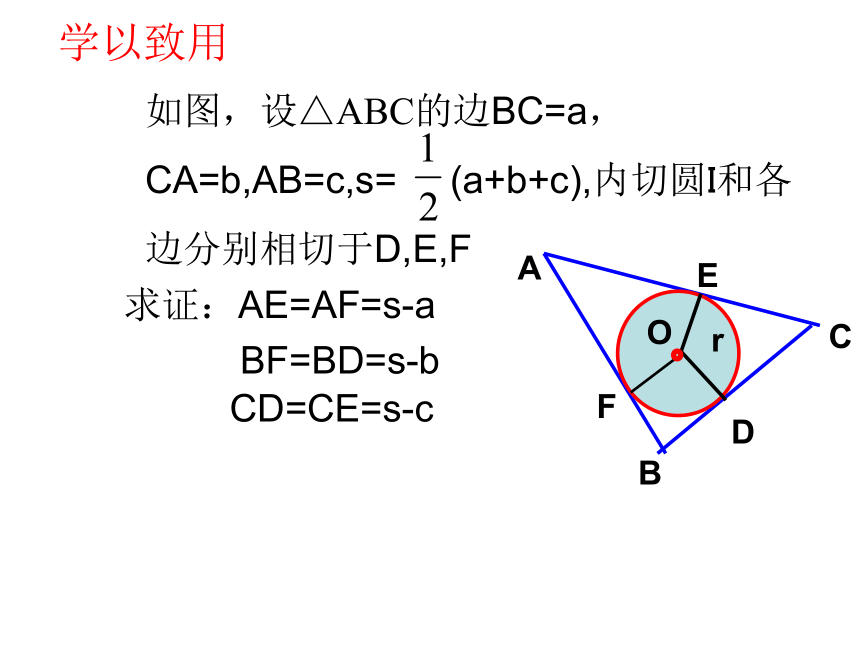
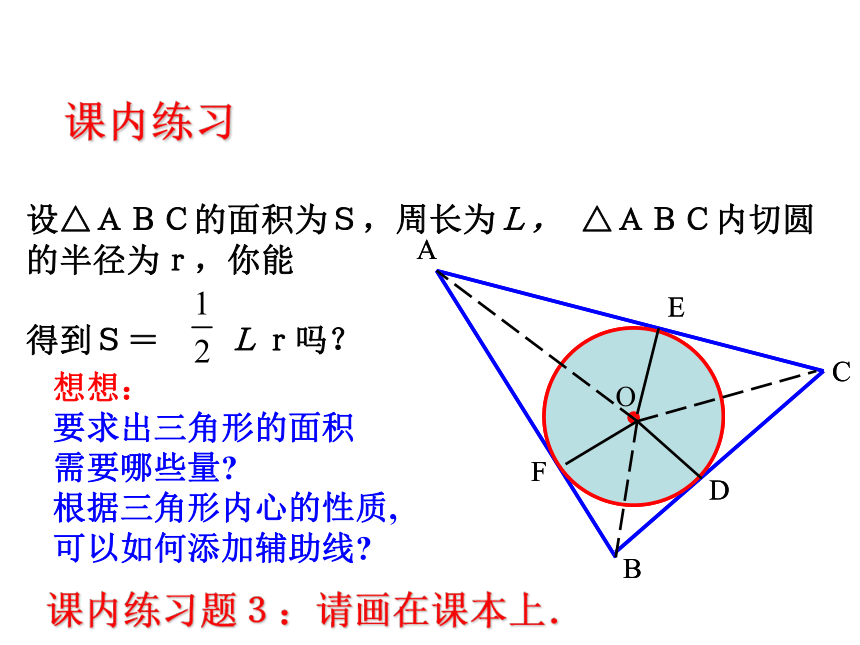
设△ABC的面积为S,周长为L, △ABC内切圆
的半径为r,你能
得到S= Lr吗?想想:
要求出三角形的面积
需要哪些量?
根据三角形内心的性质,
可以如何添加辅助线?课内练习题3:请画在课本上.
以某三角形的内心为圆心,作一个圆使它与这个三角形的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI探究活动1. ) 三角形的内心到三角形各个顶点的距离相等( )
2. ) 三角形的外心到三角形各边的距离相等 ( )
3. ) 等边三角形的内心和外心重合; ( )
4. ) 三角形的内心一定在三角形的内部( )
5. ) 菱形一定有内切圆( )
6. ) 矩形一定有内切圆( )错错对对 错 对1、判断题:快乐抢答(2)如图,如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB= (3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )APABD快乐抢答11691.如图1,⊙O内切于△ABC,切点为D,E,F.
已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,
那么∠EDF等于( )
A.40° B.55° C.65° D.70°
图1 图2 图3
2.如图2,⊙O是△ABC的内切圆,D,E,F是切点,
∠A=50°,∠C=60°,则∠DOE=( )
A.70° B.110° C.120° D.130°
3.如图3,△ABC中,∠A=45°,I是内心,
则∠BIC=( )
A.112.5° B.112° C.125° D.55°必答题BBA如图,△ABC中,∠A=m°
(1)如图(1),当O是△ABC的内心时,
求∠BOC的度数;
(2)如图(2),当O是△ABC的外心时,
求∠BOC的度数;
(3)如图(3),当O是高线BD与CE的交点时,
求∠BOC的度数.
变式4.下列命题正确的是( )
A.三角形的内心到三角形三个顶点的距离相等
B.三角形的内心不一定在三角形的内部
C.等边三角形的内心,外心重合
D.一个圆一定有唯一一个外切三角形
5.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的
内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5必答题CC6.如图,在△ABC中,AB=AC,内切圆O与边BC,
AC,AB分别切于D,E,F.
(1)求证:BF=CE;
(2)若∠C=30°,CE=2,求AC的长.
笔答题7.如图,在半径为R的圆内作一个内接正方形,然后
作这个正方形的内切圆,又在这个内切圆中作内接
正方形,依此作到第n个内切圆,它的半径是( )A.(B.()nR)n-1R)nRC.()n-1RD.(思考题8.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长
线交BC于点D,AC=4,DC=1,则⊙O的半径等于( )
A. B. C. D.9.如图,已知正三角形ABC的边长为2a.
(1)求它的内切圆与外接圆组成的圆环的面积;
(2)根据计算结果,要求圆环的面积,只需测量
哪一条弦的大小就可算出圆环的面积;
(3)将条件中的“正三角形”改为“正方形”“正六边形”,
你能得出怎样的结论?
(4)已知正n边形的边长为2a,请写出它的内切圆与
外接圆组成的圆环面积.拓展提高 10. 如图,⊙O与四边形ABCD的各边依次切于M,N,
G,H.
(1)猜想AB+CD与AD+BC有何数量关系,并证明你的
猜想;
(2)若四边形ABCD增加条件AD∥BC而成为梯形,
梯形的中位线长为m,其他条件不变,试用m表示
梯形的周长.
内切圆的圆心叫做三角形的内心,这个三角形叫做圆的
外切三角形。回顾旧知2、性质: 内心到三角形三边的距离相等;
内心与顶点连线平分内角。3、如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
则AE+BC= LOABCFEDABCOcDEr如:直角三角形的两直角边分别是6cm,8cm 则其内切圆的半径为______。 变式
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cm学以致用 课内练习
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。变式:
求边长为a的等边三角形的
内切圆半径r与外接圆半径R的比。sin∠OBD=sin30°=
课内练习
设△ABC的面积为S,周长为L, △ABC内切圆
的半径为r,你能
得到S= Lr吗?想想:
要求出三角形的面积
需要哪些量?
根据三角形内心的性质,
可以如何添加辅助线?课内练习题3:请画在课本上.
以某三角形的内心为圆心,作一个圆使它与这个三角形的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI探究活动1. ) 三角形的内心到三角形各个顶点的距离相等( )
2. ) 三角形的外心到三角形各边的距离相等 ( )
3. ) 等边三角形的内心和外心重合; ( )
4. ) 三角形的内心一定在三角形的内部( )
5. ) 菱形一定有内切圆( )
6. ) 矩形一定有内切圆( )错错对对 错 对1、判断题:快乐抢答(2)如图,如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB= (3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )APABD快乐抢答11691.如图1,⊙O内切于△ABC,切点为D,E,F.
已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,
那么∠EDF等于( )
A.40° B.55° C.65° D.70°
图1 图2 图3
2.如图2,⊙O是△ABC的内切圆,D,E,F是切点,
∠A=50°,∠C=60°,则∠DOE=( )
A.70° B.110° C.120° D.130°
3.如图3,△ABC中,∠A=45°,I是内心,
则∠BIC=( )
A.112.5° B.112° C.125° D.55°必答题BBA如图,△ABC中,∠A=m°
(1)如图(1),当O是△ABC的内心时,
求∠BOC的度数;
(2)如图(2),当O是△ABC的外心时,
求∠BOC的度数;
(3)如图(3),当O是高线BD与CE的交点时,
求∠BOC的度数.
变式4.下列命题正确的是( )
A.三角形的内心到三角形三个顶点的距离相等
B.三角形的内心不一定在三角形的内部
C.等边三角形的内心,外心重合
D.一个圆一定有唯一一个外切三角形
5.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的
内切圆与外接圆半径分别为( )
A.1.5,2.5 B.2,5 C.1,2.5 D.2,2.5必答题CC6.如图,在△ABC中,AB=AC,内切圆O与边BC,
AC,AB分别切于D,E,F.
(1)求证:BF=CE;
(2)若∠C=30°,CE=2,求AC的长.
笔答题7.如图,在半径为R的圆内作一个内接正方形,然后
作这个正方形的内切圆,又在这个内切圆中作内接
正方形,依此作到第n个内切圆,它的半径是( )A.(B.()nR)n-1R)nRC.()n-1RD.(思考题8.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长
线交BC于点D,AC=4,DC=1,则⊙O的半径等于( )
A. B. C. D.9.如图,已知正三角形ABC的边长为2a.
(1)求它的内切圆与外接圆组成的圆环的面积;
(2)根据计算结果,要求圆环的面积,只需测量
哪一条弦的大小就可算出圆环的面积;
(3)将条件中的“正三角形”改为“正方形”“正六边形”,
你能得出怎样的结论?
(4)已知正n边形的边长为2a,请写出它的内切圆与
外接圆组成的圆环面积.拓展提高 10. 如图,⊙O与四边形ABCD的各边依次切于M,N,
G,H.
(1)猜想AB+CD与AD+BC有何数量关系,并证明你的
猜想;
(2)若四边形ABCD增加条件AD∥BC而成为梯形,
梯形的中位线长为m,其他条件不变,试用m表示
梯形的周长.
