特殊的平行四边形

(共16张PPT)
引领者：
矩形基本知识回顾
说一说
1、矩形的性质（按边、角、对角线分类）
⑴边：对边平行且相等，邻边互相垂直。
⑵角：四个角都是直角。
⑶对角线：两条对角线互相平分且相等。
辨一辨
2、判断下列命题的真假：
⑴有一个角是直角的平行四边形是矩形。　（　　）
⑵对角线相等的四边形是矩形。　　　　　（　　）
⑶有三个角都是直角的四边形是矩形。　　（　　）
⑷对角线互相平分且相等的四边形是矩形。（　　）
真
真
假
真
矩形基本知识回顾
智力大冲浪
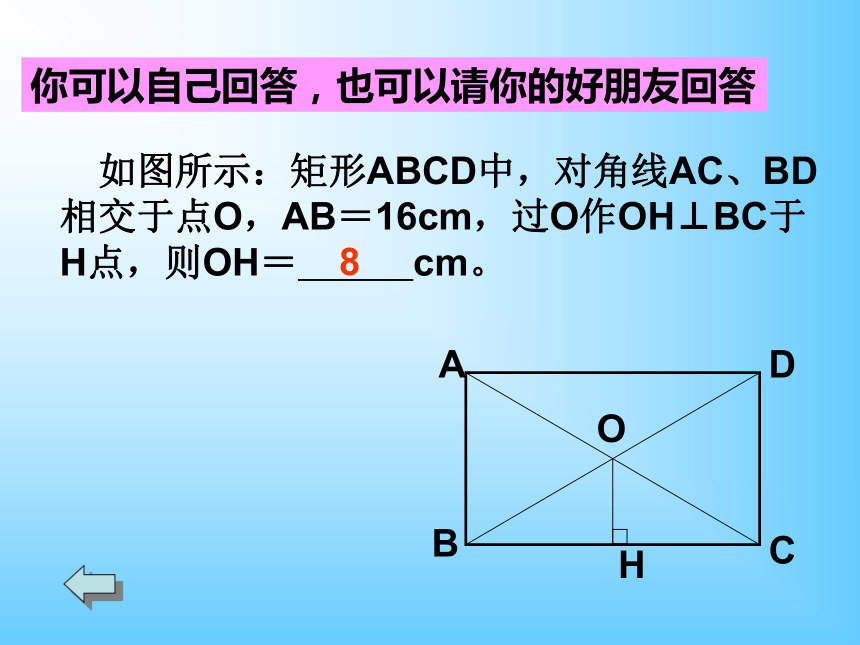
　如图所示：矩形ABCD中，对角线AC、BD
相交于点O，AB＝16cm，过O作OH⊥BC于
H点，则OH＝　　　cm。
A
B
D
C
O
H
8
你可以自己回答，也可以请你的好朋友回答
请你自己回答
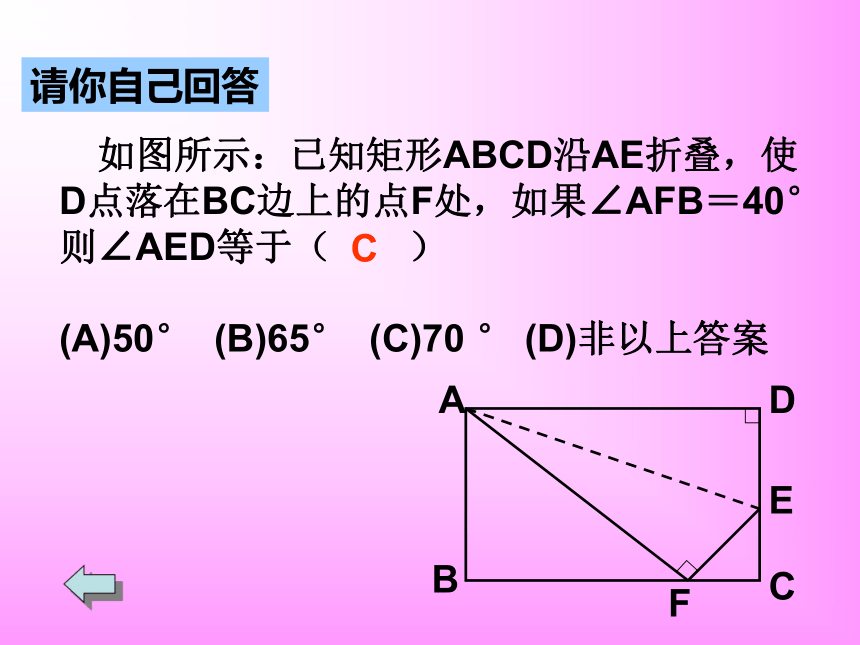
　如图所示：已知矩形ABCD沿AE折叠，使
D点落在BC边上的点F处，如果∠AFB＝40°
则∠AED等于（　　）
(A)50° (B)65° (C)70 ° (D)非以上答案
C
A
B
D
C
E
F
例1：利用矩形的性质证明：“直角三角形斜边
上的中线等于斜边的一半”。
小结：证明　　　　型问题，可采用“加长法”
或“折半法”加以解决。
学一学
如图，在Rt△ABC中，∠ACB＝90°
CM是AB上的中线
A
C
B
M
E
已知：
求证：
∵
∴
　1：如图：在Rt△ABC中，CD是斜边AB
上的中线，已知∠DCA＝25°，则
∠A＝　　　　， ∠B＝　　　　。
A
C
B
D
25°
65°
练一练
　2： 一张平行四边形纸片（如图），现要求剪一刀，把它分成两部分，然后作适当的图形变换，把剪开的两部分拼成一个矩形，说明你的剪法和所采用的变换。
动一动
例2：如图，已知矩形ABCD中，延长BC至E，使BE＝BD，
F为DE中点，连结AF、CF，求证：AF⊥CF
在△BDE中
BD＝BE，DF＝EF
BF⊥DE（三线合一）
∠1+∠2＝90°
要证： AF⊥CF
∠1+∠3＝90°
∠2＝∠3
△ADF≌△BCF
∠ADF＝∠BCF
CF＝DF
AD＝BC
CF是Rt△DCE的中线
矩形ABCD
CF＝DF
∠CDF＝∠DCF
∠ADC＝∠BCD＝90°
分析思路图：
　3： 如图，在△ABC中，点O是AC边上一个动点，过点O的直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。
⑴求证：EO＝FO
⑵当点O运动到何处时，四边形AECF是矩形？证明你的结论。
想一想
小　结
2、求证线段倍分的问题，常常可以采用“加长法”或“折半法”，或利用“三角形的中位线”等性质加以解决。
3、解决较复杂的几何图形问题，常常可以考虑：把原图形分解成几个基本图形，达到降低难度、勾通已知与结论的联系的目的。
4、“两头凑”思路是解决较复杂证明题的行之有效的分析方法。
直角三角形斜边上的中线等于斜边的一半。　　
利用这个定理，可以形成等腰三角形，解决一些角相等、线段倍分的问题。
1、直角三角形的性质定理：
A
C
B
M
2、书本P138—139，第1—4题
3、八年级（下）《数学作业本（2）》P35，§6.1 矩形（3）
作业（必做）
做一做
作业（选做）
4、书本P139　　第5题
5、思考提高题：
　 设矩形ABCD，AB＝6，AD＝10，现沿对角线BD折叠（如图），求AE的长。
A
B
C
D
E
C’
做一做
条理清晰，因果相应，言必有据
是初学证明者谨记和遵循的原则
结束寄语