4.6 图形的位似
图片预览


文档简介
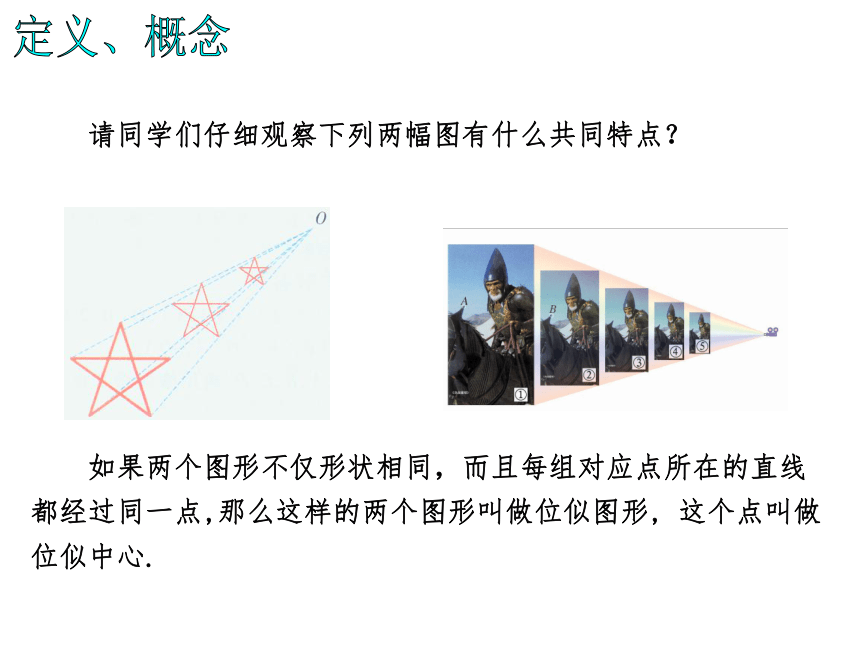
课件16张PPT。浙教版初中数学九年级(上) 4.6 图形的位似引导者:王曙明请同学们仔细观察下列两幅图有什么共同特点? 如果两个图形不仅形状相同,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形, 这个点叫做位似中心.定义、概念明晰新知
1.两图形相似. 同时满足下面两个条件的两个图形才叫
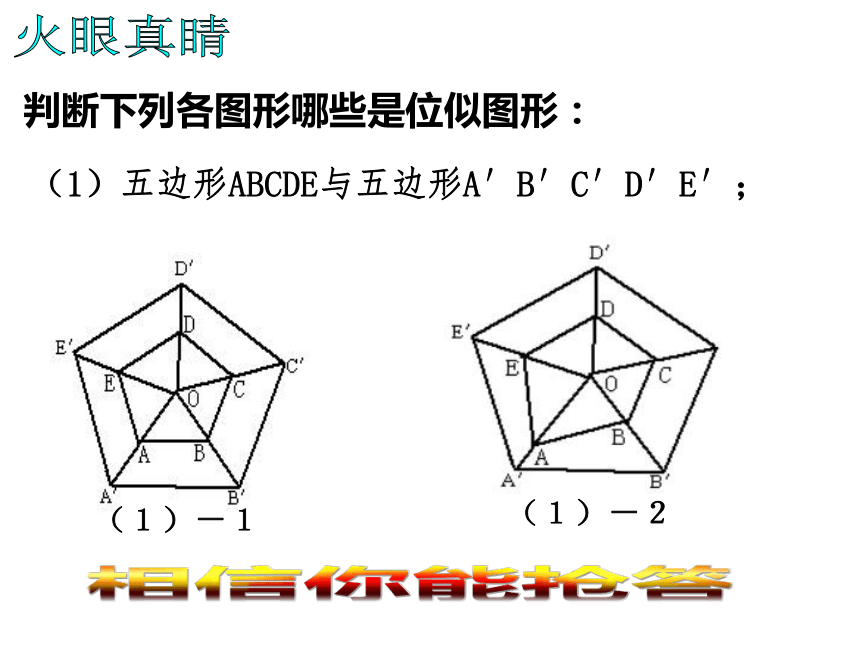
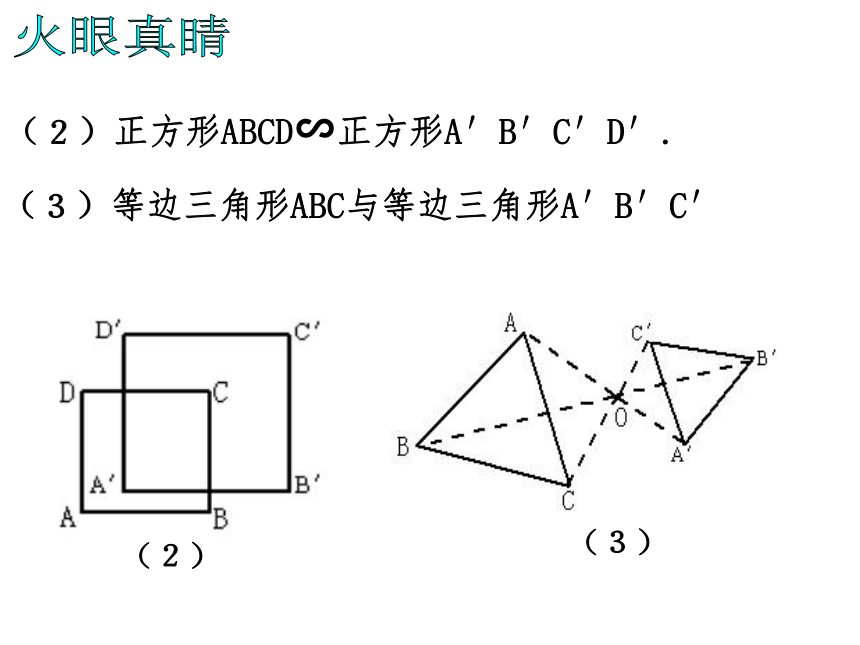
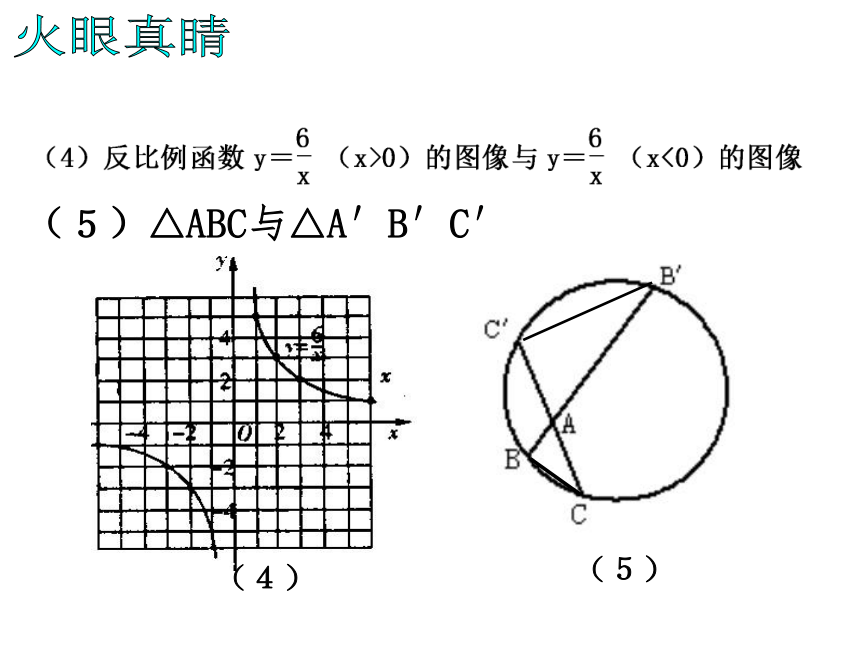
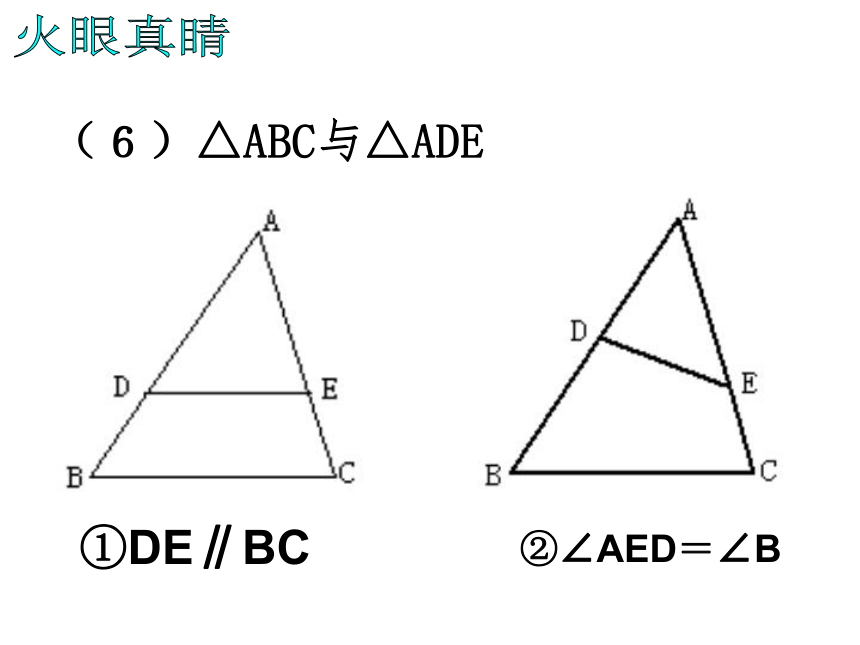
做位似图形.两条件缺一不可. 显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比. 2.每组对应点所在直线都经过同一点. 火眼真睛判断下列各图形哪些是位似图形: (1)五边形ABCDE与五边形A′B′C′D′E′; 相信你能抢答(1)-1(1)-2(2)正方形ABCD∽正方形A′B′C′D′. (3)等边三角形ABC与等边三角形A′B′C′(2)(3)火眼真睛(5)△ABC与△A′B′C′ (4)(5)火眼真睛(6)△ABC与△ADE ①DE∥BC②∠AED=∠B火眼真睛 2.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比. 基础练习观察与思考 下列位似图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你能猜想对应点到位似中心的距离之比与位似比之间有什么关系? 位似图形性质的探索一般地,位似图形有以下性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比. 例.如图,请以坐标原点O为位似中心,作平行四边形ABCD的位似图形,并把它的边长放大2倍. 分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和的各顶点,并把线段延长(或反向延长)到原来的2倍,就得到所求作图形的各个顶点 以坐标原点为位似中心的位似变换有一下性质:
若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky).
思有所得小试牛刀 如图:在直角坐标系中, △ABC的各个顶点的坐标A(-1,1)B(2,3)C(0,3) 现要以坐标原点O为位似中心,像与原图形的位似比为2,作△ABC的位似图形△A`B`C`,则它的顶点A`、B`、C`的坐标各是多少? 1、下列说法正确的是( )A、将图形A平移后得到图形B,则它们是位似图形B、将图形A绕某点旋转180°后得到图形B,则它们是位似图形C、两个关于某直线成轴对称的图形一定是位似图形D、全等的两个图形一定是位似图形试试伸手试试伸手 2、如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半. 1、如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点, 那么这样的两个图形叫做 。
2、 这个点叫做 。
3、这时的相似比又称为 。
4、位似图形上任意一对对应点到位似中心的距离之比等于 。
5、在以坐标原点为位似中心的位似变换中若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为
。
6、我学会了把任意图形 。位似图形位似中心位似比位似比放大与缩小课堂小结(kx,ky)或(―kx,―ky)
做位似图形.两条件缺一不可. 显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比. 2.每组对应点所在直线都经过同一点. 火眼真睛判断下列各图形哪些是位似图形: (1)五边形ABCDE与五边形A′B′C′D′E′; 相信你能抢答(1)-1(1)-2(2)正方形ABCD∽正方形A′B′C′D′. (3)等边三角形ABC与等边三角形A′B′C′(2)(3)火眼真睛(5)△ABC与△A′B′C′ (4)(5)火眼真睛(6)△ABC与△ADE ①DE∥BC②∠AED=∠B火眼真睛 2.如图P,E,F分别是AC,AB,AD的中点,四边形AEPF与四边形ABCD是位似图形吗?如果是位似图形,说出位似中心和位似比. 基础练习观察与思考 下列位似图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你能猜想对应点到位似中心的距离之比与位似比之间有什么关系? 位似图形性质的探索一般地,位似图形有以下性质:
位似图形上任意一对对应点到位似中心的距离之比等于位似比. 例.如图,请以坐标原点O为位似中心,作平行四边形ABCD的位似图形,并把它的边长放大2倍. 分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心O和的各顶点,并把线段延长(或反向延长)到原来的2倍,就得到所求作图形的各个顶点 以坐标原点为位似中心的位似变换有一下性质:
若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为(kx,ky)或(―kx,―ky).
思有所得小试牛刀 如图:在直角坐标系中, △ABC的各个顶点的坐标A(-1,1)B(2,3)C(0,3) 现要以坐标原点O为位似中心,像与原图形的位似比为2,作△ABC的位似图形△A`B`C`,则它的顶点A`、B`、C`的坐标各是多少? 1、下列说法正确的是( )A、将图形A平移后得到图形B,则它们是位似图形B、将图形A绕某点旋转180°后得到图形B,则它们是位似图形C、两个关于某直线成轴对称的图形一定是位似图形D、全等的两个图形一定是位似图形试试伸手试试伸手 2、如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长缩小到原来的一半. 1、如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点, 那么这样的两个图形叫做 。
2、 这个点叫做 。
3、这时的相似比又称为 。
4、位似图形上任意一对对应点到位似中心的距离之比等于 。
5、在以坐标原点为位似中心的位似变换中若原图形上点的坐标为(x,y),像与原图形的位似比为k,则像上的对应点的坐标为
。
6、我学会了把任意图形 。位似图形位似中心位似比位似比放大与缩小课堂小结(kx,ky)或(―kx,―ky)
同课章节目录
