圆与圆的位置关系复习课件
图片预览


文档简介
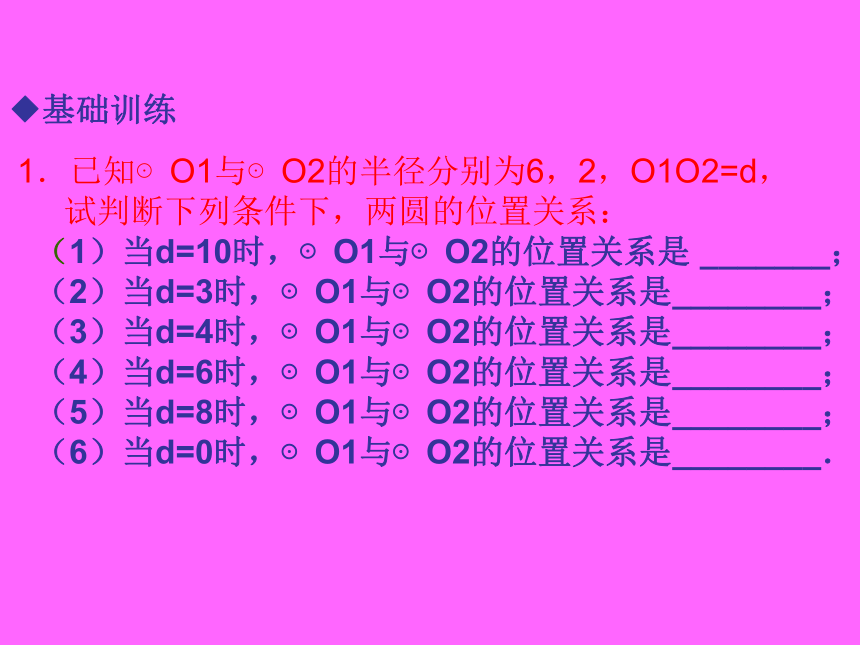
课件17张PPT。圆与圆的位置关系复习◆基础训练1.已知⊙O1与⊙O2的半径分别为6,2,O1O2=d,
试判断下列条件下,两圆的位置关系:
(1)当d=10时,⊙O1与⊙O2的位置关系是 _______;
(2)当d=3时,⊙O1与⊙O2的位置关系是________;
(3)当d=4时,⊙O1与⊙O2的位置关系是________;
(4)当d=6时,⊙O1与⊙O2的位置关系是________;
(5)当d=8时,⊙O1与⊙O2的位置关系是________;
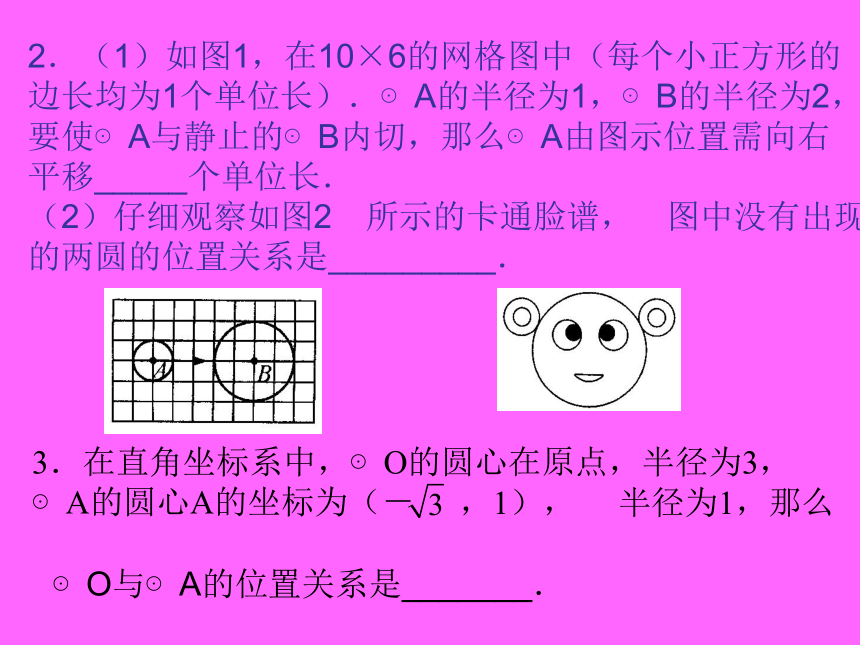
(6)当d=0时,⊙O1与⊙O2的位置关系是________.2.(1)如图1,在10×6的网格图中(每个小正方形的
边长均为1个单位长).⊙A的半径为1,⊙B的半径为2,
要使⊙A与静止的⊙B内切,那么⊙A由图示位置需向右
平移_____个单位长.
(2)仔细观察如图2所示的卡通脸谱,图中没有出现
的两圆的位置关系是_________.
3.在直角坐标系中,⊙O的圆心在原点,半径为3,
⊙A的圆心A的坐标为(-,1), 半径为1,那么
⊙O与⊙A的位置关系是_______.4.如图3,两圆轮叠靠在墙边,已知两轮半径分别为4
和1,则它们与墙的切点A,B间的距离为________.
5.如图4,矩形ABCD中,AB=18,AD=25,去掉一个
与三边相切的⊙M后,余下部分能剪出的最大圆的直
径是( )
A.8 B.7 C.6 D.4
6.如图是某城市一个主题雕塑的平面示意图,它由置
放于地面L上两个半径为2米的半圆与半径为4米的⊙A
构成,点B,C分别是两个半圆的圆心,⊙A分别与两
个半圆相切于点E,F,BC长为8米,求EF的长.
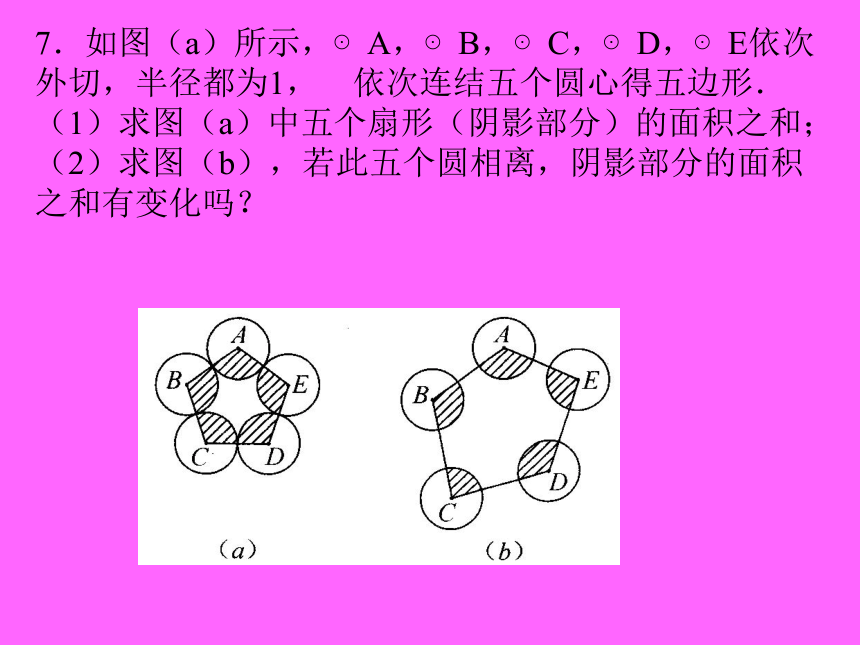
7.如图(a)所示,⊙A,⊙B,⊙C,⊙D,⊙E依次
外切,半径都为1,依次连结五个圆心得五边形.
(1)求图(a)中五个扇形(阴影部分)的面积之和;
(2)求图(b),若此五个圆相离,阴影部分的面积
之和有变化吗?
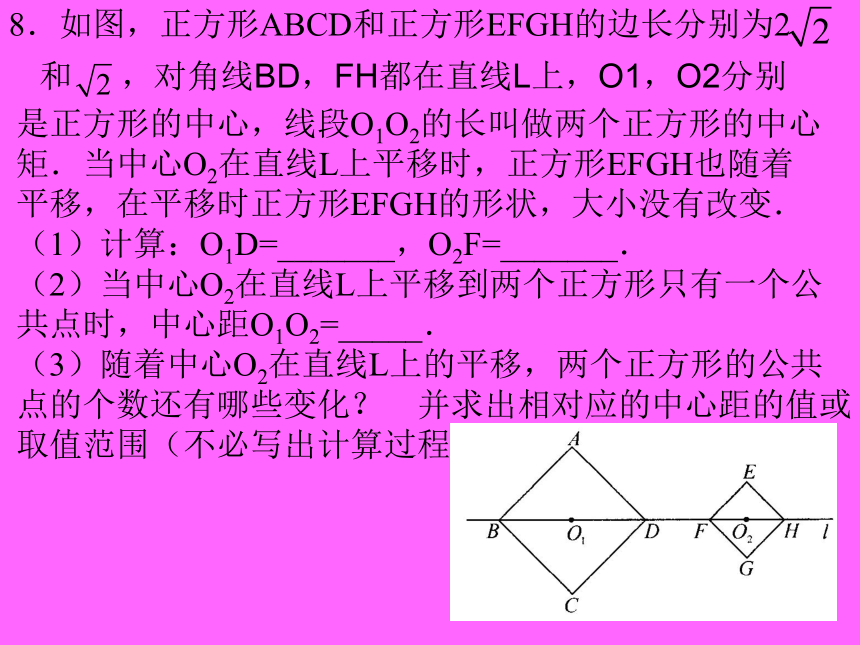
8.如图,正方形ABCD和正方形EFGH的边长分别为2和是正方形的中心,线段O1O2的长叫做两个正方形的中心
矩.当中心O2在直线L上平移时,正方形EFGH也随着
平移,在平移时正方形EFGH的形状,大小没有改变.
(1)计算:O1D=_______,O2F=_______.
(2)当中心O2在直线L上平移到两个正方形只有一个公
共点时,中心距O1O2=_____.
(3)随着中心O2在直线L上的平移,两个正方形的公共
点的个数还有哪些变化?并求出相对应的中心距的值或
取值范围(不必写出计算过程).,对角线BD,FH都在直线L上,O1,O2分别◆提高训练
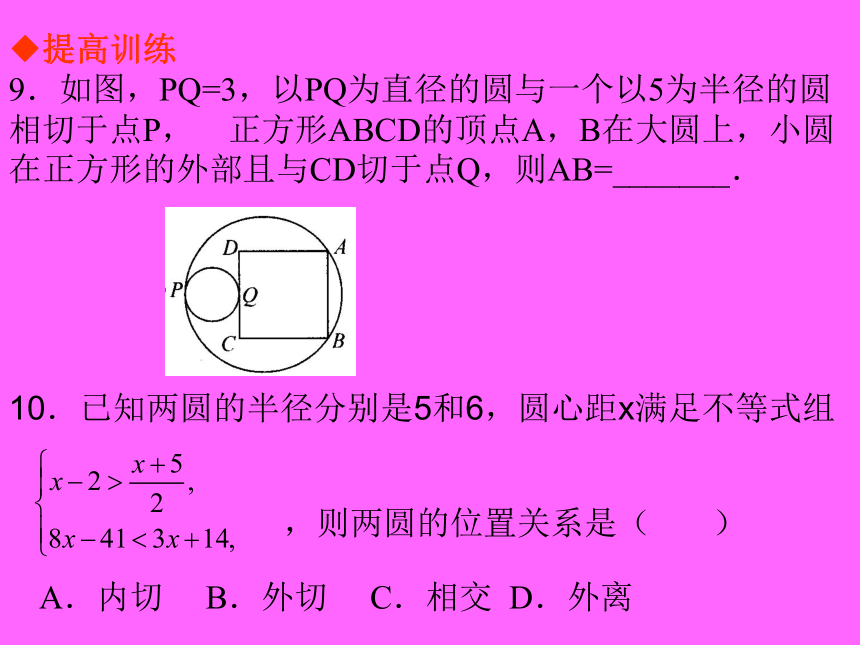
9.如图,PQ=3,以PQ为直径的圆与一个以5为半径的圆
相切于点P,正方形ABCD的顶点A,B在大圆上,小圆
在正方形的外部且与CD切于点Q,则AB=_______.A.内切 B.外切 C.相交 D.外离,则两圆的位置关系是( )10.已知两圆的半径分别是5和6,圆心距x满足不等式组11.已知:AB为⊙O的直径,P为(1)若⊙O′与⊙O外切于点P(如图甲),AP,BP
的延长线分别交⊙O′于点C,D,连接CD,则△PCD
是_______三角形;
(2)若⊙O′与⊙O相交于点P,Q(如图乙),连接
AQ,BQ并延长分别交⊙O′于点E,F,请选择下列
两个问题中的一个作答:
问题一:判断△PEF的形状,并证明你的结论;
问题二:判断线段AE与BF的关系,并证明你的结论.
我选择问题_______,结论:________.的中点,如图3-3-12所示.12.如图,△ABC中,∠BAC的平分线交BC于D,交
△ABC的外接圆⊙O1于E,过点C,D,E作⊙O2,
AC的延长线交⊙O2于F.
(1)求证:EF2=ED·EA;
(2)若AE=6,EF=3,求AF·AC的值.13.如图,已知⊙O1与⊙O2交于A,B,⊙O1的半径为17,
⊙O2的半径为10,O1O2=21,求AB的长.
14.如图,已知⊙O1与⊙O2交于A,B两点,过A的直线
交两圆于C,D两点,G为CD的中点,BG及其延长线
交⊙O1,⊙O2于E,F,连结DF,CE,求证:CE=DF.
◆拓展训练
15.如图所示,已知⊙O1与⊙O2外切,它们的半径分别
是1和3,那么半径为4且和⊙O1,⊙O2都相切的圆共
有( )
A.1个 B.2个 C.5个 D.6个16.设边长为2a的正方形的中心A在直线L上,它的一组对边垂直于直线L,半 径为r的⊙O的圆心O在直线L上 (1)如图3-3-17①,当r将⊙O与正方形的公共点个数填入下表:
所以,当r=a时,⊙O与正方形的公共点个数可能有______个.
(3)如图3-3-17③,当⊙O与正方形有5个公共点时,试说明r=a;
(4)就r>a的情形,请你仿照“当……时,⊙O与正方形的公共点个数可能有_____个”的形式,至少给出一个关于“⊙O与正方形的公共点个数”的正确结论.运动,点A,O间距离为d.
所以,当r_______个.2)如图3-3-17②,当r=a时,根据d与a,r之间关系,
将⊙O与正方形的公共点个数填入下表:所以,当r=a时,⊙O与正方形的公共点个数可能有
______个.(3)如图3-3-17③,当⊙O与正方形有5个公共点时,
试说明r=;
(4)就r>a的情形,请你仿照“当……时,⊙O与
正方形的公共点个数可能有_____个”的形式,至少给出
一个关于“⊙O与正方形的公共点个数”的正确结论.a再见!再见祝同学们学习进步!
试判断下列条件下,两圆的位置关系:
(1)当d=10时,⊙O1与⊙O2的位置关系是 _______;
(2)当d=3时,⊙O1与⊙O2的位置关系是________;
(3)当d=4时,⊙O1与⊙O2的位置关系是________;
(4)当d=6时,⊙O1与⊙O2的位置关系是________;
(5)当d=8时,⊙O1与⊙O2的位置关系是________;
(6)当d=0时,⊙O1与⊙O2的位置关系是________.2.(1)如图1,在10×6的网格图中(每个小正方形的
边长均为1个单位长).⊙A的半径为1,⊙B的半径为2,
要使⊙A与静止的⊙B内切,那么⊙A由图示位置需向右
平移_____个单位长.
(2)仔细观察如图2所示的卡通脸谱,图中没有出现
的两圆的位置关系是_________.
3.在直角坐标系中,⊙O的圆心在原点,半径为3,
⊙A的圆心A的坐标为(-,1), 半径为1,那么
⊙O与⊙A的位置关系是_______.4.如图3,两圆轮叠靠在墙边,已知两轮半径分别为4
和1,则它们与墙的切点A,B间的距离为________.
5.如图4,矩形ABCD中,AB=18,AD=25,去掉一个
与三边相切的⊙M后,余下部分能剪出的最大圆的直
径是( )
A.8 B.7 C.6 D.4
6.如图是某城市一个主题雕塑的平面示意图,它由置
放于地面L上两个半径为2米的半圆与半径为4米的⊙A
构成,点B,C分别是两个半圆的圆心,⊙A分别与两
个半圆相切于点E,F,BC长为8米,求EF的长.
7.如图(a)所示,⊙A,⊙B,⊙C,⊙D,⊙E依次
外切,半径都为1,依次连结五个圆心得五边形.
(1)求图(a)中五个扇形(阴影部分)的面积之和;
(2)求图(b),若此五个圆相离,阴影部分的面积
之和有变化吗?
8.如图,正方形ABCD和正方形EFGH的边长分别为2和是正方形的中心,线段O1O2的长叫做两个正方形的中心
矩.当中心O2在直线L上平移时,正方形EFGH也随着
平移,在平移时正方形EFGH的形状,大小没有改变.
(1)计算:O1D=_______,O2F=_______.
(2)当中心O2在直线L上平移到两个正方形只有一个公
共点时,中心距O1O2=_____.
(3)随着中心O2在直线L上的平移,两个正方形的公共
点的个数还有哪些变化?并求出相对应的中心距的值或
取值范围(不必写出计算过程).,对角线BD,FH都在直线L上,O1,O2分别◆提高训练
9.如图,PQ=3,以PQ为直径的圆与一个以5为半径的圆
相切于点P,正方形ABCD的顶点A,B在大圆上,小圆
在正方形的外部且与CD切于点Q,则AB=_______.A.内切 B.外切 C.相交 D.外离,则两圆的位置关系是( )10.已知两圆的半径分别是5和6,圆心距x满足不等式组11.已知:AB为⊙O的直径,P为(1)若⊙O′与⊙O外切于点P(如图甲),AP,BP
的延长线分别交⊙O′于点C,D,连接CD,则△PCD
是_______三角形;
(2)若⊙O′与⊙O相交于点P,Q(如图乙),连接
AQ,BQ并延长分别交⊙O′于点E,F,请选择下列
两个问题中的一个作答:
问题一:判断△PEF的形状,并证明你的结论;
问题二:判断线段AE与BF的关系,并证明你的结论.
我选择问题_______,结论:________.的中点,如图3-3-12所示.12.如图,△ABC中,∠BAC的平分线交BC于D,交
△ABC的外接圆⊙O1于E,过点C,D,E作⊙O2,
AC的延长线交⊙O2于F.
(1)求证:EF2=ED·EA;
(2)若AE=6,EF=3,求AF·AC的值.13.如图,已知⊙O1与⊙O2交于A,B,⊙O1的半径为17,
⊙O2的半径为10,O1O2=21,求AB的长.
14.如图,已知⊙O1与⊙O2交于A,B两点,过A的直线
交两圆于C,D两点,G为CD的中点,BG及其延长线
交⊙O1,⊙O2于E,F,连结DF,CE,求证:CE=DF.
◆拓展训练
15.如图所示,已知⊙O1与⊙O2外切,它们的半径分别
是1和3,那么半径为4且和⊙O1,⊙O2都相切的圆共
有( )
A.1个 B.2个 C.5个 D.6个16.设边长为2a的正方形的中心A在直线L上,它的一组对边垂直于直线L,半 径为r的⊙O的圆心O在直线L上 (1)如图3-3-17①,当r
所以,当r=a时,⊙O与正方形的公共点个数可能有______个.
(3)如图3-3-17③,当⊙O与正方形有5个公共点时,试说明r=a;
(4)就r>a的情形,请你仿照“当……时,⊙O与正方形的公共点个数可能有_____个”的形式,至少给出一个关于“⊙O与正方形的公共点个数”的正确结论.运动,点A,O间距离为d.
所以,当r
将⊙O与正方形的公共点个数填入下表:所以,当r=a时,⊙O与正方形的公共点个数可能有
______个.(3)如图3-3-17③,当⊙O与正方形有5个公共点时,
试说明r=;
(4)就r>a的情形,请你仿照“当……时,⊙O与
正方形的公共点个数可能有_____个”的形式,至少给出
一个关于“⊙O与正方形的公共点个数”的正确结论.a再见!再见祝同学们学习进步!
