二次函数的图象与性质(A卷)
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
二次函数的图象与性质(A卷)
姓名: 分数:
一、选择题:(每题2分,共30分)
1.抛物线y=x2+3x的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.抛物线y=-3x2+2x-1的图象与x轴、y轴交点的个数是( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
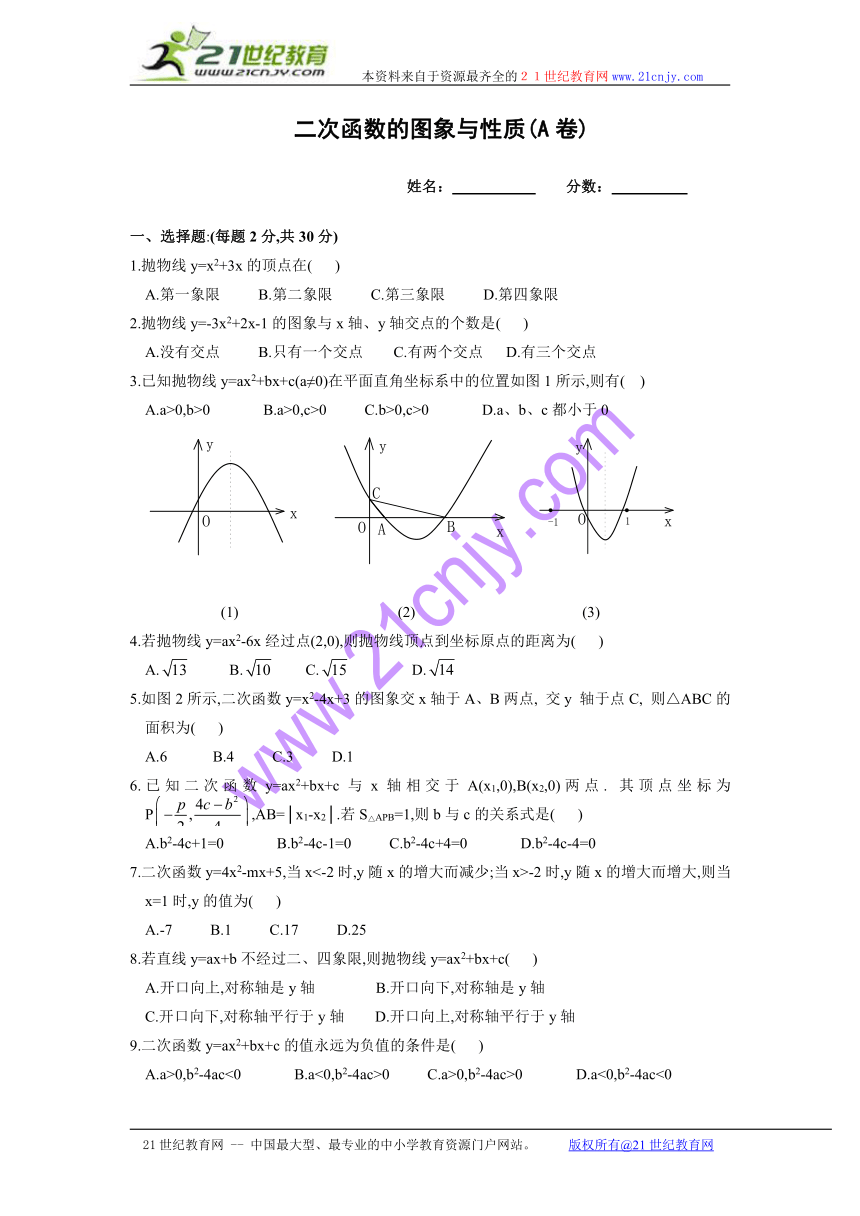
3.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图1所示,则有( )
A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a、b、c都小于0
(1) (2) (3)
4.若抛物线y=ax2-6x经过点(2,0),则抛物线顶点到坐标原点的距离为( )
A. B. C. D.
5.如图2所示,二次函数y=x2-4x+3的图象交x轴于A、B两点, 交y 轴于点C, 则△ABC的面积为( )
A.6 B.4 C.3 D.1
6.已知二次函数y=ax2+bx+c与x轴相交于A(x1,0),B(x2,0)两点. 其顶点坐标为P,AB=│x1-x2│.若S△APB=1,则b与c的关系式是( )
A.b2-4c+1=0 B.b2-4c-1=0 C.b2-4c+4=0 D.b2-4c-4=0
7.二次函数y=4x2-mx+5,当x<-2时,y随x的增大而减少;当x>-2时,y随x的增大而增大,则当x=1时,y的值为( )
A.-7 B.1 C.17 D.25
8.若直线y=ax+b不经过二、四象限,则抛物线y=ax2+bx+c( )
A.开口向上,对称轴是y轴 B.开口向下,对称轴是y轴
C.开口向下,对称轴平行于y轴 D.开口向上,对称轴平行于y轴
9.二次函数y=ax2+bx+c的值永远为负值的条件是( )
A.a>0,b2-4ac<0 B.a<0,b2-4ac>0 C.a>0,b2-4ac>0 D.a<0,b2-4ac<0
10.二次函数y=ax2+bx+c的图象如图3所示,那么abc,b2-4ac,2a+b,a+b+c 这四个代数式中,值为正数的有( )
A.4个 B.3个 C.2个 D.1个
11.已知二次函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象可能是图所示的( )
12.已知抛物线y=5x2+(m-1)x+m与x轴的两个交点在y轴同侧,它们的距离平方等于,则m的值为( )
A.-2 B.12 C.24 D.48
13.函数y=x2+px+q的图象是以(3,2)为顶点的抛物线,则这个函数的关系式是( )
A.y=x2+6x+11 B.y=x2-6x-11 C.y=x2-6x+11 D.y=x2-6x+7
14.关于函数y=2x2-8x,下列叙述中错误的是( )
A.函数图象经过原点 B.函数图象的最低点是(2,-8)
C.函数图象与x轴的交点为(0,0),(4,0) D.函数图象的对称轴是直线x=-2
15.如图所示,当b<0时,函数y=ax+b与y=ax2+bx+c在同一坐标系内的图象可能是( )
二、填空题:(每题3分,共45分)
16.二次函数y=2x2- 4x+ 3 通过配方化为顶点式为y= _________, 其对称轴是______,顶点坐标为_______,抛物线开口________,当x_______时,y随x 的增大而增大;当x____时,y随x的增大而减小;当x=______时,y最值=________.
17.已知抛物线y=x2+(m-1)x-的顶点的横坐标是2,则m的值是_______.
18.已知抛物线的对称轴是x=-1,它与x轴交点间的距离等于4,它在y轴上的截距是-6,则它的关系式是_____________.
19.若二次函数y=ax2+bx+c的图象经过点(0,-1),(5,-1), 则它的对称轴方程是________.
20.在同一坐标系内,抛物线y=ax2与直线y=2x+b相交于A、B两点,若点A 的坐标是(2,4),则点B的坐标是_________.
21.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为__________.
22.若二次函数y=(m+5)x2+2(m+1)x+m的图象全部在x轴的上方,则m 的取值范围是_____.
23.已知抛物线y=ax2+bx+c(a≠0)图象的顶点为P(-2,3),且过A(-3,0), 则抛物线的关系式为___________.
24.当n=________,m=______时,函数y=(m+n)+(m-n)x的图象是抛物线,且其顶点在原点,此抛物线的开口________.
25.若抛物线y=ax2+bx+c经过(0,1)和(2,-3)两点,且开口向下,对称轴在y 轴左侧,则a的取值范围是_________.
26.已知函数y=x2-1840x+2003与x轴的交点为(m,0),(n,0),
则(m2-1841m+2003)(n2-1841n+2003)的值为______.
27.已知抛物线y=x2+bx+c与y轴交于点A,与x轴的正半轴交于B、C两点,且BC=2,S△ABC=3.那么b=________.
28.直线y=x+2与抛物线y=x2+2x的交点坐标为________.
29.如图所示,A、B、C是二次函数y=ax2+bx+c(a≠0)的图象上的三点,根据图中给出的三点位置情况,可得a、c 、 △( △= b2- 4ac) 与零的大小关系是
a_____0,c____0,△_____0,(填入“>”、“<”或“=”)
30.有一个二次函数的图象,三位学生分别说出了它的一些特点:甲:对称轴是直线x=4;乙:与x轴的两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3,请你写出满足上述全部特点的一个二次函数关系式___________.
三、解答题:(25分)
31.(6分)(1)请你画出函数y=x2-4x+10的图象, 由图象你能发现这个函数具有哪些性质
(2)通过配方变形,说出函数y=-2x2+8x-8的图象的开口方向、对称轴、 顶点坐标,这个函数有最大值还是最小值 这个值是多少
32.(6分)根据下列条件,分别求出对应的二次函数关系式.
(1)已知抛物线的顶点是(-1,-2),且过点(1,10);
(2)已知抛物线过三点:(0,-2),(1,0),(2,3).
33.(6分)已知二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数.
(1)求证:不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)设这个二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1、x2的倒数和为,求这个二次函数的关系式.
34.(7分)某商场购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20 元的价格销售时, 每月能卖300件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的前提下,问销售价格定为多少时,才能使每月获得最大利润 每月的最大利润是多少 (总利润=总收入-总成本)
答案:
一、1.C 2.B 3.C 4.B 5.C 6.D 7.D 8.A 9.D 10.A 11.A 12. C 13.C 14.D 15.B
二、16.2(x-1)2+1;直线x=1;(1,1);向上;x>1;x<1;1;1
17.-3 18.y=2x2+4x-6 19.x= 20.(0,0) 21.y=-4x2+16x-13
22.m> 23.y=-3x2-12x-9 24.2;2 25.-128.(1,3),(-2,0) 29.<;<;> 30.y=
三、
31.解:(1)函数图象如答图所示,性质有:
①该函数图象的开口向上,对称轴为直线x=4,顶点(4,2).
②当x>4时,y随x的增大而增大;
当x<4时,y随x 的增大而减小.
③当x=4时,y最小值=2.
(2)y=-2x2+8x-8=-2(x-2)2.
该函数图象的开口向下,对称轴为直线x=2,顶点(2,0);
∵a=-2<0,
∴y有最大值,当x=2时,y最大值=0.
32.解:(1)∵抛物线顶点(-1,-2),
∴设所求二次函数关系式为y=a(x+1)2-2,
把(1,10)代入上式,得10=a(1+1)2-2.
∴a=3,∴y=3(x+1)2-2,即y=3x2+6x+1.
(2)设所求二次函数关系为y=ax2+bx+c,
把(0,-2),(1,0),(2,3)分别代入y=ax2+bx+c,得
,
∴
33.(1)证明:∵△=b2-4ac=[-2(m-1)]2-4(m2-2m-3)=4m2-8m+4-4m2+8m+12=16> 0,
∴无论m为何值,此二次函数图象与x轴必有两个交点.
(2)解:x1,x2是方程x2-2(m-1)x+m2-2m-3=0的两根,
则有x1+x2=2(m-1) , x1x2=m2-2m-3.
∵,∴,∴,
∴3m-3=m2-2m-3,m2-5m=0.解得m=0或m=5.
所求二次函数关系式为y=x2+2x-3或y=x2-8x+12.
34.解:(1)设y与x的函数关系式为y=kx+b,
把x=20,y=300;x=25,y=210 分别代入y=kx+b,
得,k=-18,b=660.
∴y=-18x+660,16≤x≤.
(2)获得利润m=(x-16)·y=(x-16)(-18x+660)
=-18x2+948x-10560=-18 +1922.
∵a=-18<0,∴当x=时,m最大值=1922(元).
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
二次函数的图象与性质(A卷)
姓名: 分数:
一、选择题:(每题2分,共30分)
1.抛物线y=x2+3x的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.抛物线y=-3x2+2x-1的图象与x轴、y轴交点的个数是( )
A.没有交点 B.只有一个交点 C.有两个交点 D.有三个交点
3.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图1所示,则有( )
A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a、b、c都小于0
(1) (2) (3)
4.若抛物线y=ax2-6x经过点(2,0),则抛物线顶点到坐标原点的距离为( )
A. B. C. D.
5.如图2所示,二次函数y=x2-4x+3的图象交x轴于A、B两点, 交y 轴于点C, 则△ABC的面积为( )
A.6 B.4 C.3 D.1
6.已知二次函数y=ax2+bx+c与x轴相交于A(x1,0),B(x2,0)两点. 其顶点坐标为P,AB=│x1-x2│.若S△APB=1,则b与c的关系式是( )
A.b2-4c+1=0 B.b2-4c-1=0 C.b2-4c+4=0 D.b2-4c-4=0
7.二次函数y=4x2-mx+5,当x<-2时,y随x的增大而减少;当x>-2时,y随x的增大而增大,则当x=1时,y的值为( )
A.-7 B.1 C.17 D.25
8.若直线y=ax+b不经过二、四象限,则抛物线y=ax2+bx+c( )
A.开口向上,对称轴是y轴 B.开口向下,对称轴是y轴
C.开口向下,对称轴平行于y轴 D.开口向上,对称轴平行于y轴
9.二次函数y=ax2+bx+c的值永远为负值的条件是( )
A.a>0,b2-4ac<0 B.a<0,b2-4ac>0 C.a>0,b2-4ac>0 D.a<0,b2-4ac<0
10.二次函数y=ax2+bx+c的图象如图3所示,那么abc,b2-4ac,2a+b,a+b+c 这四个代数式中,值为正数的有( )
A.4个 B.3个 C.2个 D.1个
11.已知二次函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象可能是图所示的( )
12.已知抛物线y=5x2+(m-1)x+m与x轴的两个交点在y轴同侧,它们的距离平方等于,则m的值为( )
A.-2 B.12 C.24 D.48
13.函数y=x2+px+q的图象是以(3,2)为顶点的抛物线,则这个函数的关系式是( )
A.y=x2+6x+11 B.y=x2-6x-11 C.y=x2-6x+11 D.y=x2-6x+7
14.关于函数y=2x2-8x,下列叙述中错误的是( )
A.函数图象经过原点 B.函数图象的最低点是(2,-8)
C.函数图象与x轴的交点为(0,0),(4,0) D.函数图象的对称轴是直线x=-2
15.如图所示,当b<0时,函数y=ax+b与y=ax2+bx+c在同一坐标系内的图象可能是( )
二、填空题:(每题3分,共45分)
16.二次函数y=2x2- 4x+ 3 通过配方化为顶点式为y= _________, 其对称轴是______,顶点坐标为_______,抛物线开口________,当x_______时,y随x 的增大而增大;当x____时,y随x的增大而减小;当x=______时,y最值=________.
17.已知抛物线y=x2+(m-1)x-的顶点的横坐标是2,则m的值是_______.
18.已知抛物线的对称轴是x=-1,它与x轴交点间的距离等于4,它在y轴上的截距是-6,则它的关系式是_____________.
19.若二次函数y=ax2+bx+c的图象经过点(0,-1),(5,-1), 则它的对称轴方程是________.
20.在同一坐标系内,抛物线y=ax2与直线y=2x+b相交于A、B两点,若点A 的坐标是(2,4),则点B的坐标是_________.
21.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为__________.
22.若二次函数y=(m+5)x2+2(m+1)x+m的图象全部在x轴的上方,则m 的取值范围是_____.
23.已知抛物线y=ax2+bx+c(a≠0)图象的顶点为P(-2,3),且过A(-3,0), 则抛物线的关系式为___________.
24.当n=________,m=______时,函数y=(m+n)+(m-n)x的图象是抛物线,且其顶点在原点,此抛物线的开口________.
25.若抛物线y=ax2+bx+c经过(0,1)和(2,-3)两点,且开口向下,对称轴在y 轴左侧,则a的取值范围是_________.
26.已知函数y=x2-1840x+2003与x轴的交点为(m,0),(n,0),
则(m2-1841m+2003)(n2-1841n+2003)的值为______.
27.已知抛物线y=x2+bx+c与y轴交于点A,与x轴的正半轴交于B、C两点,且BC=2,S△ABC=3.那么b=________.
28.直线y=x+2与抛物线y=x2+2x的交点坐标为________.
29.如图所示,A、B、C是二次函数y=ax2+bx+c(a≠0)的图象上的三点,根据图中给出的三点位置情况,可得a、c 、 △( △= b2- 4ac) 与零的大小关系是
a_____0,c____0,△_____0,(填入“>”、“<”或“=”)
30.有一个二次函数的图象,三位学生分别说出了它的一些特点:甲:对称轴是直线x=4;乙:与x轴的两个交点的横坐标都是整数;丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3,请你写出满足上述全部特点的一个二次函数关系式___________.
三、解答题:(25分)
31.(6分)(1)请你画出函数y=x2-4x+10的图象, 由图象你能发现这个函数具有哪些性质
(2)通过配方变形,说出函数y=-2x2+8x-8的图象的开口方向、对称轴、 顶点坐标,这个函数有最大值还是最小值 这个值是多少
32.(6分)根据下列条件,分别求出对应的二次函数关系式.
(1)已知抛物线的顶点是(-1,-2),且过点(1,10);
(2)已知抛物线过三点:(0,-2),(1,0),(2,3).
33.(6分)已知二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数.
(1)求证:不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)设这个二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1、x2的倒数和为,求这个二次函数的关系式.
34.(7分)某商场购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20 元的价格销售时, 每月能卖300件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的前提下,问销售价格定为多少时,才能使每月获得最大利润 每月的最大利润是多少 (总利润=总收入-总成本)
答案:
一、1.C 2.B 3.C 4.B 5.C 6.D 7.D 8.A 9.D 10.A 11.A 12. C 13.C 14.D 15.B
二、16.2(x-1)2+1;直线x=1;(1,1);向上;x>1;x<1;1;1
17.-3 18.y=2x2+4x-6 19.x= 20.(0,0) 21.y=-4x2+16x-13
22.m> 23.y=-3x2-12x-9 24.2;2 25.-1
三、
31.解:(1)函数图象如答图所示,性质有:
①该函数图象的开口向上,对称轴为直线x=4,顶点(4,2).
②当x>4时,y随x的增大而增大;
当x<4时,y随x 的增大而减小.
③当x=4时,y最小值=2.
(2)y=-2x2+8x-8=-2(x-2)2.
该函数图象的开口向下,对称轴为直线x=2,顶点(2,0);
∵a=-2<0,
∴y有最大值,当x=2时,y最大值=0.
32.解:(1)∵抛物线顶点(-1,-2),
∴设所求二次函数关系式为y=a(x+1)2-2,
把(1,10)代入上式,得10=a(1+1)2-2.
∴a=3,∴y=3(x+1)2-2,即y=3x2+6x+1.
(2)设所求二次函数关系为y=ax2+bx+c,
把(0,-2),(1,0),(2,3)分别代入y=ax2+bx+c,得
,
∴
33.(1)证明:∵△=b2-4ac=[-2(m-1)]2-4(m2-2m-3)=4m2-8m+4-4m2+8m+12=16> 0,
∴无论m为何值,此二次函数图象与x轴必有两个交点.
(2)解:x1,x2是方程x2-2(m-1)x+m2-2m-3=0的两根,
则有x1+x2=2(m-1) , x1x2=m2-2m-3.
∵,∴,∴,
∴3m-3=m2-2m-3,m2-5m=0.解得m=0或m=5.
所求二次函数关系式为y=x2+2x-3或y=x2-8x+12.
34.解:(1)设y与x的函数关系式为y=kx+b,
把x=20,y=300;x=25,y=210 分别代入y=kx+b,
得,k=-18,b=660.
∴y=-18x+660,16≤x≤.
(2)获得利润m=(x-16)·y=(x-16)(-18x+660)
=-18x2+948x-10560=-18 +1922.
∵a=-18<0,∴当x=时,m最大值=1922(元).
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
