浙教版2024学年八年级下册数学第二章《一元二次方程》提高卷(含答案)
文档属性
| 名称 | 浙教版2024学年八年级下册数学第二章《一元二次方程》提高卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 844.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024学年八年级下册数学第二章《一元二次方程》提高卷(附答案)
选择题(本题共10小题,每小题3分,共30分)
已知关于的方程是一元二次方程,则的取值范围是( )
B. C. D.
方程的解是( )
B. C. 或 D. 或
一元二次方程的根的情况是( )
有两个不相等的实数根 B. 有两个相等的实数根
C . 没有实数根 D. 无法确定
用配方法解方程,方程应变形为( )
B. C. D.
某银行经过两次降息,使一年存款的年利率由原来的2.25%降低至1.21%,设平均每次降息的百分率为,则满足方程( )
B.
C . D.
已知,(为任意实数),则的大小关系为( )
B. M已知一个直角三角形的 两边长是方程的两个根,则此直角三角形的第三边的长为( )
6或8 B. 8或10 C. 10或 D.
设是方程的两个根,则的值为( )
7 B. 8 C. 9 D. 10
如图所示,某市世纪广场有一块长为18、宽为15的长方形绿地,在绿地中开辟三条道路后,剩余绿地的面积为182,则的值为( )
2 B. 22 C. 2或22 D. 4或22
若方程x2+2(1+a)x+3a2+4ab+4b2+2=0有实数根,则=( )
B. - C. D.
填空题(本题共6小题,每小题3分,共18分)
若关于的一元二次方程有两个相等的实数根,则= .
若为实数,且,则= .
设是一元二次方程的两个根,则的值为 .
若关于的一元二次方程中,,,满足和则=
.
如图,在△ABC中,∠B=,AB=9cm,BC=12cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过秒,使得△PBQ的面积为18.则= .
如图,直线OB是一次函数的图象,点A的坐标为(0,2),在直线OB上找点C,使得ΔACO是以OA为腰的等腰三角形,则点C的坐标为 .
解答题:(本大题有 7小题,共52分)
17(本题8分). 选用适当的方法解下列一元二次方程:
(2)
18(本题5分). 已知关于的一元二次方程有一个根是3,求的值.
19(本题7分). 已知关于的一元二次方程.
求证:无论取什么实数,方程总有实数根.
若等腰△ABC的一边长,另两边长恰好是这个方程的两个根,求△ABC的周长.
20(本题7分). 已知关于的一元二次方程有实数根.
求的取值范围.
当时,设原方程的两个实数根为,且,求的值.
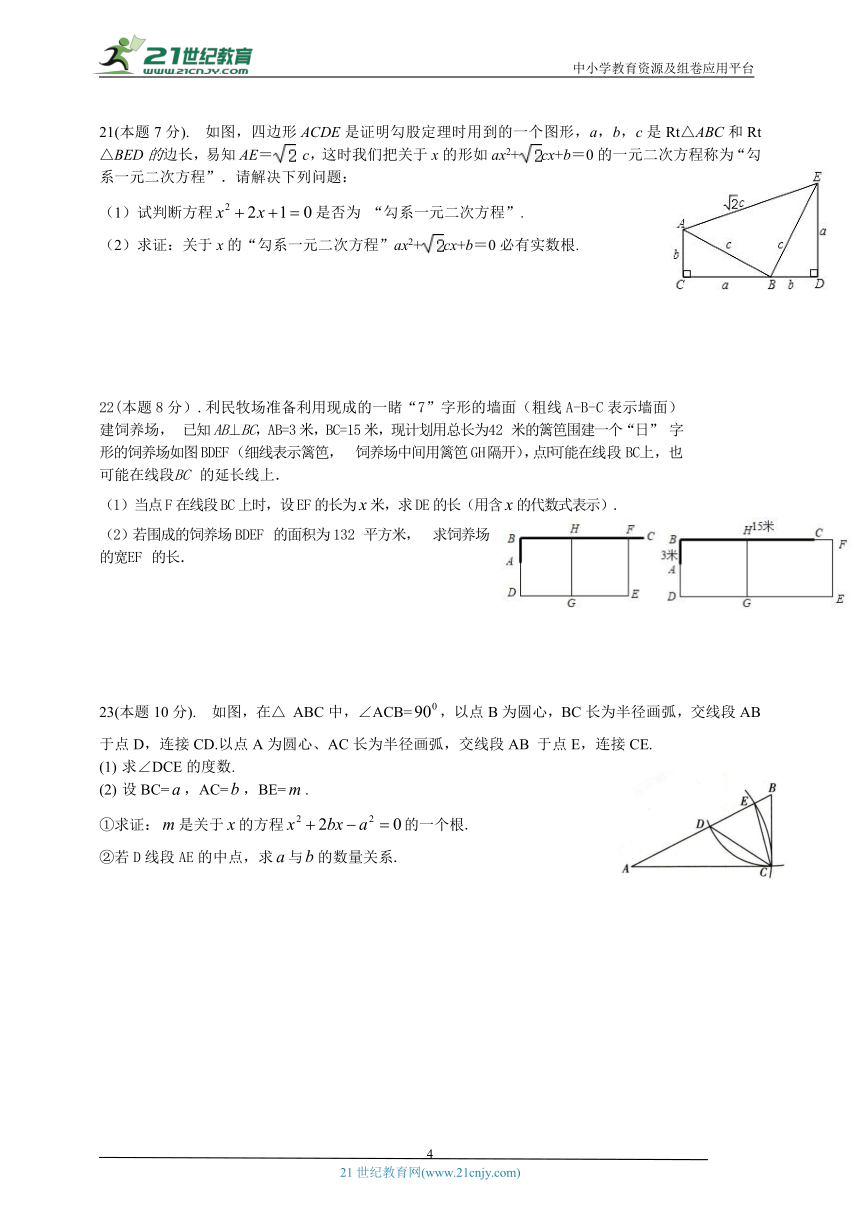
21(本题7分). 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED的边长,易知AE= c,这时我们把关于x的形如ax2+cx+b=0的一元二次方程称为“勾系一元二次方程”.请解决下列问题:
(1)试判断方程是否为 “勾系一元二次方程”.
(2)求证:关于x的“勾系一元二次方程”ax2+cx+b=0必有实数根.
22(本题8分).利民牧场准备利用现成的一睹“7”字形的墙面(粗线A-B-C表示墙面)建饲养场, 已知AB⊥BC,AB=3米,BC=15米,现计划用总长为 42 米的篱笆围建一个“日” 字形的饲养场 如图BDEF (细线表示篱笆, 饲养场中间用篱笆GH 隔开),点 F 可能在线段BC 上,也可能在线段 BC 的延长线上.
(1)当点F在线段BC上时,设EF的长为米,求DE的长(用含的代数式表示).
(2)若围成的饲养场 BDEF 的面积为 132 平方米, 求饲养场的宽 EF 的长.
23(本题10分). 如图,在△ ABC中,∠ACB=,以点B为圆心,BC长为半径画弧,交线段AB于点D,连接CD.以点A为圆心、AC长为半径画弧,交线段AB 于点E,连接CE.
求∠DCE的度数.
设BC=,AC=,BE=.
①求证:是关于的方程的一个根.
②若D线段AE的中点,求与的数量关系.
参考答案
选择题:
D
C 提示:原方程可化为,.
或.解得或.故选C.
C 提示:,∴方程没有实数根.故选C.
A
B
B 提示:.
.故选B.
C 提示:解方程,得,.∴此直角三角形的两边长分别为6和8.
①若6和8都是直角边,则第三边为斜边.则第三边的长为:;
②若8是斜边,则第三边为直角边.则第三边的长为:.
∴第三边的长为10或.故选C.
D 提示:由韦达定理得
故选D.
A 提示:剩余绿地经过平移,相当于一块长为,宽为的长方形.由题意得
,化为.解得或.,.故选A.
D 提示:∵原方程有实数根,.
化为,又,∴.
.解得..故选A.
填空题:
4 提示:由题意得.解得.
6 提示:由,得.,
..
提示:方程可化为.由韦达定理得,.
提示:把代入方程,得.是方程的一个根.由得.把代入方程得.也是方程的一个根..
3或6 提示:由题意得..解得或6.
或或 提示:∵点C在一次函数的图象上,∴可设点C的坐标为.由A(0,2)得OA=2.
当AC=OA=2时,则..化为.解得(舍去)或.
得.
当OC=OA=2时,则..解得.
得、.
解答题:
解:(1)方程化为,..
,.
(2)方程化为,..解得.
解:把代入方程,得.
.解得或.经检验,或.都满足题意.的值为-9或2.
解:(1),无论取什么实数,
,∴方程总有实数根.
(2)①若为腰,则中必有一个为1,不妨设,把代入方程,得.解得.此时方程化为.解得,..
则,不符合三角形的三边关系.故不能为腰.
②若不是腰,则都是腰,此时方程.有两个相等的实数根.
...此时方程化为.解得.
.∴△ABC的周长为:1+2+2=5.
解:(1)原方程可化为.由题意得,化为.解得.又,.的取值范围为且.
当时,方程化为.则,.
.
(1)解:方程是“勾系一元二次方程”.理由如下:方程可化为,由方程是“勾系一元二次方程”可知:
.,能构成直角三角形.∴方程是“勾系一元二次方程”.
(2)证明:∵关于x的方程ax2+cx+b=0有“勾系一元二次方程”,能构成直角三角形,且为斜边...
∴关于x的“勾系一元二次方程”ax2+cx+b=0必有实数根.
解:(1)由图可得,.
.∴DE的长为()米.
(2)①当点F在线段BC上时,由(1)知DE=45..解得或.当时,DE=45-3×4=33>15,不含题意,舍去..(米).
②当点F在BC延长线上时,CF=BF-BC=DE-BC=DE-15.∴DE+CF=42-AD-HG-EF=42-(.
∴DE+DE-15=45-.∴DE=30-..解得.当
时,CF=DE-15=(30-)-15=30-=-3<0,不合题意,舍去.
.(米). 答:饲养场的宽EF为11米或(10-2)米.
(1)解:由题意知BC=BD,AC=AE,∴∠BCD=∠4,∠ACE=∠3,∴∠DCE=∠ACE+∠BCD-∠ACB=∠3+∠4-=(∠1+∠B)+(∠2+∠A)-=(∠1+∠2)+(∠A+∠B)-=(-∠DCE)+-=-∠DCE.∴2∠DCE=.解得∠DCE=.
①证明:,.
,而方程的根
.
.是关于的方程的一个根.
②若D是AE的中点,则DE=AD==AC=.∴BE=BD-DE=BC-DE=.由①知BE=
...化为.,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版2024学年八年级下册数学第二章《一元二次方程》提高卷(附答案)
选择题(本题共10小题,每小题3分,共30分)
已知关于的方程是一元二次方程,则的取值范围是( )
B. C. D.
方程的解是( )
B. C. 或 D. 或
一元二次方程的根的情况是( )
有两个不相等的实数根 B. 有两个相等的实数根
C . 没有实数根 D. 无法确定
用配方法解方程,方程应变形为( )
B. C. D.
某银行经过两次降息,使一年存款的年利率由原来的2.25%降低至1.21%,设平均每次降息的百分率为,则满足方程( )
B.
C . D.
已知,(为任意实数),则的大小关系为( )
B. M
6或8 B. 8或10 C. 10或 D.
设是方程的两个根,则的值为( )
7 B. 8 C. 9 D. 10
如图所示,某市世纪广场有一块长为18、宽为15的长方形绿地,在绿地中开辟三条道路后,剩余绿地的面积为182,则的值为( )
2 B. 22 C. 2或22 D. 4或22
若方程x2+2(1+a)x+3a2+4ab+4b2+2=0有实数根,则=( )
B. - C. D.
填空题(本题共6小题,每小题3分,共18分)
若关于的一元二次方程有两个相等的实数根,则= .
若为实数,且,则= .
设是一元二次方程的两个根,则的值为 .
若关于的一元二次方程中,,,满足和则=
.
如图,在△ABC中,∠B=,AB=9cm,BC=12cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果点P、Q分别从点A、B同时出发,经过秒,使得△PBQ的面积为18.则= .
如图,直线OB是一次函数的图象,点A的坐标为(0,2),在直线OB上找点C,使得ΔACO是以OA为腰的等腰三角形,则点C的坐标为 .
解答题:(本大题有 7小题,共52分)
17(本题8分). 选用适当的方法解下列一元二次方程:
(2)
18(本题5分). 已知关于的一元二次方程有一个根是3,求的值.
19(本题7分). 已知关于的一元二次方程.
求证:无论取什么实数,方程总有实数根.
若等腰△ABC的一边长,另两边长恰好是这个方程的两个根,求△ABC的周长.
20(本题7分). 已知关于的一元二次方程有实数根.
求的取值范围.
当时,设原方程的两个实数根为,且,求的值.
21(本题7分). 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED的边长,易知AE= c,这时我们把关于x的形如ax2+cx+b=0的一元二次方程称为“勾系一元二次方程”.请解决下列问题:
(1)试判断方程是否为 “勾系一元二次方程”.
(2)求证:关于x的“勾系一元二次方程”ax2+cx+b=0必有实数根.
22(本题8分).利民牧场准备利用现成的一睹“7”字形的墙面(粗线A-B-C表示墙面)建饲养场, 已知AB⊥BC,AB=3米,BC=15米,现计划用总长为 42 米的篱笆围建一个“日” 字形的饲养场 如图BDEF (细线表示篱笆, 饲养场中间用篱笆GH 隔开),点 F 可能在线段BC 上,也可能在线段 BC 的延长线上.
(1)当点F在线段BC上时,设EF的长为米,求DE的长(用含的代数式表示).
(2)若围成的饲养场 BDEF 的面积为 132 平方米, 求饲养场的宽 EF 的长.
23(本题10分). 如图,在△ ABC中,∠ACB=,以点B为圆心,BC长为半径画弧,交线段AB于点D,连接CD.以点A为圆心、AC长为半径画弧,交线段AB 于点E,连接CE.
求∠DCE的度数.
设BC=,AC=,BE=.
①求证:是关于的方程的一个根.
②若D线段AE的中点,求与的数量关系.
参考答案
选择题:
D
C 提示:原方程可化为,.
或.解得或.故选C.
C 提示:,∴方程没有实数根.故选C.
A
B
B 提示:.
.故选B.
C 提示:解方程,得,.∴此直角三角形的两边长分别为6和8.
①若6和8都是直角边,则第三边为斜边.则第三边的长为:;
②若8是斜边,则第三边为直角边.则第三边的长为:.
∴第三边的长为10或.故选C.
D 提示:由韦达定理得
故选D.
A 提示:剩余绿地经过平移,相当于一块长为,宽为的长方形.由题意得
,化为.解得或.,.故选A.
D 提示:∵原方程有实数根,.
化为,又,∴.
.解得..故选A.
填空题:
4 提示:由题意得.解得.
6 提示:由,得.,
..
提示:方程可化为.由韦达定理得,.
提示:把代入方程,得.是方程的一个根.由得.把代入方程得.也是方程的一个根..
3或6 提示:由题意得..解得或6.
或或 提示:∵点C在一次函数的图象上,∴可设点C的坐标为.由A(0,2)得OA=2.
当AC=OA=2时,则..化为.解得(舍去)或.
得.
当OC=OA=2时,则..解得.
得、.
解答题:
解:(1)方程化为,..
,.
(2)方程化为,..解得.
解:把代入方程,得.
.解得或.经检验,或.都满足题意.的值为-9或2.
解:(1),无论取什么实数,
,∴方程总有实数根.
(2)①若为腰,则中必有一个为1,不妨设,把代入方程,得.解得.此时方程化为.解得,..
则,不符合三角形的三边关系.故不能为腰.
②若不是腰,则都是腰,此时方程.有两个相等的实数根.
...此时方程化为.解得.
.∴△ABC的周长为:1+2+2=5.
解:(1)原方程可化为.由题意得,化为.解得.又,.的取值范围为且.
当时,方程化为.则,.
.
(1)解:方程是“勾系一元二次方程”.理由如下:方程可化为,由方程是“勾系一元二次方程”可知:
.,能构成直角三角形.∴方程是“勾系一元二次方程”.
(2)证明:∵关于x的方程ax2+cx+b=0有“勾系一元二次方程”,能构成直角三角形,且为斜边...
∴关于x的“勾系一元二次方程”ax2+cx+b=0必有实数根.
解:(1)由图可得,.
.∴DE的长为()米.
(2)①当点F在线段BC上时,由(1)知DE=45..解得或.当时,DE=45-3×4=33>15,不含题意,舍去..(米).
②当点F在BC延长线上时,CF=BF-BC=DE-BC=DE-15.∴DE+CF=42-AD-HG-EF=42-(.
∴DE+DE-15=45-.∴DE=30-..解得.当
时,CF=DE-15=(30-)-15=30-=-3<0,不合题意,舍去.
.(米). 答:饲养场的宽EF为11米或(10-2)米.
(1)解:由题意知BC=BD,AC=AE,∴∠BCD=∠4,∠ACE=∠3,∴∠DCE=∠ACE+∠BCD-∠ACB=∠3+∠4-=(∠1+∠B)+(∠2+∠A)-=(∠1+∠2)+(∠A+∠B)-=(-∠DCE)+-=-∠DCE.∴2∠DCE=.解得∠DCE=.
①证明:,.
,而方程的根
.
.是关于的方程的一个根.
②若D是AE的中点,则DE=AD==AC=.∴BE=BD-DE=BC-DE=.由①知BE=
...化为.,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
