1.1 锐角三角函数(1)
图片预览



文档简介
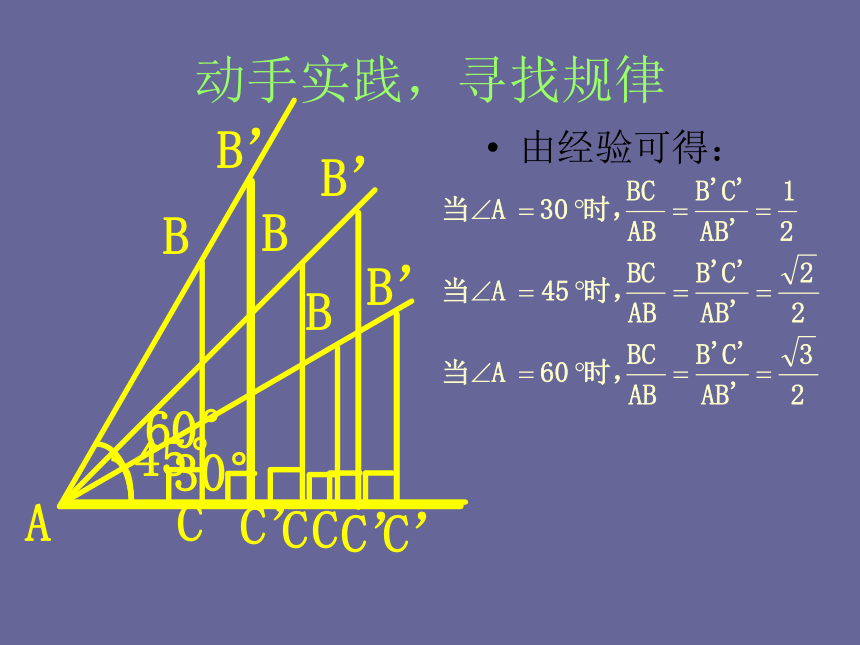
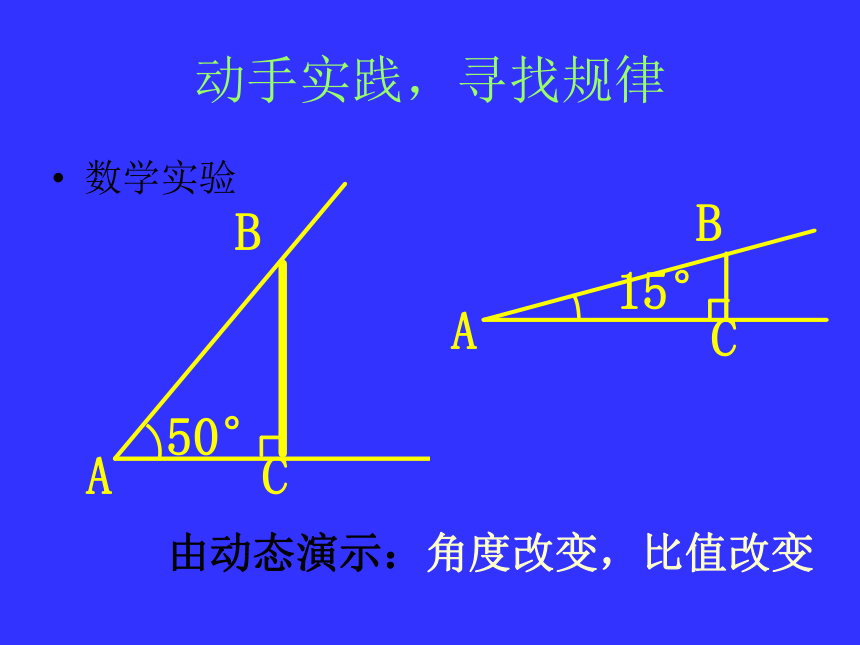
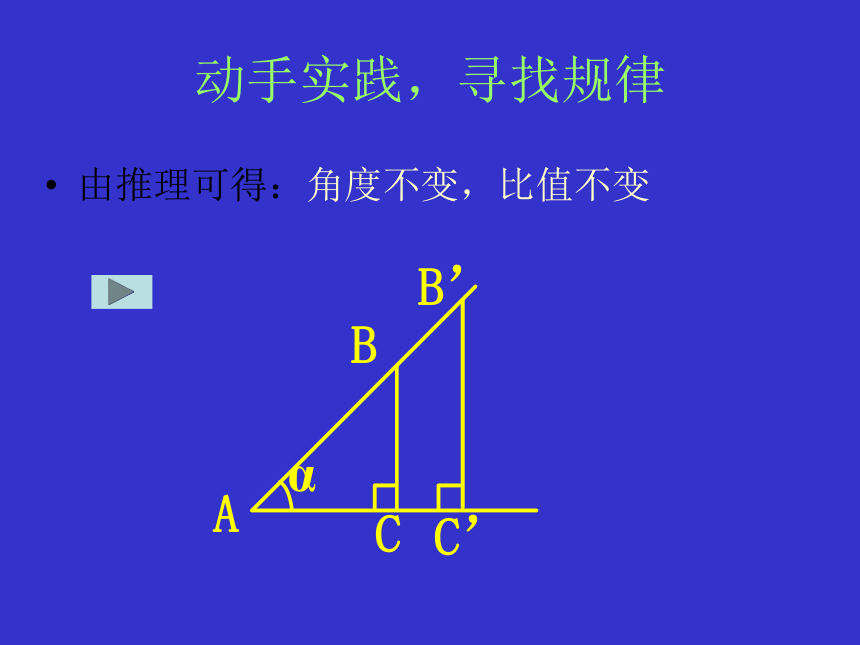
课件26张PPT。浙教版义务教育课程标准实验教科书数学九年级下册1.1锐角三角函数(1)从数学到实际,回归情景已知一辆汽车从高架桥引桥的入口到高架桥路面总共行驶了大约30m的距离,若已知该段引桥的坡角约为15°,请问高架桥的路面离地大约多少米? 你想知道怎样算出高架桥的路面离地吗?45°C60°动手实践,寻找规律 AB’C’30°BCBCB’C’BB’C’由经验可得:15°C动手实践,寻找规律 AB50°CBA数学实验由动态演示:角度改变,比值改变动手实践,寻找规律ABCαB’C’由推理可得:角度不变,比值不变
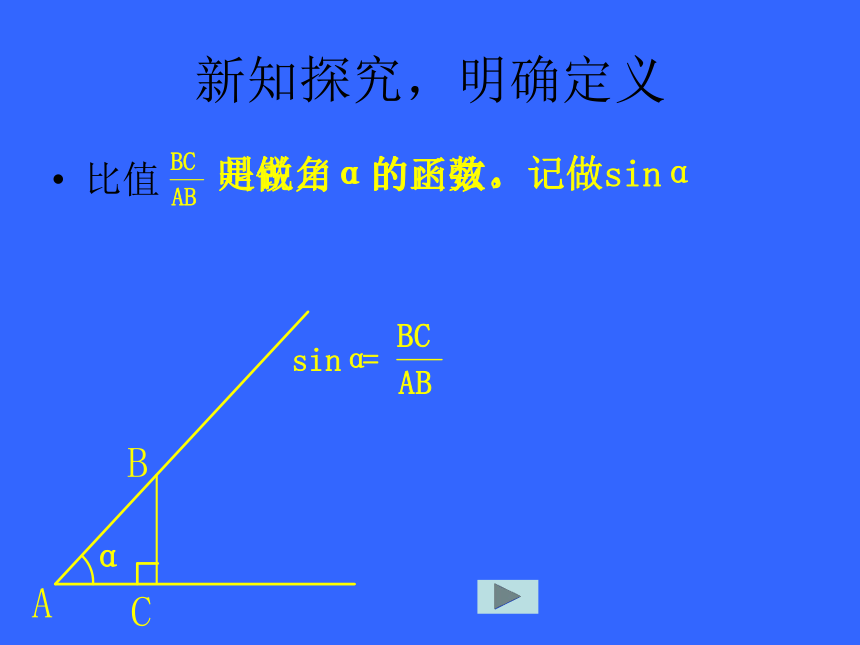
新知探究,明确定义 比值叫做∠α的正弦是锐角α的函数。,记做sinαA BC
比值
比值新知探究,明确定义比值A叫做∠α的正弦,记做sinα BC 叫做∠α的余弦,记做cosα叫做∠α的正切,记做tanα锐角α的正弦、余弦、正切
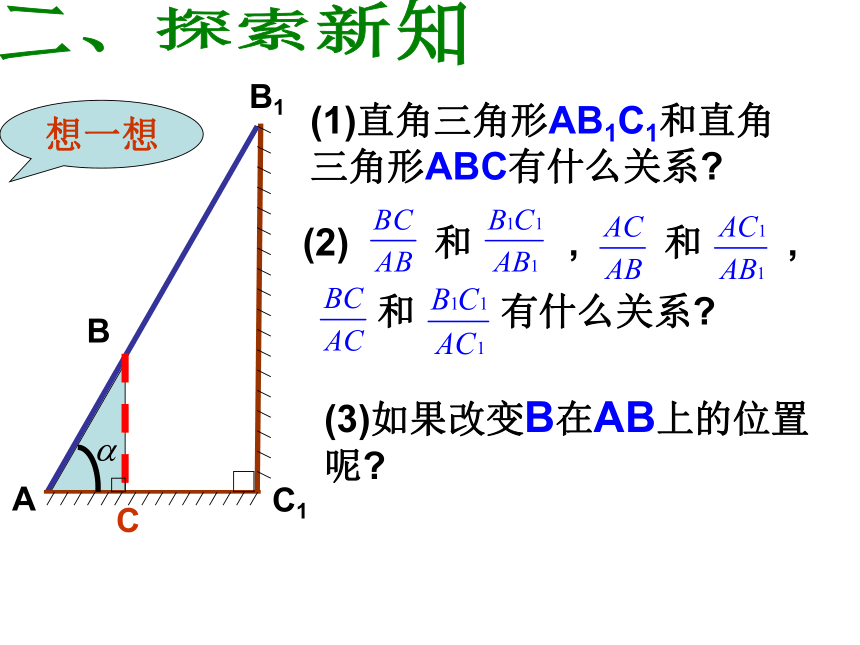
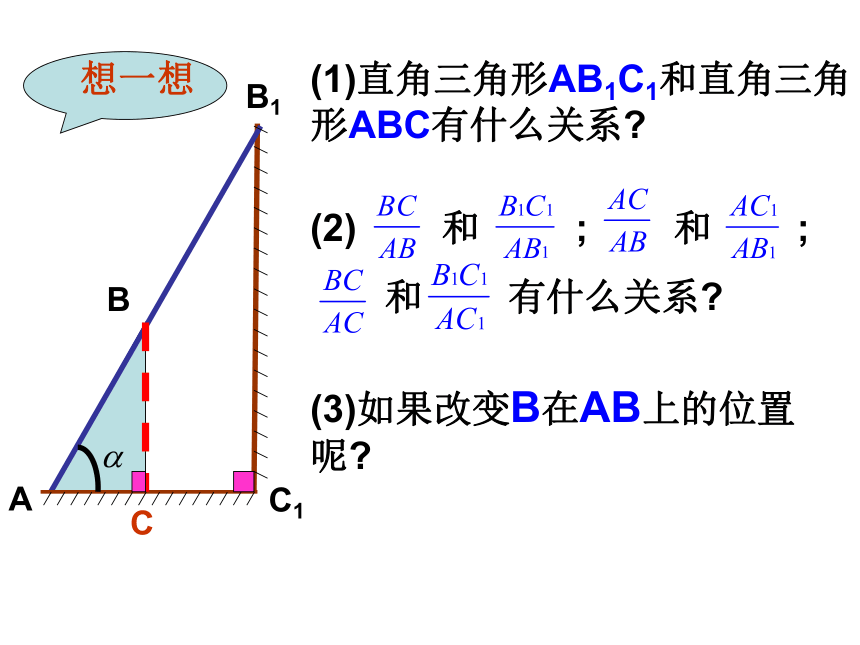
统称为∠α的三角函数 AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角形ABC有什么关系?(3)如果改变B在AB上的位置呢?二、探索新知 AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(3)如果改变B在AB上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(3)如果改变B在AB上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(3)如果改变B在AB上的位置呢? AB1 C1 CB想一想(3)如果改变B在AB上的位置呢?(1)直角三角形AB1C1和直角三角 形ABC有什么关系? A CB新知探究,明确定义如图,在Rt⊿ABC中,∠C=Rt∠ ∠A
的
对
边∠A的邻边斜边∠B
的
邻
边∠B的对边锐角函数三角练习拓展,层层递进
例1.在Rt⊿ABC中,∠C=Rt∠,AB=5,BC=3,求锐角∠A的各三角函数值(书P5)
1。在Rt⊿ABC中,∠C=Rt∠,AC=8,BC=6,求锐角∠A的各三角函数值
(书P6作业题2)变2。在Rt⊿ABC中,∠C=Rt∠,
求锐角∠A的余弦 变变3。已知锐角∠α的顶点在原点,始边在轴的正半轴上,终边上一点P的坐标(1,3),则tanα的值为 。 变变变13例2 如图:在Rt△ABC中,
∠B=900,AC=200,
sinA=0.6.求:BC的长. 如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB
提示:过点A作AD垂直于BC于D.拓展延伸探索在直角三角形中,∠A+∠B=90sinA和cosB, cosA和sinB有什么关系?sinA=cosB cosA=sinB (∠A+∠B=90。)回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的正切,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.在Rt⊿ABC中,∠C=Rt∠,
CD⊥AB,求锐角∠DCB的余弦 D变变归纳小结,反思提高我来说从数学到实际,回归情景已知一辆汽车从高架桥引桥的入口到高架桥路面总共行驶了大约30m的距离,若已知该段引桥的坡角约为15°,请问高架桥的路面离地大约多少米? 回归情景,解决问题
新知探究,明确定义 比值叫做∠α的正弦是锐角α的函数。,记做sinαA BC
比值
比值新知探究,明确定义比值A叫做∠α的正弦,记做sinα BC 叫做∠α的余弦,记做cosα叫做∠α的正切,记做tanα锐角α的正弦、余弦、正切
统称为∠α的三角函数 AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角形ABC有什么关系?(3)如果改变B在AB上的位置呢?二、探索新知 AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(3)如果改变B在AB上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(3)如果改变B在AB上的位置呢? AB1 C1 CB想一想(1)直角三角形AB1C1和直角三角 形ABC有什么关系?(3)如果改变B在AB上的位置呢? AB1 C1 CB想一想(3)如果改变B在AB上的位置呢?(1)直角三角形AB1C1和直角三角 形ABC有什么关系? A CB新知探究,明确定义如图,在Rt⊿ABC中,∠C=Rt∠ ∠A
的
对
边∠A的邻边斜边∠B
的
邻
边∠B的对边锐角函数三角练习拓展,层层递进
例1.在Rt⊿ABC中,∠C=Rt∠,AB=5,BC=3,求锐角∠A的各三角函数值(书P5)
1。在Rt⊿ABC中,∠C=Rt∠,AC=8,BC=6,求锐角∠A的各三角函数值
(书P6作业题2)变2。在Rt⊿ABC中,∠C=Rt∠,
求锐角∠A的余弦 变变3。已知锐角∠α的顶点在原点,始边在轴的正半轴上,终边上一点P的坐标(1,3),则tanα的值为 。 变变变13例2 如图:在Rt△ABC中,
∠B=900,AC=200,
sinA=0.6.求:BC的长. 如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB
提示:过点A作AD垂直于BC于D.拓展延伸探索在直角三角形中,∠A+∠B=90sinA和cosB, cosA和sinB有什么关系?sinA=cosB cosA=sinB (∠A+∠B=90。)回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的正切,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.在Rt⊿ABC中,∠C=Rt∠,
CD⊥AB,求锐角∠DCB的余弦 D变变归纳小结,反思提高我来说从数学到实际,回归情景已知一辆汽车从高架桥引桥的入口到高架桥路面总共行驶了大约30m的距离,若已知该段引桥的坡角约为15°,请问高架桥的路面离地大约多少米? 回归情景,解决问题
