5.4一元一次不等式组（1）

课件23张PPT。5.4一元一次不等式组(1)海宁二中 朱安娜学习目标和学习方法1.理解一元一次不等式组及其解集的意义,会解一元一次不等式组。
2.培养学生进行数学类比学习的能力。
3.感受"化难为易"、化未知为已知的数学思想
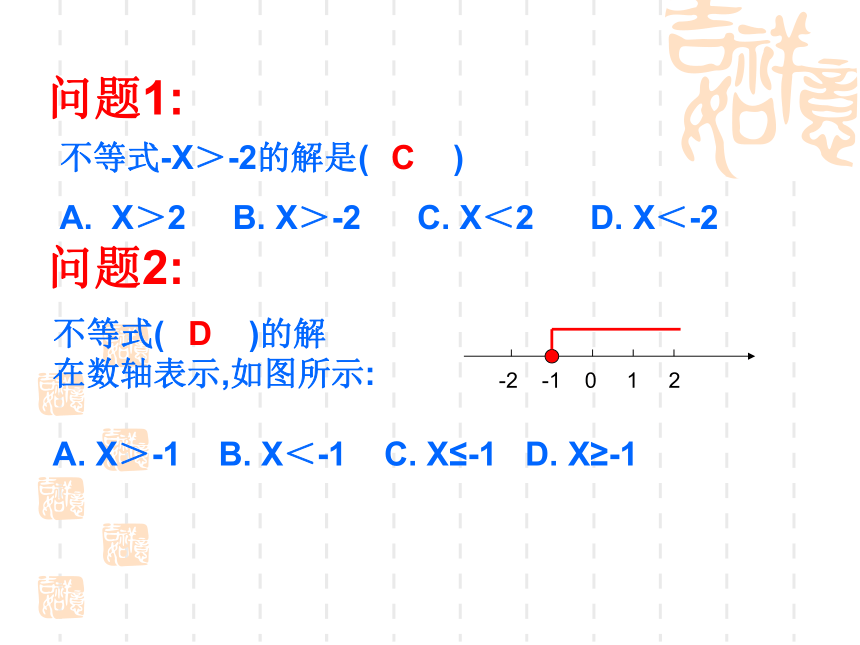
问题1:不等式-X＞-2的解是( )
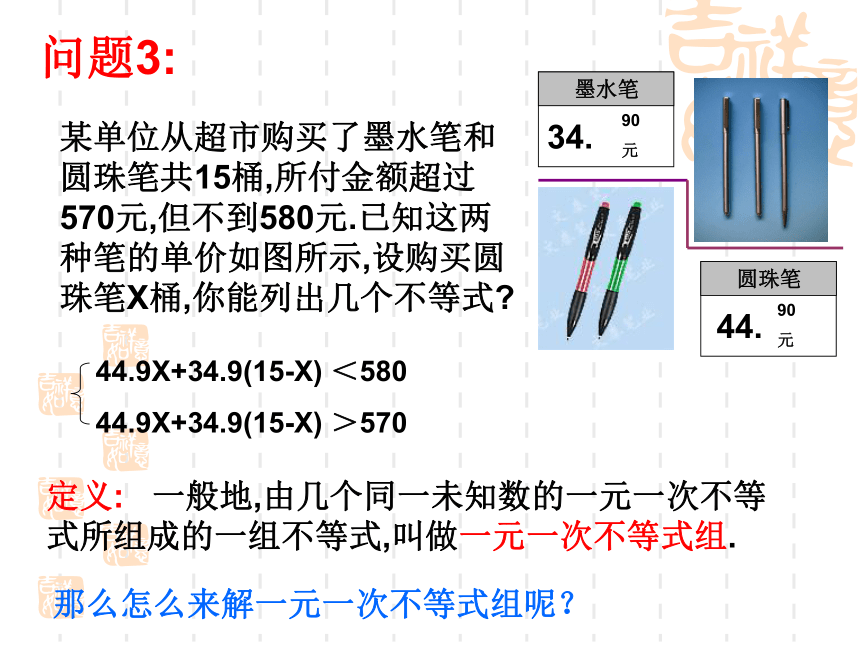
A. X＞2 B. X＞-2 C. X＜2 D. X＜-2 问题2:CD某单位从超市购买了墨水笔和圆珠笔共15桶,所付金额超过570元,但不到580元.已知这两种笔的单价如图所示,设购买圆珠笔X桶,你能列出几个不等式?问题3:44.9X+34.9(15-X) ＜580
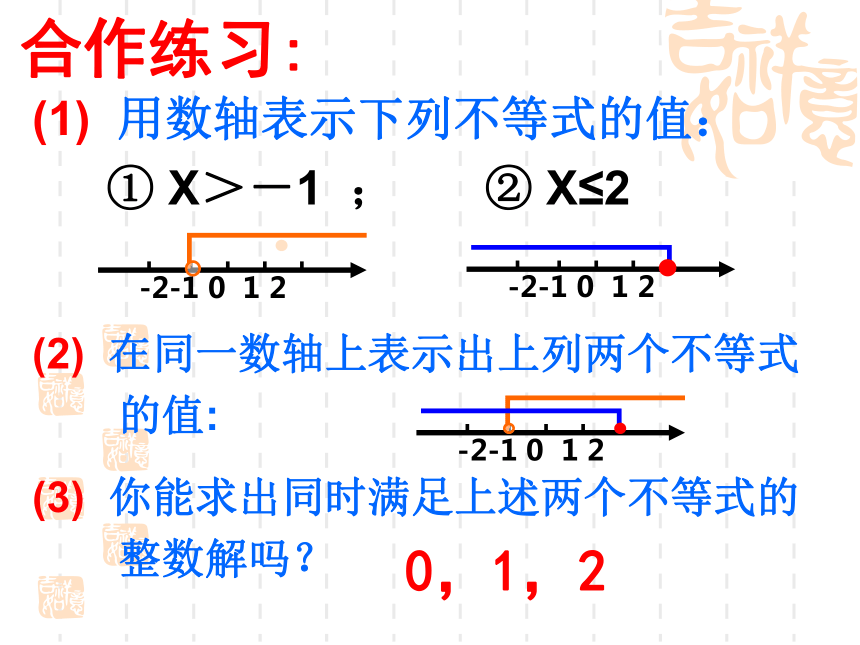
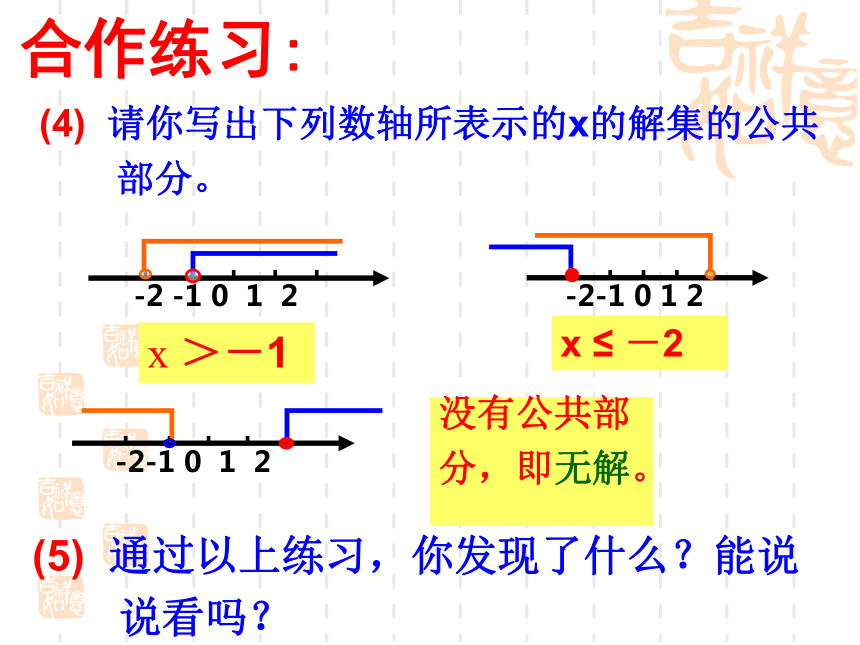
44.9X+34.9(15-X) ＞570定义: 一般地,由几个同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.那么怎么来解一元一次不等式组呢？合作练习:① X＞－1 ；　 ② X≤2 (1) 用数轴表示下列不等式的值：(2) 在同一数轴上表示出上列两个不等式
　　的值:(3) 你能求出同时满足上述两个不等式的
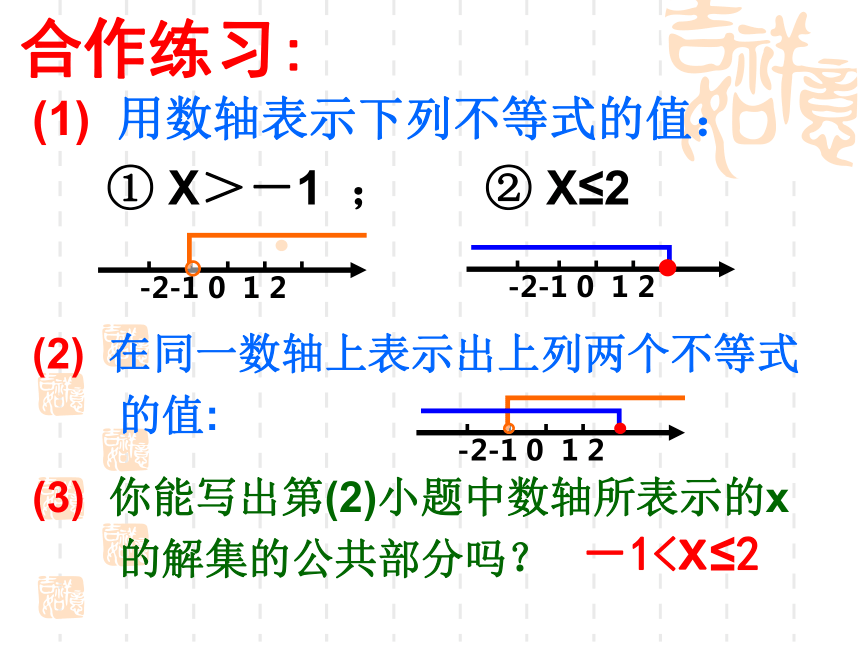
　　整数解吗？0，1，2合作练习:① X＞－1 ；　 ② X≤2 (1) 用数轴表示下列不等式的值：(2) 在同一数轴上表示出上列两个不等式
　　的值:(3) 你能写出第(2)小题中数轴所表示的x
　　的解集的公共部分吗？－1　　部分。x ＞－1x ≤ －2没有公共部
分，即无解。(5) 通过以上练习，你发现了什么？能说
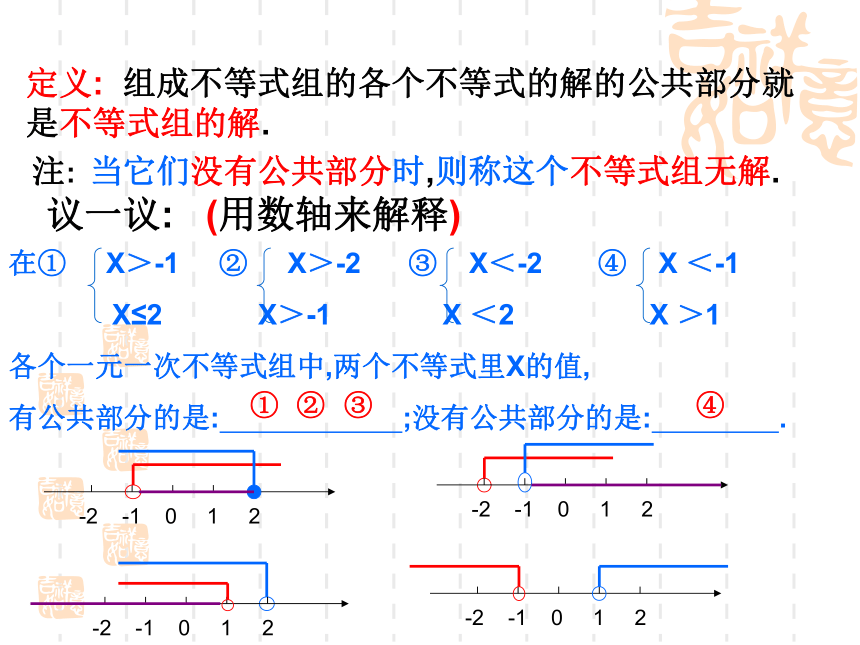
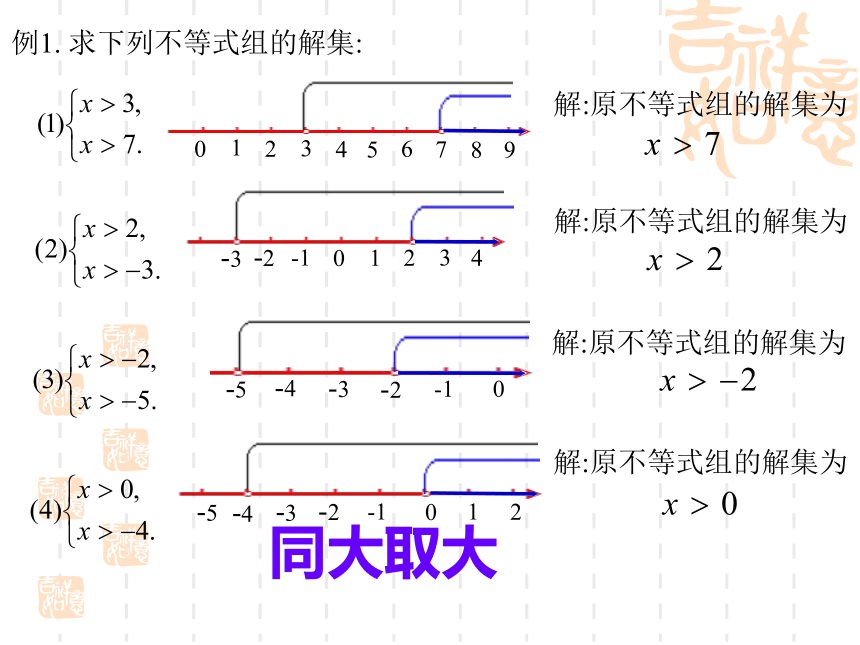
　　说看吗？议一议: (用数轴来解释)②④定义: 组成不等式组的各个不等式的解的公共部分就是不等式组的解. ① ③ 注: 当它们没有公共部分时,则称这个不等式组无解.例1. 求下列不等式组的解集:解:原不等式组的解集为解:原不等式组的解集为解:原不等式组的解集为解:原不等式组的解集为同大取大例1. 求下列不等式组的解集:解:原不等式组的解集为解:原不等式组的解集为解:原不等式组的解集为解:原不等式组的解集为同小取小例1. 求下列不等式组的解集:解:原不等式组的解集为解:原不等式组的解集为解:原不等式组的解集为解:原不等式组的解集为大小小大中间找例1. 求下列不等式组的解集:解:原不等式组无解.解:原不等式组无解.解:原不等式组无解.解:原不等式组无解.大大小小是无解同大取大X＞a同小取小X＜b大小小大取中间b ≤ X＜a大小等同取等值X＝a大大小小则无解无解文字记忆数学语言图形解集及记忆方法比一比：看谁反应快运用规律求下列不等式组的解集：1. 同大取大，
2.同小取小；
3.大小小大中间找，
4.大大小小是无解。解一元一次不等式组的步骤:
(1) 分别求出各不等式的解
(2) 将它们的解表示在同一数轴上
(3) 求原不等式组的解(即取它们解的公共部分).想一想(1)如果让你解一个不等式组,你认为应该按怎样的步骤来操作?(2)解不等式组与解方程组有何区别?解不等式组只须先解出每个不等式的解，然后再取公共部分。
解方程组则往往先要消元，然后求出每个未知数的值，最后写出方程组的解。解:解不等式①,得X＞-1解不等式②,得X≤6把①, ②两不等式的解表示在数轴上(如图)所以原不等式组的解是 -1＜X≤6分析: 根据一元一次不等式组解的意义, 只要求出各不等式的解的公共部分即可.此题与上题有何不同?解: 解不等式①,得 X＜
解不等式②,得 X＞
把① ,②两个不等式的解表示在数轴上所以原不等式组无解练一练:1.解下列各一元一次不等式组 （课内练习2）某单位从超市购买了墨水笔和圆珠笔共15桶,所付金额超过570元,但不到580元.已知这两种笔的单价如图所示,设购买圆珠笔X桶,回答问题3:44.9X+34.9(15-X) ＜580
44.9X+34.9(15-X) ＞570解得4.65＜X＜5.65.
∵X为正整数
∴X=5
15-X=15-5=10
答:原珠笔买5盒,墨水笔买10盒你能求出X的值吗？1.解不等式组: 2-x＜x≤6-2xA解为 1＜x≤2思考题:2-x＜xx≤6-2x(1)一元一次不等式组的概念
(2)一元一次不等式组的解的概念
(3)解一元一次不等式组的步骤和解的四种情况.
(4)如果不等式中有等号，则等号要跟着原来的不等号。小结: (1)作业本5.4(1)
(2)同步练习布置作业再见