4.3代数式的值

课件17张PPT。欢迎各位教师莅临指导！４.３ 代数式的值引入篇：2009年10月1日，北京时间10:00整，国庆60周年阅兵式在北京天安门隆重举行。一流的组织领导，一流的武器装备，一流的精神风貌，全面展现了我国强大的国防。此时，与我们隔海相望的在日本的华人，他们是当地时间几点看的阅兵式呢？引入篇：发散思维，大胆猜想！（1）东京时间和北京时间
见表，可以看出北京与东
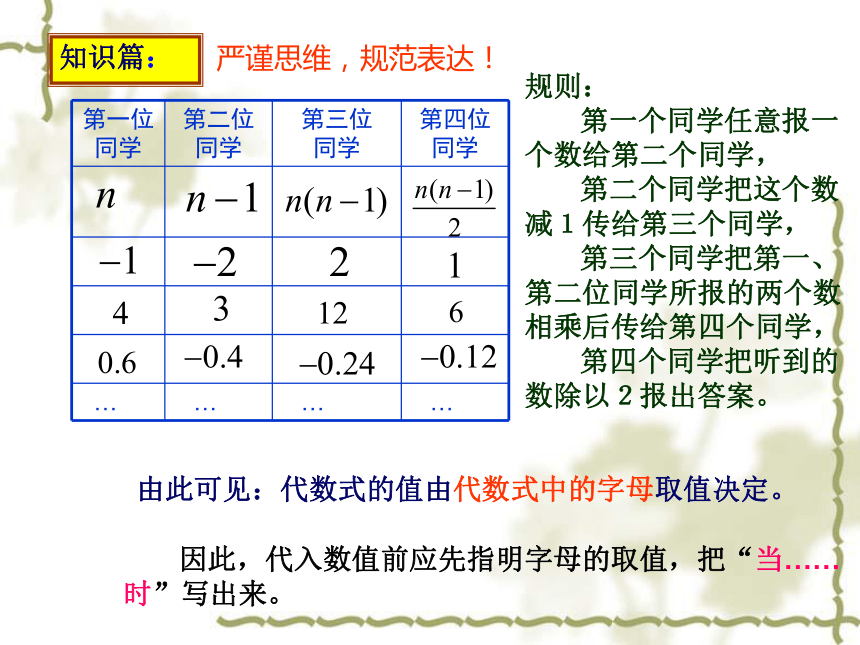
京的时差相差 时。（3）第29届奥运会开幕式于 2008年8月8日晚上8时在中国国家体育馆（鸟巢）举行。 问开幕式的东京时间是几时？知识篇：发散思维，大胆表达！ 一般地，用数值代替代数式里的字母，计算后所得的结果，叫做代数式的值。 求代数式的值的步骤: (1)代入，(2)计算。知识篇：严谨思维，规范表达！传数游戏规则：每四位同学为一组，做一个传数游戏。
第一个同学任意报一个数给第二个同学，
第二个同学把这个数减１传给第三个同学，
第三个同学把第一、第二位同学所报的两个
数相乘后传给第四个同学，
第四个同学把听到的数除以２报出答案。
知识篇： 由此可见：代数式的值由代数式中的字母取值决定。 因此，代入数值前应先指明字母的取值，把“当……时”写出来。知识篇：严谨思维，规范表达！规则：
第一个同学任意报一个数给第二个同学，
第二个同学把这个数减１传给第三个同学，
第三个同学把第一、第二位同学所报的两个数相乘后传给第四个同学，
第四个同学把听到的数除以２报出答案。1、求代数式的值的步骤: (1)代入，(2)计算；
2、具体书写过程：当、抄、代、算。
注意事项：
（1）代入数值时必须把原来省略的乘号添上；
（2）负数、分数代入时要根据情况适时加上括号；
（3）计算时，应注意运算顺序。小结：知识篇：严谨思维，规范表达！学
以
致
用知识篇：严谨思维，规范表达！ 4、如图， 这是用100米的篱笆围成一个有一边靠墙的长方形的饲养场，设饲养场与墙垂直的一边为x米。（1）用代数式表示饲养场的面积。（2）当x分别为20米，25米，30米时，围成的面积分别为多少平方米？
学
以
致
用知识篇：严谨思维，规范表达！按右边图示的程序计算，若开始输入的n值为3，则最后输出的结果是 。 231输入n计算 的值＞200输出结果你能读懂吗?学
以
致
用知识篇：严谨思维，规范表达！挑战自我相同的代数式可以看作一个字母——整体代换。提高篇：灵活运用，挑战自我！有趣的“3x+1”问题现有两个代数式：
如果随意给出一个正整数，记为x，那么利用这个正整数，都可以根据代数式（1）或（2）求出一个对应值。
我们约定一个规则：若正整数x为奇数，我们就根据（1）式求对应值；若正整数x为偶数，我们就根据 （2）式求对应值。例如，根据这种规则，若取正整数x为18（偶数），则由（2）式求得对应值为9；而正整数9（奇数），由（1）式求得对应值为28；同样，正整数28（偶数）对应14……。我们感兴趣的是，从某一个正整数出发，不断地这样对应下去，会是一个什么样的结果呢？也许这是一个非常吸引人的数学游戏。探究篇：锲而不舍，感受奇妙！ 下面我们以正整数18为例,不断地做下去,如下图所示，最后竟出现了一个循环：4，2，1，4，2，1，…….91828147221120401326521734105168421 再取一个奇数试试看。比如取x为21，如下图所示，结果是一样的——仍是一个同样的循环.168421213264探究篇：锲而不舍，感受奇妙！ 大家可以随意再取一些正整数试一试，结果一定同样奇妙——最后总是落入4、2、1的“黑洞”。有人把这个游戏称为“3x+1”问题。
是不是从所有的正整数出发，都落入4、2、1的“黑洞”而无一例外呢？有人动用计算机，试遍了从1到
的所有正整数，结果都是成立的。
遗憾的是，这个结论至今还没有人给出数学证明（因为“验证”得再多，也是有限多个，不可能把正整数全部“验证”完毕）。这种现象是否可以推广到整数范围？大家不妨取几个负整数或0试一试。探究篇：锲而不舍，感受奇妙！ 通过这节课的学习,
你有什么收获同大家一起分享吗?1、求代数式的值的步骤:(1)代入,(2)计算；
2、具体书写过程：当、抄、代、算。
3、求代数式的值的注意事项：
（1）代入数值时，应把原来省略的乘号添上；
（2）负数、分数代入时，应根据情况适时加上括号；
（3）计算时，应注意运算顺序。
4、求代数式的值可以解决许多实际问题；
5、相同的代数式可以看作一个字母——整体代换。
回顾篇：畅所欲言，分享收获！