2.3 一元二次方程的应用 同步分层作业(含解析)
文档属性
| 名称 | 2.3 一元二次方程的应用 同步分层作业(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 908.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-27 17:31:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2.3 一元二次方程的应用 同步分层作业
1.春季是流感的高发时期,某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,则可列方程( )
A.1+x+x2=49 B.x+x2=49 C.(1+x)2=49 D.x+x(1+x)=49
2.某地积极宣传和推广“吃农家饭,品农家菜,干农家活”乡村体验式旅游项目,去年该地旅游产业获利50万元,若计划明年旅游产业获利72万元,那么该地这两年旅游产业获利的年平均增长率应为( )
A.44% B.14.4% C.20% D.10%
3.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,求每个支干长出多少小分支.设每个支干长出x小分支,那么根据题意可以列方程为( )
A.1+x+x2=91 B.1+x+x(1+x)=91 C.1+x+(1+x)2=91 D.1+(1+x)+(1+x)2=91
4.现将一张照片【长14英寸,宽10英寸】贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同均为a英寸,如图所示.已知矩形衬纸的面积为照片面积的2倍,则下列所列方程正确的是( )
A.2(10+a)(14+a)=14×10 B.2(10+2a)(14+2a)=14×10
C.(10+a)(14+a)=2×14×10 D.(10+2a)(14+2a)=2×14×10
5.某校自启动“书香校园 悦读成长”工程以来,成效显著,形成人人爱读书的良好氛围.该校图书馆三月份借出图书490本,五月份借出图书810本,设这两个月借出的图书平均每月增长率为x,则下列列出的方程正确的是( )
A.810(1﹣x)2=490 B.490(1+x)2=810 C.810(1﹣2x)=490 D.490(1+2x)=810
6.某地足球联赛中,参赛的每两个队之间都需要进行一场比赛,共比赛了45场.设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x+1)=45 B. C.x(x﹣1)=45 D.
7.某商店原来每天可销售某种水果100kg,每千克盈利7元,为了减少库存,经市场调查,如果这种水果每千克降价1元,那么每天可多售出30kg,若要每天盈利800元,则每千克应降价多少元?设每千克应降价x元,则所列方程是( )
A.(100+x)(7+x)=800 B.(100+30x)(7﹣x)=800
C.(100+30x)(7+x)=800 D.(100+x)(7﹣30x)=800
8.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.设动点P运动时间为t(t>0),当PQ=BC时,则t的值为 .
9.一个两位数,个位数字与十位数字之和是5,十位数字与个位数字对调后所得的数与原数相乘,得736,这个两位数是 .
10.国庆期间,某博物馆展出的珍贵文物吸引了众多游客.通过这些文物,人们仿佛穿越时空,与历史对话,这不仅丰富了精神生活,也促进了文化的传承与发展.据统计,博物馆10月1日接待的人数比9月30日的2倍多0.2万人,这两天共接待2.9万人.
(1)求博物馆10月1日接待游客的人数;
(2)10月2日、3日游客继续增加,据统计10月3日接待游客2.88万人,预计10月4日游客数量将达到高峰.为使游客有较好的体验效果,规定人数达到3.5万人时,将会采取临时限流措施.按10月2日、3日的日平均增长率计算,10月4日是否需要临时限流?
11.随着科技的不断进步,人工智能(AI)正逐渐渗透到我们的生活和工作.从家庭助手到自动驾驶汽车,再到智能医疗,AI的应用前景广阔且充满无限可能.某人工智能科技体验馆在十一假期间为学生们制订了丰富多彩的体验活动,团体票收费标准为:如果人数不超过10人,人均费用为240元;如果人数超过10人,每增加1人,人均费用降低5元,但人均旅游费用不得低于170元.
(1)若有14人参加旅游,人均费用是 元.
(2)某兴趣小组的学生们去参加体验活动,团体票的费用共3600元,求参加活动的学生人数.
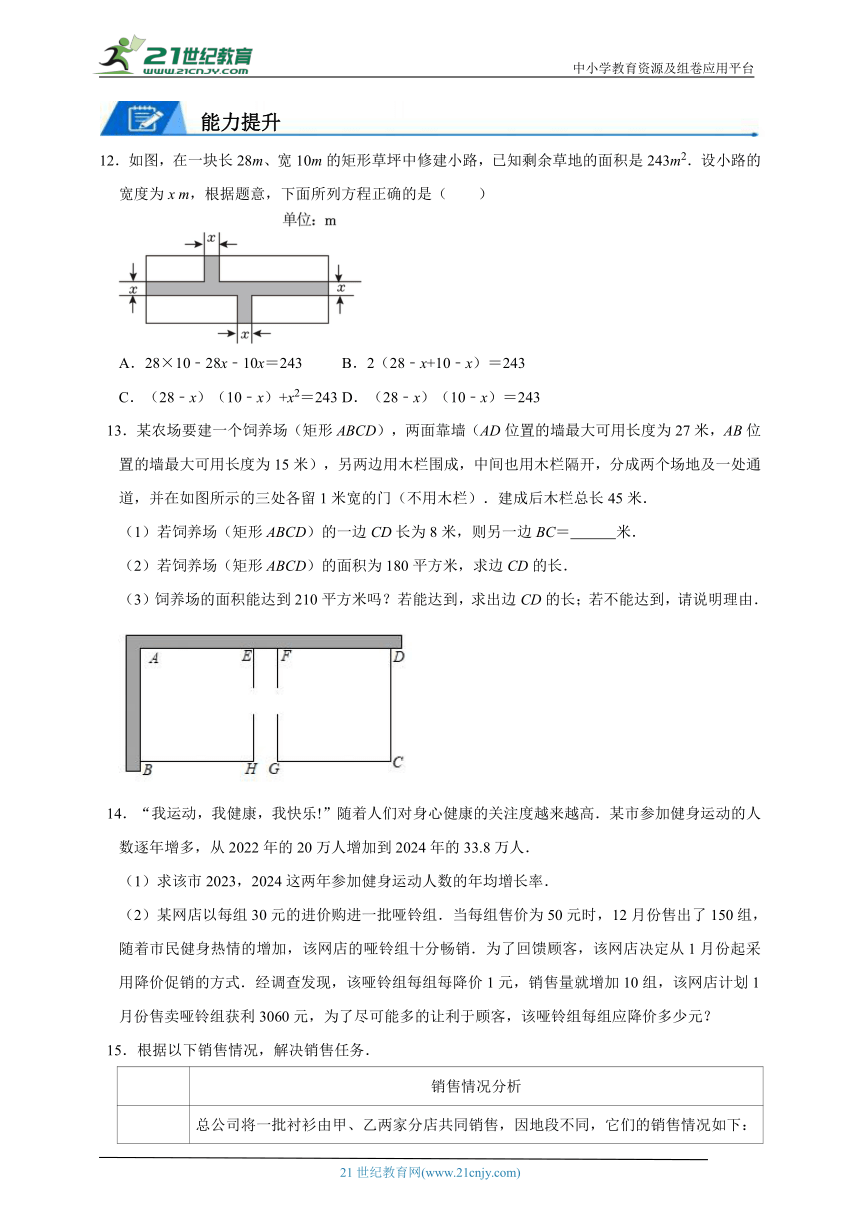
12.如图,在一块长28m、宽10m的矩形草坪中修建小路,已知剩余草地的面积是243m2.设小路的宽度为x m,根据题意,下面所列方程正确的是( )
A.28×10﹣28x﹣10x=243 B.2(28﹣x+10﹣x)=243
C.(28﹣x)(10﹣x)+x2=243 D.(28﹣x)(10﹣x)=243
13.某农场要建一个饲养场(矩形ABCD),两面靠墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.
(1)若饲养场(矩形ABCD)的一边CD长为8米,则另一边BC= 米.
(2)若饲养场(矩形ABCD)的面积为180平方米,求边CD的长.
(3)饲养场的面积能达到210平方米吗?若能达到,求出边CD的长;若不能达到,请说明理由.
14.“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2022年的20万人增加到2024年的33.8万人.
(1)求该市2023,2024这两年参加健身运动人数的年均增长率.
(2)某网店以每组30元的进价购进一批哑铃组.当每组售价为50元时,12月份售出了150组,随着市民健身热情的增加,该网店的哑铃组十分畅销.为了回馈顾客,该网店决定从1月份起采用降价促销的方式.经调查发现,该哑铃组每组每降价1元,销售量就增加10组,该网店计划1月份售卖哑铃组获利3060元,为了尽可能多的让利于顾客,该哑铃组每组应降价多少元?
15.根据以下销售情况,解决销售任务.
销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,它们的销售情况如下:
店面 甲店 乙店
日销售情况 每天可售出20件,每件盈利40元. 每天可售出32件,每件盈利30元.
市场调查 经调查发现,每件衬衫每降价1元,甲、乙两家店一天都可多售出2件.
情况设置 设甲店每件衬衫降价a元,乙店每件衬衫降价b元.
任务解决
任务1 甲店每天的销售量 (用含a的代数式表示).乙店每天的销售量 (用含b的代数式表示).
任务2 当a=5,b=4时,分别求出甲、乙店每天的盈利.
任务3 总公司规定两家分店下降的价格必须相同,请求出每件衬衫下降多少元时,两家分店一天的盈利和为2244元.
16.在矩形ABCD中,AB=10cm,BC=12cm,点P从点A开始沿边AB向终点B以2cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以4cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒(t>0).
(1)当t为何值时,PQ的长度等于10cm?
(2)是否存在t的值,使得五边形APQCD的面积等于104cm2?若存在,请求出此时t的值;若不存在,请说明理由.
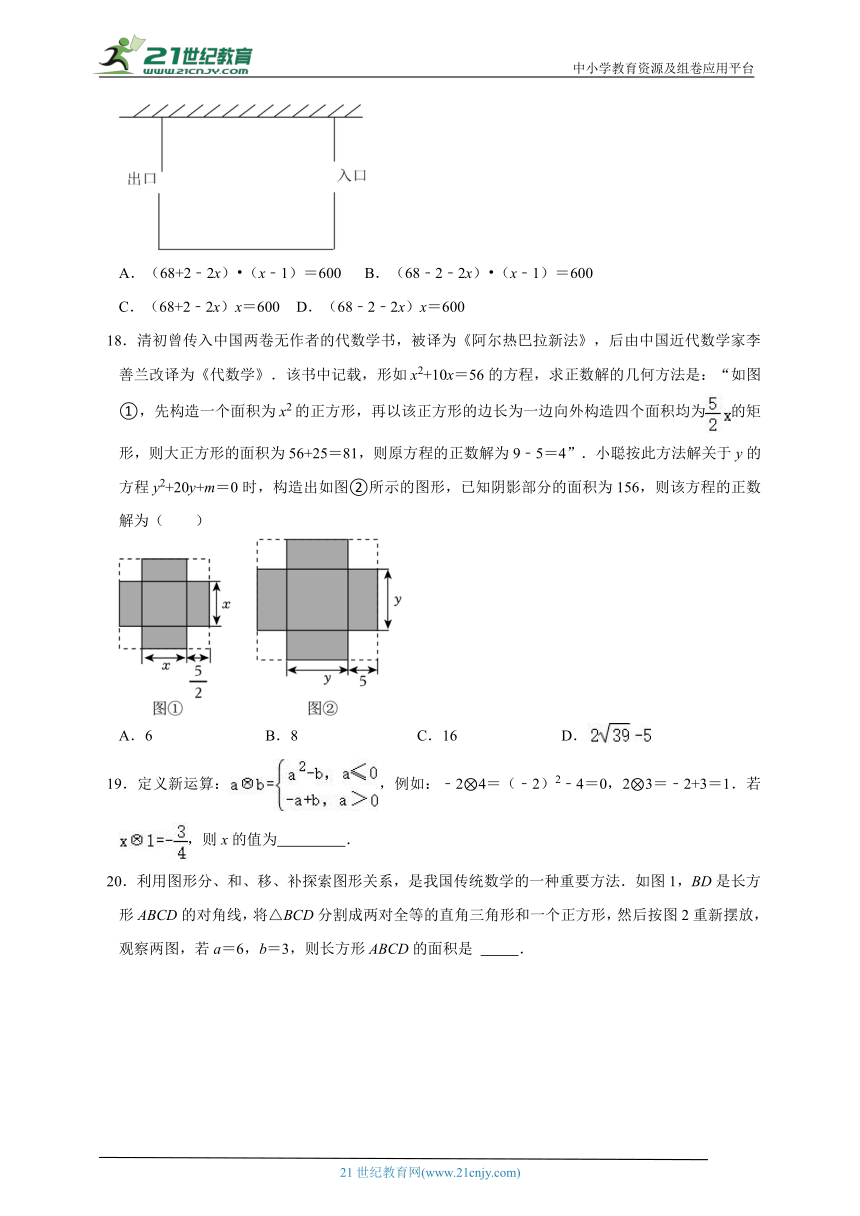
17.布置某艺术中心的会场时,工作人员准备利用35米长的地为一边,用68米隔栏绳围另三边,设立一个面积为600平方米的长方形等候区,如图,为了方便群众进出,在两边各空出一个1米的出入口(出入口不用隔栏绳).如果设这个长方形垂直于墙的一边长为x米,那么可以列出关于x的方程( )
A.(68+2﹣2x) (x﹣1)=600 B.(68﹣2﹣2x) (x﹣1)=600
C.(68+2﹣2x)x=600 D.(68﹣2﹣2x)x=600
18.清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
19.定义新运算:,例如:﹣2 4=(﹣2)2﹣4=0,2 3=﹣2+3=1.若,则x的值为 .
20.利用图形分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是长方形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=6,b=3,则长方形ABCD的面积是 .
21.根据以下素材,探索完成任务.
背景素材
素材1 随着数字技术、新能源、新材料等不断突破,我国创造业发展迎来重大机遇,天府科技园工作实验室借助智能化,对某款电动车的零部件进行一体化加工,以相同的生产效率提升,该零件7月份生产500个,9月份生产720个.
素材2 该园工作实验室的零部件成本为30元/个,销售一段时间后发现,当零部件售价为50元/个时,月销售量为800个,若在此基础上售价每下降2元,则月销售量将增加20个.为刺激经济的快速增长,政府给予实验室支持,当销量不低于900个时,每个将有5元的科技创新补贴.
问题解决
任务1 工作实验室从7月份到9月份生产数量的平均增长率;
任务2 使工作实验室月销售利润达到13500元,而且尽可能让车企得到实惠,社会普及增加,则该零件的实际售价应定为多少元?
答案与解析
1.春季是流感的高发时期,某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,则可列方程( )
A.1+x+x2=49 B.x+x2=49 C.(1+x)2=49 D.x+x(1+x)=49
【点拨】由题意,第一轮过后有(x+1)个人,第二轮又传染了x(x+1)个人,根据经过两轮传染后,共49人患流感,列出方程即可.
【解析】解:∵某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,
∴(x+1)+x(x+1)=49,
即:(1+x)2=49;
故选:C.
【点睛】本题考查由实际问题抽象出一元二次方程.找准等量关系,正确的列式,是解题的关键.
2.某地积极宣传和推广“吃农家饭,品农家菜,干农家活”乡村体验式旅游项目,去年该地旅游产业获利50万元,若计划明年旅游产业获利72万元,那么该地这两年旅游产业获利的年平均增长率应为( )
A.44% B.14.4% C.20% D.10%
【点拨】根据平均增长率的意义列式计算即可.
【解析】解:根据题意,得50(1+x)2=72,
解得x=0.2,x=﹣2.2(舍去),
故选:C.
【点睛】本题考查了一元二次方程的应用,熟练掌握平均增长率问题是解题的关键.
3.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,求每个支干长出多少小分支.设每个支干长出x小分支,那么根据题意可以列方程为( )
A.1+x+x2=91 B.1+x+x(1+x)=91 C.1+x+(1+x)2=91 D.1+(1+x)+(1+x)2=91
【点拨】如果设每个支干分出x个小分支,根据“每个支干又长出同样数目的小分支”可知:支干的数量为x个,小分支的数量为x x=x2个,然后根据主干、支干和小分支的总数是91就可以列出方程.
【解析】解:依题意得支干的数量为x个,小分支的数量为x x=x2个,
那么根据小分支,主干、支干和小分支的总数是91可列出方程为:1+x+x2=91.
故选:A.
【点睛】本题考查从实际问题抽象出一元二次方程,找出等量关系是解答本题的关键.
4.现将一张照片【长14英寸,宽10英寸】贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同均为a英寸,如图所示.已知矩形衬纸的面积为照片面积的2倍,则下列所列方程正确的是( )
A.2(10+a)(14+a)=14×10 B.2(10+2a)(14+2a)=14×10
C.(10+a)(14+a)=2×14×10 D.(10+2a)(14+2a)=2×14×10
【点拨】根据关键语句“矩形衬纸的面积为照片面积的2倍”列出方程求解即可.
【解析】解:依题意,矩形衬纸的面积为(10+2a)(14+2a),
照片面积为14×10,
所以(10+2a)(14+2a)=2×14×10,
故选:D.
【点睛】本题考查了由实际问题抽象出一元二次方程的知识,解题的关键是表示出大矩形的长与宽.根据“矩形衬纸的面积为照片面积的2倍”进行列式,即可作答.
5.某校自启动“书香校园 悦读成长”工程以来,成效显著,形成人人爱读书的良好氛围.该校图书馆三月份借出图书490本,五月份借出图书810本,设这两个月借出的图书平均每月增长率为x,则下列列出的方程正确的是( )
A.810(1﹣x)2=490 B.490(1+x)2=810 C.810(1﹣2x)=490 D.490(1+2x)=810
【点拨】首先表示出四月份借出图书490(1+x)本,五月份借出图书490(1+x)2本,然后根据四、五月份共借出图书本列出方程即可.
【解析】解:根据题意得:490(1+x)2=810,
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,解决本题的关键是得到相应的等量关系,注意四、五月份借出图书量是在三月份借出图书量的基础上得到的.
6.某地足球联赛中,参赛的每两个队之间都需要进行一场比赛,共比赛了45场.设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x+1)=45 B. C.x(x﹣1)=45 D.
【点拨】根据参赛的每两个队之间都需要进行一场比赛,共比赛了45场.设共有x个队参加比赛,则列式,即可作答.
【解析】解:设共有x个队参加比赛,依据参赛的每两个队之间都需要进行一场比赛,共比赛了45场,得得:
,
故选:D.
【点睛】本题考查了一元二次方程的应用,解答本题的关键是找准等量关系,列出一元二次方程.
7.某商店原来每天可销售某种水果100kg,每千克盈利7元,为了减少库存,经市场调查,如果这种水果每千克降价1元,那么每天可多售出30kg,若要每天盈利800元,则每千克应降价多少元?设每千克应降价x元,则所列方程是( )
A.(100+x)(7+x)=800 B.(100+30x)(7﹣x)=800
C.(100+30x)(7+x)=800 D.(100+x)(7﹣30x)=800
【点拨】当每千克降价x元时,每千克的销售利润为(7﹣x)元,每天可售出(100+30x)千克,利用总利润=每千克的销售利润×日销售量,即可列出关于x的一元二次方程,此题得解.
【解析】解:当每千克降价x元时,每千克的销售利润为(7﹣x)元,每天可售出(100+30x)千克.
根据题意得:(100+30x)(7﹣x)=800.
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
8.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.设动点P运动时间为t(t>0),当PQ=BC时,则t的值为 10s .
【点拨】当运动时间为t(t>0)时,CP=2t cm,CQ=|25﹣t|cm,利用勾股定理,结合PQ=BC,可列出关于t的一元二次方程,解之取其符合题意的值,即可得出结论.
【解析】解:当运动时间为t(t>0)时,CP=2t cm,CQ=|25﹣t|cm,
根据题意得:PQ2=CP2+CQ2,
即252=(2t)2+(25﹣t)2,
整理得:t2﹣10t=0,
解得:t1=0(不符合题意,舍去),t2=10,
∴t的值为10s.
故答案为:10s.
【点睛】本题考查了一元二次方程的应用以及勾股定理,找准等量关系,正确列出一元二次方程是解题的关键.
9.一个两位数,个位数字与十位数字之和是5,十位数字与个位数字对调后所得的数与原数相乘,得736,这个两位数是 23或32 .
【点拨】设原数的个位数字是x,则十位数字是5﹣x,然后根据等量关系“个位数字与十位数字对调后所得新数比原数小9”列一元二次方程求解即可.
【解析】解:设原数的个位数字是x,则十位数字是5﹣x.
根据题意得:[10(5﹣x)+x][10x+(5﹣x)]=736,
整理得,81x2﹣405x+486=0,
解得x=2或x=3,
所以5﹣x=5﹣2=3或5﹣x=5﹣3=2.
所以这个两位数是23或32.
故答案为:23或32.
【点睛】本题主要考查一元二次方程的应用,关键是根据题意找到等量关系式.
10.国庆期间,某博物馆展出的珍贵文物吸引了众多游客.通过这些文物,人们仿佛穿越时空,与历史对话,这不仅丰富了精神生活,也促进了文化的传承与发展.据统计,博物馆10月1日接待的人数比9月30日的2倍多0.2万人,这两天共接待2.9万人.
(1)求博物馆10月1日接待游客的人数;
(2)10月2日、3日游客继续增加,据统计10月3日接待游客2.88万人,预计10月4日游客数量将达到高峰.为使游客有较好的体验效果,规定人数达到3.5万人时,将会采取临时限流措施.按10月2日、3日的日平均增长率计算,10月4日是否需要临时限流?
【点拨】(1)设博物馆9月30日接待游客x万人,则博物馆10月1日接待游客(2x+0.2)万人,根据这两天共接待2.9万人,可列出关于x的一元一次方程,解之可得出x的值,再将其代入(2x+0.2)中,即可求出结论;
(2)设10月2日、3日的日平均增长率为y,利用10月3日接待游客数量=10月1日接待游客数量×(1+10月2日、3日的日平均增长率)2,可列出关于y的一元二次方程,解之可得出y的值,将其符合题意的值代入2.88(1+y)中,可求出预计10月4日接待游客数量,再将其与3.5万人比较后,即可得出结论.
【解析】解:(1)设博物馆9月30日接待游客x万人,则博物馆10月1日接待游客(2x+0.2)万人,
根据题意得:x+(2x+0.2)=2.9,
解得:x=0.9,
∴2x+0.2=2×0.9+0.2=2(万人).
答:博物馆10月1日接待游客2万人;
(2)设10月2日、3日的日平均增长率为y,
根据题意得:2(1+y)2=2.88,
解得:y1=0.2=20%,y2=﹣2.2(不符合题意,舍去),
∴2.88(1+y)=2.88×(1+20%)=3.456(万人),
∵3.456<3.5,
∴按10月2日、3日的日平均增长率计算,10月4日不需要临时限流.
【点睛】本题考查了一元一次方程的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)找准等量关系,正确列出一元二次方程.
11.随着科技的不断进步,人工智能(AI)正逐渐渗透到我们的生活和工作.从家庭助手到自动驾驶汽车,再到智能医疗,AI的应用前景广阔且充满无限可能.某人工智能科技体验馆在十一假期间为学生们制订了丰富多彩的体验活动,团体票收费标准为:如果人数不超过10人,人均费用为240元;如果人数超过10人,每增加1人,人均费用降低5元,但人均旅游费用不得低于170元.
(1)若有14人参加旅游,人均费用是 220 元.
(2)某兴趣小组的学生们去参加体验活动,团体票的费用共3600元,求参加活动的学生人数.
【点拨】(1)由题意列式计算即可;
(2)设参加活动的学生人数为x人,根据团体票的费用共3600元,列出一元二次方程,解之取符合题意的值即可.
【解析】解:(1)由题意得:240﹣(14﹣10)×5=240﹣20=220,
即若有14人参加旅游,人均费用是22元,
故答案为:220;
(2)设参加活动的学生人数为x人,
由题意得:x[240﹣5(x﹣10)]=3600,
整理得:x2﹣58x+720=0,
解得:x1=18,x2=40,
当x1=18时,240﹣5×(18﹣10)=200>170,符合题意;
当x2=40时,240﹣5×(40﹣10)=90<170,不符合题意,舍去;
答:参加活动的学生人数为18人.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
12.如图,在一块长28m、宽10m的矩形草坪中修建小路,已知剩余草地的面积是243m2.设小路的宽度为x m,根据题意,下面所列方程正确的是( )
A.28×10﹣28x﹣10x=243 B.2(28﹣x+10﹣x)=243
C.(28﹣x)(10﹣x)+x2=243 D.(28﹣x)(10﹣x)=243
【点拨】设道路的宽x m,根据利用平移的性质得出草坪的面积=长为(28﹣x)m,宽为(10﹣x)m的长方形的面积,由长方形面积公式即可得出关于x的一元二次方程,此题得解.
【解析】解:在一块长28m、宽10m的矩形草坪中修建小路,已知剩余草地的面积是243m2.
设道路的宽x m,由题意可得:
(28﹣x)(10﹣x)=243.
故选:D.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
13.某农场要建一个饲养场(矩形ABCD),两面靠墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.
(1)若饲养场(矩形ABCD)的一边CD长为8米,则另一边BC= 24 米.
(2)若饲养场(矩形ABCD)的面积为180平方米,求边CD的长.
(3)饲养场的面积能达到210平方米吗?若能达到,求出边CD的长;若不能达到,请说明理由.
【点拨】(1)由木栏总长为45米,即可求出BC的长;
(2)设CD=x(0<x≤15)米,则BC=(48﹣3x)米,根据饲养场(矩形ABCD)的面积为180平方米,即可得出关于x的一元二次方程,解之即可得出x的值,再结合AD位置的墙最大可用长度为27米(AD=BC),即可确定结论;
(3)设CD=y(0<y≤15)米,则BC=(48﹣3y)米,根据饲养场(矩形ABCD)的面积为210平方米,即可得出关于y的一元二次方程,由根的判别式Δ=﹣24<0,即可得出饲养场的面积不能达到210平方米.
【解析】解:(1)BC=45﹣8﹣2×(8﹣1)+1=24(米).
故答案为:24.
(2)设CD=x(0<x≤15)米,则BC=45﹣x﹣2(x﹣1)+1=(48﹣3x)米,
依题意得:x(48﹣3x)=180,
整理得:x2﹣16x+60=0,
解得:x1=6,x2=10.
当x=6时,48﹣3x=48﹣3×6=30(米),30>27,不合题意,舍去;
当x=10时,48﹣3x=48﹣3×10=18(米),符合题意.
答:边CD的长为10米.
(3)不能,理由如下:
设CD=y(0<y≤15)米,则BC=45﹣y﹣2(y﹣1)+1=(48﹣3y)米,
依题意得:y(48﹣3y)=210,
整理得:y2﹣16y+70=0.
∵Δ=(﹣16)2﹣4×1×70=256﹣280=﹣24<0,
∴该方程没有实数根,
∴饲养场的面积不能达到210平方米.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
14.“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2022年的20万人增加到2024年的33.8万人.
(1)求该市2023,2024这两年参加健身运动人数的年均增长率.
(2)某网店以每组30元的进价购进一批哑铃组.当每组售价为50元时,12月份售出了150组,随着市民健身热情的增加,该网店的哑铃组十分畅销.为了回馈顾客,该网店决定从1月份起采用降价促销的方式.经调查发现,该哑铃组每组每降价1元,销售量就增加10组,该网店计划1月份售卖哑铃组获利3060元,为了尽可能多的让利于顾客,该哑铃组每组应降价多少元?
【点拨】(1)设该市2023,2024这两年参加健身运动人数的年均增长率为x,根据从2022年的20万人增加到2024年的33.8万人,列出一元二次方程,解之取其符合题意的值即可;
(2)设该哑铃组每组应降价m元,则1月份销售量为(150+10m)组,根据该网店计划1月份售卖哑铃组获利3060元,列出一元二次方程,解之取其符合题意的值即可.
【解析】解:(1)设该市2023,2024这两年参加健身运动人数的年均增长率为x,
由题意得:20(1+x)2=33.8,
解得:x1=0.3=30%,x2=﹣2.3(不符合题意,舍去),
答:该市2023,2024这两年参加健身运动人数的年均增长率为30%;
(2)设该哑铃组每组应降价m元,则1月份销售量为(150+10m)组,
由题意得:(50﹣m﹣30)(150+10m)=3060,
整理得:m2﹣5m+6=0,
解得:m1=2(不符合题意,舍去),m2=3,
答:该哑铃组每组应降价3元.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
15.根据以下销售情况,解决销售任务.
销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,它们的销售情况如下:
店面 甲店 乙店
日销售情况 每天可售出20件,每件盈利40元. 每天可售出32件,每件盈利30元.
市场调查 经调查发现,每件衬衫每降价1元,甲、乙两家店一天都可多售出2件.
情况设置 设甲店每件衬衫降价a元,乙店每件衬衫降价b元.
任务解决
任务1 甲店每天的销售量 (20+2a)件 (用含a的代数式表示).乙店每天的销售量 (32+2b)件 (用含b的代数式表示).
任务2 当a=5,b=4时,分别求出甲、乙店每天的盈利.
任务3 总公司规定两家分店下降的价格必须相同,请求出每件衬衫下降多少元时,两家分店一天的盈利和为2244元.
【点拨】任务1,由题意即可得出结论;
任务2:,由盈利=每件盈利×销售量,分别列式计算即可;
任务3,设每件衬衫下降m元时,两家分店一天的盈利和为2244元,列出一元二次方程,解方程即可.
【解析】解:任务1,甲店每天的销售量为(20+2a)件,乙店每天的销售量为(32+2b)件,
故答案为:(20+2a)件,(32+2b)件;
任务2,当a=5时,甲店每天的盈利为(40﹣5)×(20+2×5)=1050(元);
当b=4时,乙店每天的盈利为(30﹣4)×(32+2×4)=1040(元);
任务3,设每件衬衫下降m元时,两家分店一天的盈利和为2244元,
由题意得:(40﹣m)(20+2m)+(30﹣m)(32+2m)=2244,
整理得:m2﹣22m+121=0,
解得:m1=m2=11,
即每件衬衫下降11元时,两家分店一天的盈利和为2244元.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
16.在矩形ABCD中,AB=10cm,BC=12cm,点P从点A开始沿边AB向终点B以2cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以4cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒(t>0).
(1)当t为何值时,PQ的长度等于10cm?
(2)是否存在t的值,使得五边形APQCD的面积等于104cm2?若存在,请求出此时t的值;若不存在,请说明理由.
【点拨】(1)由题意可知AP=2t cm,BQ=4t cm,则PB=AB﹣AP=(10﹣2t)cm,在Rt△PBQ中,由勾股定理得出方程,解之取符合题意的值即可;
(2)根据五边形APQCD的面积等于104cm2,列出一元二次方程,解之取符合题意的值即可.
【解析】解:(1)由题意得:AP=2t cm,BQ=4t cm,则PB=AB﹣AP=(10﹣2t)cm,
在Rt△PBQ中,由勾股定理得:PB2+BQ2=PQ2,
即(10﹣2t)2+(4t)2=102,
整理得:t2﹣2t=0,
解得:t1=2,t2=0(不合题意,舍去),
∴当t=2时,PQ的长度等于10cm;
(2)存在t的值,使得五边形APQCD的面积等于104cm2,理由如下:
由题意得:S长方形ABCD=10×12=120(cm2),
S△PBQ=PB BP=×(10﹣2t)×4t=﹣4t2+20t,
∴S五边形APQCD=S长方形ABCD﹣S△PBQ=120﹣(﹣4t2+20t)=104,
整理得:t2﹣5t+4=0,
解得:t1=4,t2=1,
当t=4时,BQ=16cm>12cm,不合题意,舍去;
当t=1时,BQ=4cm<12cm,符合题意;
∴存在t的值,使得五边形APQCD的面积等于104cm2,此时t的值为1.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
17.布置某艺术中心的会场时,工作人员准备利用35米长的地为一边,用68米隔栏绳围另三边,设立一个面积为600平方米的长方形等候区,如图,为了方便群众进出,在两边各空出一个1米的出入口(出入口不用隔栏绳).如果设这个长方形垂直于墙的一边长为x米,那么可以列出关于x的方程( )
A.(68+2﹣2x) (x﹣1)=600 B.(68﹣2﹣2x) (x﹣1)=600
C.(68+2﹣2x)x=600 D.(68﹣2﹣2x)x=600
【点拨】利用矩形面积为600,构建方程即可.
【解析】解:由题意,x(68﹣2﹣2x)=600.
故选:D.
【点睛】本题考查由实际问题抽象出一元二次方程,解题的关键是理解题意,正确寻找等量关系构建方程.
18.清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
【点拨】先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,利用大正方形的面积=阴影部分的面积+4×小正方形的面积,可得出大正方形的面积,再利用该方程的正数解=大正方形的边长﹣2×小正方形的边长,即可得出结论.
【解析】解:先构造一个面积为y2的正方形,再以该正方形的边长为一边向外构造四个面积均为5y的矩形,
∵阴影部分的面积为156,
∴y2+4×5y=y2+20y=156,
∴大正方形的面积=156+4×52=256,
∴大正方形的边长==16,
∴方程y2+20y+m=0的正数解为16﹣2×5=16﹣10=6,
故选:A.
【点睛】本题考查了一元二次方程的应用,模仿案例,构造出符合题意的大正方形是解题的关键.
19.定义新运算:,例如:﹣2 4=(﹣2)2﹣4=0,2 3=﹣2+3=1.若,则x的值为 或 .
【点拨】根据新定义运算法则列出方程求解即可.
【解析】解:∵,
而,
∴①当x≤0时,则有,
解得,;
②当x>0时,,
解得,,
综上所述,x的值是或,
故答案为:或.
【点睛】本题考查了一元二次方程的应用,一元一次方程的应用,解题的关键是根据题意找到等量关系式.
20.利用图形分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是长方形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=6,b=3,则长方形ABCD的面积是 36 .
【点拨】设小正方形的边长为x,利用a、b、x表示矩形的面积,再用a、b、x表示三角形以及正方形的面积,根据面积列出关于a、b、x的关系式,解出x,即可求出矩形面积.
【解析】解:设小正方形的边长为x,
∴矩形的长为(a+x),宽为(b+x),
由图1可得:,
整理得:x2+ax+bx﹣ab=0,
∵a=6,b=3,
∴x2+9x﹣18=0,
∴x2+9x=18,
∴矩形的面积为(a+x)(b+x)=(x+6)(x+3)=x2+9x+18=18+18=36.
故答案为:36.
【点睛】本题考查了一元二次方程的运用,解题的关键是构建方程解决问题.
21.根据以下素材,探索完成任务.
背景素材
素材1 随着数字技术、新能源、新材料等不断突破,我国创造业发展迎来重大机遇,天府科技园工作实验室借助智能化,对某款电动车的零部件进行一体化加工,以相同的生产效率提升,该零件7月份生产500个,9月份生产720个.
素材2 该园工作实验室的零部件成本为30元/个,销售一段时间后发现,当零部件售价为50元/个时,月销售量为800个,若在此基础上售价每下降2元,则月销售量将增加20个.为刺激经济的快速增长,政府给予实验室支持,当销量不低于900个时,每个将有5元的科技创新补贴.
问题解决
任务1 工作实验室从7月份到9月份生产数量的平均增长率;
任务2 使工作实验室月销售利润达到13500元,而且尽可能让车企得到实惠,社会普及增加,则该零件的实际售价应定为多少元?
【点拨】任务1:设工作实验室从7月份到9月份生产数量的平均增长率为x,利用9月份生产数量=7月份生产数量×(1+工作实验室从7月份到9月份生产数量的平均增长率)2,可列出关于x的一元二次方程,解之取其符合题意的值,即可得出结论;
任务2:设该零件的实际售价定为y元,分y>40及y≤40两种情况考虑,利用总利润=每个的销售利润×月销售量,可列出关于y的一元二次方程,解之可得出y的值,再结合“要尽可能让车企得到实惠,社会普及增加”,即可确定结论.
【解析】解:任务1:设工作实验室从7月份到9月份生产数量的平均增长率为x,
根据题意得:500(1+x)2=720,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去).
答:工作实验室从7月份到9月份生产数量的平均增长率为20%;
任务2:设该零件的实际售价定为y元,
当y>40时,每个零件的销售利润为(y﹣30)元,月销售量为800+×20=(1300﹣10y)个,
根据题意得:(y﹣30)(1300﹣10y)=13500,
整理得:y2﹣160y+5250=0,
解得:y1=80﹣5,y2=80+5(不符合题意,舍去);
当y≤40时,每个零件的销售利润为(y﹣30+5)元,月销售量为(1300﹣10y)个,
根据题意得:(y﹣30+5)(1300﹣10y)=13500,
整理得:y2﹣155y+4600=0,
解得:y3=40,y4=115(不符合题意,舍去).
又∵要尽可能让车企得到实惠,社会普及增加,
∴y=40.
答:该零件的实际售价应定为40元.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2.3 一元二次方程的应用 同步分层作业
1.春季是流感的高发时期,某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,则可列方程( )
A.1+x+x2=49 B.x+x2=49 C.(1+x)2=49 D.x+x(1+x)=49
2.某地积极宣传和推广“吃农家饭,品农家菜,干农家活”乡村体验式旅游项目,去年该地旅游产业获利50万元,若计划明年旅游产业获利72万元,那么该地这两年旅游产业获利的年平均增长率应为( )
A.44% B.14.4% C.20% D.10%
3.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,求每个支干长出多少小分支.设每个支干长出x小分支,那么根据题意可以列方程为( )
A.1+x+x2=91 B.1+x+x(1+x)=91 C.1+x+(1+x)2=91 D.1+(1+x)+(1+x)2=91
4.现将一张照片【长14英寸,宽10英寸】贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同均为a英寸,如图所示.已知矩形衬纸的面积为照片面积的2倍,则下列所列方程正确的是( )
A.2(10+a)(14+a)=14×10 B.2(10+2a)(14+2a)=14×10
C.(10+a)(14+a)=2×14×10 D.(10+2a)(14+2a)=2×14×10
5.某校自启动“书香校园 悦读成长”工程以来,成效显著,形成人人爱读书的良好氛围.该校图书馆三月份借出图书490本,五月份借出图书810本,设这两个月借出的图书平均每月增长率为x,则下列列出的方程正确的是( )
A.810(1﹣x)2=490 B.490(1+x)2=810 C.810(1﹣2x)=490 D.490(1+2x)=810
6.某地足球联赛中,参赛的每两个队之间都需要进行一场比赛,共比赛了45场.设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x+1)=45 B. C.x(x﹣1)=45 D.
7.某商店原来每天可销售某种水果100kg,每千克盈利7元,为了减少库存,经市场调查,如果这种水果每千克降价1元,那么每天可多售出30kg,若要每天盈利800元,则每千克应降价多少元?设每千克应降价x元,则所列方程是( )
A.(100+x)(7+x)=800 B.(100+30x)(7﹣x)=800
C.(100+30x)(7+x)=800 D.(100+x)(7﹣30x)=800
8.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.设动点P运动时间为t(t>0),当PQ=BC时,则t的值为 .
9.一个两位数,个位数字与十位数字之和是5,十位数字与个位数字对调后所得的数与原数相乘,得736,这个两位数是 .
10.国庆期间,某博物馆展出的珍贵文物吸引了众多游客.通过这些文物,人们仿佛穿越时空,与历史对话,这不仅丰富了精神生活,也促进了文化的传承与发展.据统计,博物馆10月1日接待的人数比9月30日的2倍多0.2万人,这两天共接待2.9万人.
(1)求博物馆10月1日接待游客的人数;
(2)10月2日、3日游客继续增加,据统计10月3日接待游客2.88万人,预计10月4日游客数量将达到高峰.为使游客有较好的体验效果,规定人数达到3.5万人时,将会采取临时限流措施.按10月2日、3日的日平均增长率计算,10月4日是否需要临时限流?
11.随着科技的不断进步,人工智能(AI)正逐渐渗透到我们的生活和工作.从家庭助手到自动驾驶汽车,再到智能医疗,AI的应用前景广阔且充满无限可能.某人工智能科技体验馆在十一假期间为学生们制订了丰富多彩的体验活动,团体票收费标准为:如果人数不超过10人,人均费用为240元;如果人数超过10人,每增加1人,人均费用降低5元,但人均旅游费用不得低于170元.
(1)若有14人参加旅游,人均费用是 元.
(2)某兴趣小组的学生们去参加体验活动,团体票的费用共3600元,求参加活动的学生人数.
12.如图,在一块长28m、宽10m的矩形草坪中修建小路,已知剩余草地的面积是243m2.设小路的宽度为x m,根据题意,下面所列方程正确的是( )
A.28×10﹣28x﹣10x=243 B.2(28﹣x+10﹣x)=243
C.(28﹣x)(10﹣x)+x2=243 D.(28﹣x)(10﹣x)=243
13.某农场要建一个饲养场(矩形ABCD),两面靠墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.
(1)若饲养场(矩形ABCD)的一边CD长为8米,则另一边BC= 米.
(2)若饲养场(矩形ABCD)的面积为180平方米,求边CD的长.
(3)饲养场的面积能达到210平方米吗?若能达到,求出边CD的长;若不能达到,请说明理由.
14.“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2022年的20万人增加到2024年的33.8万人.
(1)求该市2023,2024这两年参加健身运动人数的年均增长率.
(2)某网店以每组30元的进价购进一批哑铃组.当每组售价为50元时,12月份售出了150组,随着市民健身热情的增加,该网店的哑铃组十分畅销.为了回馈顾客,该网店决定从1月份起采用降价促销的方式.经调查发现,该哑铃组每组每降价1元,销售量就增加10组,该网店计划1月份售卖哑铃组获利3060元,为了尽可能多的让利于顾客,该哑铃组每组应降价多少元?
15.根据以下销售情况,解决销售任务.
销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,它们的销售情况如下:
店面 甲店 乙店
日销售情况 每天可售出20件,每件盈利40元. 每天可售出32件,每件盈利30元.
市场调查 经调查发现,每件衬衫每降价1元,甲、乙两家店一天都可多售出2件.
情况设置 设甲店每件衬衫降价a元,乙店每件衬衫降价b元.
任务解决
任务1 甲店每天的销售量 (用含a的代数式表示).乙店每天的销售量 (用含b的代数式表示).
任务2 当a=5,b=4时,分别求出甲、乙店每天的盈利.
任务3 总公司规定两家分店下降的价格必须相同,请求出每件衬衫下降多少元时,两家分店一天的盈利和为2244元.
16.在矩形ABCD中,AB=10cm,BC=12cm,点P从点A开始沿边AB向终点B以2cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以4cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒(t>0).
(1)当t为何值时,PQ的长度等于10cm?
(2)是否存在t的值,使得五边形APQCD的面积等于104cm2?若存在,请求出此时t的值;若不存在,请说明理由.
17.布置某艺术中心的会场时,工作人员准备利用35米长的地为一边,用68米隔栏绳围另三边,设立一个面积为600平方米的长方形等候区,如图,为了方便群众进出,在两边各空出一个1米的出入口(出入口不用隔栏绳).如果设这个长方形垂直于墙的一边长为x米,那么可以列出关于x的方程( )
A.(68+2﹣2x) (x﹣1)=600 B.(68﹣2﹣2x) (x﹣1)=600
C.(68+2﹣2x)x=600 D.(68﹣2﹣2x)x=600
18.清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
19.定义新运算:,例如:﹣2 4=(﹣2)2﹣4=0,2 3=﹣2+3=1.若,则x的值为 .
20.利用图形分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是长方形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=6,b=3,则长方形ABCD的面积是 .
21.根据以下素材,探索完成任务.
背景素材
素材1 随着数字技术、新能源、新材料等不断突破,我国创造业发展迎来重大机遇,天府科技园工作实验室借助智能化,对某款电动车的零部件进行一体化加工,以相同的生产效率提升,该零件7月份生产500个,9月份生产720个.
素材2 该园工作实验室的零部件成本为30元/个,销售一段时间后发现,当零部件售价为50元/个时,月销售量为800个,若在此基础上售价每下降2元,则月销售量将增加20个.为刺激经济的快速增长,政府给予实验室支持,当销量不低于900个时,每个将有5元的科技创新补贴.
问题解决
任务1 工作实验室从7月份到9月份生产数量的平均增长率;
任务2 使工作实验室月销售利润达到13500元,而且尽可能让车企得到实惠,社会普及增加,则该零件的实际售价应定为多少元?
答案与解析
1.春季是流感的高发时期,某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,则可列方程( )
A.1+x+x2=49 B.x+x2=49 C.(1+x)2=49 D.x+x(1+x)=49
【点拨】由题意,第一轮过后有(x+1)个人,第二轮又传染了x(x+1)个人,根据经过两轮传染后,共49人患流感,列出方程即可.
【解析】解:∵某校4月初有一人患了流感,经过两轮传染后,共49人患流感,假设每轮传染中平均每人传染x人,
∴(x+1)+x(x+1)=49,
即:(1+x)2=49;
故选:C.
【点睛】本题考查由实际问题抽象出一元二次方程.找准等量关系,正确的列式,是解题的关键.
2.某地积极宣传和推广“吃农家饭,品农家菜,干农家活”乡村体验式旅游项目,去年该地旅游产业获利50万元,若计划明年旅游产业获利72万元,那么该地这两年旅游产业获利的年平均增长率应为( )
A.44% B.14.4% C.20% D.10%
【点拨】根据平均增长率的意义列式计算即可.
【解析】解:根据题意,得50(1+x)2=72,
解得x=0.2,x=﹣2.2(舍去),
故选:C.
【点睛】本题考查了一元二次方程的应用,熟练掌握平均增长率问题是解题的关键.
3.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,求每个支干长出多少小分支.设每个支干长出x小分支,那么根据题意可以列方程为( )
A.1+x+x2=91 B.1+x+x(1+x)=91 C.1+x+(1+x)2=91 D.1+(1+x)+(1+x)2=91
【点拨】如果设每个支干分出x个小分支,根据“每个支干又长出同样数目的小分支”可知:支干的数量为x个,小分支的数量为x x=x2个,然后根据主干、支干和小分支的总数是91就可以列出方程.
【解析】解:依题意得支干的数量为x个,小分支的数量为x x=x2个,
那么根据小分支,主干、支干和小分支的总数是91可列出方程为:1+x+x2=91.
故选:A.
【点睛】本题考查从实际问题抽象出一元二次方程,找出等量关系是解答本题的关键.
4.现将一张照片【长14英寸,宽10英寸】贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同均为a英寸,如图所示.已知矩形衬纸的面积为照片面积的2倍,则下列所列方程正确的是( )
A.2(10+a)(14+a)=14×10 B.2(10+2a)(14+2a)=14×10
C.(10+a)(14+a)=2×14×10 D.(10+2a)(14+2a)=2×14×10
【点拨】根据关键语句“矩形衬纸的面积为照片面积的2倍”列出方程求解即可.
【解析】解:依题意,矩形衬纸的面积为(10+2a)(14+2a),
照片面积为14×10,
所以(10+2a)(14+2a)=2×14×10,
故选:D.
【点睛】本题考查了由实际问题抽象出一元二次方程的知识,解题的关键是表示出大矩形的长与宽.根据“矩形衬纸的面积为照片面积的2倍”进行列式,即可作答.
5.某校自启动“书香校园 悦读成长”工程以来,成效显著,形成人人爱读书的良好氛围.该校图书馆三月份借出图书490本,五月份借出图书810本,设这两个月借出的图书平均每月增长率为x,则下列列出的方程正确的是( )
A.810(1﹣x)2=490 B.490(1+x)2=810 C.810(1﹣2x)=490 D.490(1+2x)=810
【点拨】首先表示出四月份借出图书490(1+x)本,五月份借出图书490(1+x)2本,然后根据四、五月份共借出图书本列出方程即可.
【解析】解:根据题意得:490(1+x)2=810,
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,解决本题的关键是得到相应的等量关系,注意四、五月份借出图书量是在三月份借出图书量的基础上得到的.
6.某地足球联赛中,参赛的每两个队之间都需要进行一场比赛,共比赛了45场.设共有x个队参加比赛,则下列方程符合题意的是( )
A.x(x+1)=45 B. C.x(x﹣1)=45 D.
【点拨】根据参赛的每两个队之间都需要进行一场比赛,共比赛了45场.设共有x个队参加比赛,则列式,即可作答.
【解析】解:设共有x个队参加比赛,依据参赛的每两个队之间都需要进行一场比赛,共比赛了45场,得得:
,
故选:D.
【点睛】本题考查了一元二次方程的应用,解答本题的关键是找准等量关系,列出一元二次方程.
7.某商店原来每天可销售某种水果100kg,每千克盈利7元,为了减少库存,经市场调查,如果这种水果每千克降价1元,那么每天可多售出30kg,若要每天盈利800元,则每千克应降价多少元?设每千克应降价x元,则所列方程是( )
A.(100+x)(7+x)=800 B.(100+30x)(7﹣x)=800
C.(100+30x)(7+x)=800 D.(100+x)(7﹣30x)=800
【点拨】当每千克降价x元时,每千克的销售利润为(7﹣x)元,每天可售出(100+30x)千克,利用总利润=每千克的销售利润×日销售量,即可列出关于x的一元二次方程,此题得解.
【解析】解:当每千克降价x元时,每千克的销售利润为(7﹣x)元,每天可售出(100+30x)千克.
根据题意得:(100+30x)(7﹣x)=800.
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
8.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.设动点P运动时间为t(t>0),当PQ=BC时,则t的值为 10s .
【点拨】当运动时间为t(t>0)时,CP=2t cm,CQ=|25﹣t|cm,利用勾股定理,结合PQ=BC,可列出关于t的一元二次方程,解之取其符合题意的值,即可得出结论.
【解析】解:当运动时间为t(t>0)时,CP=2t cm,CQ=|25﹣t|cm,
根据题意得:PQ2=CP2+CQ2,
即252=(2t)2+(25﹣t)2,
整理得:t2﹣10t=0,
解得:t1=0(不符合题意,舍去),t2=10,
∴t的值为10s.
故答案为:10s.
【点睛】本题考查了一元二次方程的应用以及勾股定理,找准等量关系,正确列出一元二次方程是解题的关键.
9.一个两位数,个位数字与十位数字之和是5,十位数字与个位数字对调后所得的数与原数相乘,得736,这个两位数是 23或32 .
【点拨】设原数的个位数字是x,则十位数字是5﹣x,然后根据等量关系“个位数字与十位数字对调后所得新数比原数小9”列一元二次方程求解即可.
【解析】解:设原数的个位数字是x,则十位数字是5﹣x.
根据题意得:[10(5﹣x)+x][10x+(5﹣x)]=736,
整理得,81x2﹣405x+486=0,
解得x=2或x=3,
所以5﹣x=5﹣2=3或5﹣x=5﹣3=2.
所以这个两位数是23或32.
故答案为:23或32.
【点睛】本题主要考查一元二次方程的应用,关键是根据题意找到等量关系式.
10.国庆期间,某博物馆展出的珍贵文物吸引了众多游客.通过这些文物,人们仿佛穿越时空,与历史对话,这不仅丰富了精神生活,也促进了文化的传承与发展.据统计,博物馆10月1日接待的人数比9月30日的2倍多0.2万人,这两天共接待2.9万人.
(1)求博物馆10月1日接待游客的人数;
(2)10月2日、3日游客继续增加,据统计10月3日接待游客2.88万人,预计10月4日游客数量将达到高峰.为使游客有较好的体验效果,规定人数达到3.5万人时,将会采取临时限流措施.按10月2日、3日的日平均增长率计算,10月4日是否需要临时限流?
【点拨】(1)设博物馆9月30日接待游客x万人,则博物馆10月1日接待游客(2x+0.2)万人,根据这两天共接待2.9万人,可列出关于x的一元一次方程,解之可得出x的值,再将其代入(2x+0.2)中,即可求出结论;
(2)设10月2日、3日的日平均增长率为y,利用10月3日接待游客数量=10月1日接待游客数量×(1+10月2日、3日的日平均增长率)2,可列出关于y的一元二次方程,解之可得出y的值,将其符合题意的值代入2.88(1+y)中,可求出预计10月4日接待游客数量,再将其与3.5万人比较后,即可得出结论.
【解析】解:(1)设博物馆9月30日接待游客x万人,则博物馆10月1日接待游客(2x+0.2)万人,
根据题意得:x+(2x+0.2)=2.9,
解得:x=0.9,
∴2x+0.2=2×0.9+0.2=2(万人).
答:博物馆10月1日接待游客2万人;
(2)设10月2日、3日的日平均增长率为y,
根据题意得:2(1+y)2=2.88,
解得:y1=0.2=20%,y2=﹣2.2(不符合题意,舍去),
∴2.88(1+y)=2.88×(1+20%)=3.456(万人),
∵3.456<3.5,
∴按10月2日、3日的日平均增长率计算,10月4日不需要临时限流.
【点睛】本题考查了一元一次方程的应用以及一元二次方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)找准等量关系,正确列出一元二次方程.
11.随着科技的不断进步,人工智能(AI)正逐渐渗透到我们的生活和工作.从家庭助手到自动驾驶汽车,再到智能医疗,AI的应用前景广阔且充满无限可能.某人工智能科技体验馆在十一假期间为学生们制订了丰富多彩的体验活动,团体票收费标准为:如果人数不超过10人,人均费用为240元;如果人数超过10人,每增加1人,人均费用降低5元,但人均旅游费用不得低于170元.
(1)若有14人参加旅游,人均费用是 220 元.
(2)某兴趣小组的学生们去参加体验活动,团体票的费用共3600元,求参加活动的学生人数.
【点拨】(1)由题意列式计算即可;
(2)设参加活动的学生人数为x人,根据团体票的费用共3600元,列出一元二次方程,解之取符合题意的值即可.
【解析】解:(1)由题意得:240﹣(14﹣10)×5=240﹣20=220,
即若有14人参加旅游,人均费用是22元,
故答案为:220;
(2)设参加活动的学生人数为x人,
由题意得:x[240﹣5(x﹣10)]=3600,
整理得:x2﹣58x+720=0,
解得:x1=18,x2=40,
当x1=18时,240﹣5×(18﹣10)=200>170,符合题意;
当x2=40时,240﹣5×(40﹣10)=90<170,不符合题意,舍去;
答:参加活动的学生人数为18人.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
12.如图,在一块长28m、宽10m的矩形草坪中修建小路,已知剩余草地的面积是243m2.设小路的宽度为x m,根据题意,下面所列方程正确的是( )
A.28×10﹣28x﹣10x=243 B.2(28﹣x+10﹣x)=243
C.(28﹣x)(10﹣x)+x2=243 D.(28﹣x)(10﹣x)=243
【点拨】设道路的宽x m,根据利用平移的性质得出草坪的面积=长为(28﹣x)m,宽为(10﹣x)m的长方形的面积,由长方形面积公式即可得出关于x的一元二次方程,此题得解.
【解析】解:在一块长28m、宽10m的矩形草坪中修建小路,已知剩余草地的面积是243m2.
设道路的宽x m,由题意可得:
(28﹣x)(10﹣x)=243.
故选:D.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
13.某农场要建一个饲养场(矩形ABCD),两面靠墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.
(1)若饲养场(矩形ABCD)的一边CD长为8米,则另一边BC= 24 米.
(2)若饲养场(矩形ABCD)的面积为180平方米,求边CD的长.
(3)饲养场的面积能达到210平方米吗?若能达到,求出边CD的长;若不能达到,请说明理由.
【点拨】(1)由木栏总长为45米,即可求出BC的长;
(2)设CD=x(0<x≤15)米,则BC=(48﹣3x)米,根据饲养场(矩形ABCD)的面积为180平方米,即可得出关于x的一元二次方程,解之即可得出x的值,再结合AD位置的墙最大可用长度为27米(AD=BC),即可确定结论;
(3)设CD=y(0<y≤15)米,则BC=(48﹣3y)米,根据饲养场(矩形ABCD)的面积为210平方米,即可得出关于y的一元二次方程,由根的判别式Δ=﹣24<0,即可得出饲养场的面积不能达到210平方米.
【解析】解:(1)BC=45﹣8﹣2×(8﹣1)+1=24(米).
故答案为:24.
(2)设CD=x(0<x≤15)米,则BC=45﹣x﹣2(x﹣1)+1=(48﹣3x)米,
依题意得:x(48﹣3x)=180,
整理得:x2﹣16x+60=0,
解得:x1=6,x2=10.
当x=6时,48﹣3x=48﹣3×6=30(米),30>27,不合题意,舍去;
当x=10时,48﹣3x=48﹣3×10=18(米),符合题意.
答:边CD的长为10米.
(3)不能,理由如下:
设CD=y(0<y≤15)米,则BC=45﹣y﹣2(y﹣1)+1=(48﹣3y)米,
依题意得:y(48﹣3y)=210,
整理得:y2﹣16y+70=0.
∵Δ=(﹣16)2﹣4×1×70=256﹣280=﹣24<0,
∴该方程没有实数根,
∴饲养场的面积不能达到210平方米.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
14.“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2022年的20万人增加到2024年的33.8万人.
(1)求该市2023,2024这两年参加健身运动人数的年均增长率.
(2)某网店以每组30元的进价购进一批哑铃组.当每组售价为50元时,12月份售出了150组,随着市民健身热情的增加,该网店的哑铃组十分畅销.为了回馈顾客,该网店决定从1月份起采用降价促销的方式.经调查发现,该哑铃组每组每降价1元,销售量就增加10组,该网店计划1月份售卖哑铃组获利3060元,为了尽可能多的让利于顾客,该哑铃组每组应降价多少元?
【点拨】(1)设该市2023,2024这两年参加健身运动人数的年均增长率为x,根据从2022年的20万人增加到2024年的33.8万人,列出一元二次方程,解之取其符合题意的值即可;
(2)设该哑铃组每组应降价m元,则1月份销售量为(150+10m)组,根据该网店计划1月份售卖哑铃组获利3060元,列出一元二次方程,解之取其符合题意的值即可.
【解析】解:(1)设该市2023,2024这两年参加健身运动人数的年均增长率为x,
由题意得:20(1+x)2=33.8,
解得:x1=0.3=30%,x2=﹣2.3(不符合题意,舍去),
答:该市2023,2024这两年参加健身运动人数的年均增长率为30%;
(2)设该哑铃组每组应降价m元,则1月份销售量为(150+10m)组,
由题意得:(50﹣m﹣30)(150+10m)=3060,
整理得:m2﹣5m+6=0,
解得:m1=2(不符合题意,舍去),m2=3,
答:该哑铃组每组应降价3元.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
15.根据以下销售情况,解决销售任务.
销售情况分析
总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,它们的销售情况如下:
店面 甲店 乙店
日销售情况 每天可售出20件,每件盈利40元. 每天可售出32件,每件盈利30元.
市场调查 经调查发现,每件衬衫每降价1元,甲、乙两家店一天都可多售出2件.
情况设置 设甲店每件衬衫降价a元,乙店每件衬衫降价b元.
任务解决
任务1 甲店每天的销售量 (20+2a)件 (用含a的代数式表示).乙店每天的销售量 (32+2b)件 (用含b的代数式表示).
任务2 当a=5,b=4时,分别求出甲、乙店每天的盈利.
任务3 总公司规定两家分店下降的价格必须相同,请求出每件衬衫下降多少元时,两家分店一天的盈利和为2244元.
【点拨】任务1,由题意即可得出结论;
任务2:,由盈利=每件盈利×销售量,分别列式计算即可;
任务3,设每件衬衫下降m元时,两家分店一天的盈利和为2244元,列出一元二次方程,解方程即可.
【解析】解:任务1,甲店每天的销售量为(20+2a)件,乙店每天的销售量为(32+2b)件,
故答案为:(20+2a)件,(32+2b)件;
任务2,当a=5时,甲店每天的盈利为(40﹣5)×(20+2×5)=1050(元);
当b=4时,乙店每天的盈利为(30﹣4)×(32+2×4)=1040(元);
任务3,设每件衬衫下降m元时,两家分店一天的盈利和为2244元,
由题意得:(40﹣m)(20+2m)+(30﹣m)(32+2m)=2244,
整理得:m2﹣22m+121=0,
解得:m1=m2=11,
即每件衬衫下降11元时,两家分店一天的盈利和为2244元.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
16.在矩形ABCD中,AB=10cm,BC=12cm,点P从点A开始沿边AB向终点B以2cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以4cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒(t>0).
(1)当t为何值时,PQ的长度等于10cm?
(2)是否存在t的值,使得五边形APQCD的面积等于104cm2?若存在,请求出此时t的值;若不存在,请说明理由.
【点拨】(1)由题意可知AP=2t cm,BQ=4t cm,则PB=AB﹣AP=(10﹣2t)cm,在Rt△PBQ中,由勾股定理得出方程,解之取符合题意的值即可;
(2)根据五边形APQCD的面积等于104cm2,列出一元二次方程,解之取符合题意的值即可.
【解析】解:(1)由题意得:AP=2t cm,BQ=4t cm,则PB=AB﹣AP=(10﹣2t)cm,
在Rt△PBQ中,由勾股定理得:PB2+BQ2=PQ2,
即(10﹣2t)2+(4t)2=102,
整理得:t2﹣2t=0,
解得:t1=2,t2=0(不合题意,舍去),
∴当t=2时,PQ的长度等于10cm;
(2)存在t的值,使得五边形APQCD的面积等于104cm2,理由如下:
由题意得:S长方形ABCD=10×12=120(cm2),
S△PBQ=PB BP=×(10﹣2t)×4t=﹣4t2+20t,
∴S五边形APQCD=S长方形ABCD﹣S△PBQ=120﹣(﹣4t2+20t)=104,
整理得:t2﹣5t+4=0,
解得:t1=4,t2=1,
当t=4时,BQ=16cm>12cm,不合题意,舍去;
当t=1时,BQ=4cm<12cm,符合题意;
∴存在t的值,使得五边形APQCD的面积等于104cm2,此时t的值为1.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
17.布置某艺术中心的会场时,工作人员准备利用35米长的地为一边,用68米隔栏绳围另三边,设立一个面积为600平方米的长方形等候区,如图,为了方便群众进出,在两边各空出一个1米的出入口(出入口不用隔栏绳).如果设这个长方形垂直于墙的一边长为x米,那么可以列出关于x的方程( )
A.(68+2﹣2x) (x﹣1)=600 B.(68﹣2﹣2x) (x﹣1)=600
C.(68+2﹣2x)x=600 D.(68﹣2﹣2x)x=600
【点拨】利用矩形面积为600,构建方程即可.
【解析】解:由题意,x(68﹣2﹣2x)=600.
故选:D.
【点睛】本题考查由实际问题抽象出一元二次方程,解题的关键是理解题意,正确寻找等量关系构建方程.
18.清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
【点拨】先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,利用大正方形的面积=阴影部分的面积+4×小正方形的面积,可得出大正方形的面积,再利用该方程的正数解=大正方形的边长﹣2×小正方形的边长,即可得出结论.
【解析】解:先构造一个面积为y2的正方形,再以该正方形的边长为一边向外构造四个面积均为5y的矩形,
∵阴影部分的面积为156,
∴y2+4×5y=y2+20y=156,
∴大正方形的面积=156+4×52=256,
∴大正方形的边长==16,
∴方程y2+20y+m=0的正数解为16﹣2×5=16﹣10=6,
故选:A.
【点睛】本题考查了一元二次方程的应用,模仿案例,构造出符合题意的大正方形是解题的关键.
19.定义新运算:,例如:﹣2 4=(﹣2)2﹣4=0,2 3=﹣2+3=1.若,则x的值为 或 .
【点拨】根据新定义运算法则列出方程求解即可.
【解析】解:∵,
而,
∴①当x≤0时,则有,
解得,;
②当x>0时,,
解得,,
综上所述,x的值是或,
故答案为:或.
【点睛】本题考查了一元二次方程的应用,一元一次方程的应用,解题的关键是根据题意找到等量关系式.
20.利用图形分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是长方形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=6,b=3,则长方形ABCD的面积是 36 .
【点拨】设小正方形的边长为x,利用a、b、x表示矩形的面积,再用a、b、x表示三角形以及正方形的面积,根据面积列出关于a、b、x的关系式,解出x,即可求出矩形面积.
【解析】解:设小正方形的边长为x,
∴矩形的长为(a+x),宽为(b+x),
由图1可得:,
整理得:x2+ax+bx﹣ab=0,
∵a=6,b=3,
∴x2+9x﹣18=0,
∴x2+9x=18,
∴矩形的面积为(a+x)(b+x)=(x+6)(x+3)=x2+9x+18=18+18=36.
故答案为:36.
【点睛】本题考查了一元二次方程的运用,解题的关键是构建方程解决问题.
21.根据以下素材,探索完成任务.
背景素材
素材1 随着数字技术、新能源、新材料等不断突破,我国创造业发展迎来重大机遇,天府科技园工作实验室借助智能化,对某款电动车的零部件进行一体化加工,以相同的生产效率提升,该零件7月份生产500个,9月份生产720个.
素材2 该园工作实验室的零部件成本为30元/个,销售一段时间后发现,当零部件售价为50元/个时,月销售量为800个,若在此基础上售价每下降2元,则月销售量将增加20个.为刺激经济的快速增长,政府给予实验室支持,当销量不低于900个时,每个将有5元的科技创新补贴.
问题解决
任务1 工作实验室从7月份到9月份生产数量的平均增长率;
任务2 使工作实验室月销售利润达到13500元,而且尽可能让车企得到实惠,社会普及增加,则该零件的实际售价应定为多少元?
【点拨】任务1:设工作实验室从7月份到9月份生产数量的平均增长率为x,利用9月份生产数量=7月份生产数量×(1+工作实验室从7月份到9月份生产数量的平均增长率)2,可列出关于x的一元二次方程,解之取其符合题意的值,即可得出结论;
任务2:设该零件的实际售价定为y元,分y>40及y≤40两种情况考虑,利用总利润=每个的销售利润×月销售量,可列出关于y的一元二次方程,解之可得出y的值,再结合“要尽可能让车企得到实惠,社会普及增加”,即可确定结论.
【解析】解:任务1:设工作实验室从7月份到9月份生产数量的平均增长率为x,
根据题意得:500(1+x)2=720,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去).
答:工作实验室从7月份到9月份生产数量的平均增长率为20%;
任务2:设该零件的实际售价定为y元,
当y>40时,每个零件的销售利润为(y﹣30)元,月销售量为800+×20=(1300﹣10y)个,
根据题意得:(y﹣30)(1300﹣10y)=13500,
整理得:y2﹣160y+5250=0,
解得:y1=80﹣5,y2=80+5(不符合题意,舍去);
当y≤40时,每个零件的销售利润为(y﹣30+5)元,月销售量为(1300﹣10y)个,
根据题意得:(y﹣30+5)(1300﹣10y)=13500,
整理得:y2﹣155y+4600=0,
解得:y3=40,y4=115(不符合题意,舍去).
又∵要尽可能让车企得到实惠,社会普及增加,
∴y=40.
答:该零件的实际售价应定为40元.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
