第三单元 统计 单元测试卷 沪教版四年级数学下册(含答案)
文档属性
| 名称 | 第三单元 统计 单元测试卷 沪教版四年级数学下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 793.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-28 00:00:00 | ||
图片预览



文档简介
第三单元 统计 单元测试卷
一、单选题
1.气象小组的同学要绘制一幅统计图公布上星期每天平均气温的变化情况,应选用( )统计图.
A.条形 B.折线 C.扇形
2.笑笑把2月12日到2月21日全国新冠肺炎患者治愈出院的人数制成了下面的折线统计图。
根据图中信息可以判断,下列描述错误的是( )。
A.在这十天中13日治愈出院的人数最少
B.这十天治愈出院人数都超过千人
C.这十天治愈出院的人数一直在不断上升
D.照这个趋势22日治愈出院的人数有可能会增加
3.下面的折线统计图,不可能表示的是( )
A.小胖连续6次的数学考试成绩 B.某地连续6天每日最高气温情况
C.超市上半年每月的营业总额 D.小明从1岁到6岁每年的身高
4.下列的表述中有( )句是正确的。
①在同一个平面内,过已知直线a外一点P,只能画1条与直线a平行的直线;
②在0.45和0.47之间只有一个小数是46,
③要反映小亚生病期间的体温变化情况,选择折线统计图比较合适;
④如果两条直线不平行,那么这两条直线一定互相垂直。
A.1 B.2 C.3 D.4
5.以下说法正确的是( )。
A.两个小数相乘,积一定小于 1
B.三角形和平行四边形都具有稳定性
C.0.30与0.300大小相等,计数单位也相同
D.统计深圳市今年1-6月共享单车月累计骑行次数变化情况,适合选用折线统计图
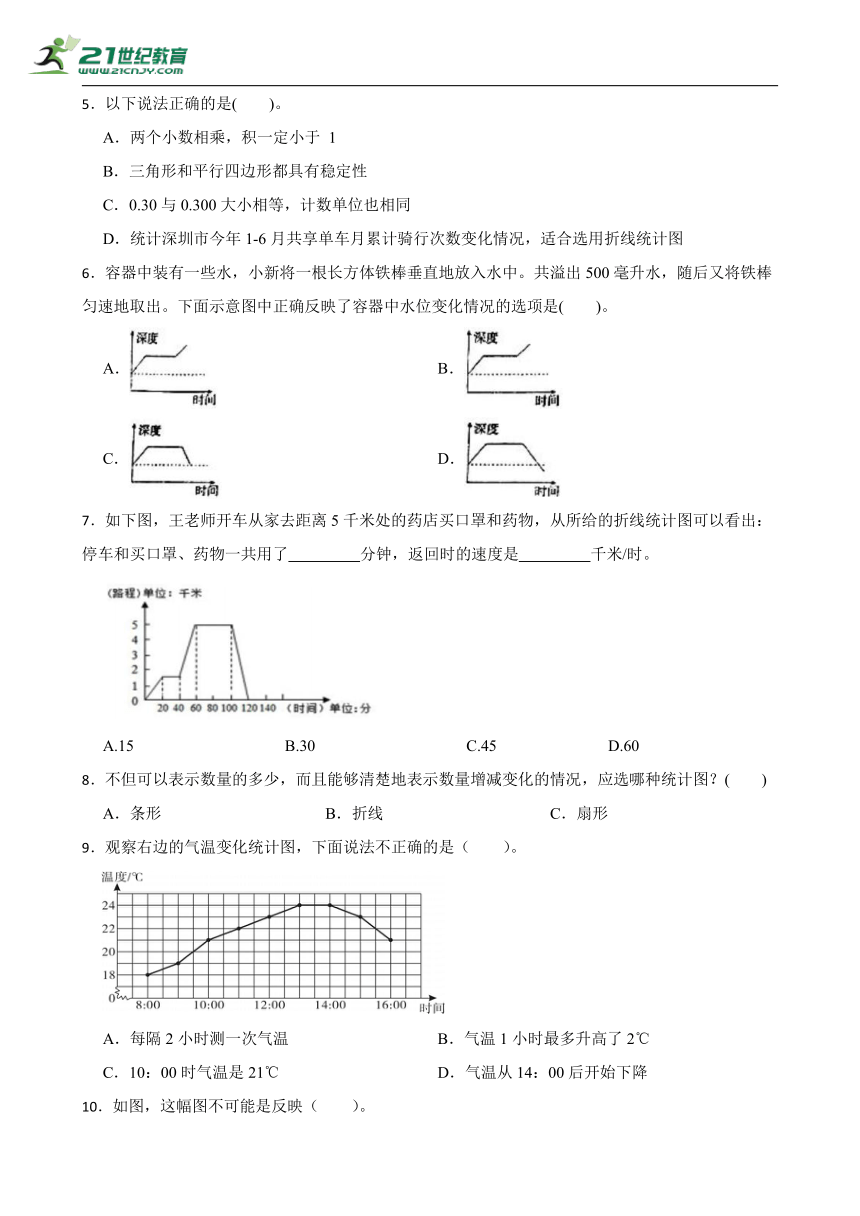
6.容器中装有一些水,小新将一根长方体铁棒垂直地放入水中。共溢出500毫升水,随后又将铁棒匀速地取出。下面示意图中正确反映了容器中水位变化情况的选项是( )。
A. B.
C. D.
7.如下图,王老师开车从家去距离5千米处的药店买口罩和药物,从所给的折线统计图可以看出:停车和买口罩、药物一共用了 分钟,返回时的速度是 千米/时。
A.15 B.30 C.45 D.60
8.不但可以表示数量的多少,而且能够清楚地表示数量增减变化的情况,应选哪种统计图?( )
A.条形 B.折线 C.扇形
9.观察右边的气温变化统计图,下面说法不正确的是( )。
A.每隔2小时测一次气温 B.气温1小时最多升高了2℃
C.10:00时气温是21℃ D.气温从14:00后开始下降
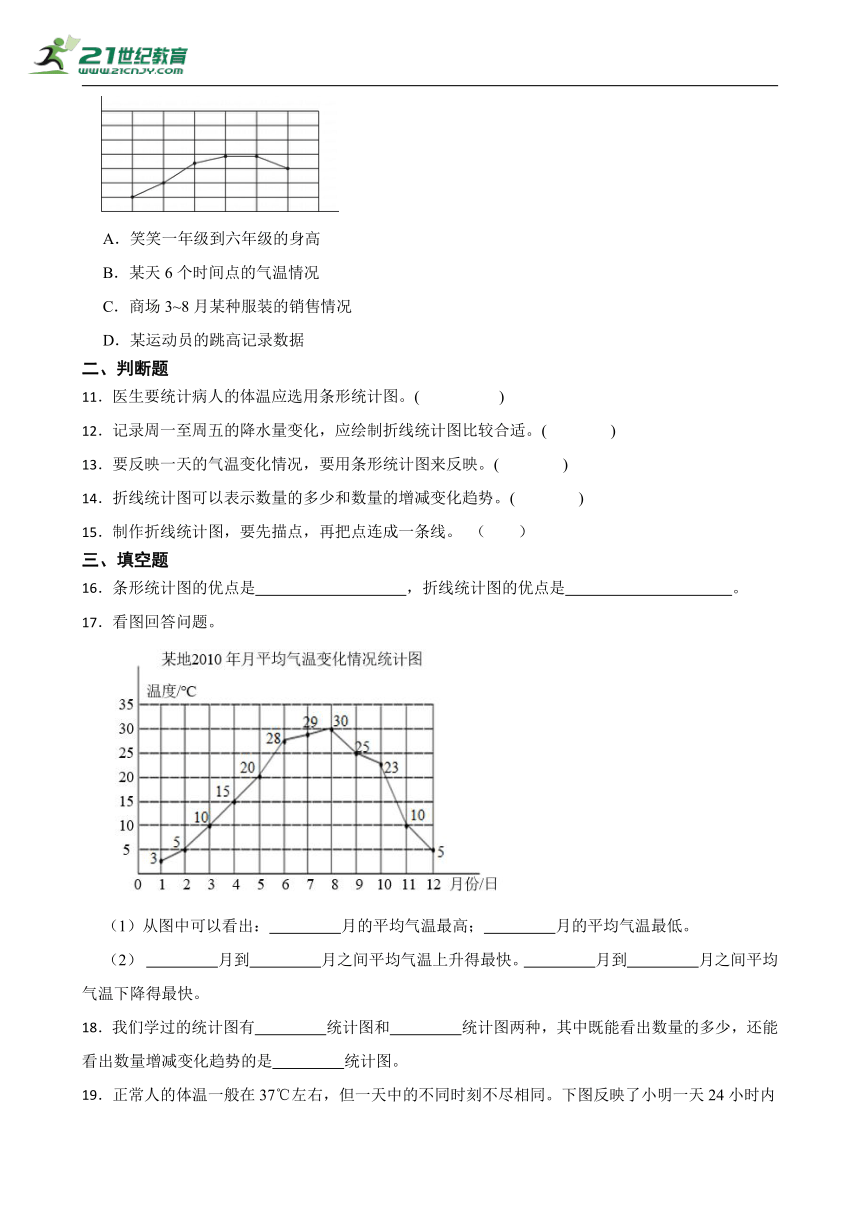
10.如图,这幅图不可能是反映( )。
A.笑笑一年级到六年级的身高
B.某天6个时间点的气温情况
C.商场3~8月某种服装的销售情况
D.某运动员的跳高记录数据
二、判断题
11.医生要统计病人的体温应选用条形统计图。( )
12.记录周一至周五的降水量变化,应绘制折线统计图比较合适。( )
13.要反映一天的气温变化情况,要用条形统计图来反映。( )
14.折线统计图可以表示数量的多少和数量的增减变化趋势。( )
15.制作折线统计图,要先描点,再把点连成一条线。 ( )
三、填空题
16.条形统计图的优点是 ,折线统计图的优点是 。
17.看图回答问题。
(1)从图中可以看出: 月的平均气温最高; 月的平均气温最低。
(2) 月到 月之间平均气温上升得最快。 月到 月之间平均气温下降得最快。
18.我们学过的统计图有 统计图和 统计图两种,其中既能看出数量的多少,还能看出数量增减变化趋势的是 统计图。
19.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同。下图反映了小明一天24小时内体温的变化情况,那么小明一天中的体温从 时到 时一直在升高。
20.我们学过 统计图和 统计图。
21.既能表示出数量的多少,又能表示出数量增减变化情况的是 统计图。
22.每年生日那天小明都会测量并记录自己的身高,下图是小明6-12岁的身高变化情况,小胖观察了统计图后认为小明8岁半时的身高正好是135厘米,你同意他的观点吗?请简述你的想法。
我 他的观点。
23.看折线统计图回答问题
(1) 时到 时人流量下降幅度最大。
(2)地铁人流高峰出现在 时和 时。
(3)13时的人流量和21时的人流量相差 人次。
24.要想反映青白江凤凰湖樱花节期间每天游园人数的变化情况,应选择 统计图。
25.下图是鹏鹏根据“一壶水加热”实验数据制作的水温变化情况图。加热前水温是 ℃,水加热到60℃时,用了是 分钟。估测一下,烧开这壶水(水温为100℃)大约需要用 分钟。
四、解决问题
26.下面是2014年至2018年某市轿车拥有量统计表。
年份 2014 2015 2016 2017 2018
辆数(万辆) 38 46 54 64 81
(1)根据表中数据把折线统计图画完整。
(2)观察统计图可知,五年来汽车拥有量呈 趋势, 年至 年增长得最快。
(3)预测2019年此市轿车数量将会达到 万辆。
理由是: 。
27. 一个高60厘米的长方体水箱中装有A、B两个进水管。先开A管,过一段时间两管同时打开。下表表示水箱的深度与时间的关系,请你回答以下问题:
时间/分 0 1 2 3 4 5 6 7
高度/厘米 0 2 4 6 9 12 15 18
(1)根据统计表,完成统计图。
(2)第 分钟以后,A、B两管同时打开,A、B两管同时刚打开时水深是 厘米。
(3)A、B两管同时进水后,每分水面升高 厘米。
28.下图是一个病人住院期间体温变化情况统计图。
(1)这种统计图是 统计图。
(2)护士每隔 小时给病人量一次体温。
(3)这位病人住院期间的体温最高是 ℃;最低是 ℃。
(4)从体温上看,这位病人的病情是在恶化还是好转?为什么?
答案解析部分
1.B
解:气象小组的同学要绘制一幅统计图公布上星期每天平均气温的变化情况,应选用折线统计图。
故答案为:B。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
2.C
解:A项:在这十天中13日治愈出院折线的点最矮,说明人数最少,原题干说法正确;
B项:这十天治愈出院人数都大于1000人,也就是都超过千人,原题干说法正确;
C项:这十天治愈出院的人数时升时降,但总体是上升的,原题干说法错误;
D项:照这个趋势22日治愈出院的人数有可能会增加,原题干说法正确。
故答案为:C。
折线统计图能清楚地看出数量的增减变化情况,折线的点高的数量就多,反之数量就少。
3.D
解:由于折线有高有低,所以不可能表示小明从1岁到6岁每年的身高。
故答案为:D。
折线统计图就是运用折线高低走势来表示数量的增减变化情况。1岁到6岁的身高会一直增加,不会忽高忽低,由此判断即可。
4.B
解:①过已知直线外一点,只能画1条原来直线的平行线,原题干说法正确;
②在0.45和0.47之间有无数个小数,原题干说法错误;
③要反映小亚生病期间的体温变化情况,选择折线统计图比较合适,原题干说法正确;
④在同一平面内,如果两条直线不平行,那么这两条直线就相交, 原题干说法错误。
故答案为:B。
①过已知直线外一点,只能画1条原来直线的平行线;
②任何两个不相等的小数之间有无数个小数;
③折线统计图能清楚的看出数量的增减变化情况,所以要反映小亚生病期间的体温变化情况,选择折线统计图比较合适;
④在同一平面内,如果两条直线不平行,那么这两条直线就相交。
5.D
解:A:2.1×5.1=10.71,两个小数相乘,积不一定小于1 ,原题说法错误,
B:三角形具有稳定性,平行四边形具有不稳定性,原题说法错误,
C:0.30与0.300大小相等,计数单位不相同 ,原题说法错误;
D:记录变化情况,适合选用折线统计图,原题说法正确。
故答案为:D。
小数的性质:小数的末尾添上或者去掉0,小数的大小不变;
一位小数的计数单位是0.1,两位小数的计数单位是0.01,三位小数的计数单位是0.001,以此类推。
6.D
解:容器内水的深度是图中的虚线,随着铁棒放入水中,水的深度逐渐增加,当溢出500毫升水后,水最深;当将铁棒匀速地取出时,水位逐渐下降,完全取出时,水位降到比原来没有放铁棒时还低的位置,第四个图正确反映了容器中水位变化情况。
故答案为:D。
第四幅图,最后水的深度比虚线还低,是因为少了500毫升水,据此可以判断D正确。
7.D;A
解:停车和买口罩、药物用了:(40-20)+(100-60)
=20+40
=60(分钟);
返回的时间:120-100=20(分)=时
返回时的速度:5÷=15(千米/时);
故答案为:D;A。
由折线图可以看出,王老师在20~40分钟和60~100分钟时停车和买口罩、药物,分别计算出这两段时间再相加即可;路程是5千米,100分~120分是返回时间,求速度,用路程除以时间。
8.B
不但可以表示数量的多少,而且能够清楚地表示数量增减变化的情况,符合折线统计图的特点。
故选:B
折线统计图的特点是不但可以表示数量的多少,而且能够清楚地表示数量增减变化的情况。
9.A
解:从图中可以看出,每隔1小时测一次气温,故A说法错误。
故答案为:A。
从图中可以看出,图中每隔1小时描1点,所以是每隔1小时测一次气温。
10.A
解:不可能反映的是笑笑一年级到六年级的身高;
故答案为:A。
笑笑从一年级到六年级,身高只会越来越高,长大一定的高度就会固定不变,不会减少,而图中的折线,是先升高,后减少,所以不对。
11.错误
解:折线统计图能清楚地看出数量的增减变化情况,医生要统计病人的体温应选用折线统计图。
故答案为:错误。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
12.正确
解:记录周一至周五的降水量变化,应绘制折线统计图比较合适,原题干说法正确。
故答案为:正确。
记录周一至周五的降水量变化,需要放映降水量的增减变化情况,应绘制折线统计图比较合适。
13.错误
解:要反映一天的气温变化情况,要用折线统计图来反映。
故答案为:错误。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
14.正确
解:折线统计图可以表示数量的多少和数量的增减变化趋势,原题干说法正确。
故答案为:正确。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
15.正确
制作折线统计图,要先描点,再把点连成一条线,此题说法正确。
故答案为:正确。
此题主要考查了折线统计图的知识,绘制折线统计图时,先描点,再把点连成一条线,据此判断。
16.体现每组中的具体数据,易比较数据之间的差距;反映数量的多少,更能反映数量的增减变化。
解:条形统计图的优点是体现每组中的具体数据,易比较数据之间的差距;
折线统计图的优点是反映数量的多少,更能反映数量的增减变化。
故答案为:体现每组中的具体数据,易比较数据之间的差距;反映数量的多少,更能反映数量的增减变化。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情
17.(1)8;1
(2)5;6;10;11
解:(1)从图中可以看出:8月的平均气温最高;1月的平均气温最低;
(2)5月到6月之间平均气温上升得最快;
10月到11月之间平均气温下降得最快。
故答案为:(1)8;1;(2)5;6;10;11。
(1)从图中可以看出:8月的平均气温最高;1月的平均气温最低;
(2)折线统计图中折线上升越陡峭说明上升的越快,反之折线下降越陡峭说明下降的越快。
18.条形;折线;折线
解:我们学过的统计图有条形统计图和折线统计图两种,其中既能看出数量的多少,还能看出数量增减变化趋势的是折线统计图。
故答案为:条形;折线;折线。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
19.5;17
解:从折线统计图中可知:小明一天中的体温从5时到17时一直在升高。
故答案为:5;17。
观察折线统计图折线的趋势可知:小明一天中的体温从5时到17时一直在升高。
20.条形;折线
解:我们学过条形统计图和折线统计图。
故答案为:条形;折线。
小学四年级已经学过条形统计图和折线统计图。
21.折线
解:既能表示出数量的多少,又能表示出数量增减变化情况的是折线统计图。
故答案为:折线。
条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
22.不同意;在实际生活中,小明的升高受多种因素影响,每年增长的量不一定相同。
解:我同意他的观点。
因为统计图中小明8岁半时对应的身高是135厘米。
故答案为:同意;统计图中小明8岁半时对应的身高是135厘米。
横轴表示岁数,竖轴表示身高,每格表示5厘米,根据横轴上8岁半时对应的点确定身高即可。
23.(1)8;9
(2)8;17
(3)5600
解:(1)8时到9时人流量下降幅度最大;
(2)地铁人流高峰出现在8时和17时;
(3)8800-3200=5600(人)。
故答案为:(1)8;9;(2)8;17;(3)5600。
(1)8时到9时的直条下降最陡峭,则说明人流量下降幅度最大;
(2)折线统计图中折线的最高点分别是8时和17时,则说明地铁人流高峰出现在8时和17时;
(3)13时的人流量和21时的人流量相差的人数=21时的人数-13时的人数。
24.折线
解:要想反映每天游园人数的变化情况,应选择折线统计图。
故答案为:折线。
折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
25.25;4;9
解:当时间是0时,水的温度是25℃,所以加热前水温是25℃,水加热到60℃时,用了是4分钟。估测一下,烧开这壶水(水温为100℃)大约需要用9分钟。
故答案为:25;4;9。
统计图横轴表示时间,纵轴表示水温,加热前水温是25℃,水加热到60℃时,用了是4分钟。每分钟大约水温上升7分钟,所以烧开这壶水(水温为100℃)大约需要用9分钟。
26.(1)解:
(2)增长;2017;2018
(3)100;从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
解:(2)观察统计图可知,五年来汽车拥有量呈增长趋势,2017年至2018年增长得最快;
(3)预测2019年此市轿车数量将会达到100万辆。
理由是:从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
故答案为:(2)增长;2017;2018;(3)100;从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
(1)依据统计表中的数据,描出各点,再连接成线,并且标上数据;
(2)2017年至2018年折线增长的最陡峭,说明增长得最快;
(3)从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
27.(1)解:
(2)3;6
(3)3
解:(2)第3分钟以后,A、B两管同时打开,A、B两管同时刚打开时水深是6厘米;
(3)12-9=3(厘米)
15-12=3(厘米)
18-15=3(厘米),A、B两管同时进水后,每分水面升高3厘米。
故答案为:(2)3;6;(3)3。
(1)依据统计表中的数据,描出各点,再连接成线,并且标上数据;
(2)第3分钟以后,水的高度明显增加,则是A、B两管同时打开,A、B两管同时刚打开,此时的水深是6厘米;
(3)A、B两管同时进水后,每分水面升高的高度=相邻两个时间段的高度差。
28.(1)折线
(2)6
(3)39.5;36.8
(4)解:这个病人的情况逐渐好转;因体温逐渐下降,接近正常体温,并且稳定下来。
解:(1)这种统计图是折线统计图;
(2)12-6=6(小时);
(3)这位病人住院期间的体温最高是39.5℃;最低是36.8℃。
故答案为:(1)折线;(2)6;(3)39.5;36.8。
(1)这种统计图是折线统计图;
(2)相邻两次测体温的时刻相减=6小时,说明护士每隔6小时给病人量一次体温;
(3)观察折线统计图,这位病人住院期间的体温最高是39.5℃;最低是36.8℃;
(4)这个病人的情况逐渐好转;因体温逐渐下降,接近正常体温,并且稳定下来。
一、单选题
1.气象小组的同学要绘制一幅统计图公布上星期每天平均气温的变化情况,应选用( )统计图.
A.条形 B.折线 C.扇形
2.笑笑把2月12日到2月21日全国新冠肺炎患者治愈出院的人数制成了下面的折线统计图。
根据图中信息可以判断,下列描述错误的是( )。
A.在这十天中13日治愈出院的人数最少
B.这十天治愈出院人数都超过千人
C.这十天治愈出院的人数一直在不断上升
D.照这个趋势22日治愈出院的人数有可能会增加
3.下面的折线统计图,不可能表示的是( )
A.小胖连续6次的数学考试成绩 B.某地连续6天每日最高气温情况
C.超市上半年每月的营业总额 D.小明从1岁到6岁每年的身高
4.下列的表述中有( )句是正确的。
①在同一个平面内,过已知直线a外一点P,只能画1条与直线a平行的直线;
②在0.45和0.47之间只有一个小数是46,
③要反映小亚生病期间的体温变化情况,选择折线统计图比较合适;
④如果两条直线不平行,那么这两条直线一定互相垂直。
A.1 B.2 C.3 D.4
5.以下说法正确的是( )。
A.两个小数相乘,积一定小于 1
B.三角形和平行四边形都具有稳定性
C.0.30与0.300大小相等,计数单位也相同
D.统计深圳市今年1-6月共享单车月累计骑行次数变化情况,适合选用折线统计图
6.容器中装有一些水,小新将一根长方体铁棒垂直地放入水中。共溢出500毫升水,随后又将铁棒匀速地取出。下面示意图中正确反映了容器中水位变化情况的选项是( )。
A. B.
C. D.
7.如下图,王老师开车从家去距离5千米处的药店买口罩和药物,从所给的折线统计图可以看出:停车和买口罩、药物一共用了 分钟,返回时的速度是 千米/时。
A.15 B.30 C.45 D.60
8.不但可以表示数量的多少,而且能够清楚地表示数量增减变化的情况,应选哪种统计图?( )
A.条形 B.折线 C.扇形
9.观察右边的气温变化统计图,下面说法不正确的是( )。
A.每隔2小时测一次气温 B.气温1小时最多升高了2℃
C.10:00时气温是21℃ D.气温从14:00后开始下降
10.如图,这幅图不可能是反映( )。
A.笑笑一年级到六年级的身高
B.某天6个时间点的气温情况
C.商场3~8月某种服装的销售情况
D.某运动员的跳高记录数据
二、判断题
11.医生要统计病人的体温应选用条形统计图。( )
12.记录周一至周五的降水量变化,应绘制折线统计图比较合适。( )
13.要反映一天的气温变化情况,要用条形统计图来反映。( )
14.折线统计图可以表示数量的多少和数量的增减变化趋势。( )
15.制作折线统计图,要先描点,再把点连成一条线。 ( )
三、填空题
16.条形统计图的优点是 ,折线统计图的优点是 。
17.看图回答问题。
(1)从图中可以看出: 月的平均气温最高; 月的平均气温最低。
(2) 月到 月之间平均气温上升得最快。 月到 月之间平均气温下降得最快。
18.我们学过的统计图有 统计图和 统计图两种,其中既能看出数量的多少,还能看出数量增减变化趋势的是 统计图。
19.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同。下图反映了小明一天24小时内体温的变化情况,那么小明一天中的体温从 时到 时一直在升高。
20.我们学过 统计图和 统计图。
21.既能表示出数量的多少,又能表示出数量增减变化情况的是 统计图。
22.每年生日那天小明都会测量并记录自己的身高,下图是小明6-12岁的身高变化情况,小胖观察了统计图后认为小明8岁半时的身高正好是135厘米,你同意他的观点吗?请简述你的想法。
我 他的观点。
23.看折线统计图回答问题
(1) 时到 时人流量下降幅度最大。
(2)地铁人流高峰出现在 时和 时。
(3)13时的人流量和21时的人流量相差 人次。
24.要想反映青白江凤凰湖樱花节期间每天游园人数的变化情况,应选择 统计图。
25.下图是鹏鹏根据“一壶水加热”实验数据制作的水温变化情况图。加热前水温是 ℃,水加热到60℃时,用了是 分钟。估测一下,烧开这壶水(水温为100℃)大约需要用 分钟。
四、解决问题
26.下面是2014年至2018年某市轿车拥有量统计表。
年份 2014 2015 2016 2017 2018
辆数(万辆) 38 46 54 64 81
(1)根据表中数据把折线统计图画完整。
(2)观察统计图可知,五年来汽车拥有量呈 趋势, 年至 年增长得最快。
(3)预测2019年此市轿车数量将会达到 万辆。
理由是: 。
27. 一个高60厘米的长方体水箱中装有A、B两个进水管。先开A管,过一段时间两管同时打开。下表表示水箱的深度与时间的关系,请你回答以下问题:
时间/分 0 1 2 3 4 5 6 7
高度/厘米 0 2 4 6 9 12 15 18
(1)根据统计表,完成统计图。
(2)第 分钟以后,A、B两管同时打开,A、B两管同时刚打开时水深是 厘米。
(3)A、B两管同时进水后,每分水面升高 厘米。
28.下图是一个病人住院期间体温变化情况统计图。
(1)这种统计图是 统计图。
(2)护士每隔 小时给病人量一次体温。
(3)这位病人住院期间的体温最高是 ℃;最低是 ℃。
(4)从体温上看,这位病人的病情是在恶化还是好转?为什么?
答案解析部分
1.B
解:气象小组的同学要绘制一幅统计图公布上星期每天平均气温的变化情况,应选用折线统计图。
故答案为:B。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
2.C
解:A项:在这十天中13日治愈出院折线的点最矮,说明人数最少,原题干说法正确;
B项:这十天治愈出院人数都大于1000人,也就是都超过千人,原题干说法正确;
C项:这十天治愈出院的人数时升时降,但总体是上升的,原题干说法错误;
D项:照这个趋势22日治愈出院的人数有可能会增加,原题干说法正确。
故答案为:C。
折线统计图能清楚地看出数量的增减变化情况,折线的点高的数量就多,反之数量就少。
3.D
解:由于折线有高有低,所以不可能表示小明从1岁到6岁每年的身高。
故答案为:D。
折线统计图就是运用折线高低走势来表示数量的增减变化情况。1岁到6岁的身高会一直增加,不会忽高忽低,由此判断即可。
4.B
解:①过已知直线外一点,只能画1条原来直线的平行线,原题干说法正确;
②在0.45和0.47之间有无数个小数,原题干说法错误;
③要反映小亚生病期间的体温变化情况,选择折线统计图比较合适,原题干说法正确;
④在同一平面内,如果两条直线不平行,那么这两条直线就相交, 原题干说法错误。
故答案为:B。
①过已知直线外一点,只能画1条原来直线的平行线;
②任何两个不相等的小数之间有无数个小数;
③折线统计图能清楚的看出数量的增减变化情况,所以要反映小亚生病期间的体温变化情况,选择折线统计图比较合适;
④在同一平面内,如果两条直线不平行,那么这两条直线就相交。
5.D
解:A:2.1×5.1=10.71,两个小数相乘,积不一定小于1 ,原题说法错误,
B:三角形具有稳定性,平行四边形具有不稳定性,原题说法错误,
C:0.30与0.300大小相等,计数单位不相同 ,原题说法错误;
D:记录变化情况,适合选用折线统计图,原题说法正确。
故答案为:D。
小数的性质:小数的末尾添上或者去掉0,小数的大小不变;
一位小数的计数单位是0.1,两位小数的计数单位是0.01,三位小数的计数单位是0.001,以此类推。
6.D
解:容器内水的深度是图中的虚线,随着铁棒放入水中,水的深度逐渐增加,当溢出500毫升水后,水最深;当将铁棒匀速地取出时,水位逐渐下降,完全取出时,水位降到比原来没有放铁棒时还低的位置,第四个图正确反映了容器中水位变化情况。
故答案为:D。
第四幅图,最后水的深度比虚线还低,是因为少了500毫升水,据此可以判断D正确。
7.D;A
解:停车和买口罩、药物用了:(40-20)+(100-60)
=20+40
=60(分钟);
返回的时间:120-100=20(分)=时
返回时的速度:5÷=15(千米/时);
故答案为:D;A。
由折线图可以看出,王老师在20~40分钟和60~100分钟时停车和买口罩、药物,分别计算出这两段时间再相加即可;路程是5千米,100分~120分是返回时间,求速度,用路程除以时间。
8.B
不但可以表示数量的多少,而且能够清楚地表示数量增减变化的情况,符合折线统计图的特点。
故选:B
折线统计图的特点是不但可以表示数量的多少,而且能够清楚地表示数量增减变化的情况。
9.A
解:从图中可以看出,每隔1小时测一次气温,故A说法错误。
故答案为:A。
从图中可以看出,图中每隔1小时描1点,所以是每隔1小时测一次气温。
10.A
解:不可能反映的是笑笑一年级到六年级的身高;
故答案为:A。
笑笑从一年级到六年级,身高只会越来越高,长大一定的高度就会固定不变,不会减少,而图中的折线,是先升高,后减少,所以不对。
11.错误
解:折线统计图能清楚地看出数量的增减变化情况,医生要统计病人的体温应选用折线统计图。
故答案为:错误。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
12.正确
解:记录周一至周五的降水量变化,应绘制折线统计图比较合适,原题干说法正确。
故答案为:正确。
记录周一至周五的降水量变化,需要放映降水量的增减变化情况,应绘制折线统计图比较合适。
13.错误
解:要反映一天的气温变化情况,要用折线统计图来反映。
故答案为:错误。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
14.正确
解:折线统计图可以表示数量的多少和数量的增减变化趋势,原题干说法正确。
故答案为:正确。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
15.正确
制作折线统计图,要先描点,再把点连成一条线,此题说法正确。
故答案为:正确。
此题主要考查了折线统计图的知识,绘制折线统计图时,先描点,再把点连成一条线,据此判断。
16.体现每组中的具体数据,易比较数据之间的差距;反映数量的多少,更能反映数量的增减变化。
解:条形统计图的优点是体现每组中的具体数据,易比较数据之间的差距;
折线统计图的优点是反映数量的多少,更能反映数量的增减变化。
故答案为:体现每组中的具体数据,易比较数据之间的差距;反映数量的多少,更能反映数量的增减变化。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情
17.(1)8;1
(2)5;6;10;11
解:(1)从图中可以看出:8月的平均气温最高;1月的平均气温最低;
(2)5月到6月之间平均气温上升得最快;
10月到11月之间平均气温下降得最快。
故答案为:(1)8;1;(2)5;6;10;11。
(1)从图中可以看出:8月的平均气温最高;1月的平均气温最低;
(2)折线统计图中折线上升越陡峭说明上升的越快,反之折线下降越陡峭说明下降的越快。
18.条形;折线;折线
解:我们学过的统计图有条形统计图和折线统计图两种,其中既能看出数量的多少,还能看出数量增减变化趋势的是折线统计图。
故答案为:条形;折线;折线。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
19.5;17
解:从折线统计图中可知:小明一天中的体温从5时到17时一直在升高。
故答案为:5;17。
观察折线统计图折线的趋势可知:小明一天中的体温从5时到17时一直在升高。
20.条形;折线
解:我们学过条形统计图和折线统计图。
故答案为:条形;折线。
小学四年级已经学过条形统计图和折线统计图。
21.折线
解:既能表示出数量的多少,又能表示出数量增减变化情况的是折线统计图。
故答案为:折线。
条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
22.不同意;在实际生活中,小明的升高受多种因素影响,每年增长的量不一定相同。
解:我同意他的观点。
因为统计图中小明8岁半时对应的身高是135厘米。
故答案为:同意;统计图中小明8岁半时对应的身高是135厘米。
横轴表示岁数,竖轴表示身高,每格表示5厘米,根据横轴上8岁半时对应的点确定身高即可。
23.(1)8;9
(2)8;17
(3)5600
解:(1)8时到9时人流量下降幅度最大;
(2)地铁人流高峰出现在8时和17时;
(3)8800-3200=5600(人)。
故答案为:(1)8;9;(2)8;17;(3)5600。
(1)8时到9时的直条下降最陡峭,则说明人流量下降幅度最大;
(2)折线统计图中折线的最高点分别是8时和17时,则说明地铁人流高峰出现在8时和17时;
(3)13时的人流量和21时的人流量相差的人数=21时的人数-13时的人数。
24.折线
解:要想反映每天游园人数的变化情况,应选择折线统计图。
故答案为:折线。
折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
25.25;4;9
解:当时间是0时,水的温度是25℃,所以加热前水温是25℃,水加热到60℃时,用了是4分钟。估测一下,烧开这壶水(水温为100℃)大约需要用9分钟。
故答案为:25;4;9。
统计图横轴表示时间,纵轴表示水温,加热前水温是25℃,水加热到60℃时,用了是4分钟。每分钟大约水温上升7分钟,所以烧开这壶水(水温为100℃)大约需要用9分钟。
26.(1)解:
(2)增长;2017;2018
(3)100;从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
解:(2)观察统计图可知,五年来汽车拥有量呈增长趋势,2017年至2018年增长得最快;
(3)预测2019年此市轿车数量将会达到100万辆。
理由是:从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
故答案为:(2)增长;2017;2018;(3)100;从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
(1)依据统计表中的数据,描出各点,再连接成线,并且标上数据;
(2)2017年至2018年折线增长的最陡峭,说明增长得最快;
(3)从2014年到2018年,该市轿车数量逐年增长且增长幅度越来越大,所以预测2019年轿车数量将会达到100万辆。
27.(1)解:
(2)3;6
(3)3
解:(2)第3分钟以后,A、B两管同时打开,A、B两管同时刚打开时水深是6厘米;
(3)12-9=3(厘米)
15-12=3(厘米)
18-15=3(厘米),A、B两管同时进水后,每分水面升高3厘米。
故答案为:(2)3;6;(3)3。
(1)依据统计表中的数据,描出各点,再连接成线,并且标上数据;
(2)第3分钟以后,水的高度明显增加,则是A、B两管同时打开,A、B两管同时刚打开,此时的水深是6厘米;
(3)A、B两管同时进水后,每分水面升高的高度=相邻两个时间段的高度差。
28.(1)折线
(2)6
(3)39.5;36.8
(4)解:这个病人的情况逐渐好转;因体温逐渐下降,接近正常体温,并且稳定下来。
解:(1)这种统计图是折线统计图;
(2)12-6=6(小时);
(3)这位病人住院期间的体温最高是39.5℃;最低是36.8℃。
故答案为:(1)折线;(2)6;(3)39.5;36.8。
(1)这种统计图是折线统计图;
(2)相邻两次测体温的时刻相减=6小时,说明护士每隔6小时给病人量一次体温;
(3)观察折线统计图,这位病人住院期间的体温最高是39.5℃;最低是36.8℃;
(4)这个病人的情况逐渐好转;因体温逐渐下降,接近正常体温,并且稳定下来。
