5.2菱形培优练习 浙教版2024—2025学年八年级下册(含答案)
文档属性
| 名称 | 5.2菱形培优练习 浙教版2024—2025学年八年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 649.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-08 22:04:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.2菱形培优练习浙教版2024—2025学年八年级下册
一、选择题
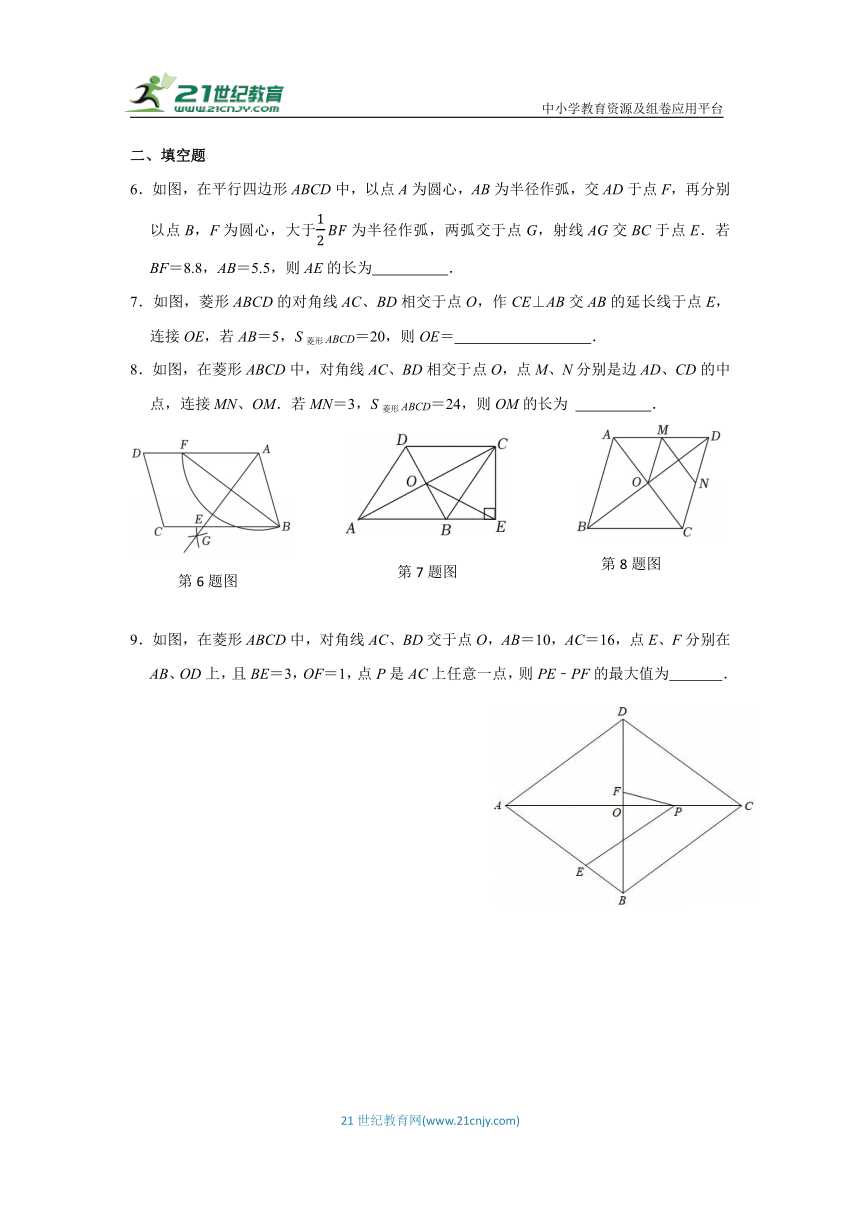
1.已知如图,菱形ABCD中,对角线AC与BD相交于点O,DE⊥AB于E,交AC于点F,若∠BAD=α,则∠DFO一定等于( )
A.2α B.45°+α C. D.
2.如图,AC为菱形ABCD的对角线,∠ACD=30°,过点D作DE⊥BC,垂足为点E,则( )
A. B. C. D.
3.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
4.如图,在菱形ABCD中,AC、BD交于O点,AC=24,BD=10,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
5.如图1,动点P从菱形ABCD的点A出发,沿边AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点P运动到BC中点时,PO的长为( )
A.2 B.3 C. D.
二、填空题
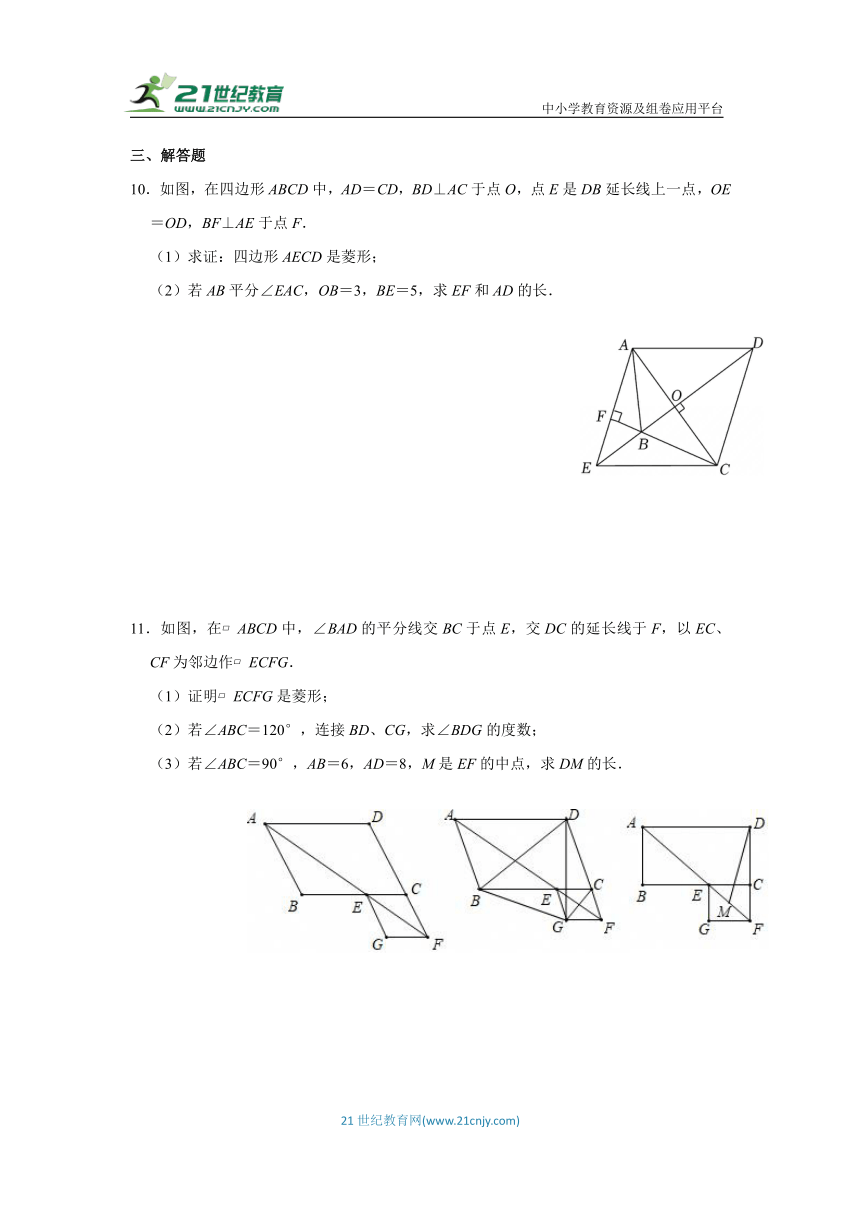
6.如图,在平行四边形ABCD中,以点A为圆心,AB为半径作弧,交AD于点F,再分别以点B,F为圆心,大于为半径作弧,两弧交于点G,射线AG交BC于点E.若BF=8.8,AB=5.5,则AE的长为 .
7.如图,菱形ABCD的对角线AC、BD相交于点O,作CE⊥AB交AB的延长线于点E,连接OE,若AB=5,S菱形ABCD=20,则OE= .
8.如图,在菱形ABCD中,对角线AC、BD相交于点O,点M、N分别是边AD、CD的中点,连接MN、OM.若MN=3,S菱形ABCD=24,则OM的长为 .
9.如图,在菱形ABCD中,对角线AC、BD交于点O,AB=10,AC=16,点E、F分别在AB、OD上,且BE=3,OF=1,点P是AC上任意一点,则PE﹣PF的最大值为 .
三、解答题
10.如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.
(1)求证:四边形AECD是菱形;
(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.
11.如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
12.已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的面积.
13.如图,在 ABCD中,M、N分别是AD、BC的中点,∠AND=90°,连接CM交DN于点O.
(1)求证:△ABN≌△CDM;
(2)求证:四边形CDMN为菱形;
(3)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求NC的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:∠DAC=∠DCA;
(2)求证:四边形ABCD是菱形;
(3)若AB,BD=2,求OE的长.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C B A D C
1.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,∠BAO∠BAD,
∴∠DFO+∠FDO=90°,
∵DE⊥AB,
∴∠FDO+∠ABO=90°,
∴∠DFO=∠ABO,
∵∠BAO+∠ABO=90°,
∴∠DFO=90°﹣∠BAO=90°,
故选:C.
2.【解答】解:由题意可知,四边形ABCD是菱形,
∴CD=AD=CB,且AC平分∠BCD,
∵∠ACD=30°,
∴∠BCD=2∠ACD=2×30°=60°,
∵DE⊥BC,
∴∠DEC=90°,
在Rt△CDE中,∠CDE=30°,
∴,
即,
故选:B.
3.【解答】解:∵四边形ABCD是菱形,AC=6,BD=8,
∴AC⊥BD,OC=OAAC=3,OB=ODBD=4,
∴∠BOC=90°,
∴BC5,
∵AE⊥BC于点E,
∴S菱形ABCD=5AE6×8,
∴AE,
故选:A.
4.【解答】解:如图,连接PD,
∵四边形ABCD是菱形,
∴AC与BD互相垂直平分,
∴AO=OC=12,BO=DO=5,
∴AD=CD13,
∵S△ACD=S△APD+S△CPD,PM⊥AD,PN⊥CD,
∴,
∴24×5=13(PM+PN),
∴PM+PN,
故选:D.
5.【解答】解:结合图象,得到当x=0时,PO=AO=4,
∴当点P运动到点B时,PO=BO=2,
∵菱形ABCD,
∴AC⊥BD,
∴∠AOB=∠BOC=90°,
∴,
当点P运动到BC中点时,PO的长为,
故选:C.
二、填空题
6.【解答】如图,连接EF,设AE交BF于点O,
由作图可知:AE⊥BF,OB=OF=4.4,∠BAE=∠EAF,
由条件可知AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF=5.5,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,
在Rt△AOB中,∵∠AOB=90°,AB=5.5,
∴,
∴AE=2OA=6.6.
故答案为:6.6.
7.【解答】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,OA=OC,BD⊥AC,
∵CE⊥AB,菱形ABCD的面积为20,
∴S菱形ABCD=AB CE=5CE=20,
∴CE=4,
在Rt△BCE中,BE3,
∴AE=AB+BE=8,
在Rt△ACE中,AC4,
∵OA=OC,
∴OEAC=2,
故答案为:2.
8.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,,,
∴∠AOD=90°,
∵MN=3,点M、N分别是边AD、CD的中点,
∴AC=2MN=6,
∴AO=CO=3,
∵,
∴BD=8,
∴DO=BO=4,
∴,
∴,
故答案为:2.5.
9.【解答】答案为:4.
三、解答题
10.【解答】(1)证明:∵AD=CD,BD⊥AC,
∴OA=OC,
∵OE=OD,
∴四边形AECD是平行四边形,
∵AC⊥BD,
∴平行四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴OE⊥OA,
∵CF⊥AE,AB平分∠EAC,
∴BF=OB,
∴Rt△AFB≌Rt△AOB(HL),
∴AF=OA=OC,
∵BF=OB=3,BE=5,
∴EF,
∴OE=OB+BE=3+5=8,
∵∠EFB=∠AOE=90°,∠FEB=∠AEO,
即,
∴AE=10,
∵AB平分∠EAC时,F应为AE的中点,且∠AEO=30°,AO与AE的比值应为1:2,
∴AD=AE=10.
11.【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
方法二:∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC=6,
过M作MH⊥CF于H,
则△MHF是等腰直角三角形,
∵△ADF是等腰直角三角形,
∴DF=AD=8,
∵CF=CE=2,
∴MH=FH=1,
∴DM5.
12.【解答】(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
∴S菱形BMDN=DM AB=5×4=20.
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,,
∴△ABN≌△CDM(SAS);
(2)证明:∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC∥DM,NC=DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形.
(3)解:∵M是AD的中点,∠AND=90°,
∴MN=MDAD,
∴∠1=∠MND,
∵AD∥BC,
∴∠1=∠CND,
∵∠1=∠2,
∴∠MND=∠CND=∠2,
∴PN=PC,
∵CE⊥MN,
∴∠CEN=90°,
∠END+∠CNP+∠2=180°﹣∠CEN=90°,
又∵∠END=∠CNP=∠2,
∴∠2=∠PNE=30°,
∵PE=1,
∴PN=2PE=2,
∴CE=PC+PE=3,
∴NC2.
14.【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠BAD,
∴∠OAB=∠DAC,
∴∠DAC=∠DCA;
(2)证明:∵∠DAC=∠DCA,AB=AD,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(3)解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OBBD=1,
在Rt△AOB中,由勾股定理得:OA2,
∴OE=OA=2.
21世纪教育网(www.21cnjy.com)
5.2菱形培优练习浙教版2024—2025学年八年级下册
一、选择题
1.已知如图,菱形ABCD中,对角线AC与BD相交于点O,DE⊥AB于E,交AC于点F,若∠BAD=α,则∠DFO一定等于( )
A.2α B.45°+α C. D.
2.如图,AC为菱形ABCD的对角线,∠ACD=30°,过点D作DE⊥BC,垂足为点E,则( )
A. B. C. D.
3.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
4.如图,在菱形ABCD中,AC、BD交于O点,AC=24,BD=10,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
5.如图1,动点P从菱形ABCD的点A出发,沿边AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点P运动到BC中点时,PO的长为( )
A.2 B.3 C. D.
二、填空题
6.如图,在平行四边形ABCD中,以点A为圆心,AB为半径作弧,交AD于点F,再分别以点B,F为圆心,大于为半径作弧,两弧交于点G,射线AG交BC于点E.若BF=8.8,AB=5.5,则AE的长为 .
7.如图,菱形ABCD的对角线AC、BD相交于点O,作CE⊥AB交AB的延长线于点E,连接OE,若AB=5,S菱形ABCD=20,则OE= .
8.如图,在菱形ABCD中,对角线AC、BD相交于点O,点M、N分别是边AD、CD的中点,连接MN、OM.若MN=3,S菱形ABCD=24,则OM的长为 .
9.如图,在菱形ABCD中,对角线AC、BD交于点O,AB=10,AC=16,点E、F分别在AB、OD上,且BE=3,OF=1,点P是AC上任意一点,则PE﹣PF的最大值为 .
三、解答题
10.如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.
(1)求证:四边形AECD是菱形;
(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.
11.如图,在 ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作 ECFG.
(1)证明 ECFG是菱形;
(2)若∠ABC=120°,连接BD、CG,求∠BDG的度数;
(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
12.已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的面积.
13.如图,在 ABCD中,M、N分别是AD、BC的中点,∠AND=90°,连接CM交DN于点O.
(1)求证:△ABN≌△CDM;
(2)求证:四边形CDMN为菱形;
(3)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求NC的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:∠DAC=∠DCA;
(2)求证:四边形ABCD是菱形;
(3)若AB,BD=2,求OE的长.
参考答案
一、选择题
题号 1 2 3 4 5
答案 C B A D C
1.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,∠BAO∠BAD,
∴∠DFO+∠FDO=90°,
∵DE⊥AB,
∴∠FDO+∠ABO=90°,
∴∠DFO=∠ABO,
∵∠BAO+∠ABO=90°,
∴∠DFO=90°﹣∠BAO=90°,
故选:C.
2.【解答】解:由题意可知,四边形ABCD是菱形,
∴CD=AD=CB,且AC平分∠BCD,
∵∠ACD=30°,
∴∠BCD=2∠ACD=2×30°=60°,
∵DE⊥BC,
∴∠DEC=90°,
在Rt△CDE中,∠CDE=30°,
∴,
即,
故选:B.
3.【解答】解:∵四边形ABCD是菱形,AC=6,BD=8,
∴AC⊥BD,OC=OAAC=3,OB=ODBD=4,
∴∠BOC=90°,
∴BC5,
∵AE⊥BC于点E,
∴S菱形ABCD=5AE6×8,
∴AE,
故选:A.
4.【解答】解:如图,连接PD,
∵四边形ABCD是菱形,
∴AC与BD互相垂直平分,
∴AO=OC=12,BO=DO=5,
∴AD=CD13,
∵S△ACD=S△APD+S△CPD,PM⊥AD,PN⊥CD,
∴,
∴24×5=13(PM+PN),
∴PM+PN,
故选:D.
5.【解答】解:结合图象,得到当x=0时,PO=AO=4,
∴当点P运动到点B时,PO=BO=2,
∵菱形ABCD,
∴AC⊥BD,
∴∠AOB=∠BOC=90°,
∴,
当点P运动到BC中点时,PO的长为,
故选:C.
二、填空题
6.【解答】如图,连接EF,设AE交BF于点O,
由作图可知:AE⊥BF,OB=OF=4.4,∠BAE=∠EAF,
由条件可知AD∥BC,
∴∠EAF=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=AF=5.5,
∵AF∥BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴OA=OE,
在Rt△AOB中,∵∠AOB=90°,AB=5.5,
∴,
∴AE=2OA=6.6.
故答案为:6.6.
7.【解答】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,OA=OC,BD⊥AC,
∵CE⊥AB,菱形ABCD的面积为20,
∴S菱形ABCD=AB CE=5CE=20,
∴CE=4,
在Rt△BCE中,BE3,
∴AE=AB+BE=8,
在Rt△ACE中,AC4,
∵OA=OC,
∴OEAC=2,
故答案为:2.
8.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,,,
∴∠AOD=90°,
∵MN=3,点M、N分别是边AD、CD的中点,
∴AC=2MN=6,
∴AO=CO=3,
∵,
∴BD=8,
∴DO=BO=4,
∴,
∴,
故答案为:2.5.
9.【解答】答案为:4.
三、解答题
10.【解答】(1)证明:∵AD=CD,BD⊥AC,
∴OA=OC,
∵OE=OD,
∴四边形AECD是平行四边形,
∵AC⊥BD,
∴平行四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴OE⊥OA,
∵CF⊥AE,AB平分∠EAC,
∴BF=OB,
∴Rt△AFB≌Rt△AOB(HL),
∴AF=OA=OC,
∵BF=OB=3,BE=5,
∴EF,
∴OE=OB+BE=3+5=8,
∵∠EFB=∠AOE=90°,∠FEB=∠AEO,
即,
∴AE=10,
∵AB平分∠EAC时,F应为AE的中点,且∠AEO=30°,AO与AE的比值应为1:2,
∴AD=AE=10.
11.【解答】解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图2中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=6,AD=8,
∴BD=10,
∴DMBD=5.
方法二:∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC=6,
过M作MH⊥CF于H,
则△MHF是等腰直角三角形,
∵△ADF是等腰直角三角形,
∴DF=AD=8,
∵CF=CE=2,
∴MH=FH=1,
∴DM5.
12.【解答】(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
∴S菱形BMDN=DM AB=5×4=20.
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,,
∴△ABN≌△CDM(SAS);
(2)证明:∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC∥DM,NC=DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形.
(3)解:∵M是AD的中点,∠AND=90°,
∴MN=MDAD,
∴∠1=∠MND,
∵AD∥BC,
∴∠1=∠CND,
∵∠1=∠2,
∴∠MND=∠CND=∠2,
∴PN=PC,
∵CE⊥MN,
∴∠CEN=90°,
∠END+∠CNP+∠2=180°﹣∠CEN=90°,
又∵∠END=∠CNP=∠2,
∴∠2=∠PNE=30°,
∵PE=1,
∴PN=2PE=2,
∴CE=PC+PE=3,
∴NC2.
14.【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠BAD,
∴∠OAB=∠DAC,
∴∠DAC=∠DCA;
(2)证明:∵∠DAC=∠DCA,AB=AD,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴ ABCD是菱形;
(3)解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OBBD=1,
在Rt△AOB中,由勾股定理得:OA2,
∴OE=OA=2.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
