4.2平行四边形及其性质培优练习(含答案)
文档属性
| 名称 | 4.2平行四边形及其性质培优练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 709.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 22:00:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
4.2平行四边形及其性质培优练习浙教版2024—2025学年八年级下册
一、选择题
1.如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,,下列结论中,不正确的是( )
A.∠CAD=30° B.BD
C.OE D.
2.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.1cm<OA<4cm B.2cm<OA<8cm
C.2cm<OA<5cm D.3cm<OA<8cm
3.如图,在平行四边形ABCD中P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是( )
A.18 B.24 C.23 D.14
4.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E、P.连接OE,∠ADC=60°,ABBC=1,则下列结论:
①∠CAD=30°;②BD=2;③S平行四边形ABCD=AB AC;④AD=4OE.
其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,分别以△ABC的三边为一边作 BCED, ABFG, ACIH,且点D,E分别在FG,HI上.若 ABFG, ACIH的面积分别为S1,S2,则 BCED的面积为( )
A.S1+S2 B. C. D.
二、填空题
6.如图,平移图形M,与图形N可以拼成一个平行四边形,则图中∠α= °.
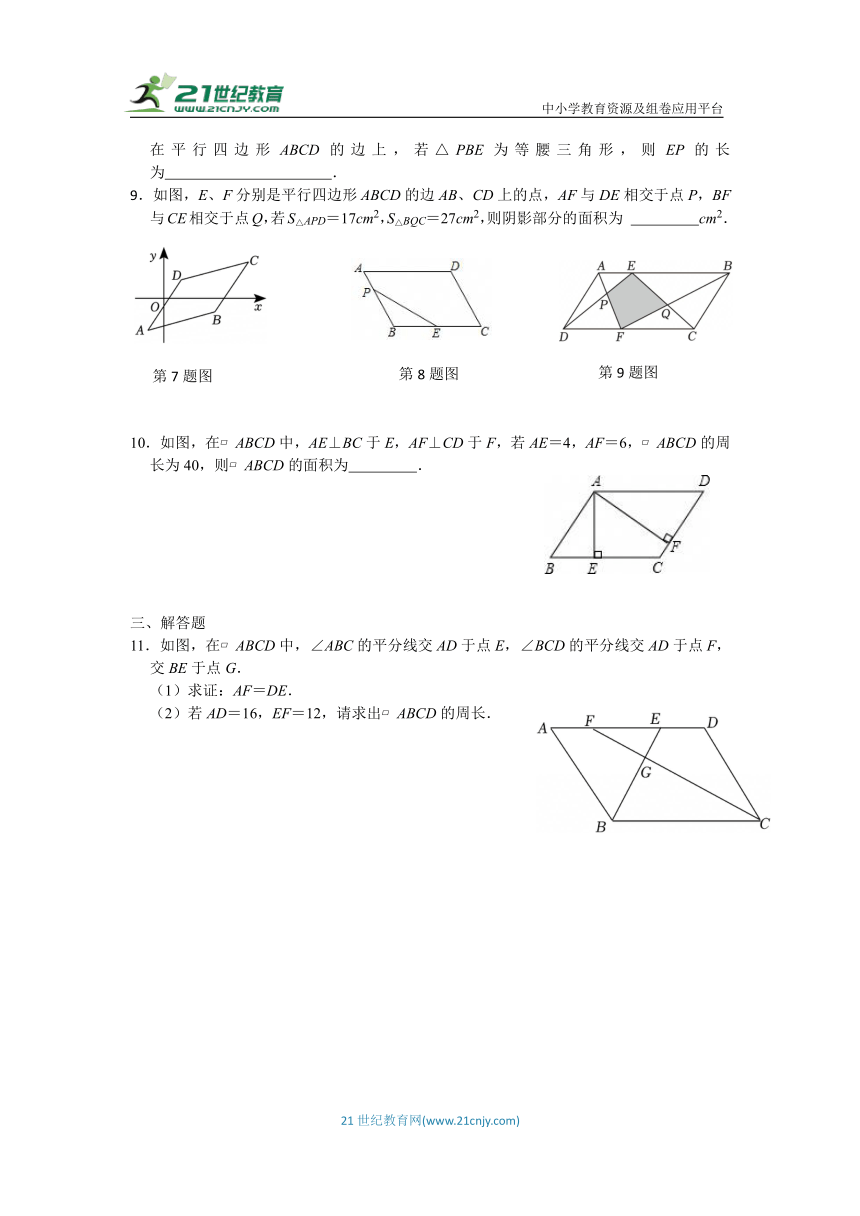
7.如图,在平面直角坐标系中,平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),则顶点B的坐标为 .
8.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为 .
9.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=17cm2,S△BQC=27cm2,则阴影部分的面积为 cm2.
10.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6, ABCD的周长为40,则 ABCD的面积为 .
三、解答题
11.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G.
(1)求证:AF=DE.
(2)若AD=16,EF=12,请求出 ABCD的周长.
12.如图,平行四边形ABCD中,AB=4cm,AD=2cm,∠C=30°.点P以2cm/s的速度从顶点A出发沿折线A﹣B﹣C向点C运动,同时点Q以1cm/s的速度从顶点A出发沿折线A﹣D﹣C向点C运动,当其中一个动点到达末端停止运动时,另一点也停止运动.设运动时间为ts.
(1)求平行四边形ABCD的面积;
(2)求当t=0.5s时,△APQ的面积;
(3)当△APQ的面积是平行四边形ABCD面积的时,求t的值.
13.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=20,CF=12,求DF的长.
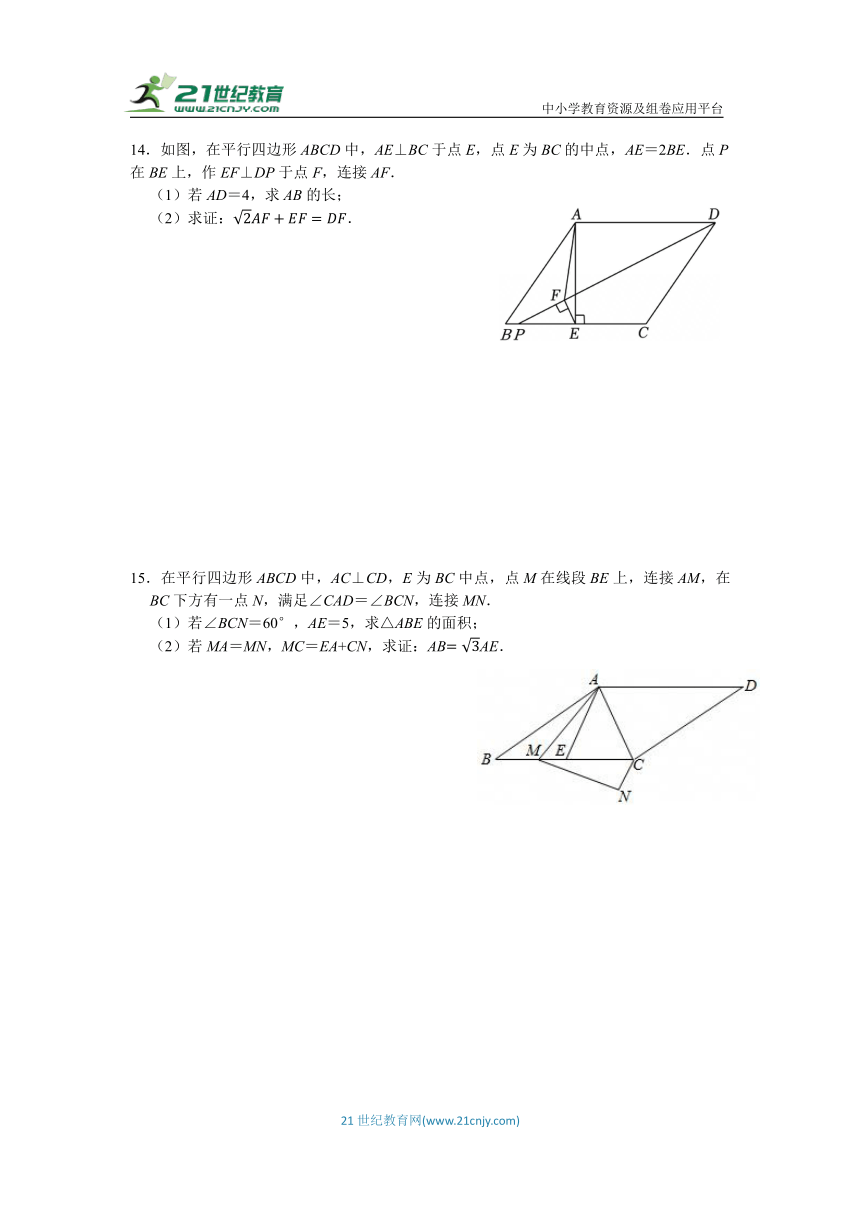
14.如图,在平行四边形ABCD中,AE⊥BC于点E,点E为BC的中点,AE=2BE.点P在BE上,作EF⊥DP于点F,连接AF.
(1)若AD=4,求AB的长;
(2)求证:.
15.在平行四边形ABCD中,AC⊥CD,E为BC中点,点M在线段BE上,连接AM,在BC下方有一点N,满足∠CAD=∠BCN,连接MN.
(1)若∠BCN=60°,AE=5,求△ABE的面积;
(2)若MA=MN,MC=EA+CN,求证:ABAE.
参考答案
一、选择题
题号 1 2 3 4 5
答案 D A B C A
1.【解答】解:∵四边形ABCD是平行四边形,ABBC=1,
∴AO=CO,BO=DO,AD=BC=2,AD∥BC,∠ABC=∠ADC=60°,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵AD∥BC,
∴∠DAE=∠AEB=∠BAE,∠DAC=∠ACB,
∴AB=BE=1,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AB=AE=BE=1,∠BAE=∠AEB=60°,
∴AE=EC=1,
∴∠ACB=∠EAC=30°,
∴∠CAD=30°,ACAB,故选项A不符合题意;
∴∠BAC=90°,AO=CO,
∴BO,
∴BD,故选项B不符合题意;
∵AO=CO,BE=CE=1,
∴OEAB,
∴OEAD,故选项C不符合题意;
∵S△ABCAB AC,AO=CO,BE=CE,
∴S△AOES△ABC,故选项D符合题意,
故选:D.
2.【解答】解:∵AB=3cm,BC=5cm,
∴2cm<AC<8cm,
∵四边形ABCD是平行四边形,
∴AOAC,
∴1cm<OA<4cm,
故选:A.
3.【解答】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP6,
∴△APB的周长=6+8+10=24;
故选:B.
4.【解答】解:①∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE=1,
∴△ABE是等边三角形,
∴AE=BE=1,
∵BC=2,
∴EC=1,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
故①正确;
②∵BE=EC,OA=OC,
∴OEAB,OE∥AB,
∴∠EOC=∠BAC=60°+30°=90°,
Rt△EOC中,OC,
∵四边形ABCD是平行四边形,
∴∠BCD=∠BAD=120°,
∴∠ACB=30°,
∴∠ACD=90°,
Rt△OCD中,OD,
∴BD=2OD,
故②错误;
③由②知:∠BAC=90°,
∴S平行四边形ABCD=AB AC,
故③正确;
④由②知:OE是△ABC的中位线,
∴OEAB,
∵ABBC,
∴OEBCAD,
故④正确;
故选:C.
5.【解答】解:过A作AM⊥BD交BD的延长线于M,AN⊥CE于N,
∵四边形BCED是平行四边形,
∴BD∥CE,BD=CE,
∴AM⊥CE,
∴M、A、N共线,
∵四边形ABFG是平行四边形,
∴FG∥AB,
∴△ABD的面积S1,
同理:△ACE的面积S2,
∴△ABD的面积+△ACE的面积(S1+S2),
∵△ABD的面积BD AM,△ACE的面积CE AN,
∴BD(AM+AN)=△ABD的面积+△ACE的面积(S1+S2),
∴BD MN=S1+S2,
∴平行四边形BCED的面积=S1+S2.
故选:A.
二、填空题
6.【解答】解:如图,把M、N拼在一起,得到平行四边形ABCD,则∠BCD=120°+α,
∵AB∥CD,
∴∠B=180°﹣∠BCD=180°﹣(120°+α)=60°﹣α,
∵四边形的内角和为360°,
∴70°+140°+120°+(60°﹣α)=360°,
∴α=30°,
故答案为:30.
7.【解答】解:设B点的坐标为(x,y),
∵平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),
∴,
解得x=3,y=﹣1,
∴B(3,﹣1).
故答案为:(3,﹣1).
8.【解答】解:当P点在BA上,BP=BE=6,
作BH⊥PE于H,如图1,则PH=EH,
∵∠B=120°,
∴∠BPE=∠BEP=30°,
在Rt△BEH中,BHBE=3,EHBH=3,
∴PE=2EH=6;
当P点在AD上,BP=PE,
作BG⊥AD于G,PF⊥BE于F,如图2,则BF=EF=3,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵∠ABC=120°,
∴∠A=60°,
在Rt△ABG中,AGAB=4,BGAG=4,
∴PF=4,
在Rt△PEF中,PE;
当点P在CD上,如图3,EB=EP=6,
综上所述,PE的长为6或6或.
故答案为6或6或.
9.【解答】解:如图,连接EF
∵△ADF与△DEF同底等高,
∴S△ADF=S△DEF,
即S△ADF﹣S△DPF=S△DEF﹣S△DPF,
即S△APD=S△EPF=17cm2,
同理可得S△BQC=S△EFQ=27cm2,
∴阴影部分的面积为S△EPF+S△EFQ=17+27=44cm2.
故答案为:44.
10.【解答】解:∵ ABCD的周长=2(BC+CD)=40,
∴BC+CD=20①,
∵AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,
∴S ABCD=4BC=6CD,
整理得,BCCD②,
联立①②解得,CD=8,
∴ ABCD的面积=AF CD=6CD=6×8=48.
故答案为:48.
三、解答题
11.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE∠ABC,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得:DF=CD,
∴AE=DF,
∴AE﹣EF=DF﹣EF,
∴AF=DE;
(2)解:∵AD=16,
∴AF+EF+DE=16,
∵AF=DE,EF=12,
∴AF+12+AF=16,
解得AF=2,
∴AB=AE=AF+EF=2+12=14,
∴ ABCD的周长为2(AB+AD)=2×(16+14)=60,即 ABCD的周长为60.
12.【解答】解:(1)平行四边形ABCD中,AB=4cm,AD=2cm
∴CD=AB=4cm,BC=AD=2cm
如图,过点B作BE⊥CD于点E,
∵∠C=30°
∴BEBC=1cm
∴平行四边形ABCD的面积为:CD×BE=4×1=4(cm2)
答:平行四边形ABCD的面积为4cm2.
(2)当t=0.5s时,
AP=2×0.5=1cm,AQ=1×0.5=0.5cm
如图,过点Q作QM⊥AP
∵四边形ABCD为平行四边形,
∴∠A=∠C
∵∠C=30°
∴∠A=30°
∴QMAQ0.5(cm)
∴△APQ的面积为:AP×QM1(cm2)
答:当t=0.5s时,△APQ的面积为(cm2).
(3)∵由(1)知平行四边形ABCD的面积为4cm2.
∴当△APQ的面积是平行四边形ABCD面积的时,
△APQ的面积为:4(cm2)
当点P在线段AB上运动t秒时,点Q在AD上运动t秒,AP=2tcm,AQ=tcm,高为cm
∴2t
∴t(舍)或t
∴t时符合题意;
当点P运动到线段BC上时,且运动时间为t秒时,点Q也运动到线段CD上,
如图,过点P作MN垂直CD于点M,垂直于AB延长线于点N
∵四边形ABCD为平行四边形,∠C=30°,
∴AB∥CD
∴∠PBN=∠C=30°
PNPB(2t﹣4)=(t﹣2)(cm),PM=1﹣(t﹣2)=(3﹣t)(cm)
S△APQ=44×(t﹣2)[4﹣(t﹣2)]×[1﹣(t﹣2)](t﹣2)×1
∴4﹣2t+4(6﹣t)(3﹣t)1
化简得:t2﹣4t+3=0
∴(t﹣1)(t﹣3)=0
∴t=1(不符合题意,舍)或t=3
当t=3时,点P位于点C处,点Q位于线段CD上,符合题意.
综上,t的值为或3.
13.【解答】(1)证明:∵平行四边形ABCD,
∴AB=CD,OA=OC,AB∥CD,
∴∠BAE=∠DCF,
∵点E,F分别为OA,OC的中点,
∴,,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:∵BD=2AB,且AB=20,CF=12,
∴BD=40,
∵四边形ABCD是平行四边形,
∴,
∴△DCO为等腰三角形,
∵点F是CO的中点,
∴DF⊥AC,
在Rt△CDF中,CF=12,CD=20,
由勾股定理得:.
14.【解答】(1)解:∵点E为BC的中点,
∴BC=2BE,
由条件可知AE=BC,
∵四边形ABCD是平行四边形,AD=4,
∴AD=BC=4,
∴AE=AD=4,,
∵AE⊥BC,
∴AB2;
(2)证明:过点A作AH⊥AF交DP于点H,
则∠DAE=∠FAH=90°,
∴∠DAE﹣∠EAH=∠FAH﹣∠EAH,
即∠DAH=∠EAF,
∵∠1+∠EAD+∠ADP=180°,∠2+∠EFD+∠AEF=180°,
且∠1=∠2,∠DAE=∠EFD=90°,
∴∠AEF=∠ADF,
∵∠DAH=∠EAF,AD=AE,
∴△AEF≌△ADH(ASA),
∴DH=EF,AF=AH,
在Rt△AFH中,∠FAH=90°,
由勾股定理得:,
∵DF=FH+HD,
∴,
∴.
15.【解答】(1)解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠CAD=∠ACB=∠BCN=60°,
又AC⊥CD,
∴AB⊥AC,
∴∠B=30°,
在Rt△ABC中,E为BC的中点,
∴BC=2AE=10,
∴ACBC=5,
∴,
∴;
(2)证明:延长CN至G,使CG=AC,
由(1)知∠ACM=∠GCM,
又MC=MC,
∴△ACM≌△GCM,
∴AM=GM,∠MAC=∠G,
又AM=MN,
∴GM=MN,
∴∠G=∠MNG=∠MAC=∠MAE+∠EAC,
又由(1)可得EC=EA,
∴∠EAC=∠ACE=∠NCM,
∵∠MNG=∠NCM+∠NMC,
∴∠NMC=∠MAE,
在MC上截取MF=AE,
∴△MAE≌△NMF,
∴ME=FN,
又MC=ME+CE=MF+CF,MC=EA+CN,
∵EA=MF=CE,
∴ME=CN=FN=CF,
∴△NCF为等边三角形,
∴∠MCN=60°,
∴∠ACB=60°,
∴∠ABC=30°,
∴,
∵AEBC,
∴ABAE.
21世纪教育网(www.21cnjy.com)
4.2平行四边形及其性质培优练习浙教版2024—2025学年八年级下册
一、选择题
1.如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,,下列结论中,不正确的是( )
A.∠CAD=30° B.BD
C.OE D.
2.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.1cm<OA<4cm B.2cm<OA<8cm
C.2cm<OA<5cm D.3cm<OA<8cm
3.如图,在平行四边形ABCD中P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是( )
A.18 B.24 C.23 D.14
4.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E、P.连接OE,∠ADC=60°,ABBC=1,则下列结论:
①∠CAD=30°;②BD=2;③S平行四边形ABCD=AB AC;④AD=4OE.
其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,分别以△ABC的三边为一边作 BCED, ABFG, ACIH,且点D,E分别在FG,HI上.若 ABFG, ACIH的面积分别为S1,S2,则 BCED的面积为( )
A.S1+S2 B. C. D.
二、填空题
6.如图,平移图形M,与图形N可以拼成一个平行四边形,则图中∠α= °.
7.如图,在平面直角坐标系中,平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),则顶点B的坐标为 .
8.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为 .
9.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=17cm2,S△BQC=27cm2,则阴影部分的面积为 cm2.
10.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6, ABCD的周长为40,则 ABCD的面积为 .
三、解答题
11.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G.
(1)求证:AF=DE.
(2)若AD=16,EF=12,请求出 ABCD的周长.
12.如图,平行四边形ABCD中,AB=4cm,AD=2cm,∠C=30°.点P以2cm/s的速度从顶点A出发沿折线A﹣B﹣C向点C运动,同时点Q以1cm/s的速度从顶点A出发沿折线A﹣D﹣C向点C运动,当其中一个动点到达末端停止运动时,另一点也停止运动.设运动时间为ts.
(1)求平行四边形ABCD的面积;
(2)求当t=0.5s时,△APQ的面积;
(3)当△APQ的面积是平行四边形ABCD面积的时,求t的值.
13.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=20,CF=12,求DF的长.
14.如图,在平行四边形ABCD中,AE⊥BC于点E,点E为BC的中点,AE=2BE.点P在BE上,作EF⊥DP于点F,连接AF.
(1)若AD=4,求AB的长;
(2)求证:.
15.在平行四边形ABCD中,AC⊥CD,E为BC中点,点M在线段BE上,连接AM,在BC下方有一点N,满足∠CAD=∠BCN,连接MN.
(1)若∠BCN=60°,AE=5,求△ABE的面积;
(2)若MA=MN,MC=EA+CN,求证:ABAE.
参考答案
一、选择题
题号 1 2 3 4 5
答案 D A B C A
1.【解答】解:∵四边形ABCD是平行四边形,ABBC=1,
∴AO=CO,BO=DO,AD=BC=2,AD∥BC,∠ABC=∠ADC=60°,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵AD∥BC,
∴∠DAE=∠AEB=∠BAE,∠DAC=∠ACB,
∴AB=BE=1,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AB=AE=BE=1,∠BAE=∠AEB=60°,
∴AE=EC=1,
∴∠ACB=∠EAC=30°,
∴∠CAD=30°,ACAB,故选项A不符合题意;
∴∠BAC=90°,AO=CO,
∴BO,
∴BD,故选项B不符合题意;
∵AO=CO,BE=CE=1,
∴OEAB,
∴OEAD,故选项C不符合题意;
∵S△ABCAB AC,AO=CO,BE=CE,
∴S△AOES△ABC,故选项D符合题意,
故选:D.
2.【解答】解:∵AB=3cm,BC=5cm,
∴2cm<AC<8cm,
∵四边形ABCD是平行四边形,
∴AOAC,
∴1cm<OA<4cm,
故选:A.
3.【解答】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP6,
∴△APB的周长=6+8+10=24;
故选:B.
4.【解答】解:①∵AE平分∠BAD,
∴∠BAE=∠DAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC=∠ADC=60°,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE=1,
∴△ABE是等边三角形,
∴AE=BE=1,
∵BC=2,
∴EC=1,
∴AE=EC,
∴∠EAC=∠ACE,
∵∠AEB=∠EAC+∠ACE=60°,
∴∠ACE=30°,
∵AD∥BC,
∴∠CAD=∠ACE=30°,
故①正确;
②∵BE=EC,OA=OC,
∴OEAB,OE∥AB,
∴∠EOC=∠BAC=60°+30°=90°,
Rt△EOC中,OC,
∵四边形ABCD是平行四边形,
∴∠BCD=∠BAD=120°,
∴∠ACB=30°,
∴∠ACD=90°,
Rt△OCD中,OD,
∴BD=2OD,
故②错误;
③由②知:∠BAC=90°,
∴S平行四边形ABCD=AB AC,
故③正确;
④由②知:OE是△ABC的中位线,
∴OEAB,
∵ABBC,
∴OEBCAD,
故④正确;
故选:C.
5.【解答】解:过A作AM⊥BD交BD的延长线于M,AN⊥CE于N,
∵四边形BCED是平行四边形,
∴BD∥CE,BD=CE,
∴AM⊥CE,
∴M、A、N共线,
∵四边形ABFG是平行四边形,
∴FG∥AB,
∴△ABD的面积S1,
同理:△ACE的面积S2,
∴△ABD的面积+△ACE的面积(S1+S2),
∵△ABD的面积BD AM,△ACE的面积CE AN,
∴BD(AM+AN)=△ABD的面积+△ACE的面积(S1+S2),
∴BD MN=S1+S2,
∴平行四边形BCED的面积=S1+S2.
故选:A.
二、填空题
6.【解答】解:如图,把M、N拼在一起,得到平行四边形ABCD,则∠BCD=120°+α,
∵AB∥CD,
∴∠B=180°﹣∠BCD=180°﹣(120°+α)=60°﹣α,
∵四边形的内角和为360°,
∴70°+140°+120°+(60°﹣α)=360°,
∴α=30°,
故答案为:30.
7.【解答】解:设B点的坐标为(x,y),
∵平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),
∴,
解得x=3,y=﹣1,
∴B(3,﹣1).
故答案为:(3,﹣1).
8.【解答】解:当P点在BA上,BP=BE=6,
作BH⊥PE于H,如图1,则PH=EH,
∵∠B=120°,
∴∠BPE=∠BEP=30°,
在Rt△BEH中,BHBE=3,EHBH=3,
∴PE=2EH=6;
当P点在AD上,BP=PE,
作BG⊥AD于G,PF⊥BE于F,如图2,则BF=EF=3,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵∠ABC=120°,
∴∠A=60°,
在Rt△ABG中,AGAB=4,BGAG=4,
∴PF=4,
在Rt△PEF中,PE;
当点P在CD上,如图3,EB=EP=6,
综上所述,PE的长为6或6或.
故答案为6或6或.
9.【解答】解:如图,连接EF
∵△ADF与△DEF同底等高,
∴S△ADF=S△DEF,
即S△ADF﹣S△DPF=S△DEF﹣S△DPF,
即S△APD=S△EPF=17cm2,
同理可得S△BQC=S△EFQ=27cm2,
∴阴影部分的面积为S△EPF+S△EFQ=17+27=44cm2.
故答案为:44.
10.【解答】解:∵ ABCD的周长=2(BC+CD)=40,
∴BC+CD=20①,
∵AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,
∴S ABCD=4BC=6CD,
整理得,BCCD②,
联立①②解得,CD=8,
∴ ABCD的面积=AF CD=6CD=6×8=48.
故答案为:48.
三、解答题
11.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE∠ABC,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得:DF=CD,
∴AE=DF,
∴AE﹣EF=DF﹣EF,
∴AF=DE;
(2)解:∵AD=16,
∴AF+EF+DE=16,
∵AF=DE,EF=12,
∴AF+12+AF=16,
解得AF=2,
∴AB=AE=AF+EF=2+12=14,
∴ ABCD的周长为2(AB+AD)=2×(16+14)=60,即 ABCD的周长为60.
12.【解答】解:(1)平行四边形ABCD中,AB=4cm,AD=2cm
∴CD=AB=4cm,BC=AD=2cm
如图,过点B作BE⊥CD于点E,
∵∠C=30°
∴BEBC=1cm
∴平行四边形ABCD的面积为:CD×BE=4×1=4(cm2)
答:平行四边形ABCD的面积为4cm2.
(2)当t=0.5s时,
AP=2×0.5=1cm,AQ=1×0.5=0.5cm
如图,过点Q作QM⊥AP
∵四边形ABCD为平行四边形,
∴∠A=∠C
∵∠C=30°
∴∠A=30°
∴QMAQ0.5(cm)
∴△APQ的面积为:AP×QM1(cm2)
答:当t=0.5s时,△APQ的面积为(cm2).
(3)∵由(1)知平行四边形ABCD的面积为4cm2.
∴当△APQ的面积是平行四边形ABCD面积的时,
△APQ的面积为:4(cm2)
当点P在线段AB上运动t秒时,点Q在AD上运动t秒,AP=2tcm,AQ=tcm,高为cm
∴2t
∴t(舍)或t
∴t时符合题意;
当点P运动到线段BC上时,且运动时间为t秒时,点Q也运动到线段CD上,
如图,过点P作MN垂直CD于点M,垂直于AB延长线于点N
∵四边形ABCD为平行四边形,∠C=30°,
∴AB∥CD
∴∠PBN=∠C=30°
PNPB(2t﹣4)=(t﹣2)(cm),PM=1﹣(t﹣2)=(3﹣t)(cm)
S△APQ=44×(t﹣2)[4﹣(t﹣2)]×[1﹣(t﹣2)](t﹣2)×1
∴4﹣2t+4(6﹣t)(3﹣t)1
化简得:t2﹣4t+3=0
∴(t﹣1)(t﹣3)=0
∴t=1(不符合题意,舍)或t=3
当t=3时,点P位于点C处,点Q位于线段CD上,符合题意.
综上,t的值为或3.
13.【解答】(1)证明:∵平行四边形ABCD,
∴AB=CD,OA=OC,AB∥CD,
∴∠BAE=∠DCF,
∵点E,F分别为OA,OC的中点,
∴,,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:∵BD=2AB,且AB=20,CF=12,
∴BD=40,
∵四边形ABCD是平行四边形,
∴,
∴△DCO为等腰三角形,
∵点F是CO的中点,
∴DF⊥AC,
在Rt△CDF中,CF=12,CD=20,
由勾股定理得:.
14.【解答】(1)解:∵点E为BC的中点,
∴BC=2BE,
由条件可知AE=BC,
∵四边形ABCD是平行四边形,AD=4,
∴AD=BC=4,
∴AE=AD=4,,
∵AE⊥BC,
∴AB2;
(2)证明:过点A作AH⊥AF交DP于点H,
则∠DAE=∠FAH=90°,
∴∠DAE﹣∠EAH=∠FAH﹣∠EAH,
即∠DAH=∠EAF,
∵∠1+∠EAD+∠ADP=180°,∠2+∠EFD+∠AEF=180°,
且∠1=∠2,∠DAE=∠EFD=90°,
∴∠AEF=∠ADF,
∵∠DAH=∠EAF,AD=AE,
∴△AEF≌△ADH(ASA),
∴DH=EF,AF=AH,
在Rt△AFH中,∠FAH=90°,
由勾股定理得:,
∵DF=FH+HD,
∴,
∴.
15.【解答】(1)解:∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠CAD=∠ACB=∠BCN=60°,
又AC⊥CD,
∴AB⊥AC,
∴∠B=30°,
在Rt△ABC中,E为BC的中点,
∴BC=2AE=10,
∴ACBC=5,
∴,
∴;
(2)证明:延长CN至G,使CG=AC,
由(1)知∠ACM=∠GCM,
又MC=MC,
∴△ACM≌△GCM,
∴AM=GM,∠MAC=∠G,
又AM=MN,
∴GM=MN,
∴∠G=∠MNG=∠MAC=∠MAE+∠EAC,
又由(1)可得EC=EA,
∴∠EAC=∠ACE=∠NCM,
∵∠MNG=∠NCM+∠NMC,
∴∠NMC=∠MAE,
在MC上截取MF=AE,
∴△MAE≌△NMF,
∴ME=FN,
又MC=ME+CE=MF+CF,MC=EA+CN,
∵EA=MF=CE,
∴ME=CN=FN=CF,
∴△NCF为等边三角形,
∴∠MCN=60°,
∴∠ACB=60°,
∴∠ABC=30°,
∴,
∵AEBC,
∴ABAE.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
