4.1多边形培优练习（含答案）

中小学教育资源及组卷应用平台
4.1多边形培优练习浙教版2024—2025学年八年级下册
一、选择题
1．如图，Rt△ABC的两条直角边AC，BC分别经过正五边形的两个顶点，则∠1+∠2等于（　 ）
A．126° B．130° C．136° D．140°
2．如图，在四边形ABCD中，∠DAB的角平分线与∠ABC的外角平分线相交于点P，且∠D+∠C＝210°，则∠P＝（　　）
A．10° B．15° C．30° D．40°
3．如图，∠A+∠B+∠C+∠D+∠E的度数为（　　）
A．180° B．240° C．270° D．360°
4．若一个多边形截去一个角后变成了六边形，则原来多边形的边数可能是（　　）
A．5或6 B．6或7 C．5或6或7 D．6或7或8
5．如图，∠B+∠C+∠D+∠E﹣∠A等于（　　）
A．180° B．240° C．300° D．360°
二、填空题
6．如图所示，将正六边形与正五边形按此方式摆放，正六边形与正五边形的公共顶点为O，且正六边形的边AB与正五边形的边DE在同一条直线上，则∠COF的度数为 　 　．
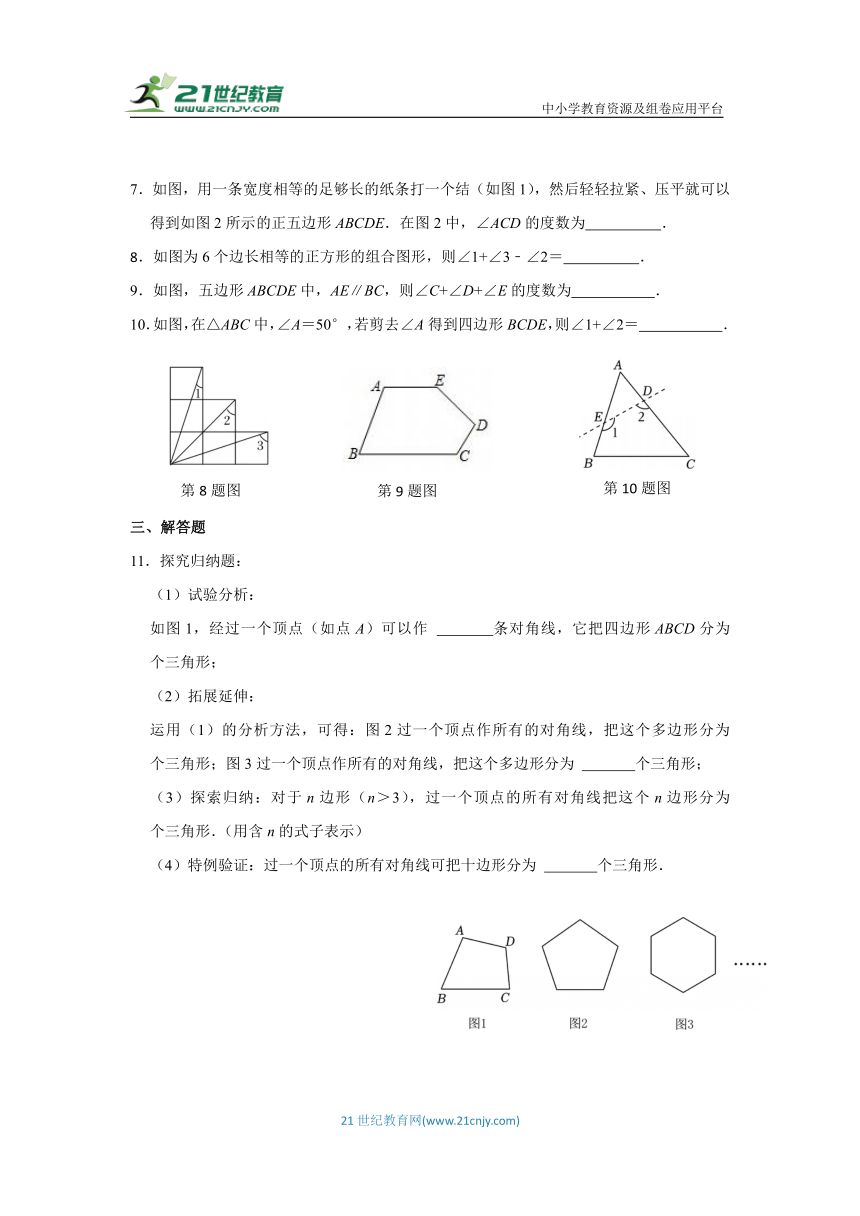
7．如图，用一条宽度相等的足够长的纸条打一个结（如图1），然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE．在图2中，∠ACD的度数为　 　．
8．如图为6个边长相等的正方形的组合图形，则∠1+∠3﹣∠2＝　 　．
9．如图，五边形ABCDE中，AE∥BC，则∠C+∠D+∠E的度数为　 　．
10．如图，在△ABC中，∠A＝50°，若剪去∠A得到四边形BCDE，则∠1+∠2＝　 　．
三、解答题
11．探究归纳题：
（1）试验分析：
如图1，经过一个顶点（如点A）可以作 　 　条对角线，它把四边形ABCD分为 　 　个三角形；
（2）拓展延伸：
运用（1）的分析方法，可得：图2过一个顶点作所有的对角线，把这个多边形分为 　 　个三角形；图3过一个顶点作所有的对角线，把这个多边形分为 　 　个三角形；
（3）探索归纳：对于n边形（n＞3），过一个顶点的所有对角线把这个n边形分为 　 　个三角形．（用含n的式子表示）
（4）特例验证：过一个顶点的所有对角线可把十边形分为 　 　个三角形．
12．如图，四边形ABCD，BE、DF分别平分四边形的外角∠MBC和∠NDC，若∠BAD＝α，∠BCD＝β．
（1）如图1，若α+β＝105°，求∠MBC+∠NDC的度数；
（2）如图1，若BE与DF相交于点G，∠BGD＝45°，请直接写出α，β所满足的数量关系式；
（3）如图2，若α＝β，判断BE，DF的位置关系，并说明理由．
13．探究一：
（1）如图1，在△ABC中，∠A＝64°，BP，CP分别是两个内角∠ABC，∠ACB的角平分线，则∠P＝　 　度．
（2）如图2，在△ABC中，∠A＝70°，BP，CP分别是两个外角∠CBD，∠BCE的角平分线，则∠P＝　 　度．
探究二：（1）如图3，在△ABC中，BP是三角形内角∠ABC的角平分线，CP是外角∠ACD的角平分线．请说明∠P和∠A之间的数量关系？并证明你的结论．
（2）如图4，在四边形ABCD中，BP是内角∠ABC的角平分线，CP是外角∠DCE的角平分线，请直接写出∠P与∠A，∠D之间的数量关系．（不用说明理由）
14．如图，AB⊥CD，垂足为O，点P、Q分别在射线OC、OA上运动（点P、Q都不与点O重合），QE是∠AQP的平分线．
（1）如图1，在点P、Q的运动过程中，若直线QE交∠DPQ的平分线于点H．
①当∠PQB＝60°时，∠PHE＝　 　°；
②随着点P、Q分别在OC、OA的运动，∠PHE的大小是否是定值？如果是定值，请求出∠PHE的度数；如果不是定值，请说明理由；
（2）如图2，若QE所在直线交∠QPC的平分线于点E时，将△EFG沿FG折叠，使点E落在四边形PFGQ内点E′的位置，猜测∠PFE′与∠QGE′之间的数量关系，并说明理由．
15．如图，在四边形ABCD中，∠A＝x，∠C＝y．
（1）∠ABC+∠ADC＝　 　（用含x，y的式子直接填空）；
（2）如图1，若x＝y＝90°，DE平分∠ADC，BF平分∠CBM，请写出DE与BF的位置关系，并说明理由；
（3）如图2，∠DFB为四边形ABCD的∠ABC，∠ADC相邻的外角平分线所在直线构成的锐角．若x+y＝120°，∠DFB＝20°，求x，y的值．
参考答案
一、选择题
题号 1 2 3 4 5
答案 A B A C A
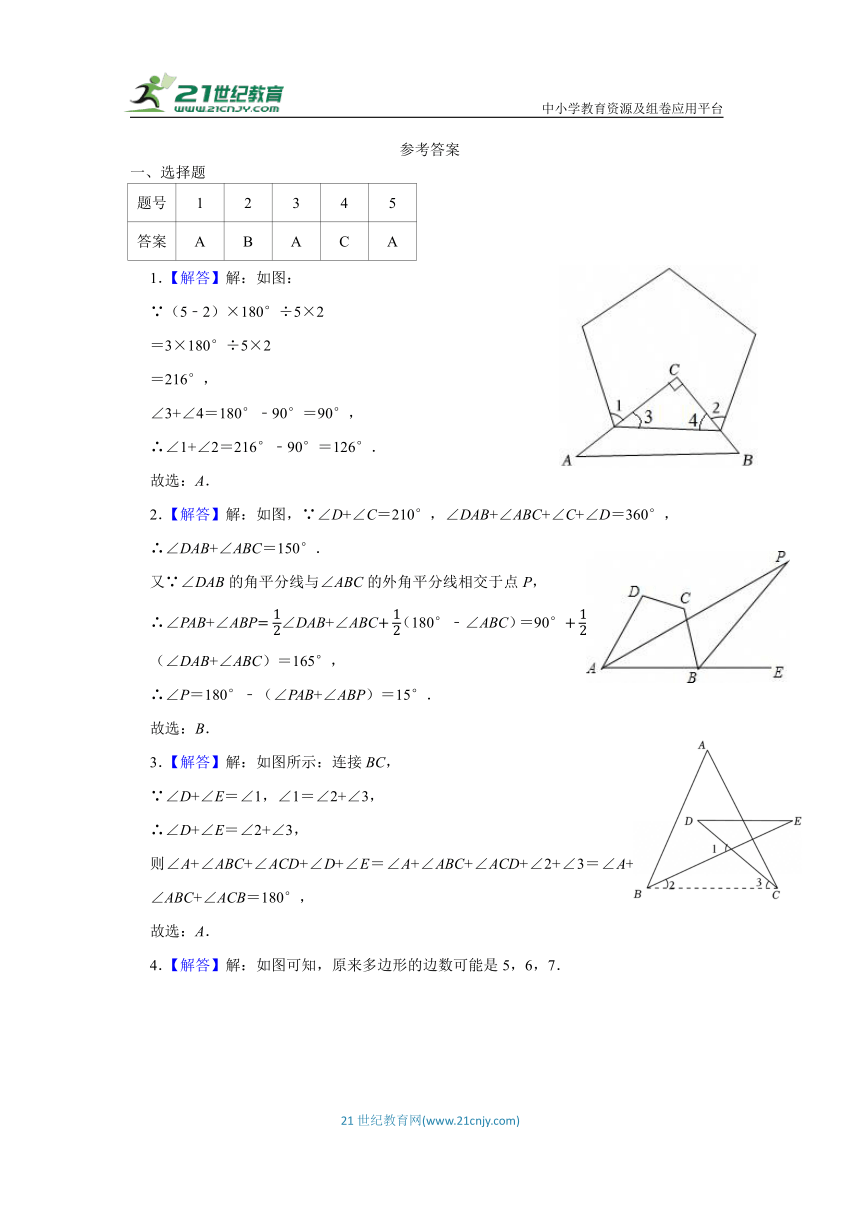
1．【解答】解：如图：
∵（5﹣2）×180°÷5×2
＝3×180°÷5×2
＝216°，
∠3+∠4＝180°﹣90°＝90°，
∴∠1+∠2＝216°﹣90°＝126°．
故选：A．
2．【解答】解：如图，∵∠D+∠C＝210°，∠DAB+∠ABC+∠C+∠D＝360°，
∴∠DAB+∠ABC＝150°．
又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P，
∴∠PAB+∠ABP∠DAB+∠ABC（180°﹣∠ABC）＝90°（∠DAB+∠ABC）＝165°，
∴∠P＝180°﹣（∠PAB+∠ABP）＝15°．
故选：B．
3．【解答】解：如图所示：连接BC，
∵∠D+∠E＝∠1，∠1＝∠2+∠3，
∴∠D+∠E＝∠2+∠3，
则∠A+∠ABC+∠ACD+∠D+∠E＝∠A+∠ABC+∠ACD+∠2+∠3＝∠A+∠ABC+∠ACB＝180°，
故选：A．
4．【解答】解：如图可知，原来多边形的边数可能是5，6，7．
故选：C．
5．【解答】解：根据三角形的外角的性质，得∠B+∠C＝∠CGE＝180°﹣∠AGF，∠D+∠E＝∠DFG＝180°﹣∠AFG，两式相加再减去∠A，根据三角形的内角和是180°可求解．
∵∠B+∠C＝∠CGE＝180°﹣∠ADF，∠D+∠E＝∠DFG＝180°﹣∠AFG，
∴∠B+∠C+∠D+∠E﹣∠A＝360°﹣（∠AGF+∠AFG+∠A）＝180°．
故答案为：A．
二、填空题
6．【解答】解：由题意得：∠EOF＝108°，∠BOC＝120°，∠OEB＝72°，∠OBE＝60°，
∴∠BOE＝180°﹣72°﹣60°＝48°，
∴∠COF＝360°﹣108°﹣48°﹣120°＝84°，
故答案为：84°．
7．【解答】解：∵五边形ABCDE是正五边形，
∴其每个内角为108°，且AB＝BC，
∴△ABC是等腰三角形，
∴∠BCA＝（180°﹣108°）÷2＝36°，
∴∠ACD＝∠BCE﹣∠BCA＝108°﹣36°＝72°．
故答案为：72°
8．【解答】解：如图：
在△ABC和△DEA中，
，
∴△ABC≌△DEA（SAS），
∴∠1＝∠4，
∵∠3+∠4＝90°，
∴∠1+∠3＝90°，
又∵∠2＝45°，
∴∠1+∠3﹣∠2＝90°﹣45°＝45°．
故答案为：45°．
9．【解答】解：过点D作DF∥AE，交AB于点F，
∵AE∥BC，
∴AE∥DF∥BC，
∴∠A+∠B＝180°，∠E+∠EDF＝180°，∠CDF+∠C＝180°，
∴∠C+∠CDE+∠E＝360°，
故答案为360°．
10．【解答】解：∵△ABC中，∠A＝50°，
∴∠B+∠C＝180°﹣50°＝130°，
∵∠B+∠C+∠1+∠2＝360°，
∴∠1+∠2＝360°﹣130°＝230°．
故答案为：230°．
三、解答题
11．【解答】解：（1）如图1，经过一个顶点（如点A）可以作1条对角线，它把四边形ABCD分为2个三角形；
（2）应用（1）的分析方法，可得：图2过一个顶点作所有的对角线，把这个多边形分为3个三角形；图3过一个顶点作所有的对角线，把这个多边形分为4个三角形；
（3）对于n边形（n＞3），过一个顶点的所有对角线把这个n边形分为（n﹣2）个三角形．（用含n的式子表示）；
（4）过一个顶点的所有对角线可把十边形分为8个三角形．
故答案为：（1）1，2；（2）3，4；（3）（n﹣2）；（4）8．
12．【解答】解：（1）∵四边形ABCD的内角和为360°，
∴α+β＝∠A+∠BCD＝360°﹣（∠ABC+∠ADC），
∵∠MBC和∠NDC是四边形ABCD的外角，
∴∠MBC＝180°﹣∠ABC，∠NDC＝180°﹣∠ADC，
∴∠MBC+∠NDC＝180°﹣∠ABC+180°﹣∠ADC
＝360°﹣（∠ABC+∠ADC），
＝α+β
＝105°；
（2）β﹣α＝90°（或α﹣β＝﹣90°等均正确）．
理由：如图1，连接BD，
由（1）有，∠MBC+∠NDC＝α+β，
∵BE、DF分别平分四边形的外角∠MBC和∠NDC，
∴∠CBG∠MBC，∠CDG∠NDC，
∴∠CBG+∠CDG∠MBC∠NDC（∠MBC+∠NDC）（α+β），
在△BCD中，∠BDC+∠CBD＝180°﹣∠BCD＝180°﹣β，
在△BDG中，∠BGD＝45°，∠GBD+∠GDB+∠BGD＝180°，
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD＝180°，
∴（∠CBG+∠CDG）+（∠BDC+∠CBD）+∠BGD＝180°，
∴（α+β）+180°﹣β+45°＝180°，
∴β﹣α＝90°．
（3）BE∥DF．
理由：如图2，过点C作CP∥BE，
则∠EBC＝∠BCP，
∴∠DCP＝∠BCD﹣∠BCP＝β﹣∠EBC，
由（1）知∠MBC+∠NDC＝α+β，
∵α＝β，
∴∠MBC+∠NDC＝2β，
又∵BE、DF分别平分∠MBC和∠NDC，
∴∠EBC+∠FDC（∠MBC+∠NDC）＝β，
∴∠FDC＝β﹣∠EBC，
又∵∠DCP＝β﹣∠EBC，
∴∠FDC＝∠DCP，
∴CP∥DF，
又CP∥BE，
∴BE∥DF．
13．【解答】解：探究一：
（1）如图1，∵∠A＝64°，∠A+∠ABC+∠ACB＝180°，
∴∠ABC+∠ACB＝116°，
∵BP，CP分别平分∠ABC，∠ACB，
∴∠PBC∠ABC，∠PCB∠ACB，
∴∠PBC+∠PCB（∠ABC+∠ACB）116°＝58°，
∵∠P+∠PBC+∠PCB＝180°，
∴∠P＝180°﹣58°＝122°，
故答案为：122．
（2）如图2，∵∠A＝70°，∠A+∠ABC+∠ACB＝180°，
∴∠ABC+∠ACB＝110°，
∵BP，CP分别平分∠DBC，∠ECB，
∴∠PBC∠DBC，∠PCB∠ECB，
∴∠PBC+∠PCB（∠DBC+∠ECB）
（180°﹣∠ABC+180°﹣∠ACB）
＝180°（∠ABC+∠ACB）
＝180°110°
＝125°，
∴∠P＝180°﹣（∠PBC+∠PCB）＝180°﹣125°＝55°，
故答案为：55．
探究二：
（1）∠A＝2∠P．理由如下：
如图3，∵BP是△ABC中∠ABC的平分线，CP是外角∠ACD的角平分线，
∴∠PBC∠ABC，∠PCD∠ACD，
∵∠ACD是△ABC的外角，∠PCD是△BPC的外角，
∴∠ACD＝∠ABC+∠A，∠PCD＝∠PBC+∠P，
∴∠ACD∠ABC∠A，
∴∠ABC∠A＝∠PBC+∠P，
∴∠A＝2∠P；
（2）∠P（∠A+∠D）﹣90°．理由如下：
如图4，由四边形内角和定理得∠BCD＝360°﹣∠A﹣∠D﹣∠ABC，
∴∠DCE＝180°﹣（360°﹣∠A﹣∠D﹣∠ABC）＝∠A+∠D+∠ABC﹣180°，
由三角形的外角性质得，∠PCE＝∠P+∠PBC，
∵BP、CP分别是∠ABC和∠DCE的平分线，
∴∠PBC∠ABC，∠PCE∠DCE，
∴∠P+∠PBC（∠A+∠D+∠ABC﹣180°）（∠A+∠D）∠ABC﹣90°，
∴∠P（∠A+∠D）﹣90°．
14．【解答】解：（1）①∵AB⊥CD，
∴∠POQ＝90°，
∴∠PQO+∠QPO＝90°，
∵∠PQB＝60°，
∴∠QPO＝30°，∠AQP＝120°，
∵EQ平分∠AQP，PH平分∠QPO，
∴，，
∴∠H＝∠EQP﹣∠HPQ＝45°，
故答案为：45；
②∠PHE 是一个定值，∠PHE＝45°，理由如下：
∵AB⊥CD，
∴∠POQ＝90°，
∴∠PQO+∠QPO＝90°，
∴∠QPO＝90°﹣∠PQO，∠AQP＝180°﹣∠PQO，
∵EQ平分∠AQP，PH平分∠QPO，
∴，，
∴∠H＝∠EQP﹣∠HPQ＝45°；
（2）∠PFE'+∠QGE'＝90°，理由如下：
如图2所示，连接EE'，
∵AB⊥CD，
∴∠POQ＝90°，
∴∠PQO+∠QPO＝90°，
∵∠CPQ+∠QPO＝180°，∠PQA+∠PQO＝180°，
∴180°﹣∠CPQ+180°﹣∠PQA＝90°，
∴∠CPQ+∠PQA＝270°，
∵QE，PE分别平分∠PQA，∠CPQ，
∴，
∴，
∴∠PEQ＝180°﹣∠EPQ﹣∠EQP＝45°，
由折叠的性质可知∠GE'F＝∠PEQ＝45°，
∵∠FEE'+∠EFE'+∠EE'F＝180°＝∠GEE'+∠EGE'+∠EE'G，
∴∠FEG+∠FE'G+∠EFE'+∠EGE'＝360°，
∴∠EFE'+∠EFE'＝270°，
∵∠EFE'+∠PFE'＝180°＝∠EGE'+∠QGE'，
∴∠PFE'+∠QGE'＝360°﹣∠EFE'﹣∠EFE'＝90°．
15．【解答】解：（1）∵∠A+∠ABC+∠C+∠ADC＝360°，∠A＝x，∠C＝y，
∴∠ABC+∠ADC＝360°﹣x﹣y；
故答案为：360°﹣x﹣y；
（2）DE⊥BF．
理由：如图1：
∵DE平分∠ADC，BF平分∠MBC，
∴∠CDE∠ADC，∠CBF∠CBM，
又∵∠CBM＝180°﹣∠ABC＝180°﹣（180°﹣∠ADC）＝∠ADC，
∴∠CDE＝∠CBF，
又∵∠DGC＝∠BGE，
∴∠BEG＝∠C＝90°，
∴DE⊥BF；
（3）由（1）得：∠CDN+∠CBM＝360°﹣（360°﹣x﹣y）＝x+y，
∵BF、DF分别平分∠CBM、∠CDN，
∴∠CDF+∠CBF（x+y），
如图2，连接DB，则∠CBD+∠CDB＝180°﹣y，
∴∠FBD+∠FDB＝180°﹣y（x+y）＝180°yx，
∴∠DFByx＝20°，
解方程组：，
可得：，
即x＝40°，y＝80°．
21世纪教育网(www.21cnjy.com)