第三章数据分析初步(A卷)单元测试(含答案)
文档属性
| 名称 | 第三章数据分析初步(A卷)单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 488.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-10 22:02:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章数据分析初步(A卷)单元测试浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.甲、乙、丙、丁四位学生参加立定跳远训练,他们近期5次训练的平均成绩相同,设甲、乙、丙、丁这5次训练成绩的方差分别是S甲2,S乙2,S丙2,S丁2,且S甲2=2.1,S乙2=3.5,S丙2=5.6,S丁2=0.9,则四位学生中这5次训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.为贯彻落实教育部《关于全面加强新时代大中小学劳动教育的意见》精神,把劳动教育纳入人才培养全过程,某校组织学生周末赴劳动教育实践基地开展锄地、除草、浇水、剪枝、捉鱼、采摘六项实践活动,已知六个项目参与人数(单位:人)分别是:35,38,40,42,42,43.则这组数据的众数和中位数分别是( )
A.38,39 B.42,40 C.42,41 D.42,42
3.某校篮球队5名场上队员的身高是182,188,190,190,192(单位:cm),现用两名身高分别为186cm和190cm的队员换下场上两名身高是182cm和192cm的队员,下列关于换人前后场上队员的身高说法正确的为( )
A.中位数变大,众数不变 B.中位数不变,方差变小
C.平均数变大,众数变小 D.平均数变小,方差变大
4.老师在黑板上写出一个计算方差的算式:,根据上式还原得到的数据,下列结论不正确的是( )
A.n=5 B.平均数为8
C.添加一个数8后方差不变 D.这组数据的众数是6
5.若从一组数据2,4,6,8,10中去掉一个最大数和一个最小数,则所得新数据与原数据相比( )
A.平均数不变,方差变小 B.平均数不变,方差变大
C.平均数变小,方差变小 D.平均数变小,方差变大
6.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.中位数 B.众数 C.平均数 D.方差
7.某校竞选学生会主席分为现场演讲和答辩两个环节,其中现场演讲分占80%,答辩分占20%,小明参加并在这两个环节中分别取得85分和90分的成绩,则小明的最终成绩为( )
A.80分 B.84分 C.86分 D.88分
8.如果一组数据x1,x2,…x5的平均数是2,方差是2,则另一组数据3x1﹣2,3x2﹣2,3x3﹣2,…3x5﹣2的平均数和方差分别是( )
A.2,2 B.2,6 C.4,4 D.4,18
二.填空题(每小题5分,满分20分)
9.学校举行篮球技能大赛,评委从控球技能、投球技能、身体素质三方面为选手打分,各项成绩均按百分制计,然后再按控球技能占30%、投球技能占30%、身体素质占40%计算选手的综合成绩(百分制).选手张少能控球技能得90分,投球技能得80分,身体素质得85分,则张少能的综合成绩为 .
10.一组数据的方差计算为:,则这组数据的平均数为 .
11.已知两组数据x1,x2,……,xn和y1,y2,……,yn的平均数分别为5和﹣2,则x1+2y1,x2+2y2,……,xn+2yn的平均数为 .
12.小明同学用手机软件记录了5月份每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,中位数是 万步.
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.求实中学积极落实“双减”政策,扎实有效地开展了多项体育运动.本学期七年级学生在体育老师的组织下开展了一次定点投篮比赛,如下表为七年级某班48人参加定点投篮比赛的情况记录,若标准数量为每人三分钟定点投篮投中25个.
定点投篮投中个数与标准数量的差值 ﹣11 ﹣6 0 8 10
人数 5 12 10 6 10
(1)该班平均每人三分钟定点投篮投中多少个?
(2)规定定点投篮投中个数达到标准数量记0分,超过标准数量,每多投1个加2分,每少投1个扣1分,求该班定点投篮总共获得多少分?
14.某校七、八年级开展了一次综合实践知识竞赛,按10分制进行评分,成绩(单位:分)均为不低于6的整数.为了解这次活动的效果,现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理,并绘制成统计图表,部分信息如下:
八年级10名学生活动成绩统计表
成绩(分) 6 7 8 9 10
人数 1 2 a b 2
已知八年级10名学生成绩的中位数为8.5分.
请根据以上信息,解答下列问题:
(1)样本中,七年级活动成绩为7分的学生数是 ,七年级活动成绩的众数为 分.
(2)a= ,b= .
(3)若认定活动成绩不低于9分为“优秀”,则根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
15.某校甲、乙两个班级各有23名学生进行校运动会入场式的队列训练,为了解这两个班级参加队列训练的学生的身高情况,测量并获取了这些学生的身高(单位:cm),数据整理如下:
a.甲班23名学生的身高:
163,163,164,165,165,166,166,166,166,167,167,168,169,169,170,171,171,172,173,173,174,179,180.
b.两班学生身高的平均数、中位数、众数如表所示:
班级 平均数 中位数 众数
甲 169 m n
乙 169 170 167
(1)写出表中m,n的值;
(2)在甲班的23名学生中,高于平均身高的人数为p1,在乙班的23名学生中,高于平均身高的人数为p2,则p1 p2(填“>”“<”或“=”);
(3)若每班只能有20人参加入场式队列表演,首先要求这20人与原来23人的身高平均数相同,其次要求这20人身高的方差尽可能小,则甲班未入选的3名学生的身高分别为 cm.
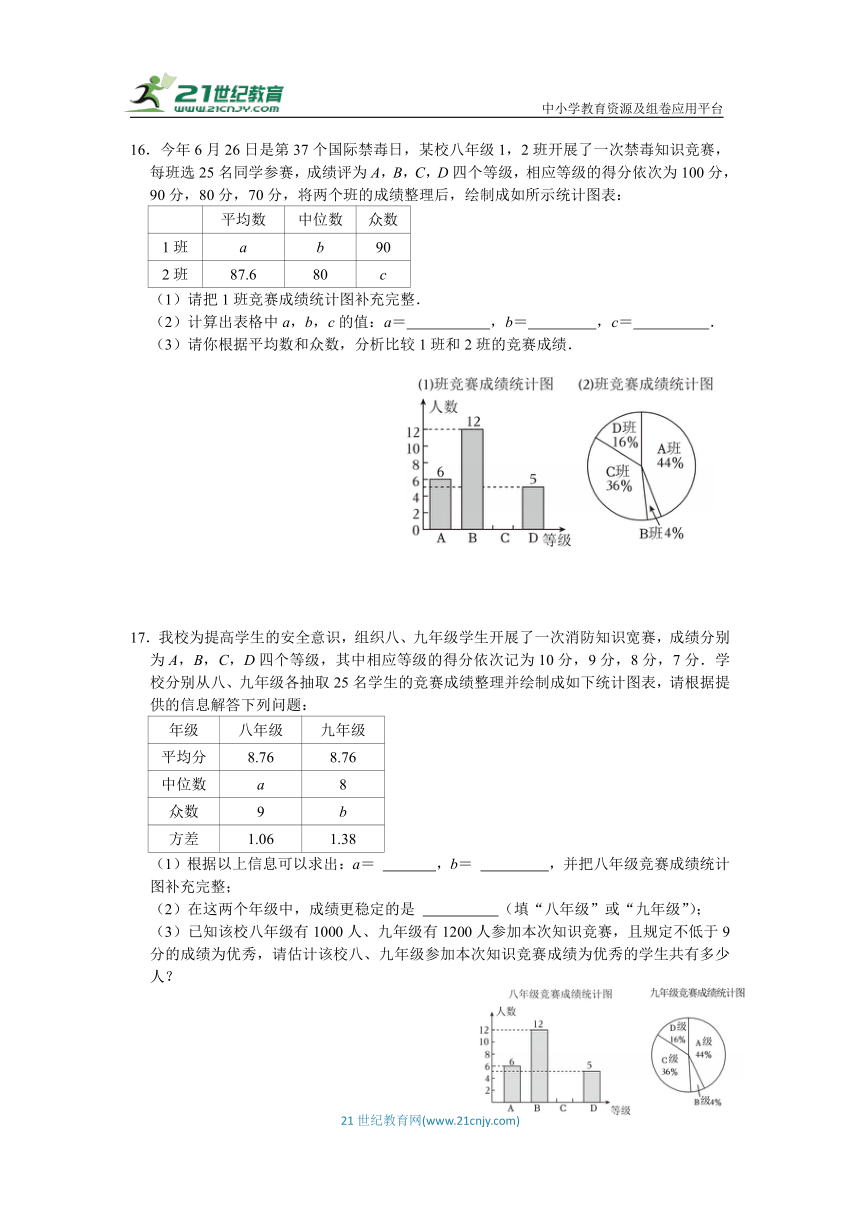
16.今年6月26日是第37个国际禁毒日,某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
17.我校为提高学生的安全意识,组织八、九年级学生开展了一次消防知识宽赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分,8分,7分.学校分别从八、九年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:
年级 八年级 九年级
平均分 8.76 8.76
中位数 a 8
众数 9 b
方差 1.06 1.38
(1)根据以上信息可以求出:a= ,b= ,并把八年级竞赛成绩统计图补充完整;
(2)在这两个年级中,成绩更稳定的是 (填“八年级”或“九年级”);
(3)已知该校八年级有1000人、九年级有1200人参加本次知识竞赛,且规定不低于9分的成绩为优秀,请估计该校八、九年级参加本次知识竞赛成绩为优秀的学生共有多少人?
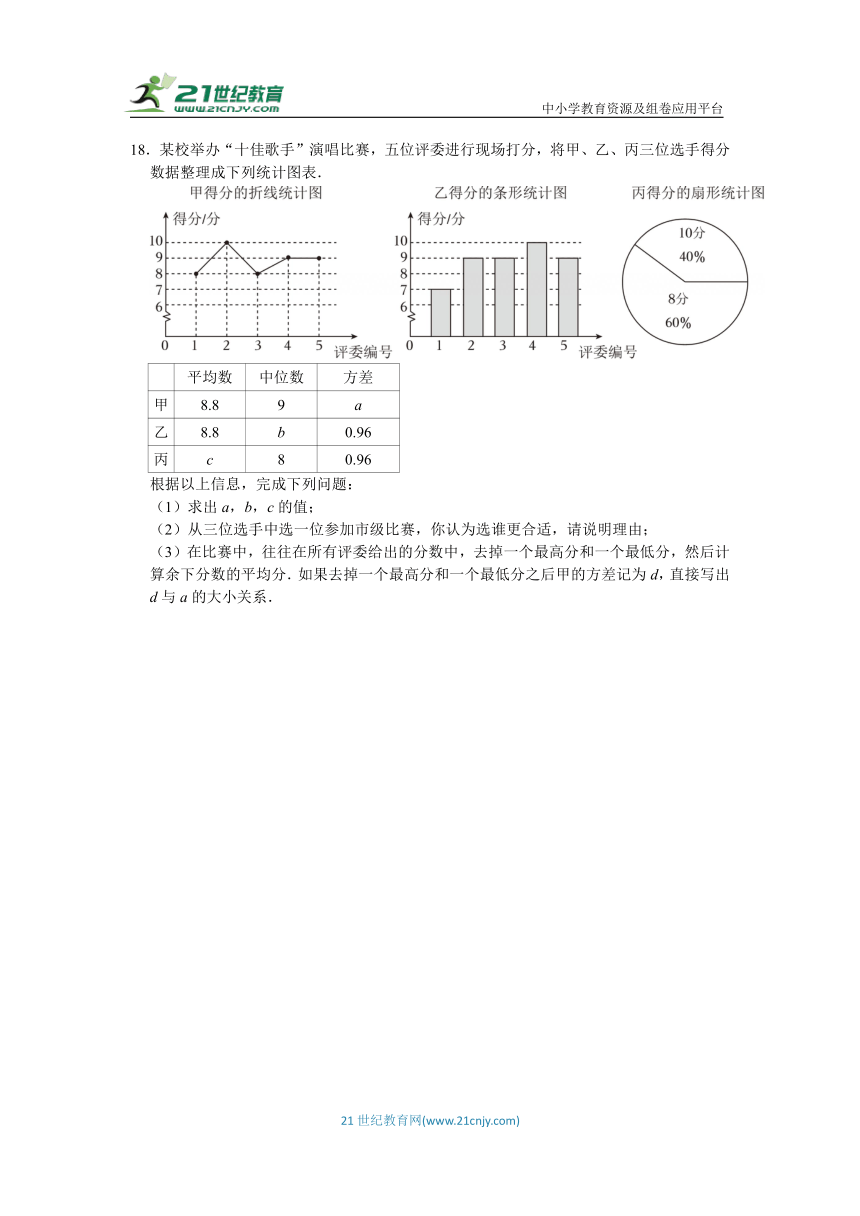
18.某校举办“十佳歌手”演唱比赛,五位评委进行现场打分,将甲、乙、丙三位选手得分数据整理成下列统计图表.
平均数 中位数 方差
甲 8.8 9 a
乙 8.8 b 0.96
丙 c 8 0.96
根据以上信息,完成下列问题:
(1)求出a,b,c的值;
(2)从三位选手中选一位参加市级比赛,你认为选谁更合适,请说明理由;
(3)在比赛中,往往在所有评委给出的分数中,去掉一个最高分和一个最低分,然后计算余下分数的平均分.如果去掉一个最高分和一个最低分之后甲的方差记为d,直接写出d与a的大小关系.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D C B C A A C D
1.【解答】解:∵甲、乙、丙、丁四位学生的平均成绩相同,且S甲2=2.1,S乙2=3.5,S丙2=5.6,S丁2=0.9,
∴丁的方差最小,
∴四人中这5次训练成绩最稳定的是丁,
故选:D.
2.【解答】解:将这组数据由小到大排列为:35,38,40,42,42,43.
(40+42)÷2=41.
众数为42,中位数为41.
故选:C.
3.【解答】解:换人前:中位数为:190,众数为:190,
平均数为:188.4,
换人后:中位数为:190,众数为:190,
平均数为:188.8,
∵用两名身高分别为186cm和190cm的队员换下场上两名身高是182cm和192cm的队员,数据波动变小,
∴方差变小,
综上所述,中位数不变,众数不变,方差变小,平均数变大,方差变小,
故选:B.
4.【解答】解:根据题意得:该组数据为11,9,8,6,6,共5个数,平均数为8,故A、B不符合题意;
添加一个数8后方差为:[(11﹣8)2+(9﹣8)2+2×(8﹣8)2+2×(6﹣8)2],
即添加一个数8后方差改变,故C选项符合题意;
这组数据,6出现的次数最多,
即这组数据的众数是6,故D选项不符合题意;
故选:C.
5.【解答】解:原数据平均数为:,
2,4,6,8,10中去掉一个最大数和一个最小数后数据为4,6,8,则新数据平均数为,
∴平均数不变,
原数据方差为:,
新数据方差为:,
∴平均数不变,方差变小,
故选:A.
6.【解答】解:去掉一个最高分和一个最低分对中位数没有影响,
故选:A.
7.【解答】解:小明的最终成绩为:85×80%+90×20%=68+18=86(分).
故选:C.
8.【解答】解:由条件可知x1+x2+x3+x4+x5=2×5=10,
=2,
∴,
∴另一组的平均数为:,
另一组数据的方差为:18,
故选:D.
二、填空题
9.【解答】解:根据题意可知,90×30%+80×30%+85×40%=27+24+34=85(分),
∴张少能的综合成绩为85分.
故答案为:85分.
10.【解答】解:由题意可知这组数据为5、3、6、4,
∴平均数为:(5+3+4+6)÷4=4.5.
故答案为:4.5.
11.【解答】解:∵两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别为5和﹣2,
∴x1+x2+……+xn=5n,y1+y2+……+yn=﹣2n,
∴x1+2y1,x2+2y2,…,xn+2yn的平均数为:(x1+2y1+x2+2y2+…+xn+2yn)
[(x1+x2+…+xn)+2(y1+y2+…+yn)]
[5n+2×(﹣2n)]
(5n﹣4n)
n
=1.
故答案为:1.
12.【解答】解:∵共有2+8+7+10+3=30个数据,
∴其中位数是第15、16个数据的平均数,而第15、16个数据均为1.3万步,
则中位数是1.3万步,
故答案为:1.3.
三、解答题
13.【解答】解:(1)该班平均每人三分钟定点投篮投中[0×10+8×6+10×10﹣11×5﹣6×12]÷48+25=25.4375个;
(2)该班定点投篮总共获得[8×6+10×10]×2﹣[11×5﹣+6×12]×1=169分.
14.【解答】解:(1)由扇形统计图可得,成绩为8分人数为10×50%=5 (人),
成绩为9分的人数为10×20%=2(人),
成绩为10分的人数为10×20%=2(人),
则成绩为7分的学生数为10﹣5﹣2﹣2=1(人)
∵出现次数最多的为8分,
∴七年级活动成绩的众数为8分
故答案为:1;8.
(2)将八年级的活动成绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数,
∵八年级10名学生活动成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分,
∵成绩为6分和7分的人数为1+2=3(人),
∴成绩为8分的人数为5﹣3=2(人),
成绩为9分的人数为10﹣5﹣2=3(人)
即a=2,b=3,
故答案为:2;3;
(3)不是,理由如下:
结合(1)(2)中所求可得七年级的优秀率为,
八年级的优秀率,
七年级的平均成绩为(分)
八年级的平均成绩为(分)
∵40%<50%,8.5>8.3,
∴本次活动中优秀率高的年级并不是平均成绩也高.
15.【解答】解:(1)把甲班23名学生的身高从小到大排列,排在中间的数是168,
故中位数m=168;
甲班23名学生的身高中166出现的次数最多,
故众数n=166;
(2)由题意得,p1=9,p2=12,
∴p1<p2.
故答案为:<;
(3)∵(163+164+180)=169,
∴甲班未入选的3名学生的身高分别为163、164、180cm.
故答案为:163、164、180.
16.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
17.【解答】解:(1)由条件可知:八年级中位数为从小到大排序后的第13名同学的成绩,
由条形统计图可知;从小到大排序后的第13名同学的成绩在等级B中,
故八年级中位数a=9,
由扇形图可知:44%>36%>16%>4%即等级A所占比例最多,
∴九年级众数b=10,
由题可知:八年级等级C人数为:25﹣6﹣12﹣5=2(人),
补全条形统计图如下:
故答案为:9,10;
(2)∵八、九年级平均分相同,而八年级中位数大于九年级中位数,八年级方差小于九年级方差,
∴八年级成绩更好,更稳定;
故答案为:八年级;
(3)八年级优秀人数为人.
九年级优秀人数为1200×(44%+4%)=576人.
∴两个年级优秀学生总人数为720+576=1296人.
18.【解答】解:(1)由甲得分的折线统计图可知,甲得分的排序为:10、9、9、8、8,
∴甲得分的方差a0.4,
由乙得分的条形统计图可知,乙得分的排序为:10、9、9、9、7,
∴乙得分的中位数b=9;
由扇形统计图可知,甲的平均数c=10×40%+8×60%=8.8,
故c
(2)选甲更合适.理由如下:
因为甲、乙、丙三人平均成绩一样,说明三人实力相当,但是甲的方差最小,说明甲的成绩更稳定,所以选甲;
(3)去掉一个最高分和一个最低分之后,甲的平均数为,
甲的方差d0.22,
∴0.22<0.56,即c
21世纪教育网(www.21cnjy.com)
第三章数据分析初步(A卷)单元测试浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.甲、乙、丙、丁四位学生参加立定跳远训练,他们近期5次训练的平均成绩相同,设甲、乙、丙、丁这5次训练成绩的方差分别是S甲2,S乙2,S丙2,S丁2,且S甲2=2.1,S乙2=3.5,S丙2=5.6,S丁2=0.9,则四位学生中这5次训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.为贯彻落实教育部《关于全面加强新时代大中小学劳动教育的意见》精神,把劳动教育纳入人才培养全过程,某校组织学生周末赴劳动教育实践基地开展锄地、除草、浇水、剪枝、捉鱼、采摘六项实践活动,已知六个项目参与人数(单位:人)分别是:35,38,40,42,42,43.则这组数据的众数和中位数分别是( )
A.38,39 B.42,40 C.42,41 D.42,42
3.某校篮球队5名场上队员的身高是182,188,190,190,192(单位:cm),现用两名身高分别为186cm和190cm的队员换下场上两名身高是182cm和192cm的队员,下列关于换人前后场上队员的身高说法正确的为( )
A.中位数变大,众数不变 B.中位数不变,方差变小
C.平均数变大,众数变小 D.平均数变小,方差变大
4.老师在黑板上写出一个计算方差的算式:,根据上式还原得到的数据,下列结论不正确的是( )
A.n=5 B.平均数为8
C.添加一个数8后方差不变 D.这组数据的众数是6
5.若从一组数据2,4,6,8,10中去掉一个最大数和一个最小数,则所得新数据与原数据相比( )
A.平均数不变,方差变小 B.平均数不变,方差变大
C.平均数变小,方差变小 D.平均数变小,方差变大
6.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.中位数 B.众数 C.平均数 D.方差
7.某校竞选学生会主席分为现场演讲和答辩两个环节,其中现场演讲分占80%,答辩分占20%,小明参加并在这两个环节中分别取得85分和90分的成绩,则小明的最终成绩为( )
A.80分 B.84分 C.86分 D.88分
8.如果一组数据x1,x2,…x5的平均数是2,方差是2,则另一组数据3x1﹣2,3x2﹣2,3x3﹣2,…3x5﹣2的平均数和方差分别是( )
A.2,2 B.2,6 C.4,4 D.4,18
二.填空题(每小题5分,满分20分)
9.学校举行篮球技能大赛,评委从控球技能、投球技能、身体素质三方面为选手打分,各项成绩均按百分制计,然后再按控球技能占30%、投球技能占30%、身体素质占40%计算选手的综合成绩(百分制).选手张少能控球技能得90分,投球技能得80分,身体素质得85分,则张少能的综合成绩为 .
10.一组数据的方差计算为:,则这组数据的平均数为 .
11.已知两组数据x1,x2,……,xn和y1,y2,……,yn的平均数分别为5和﹣2,则x1+2y1,x2+2y2,……,xn+2yn的平均数为 .
12.小明同学用手机软件记录了5月份每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,中位数是 万步.
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.求实中学积极落实“双减”政策,扎实有效地开展了多项体育运动.本学期七年级学生在体育老师的组织下开展了一次定点投篮比赛,如下表为七年级某班48人参加定点投篮比赛的情况记录,若标准数量为每人三分钟定点投篮投中25个.
定点投篮投中个数与标准数量的差值 ﹣11 ﹣6 0 8 10
人数 5 12 10 6 10
(1)该班平均每人三分钟定点投篮投中多少个?
(2)规定定点投篮投中个数达到标准数量记0分,超过标准数量,每多投1个加2分,每少投1个扣1分,求该班定点投篮总共获得多少分?
14.某校七、八年级开展了一次综合实践知识竞赛,按10分制进行评分,成绩(单位:分)均为不低于6的整数.为了解这次活动的效果,现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理,并绘制成统计图表,部分信息如下:
八年级10名学生活动成绩统计表
成绩(分) 6 7 8 9 10
人数 1 2 a b 2
已知八年级10名学生成绩的中位数为8.5分.
请根据以上信息,解答下列问题:
(1)样本中,七年级活动成绩为7分的学生数是 ,七年级活动成绩的众数为 分.
(2)a= ,b= .
(3)若认定活动成绩不低于9分为“优秀”,则根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
15.某校甲、乙两个班级各有23名学生进行校运动会入场式的队列训练,为了解这两个班级参加队列训练的学生的身高情况,测量并获取了这些学生的身高(单位:cm),数据整理如下:
a.甲班23名学生的身高:
163,163,164,165,165,166,166,166,166,167,167,168,169,169,170,171,171,172,173,173,174,179,180.
b.两班学生身高的平均数、中位数、众数如表所示:
班级 平均数 中位数 众数
甲 169 m n
乙 169 170 167
(1)写出表中m,n的值;
(2)在甲班的23名学生中,高于平均身高的人数为p1,在乙班的23名学生中,高于平均身高的人数为p2,则p1 p2(填“>”“<”或“=”);
(3)若每班只能有20人参加入场式队列表演,首先要求这20人与原来23人的身高平均数相同,其次要求这20人身高的方差尽可能小,则甲班未入选的3名学生的身高分别为 cm.
16.今年6月26日是第37个国际禁毒日,某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
17.我校为提高学生的安全意识,组织八、九年级学生开展了一次消防知识宽赛,成绩分别为A,B,C,D四个等级,其中相应等级的得分依次记为10分,9分,8分,7分.学校分别从八、九年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:
年级 八年级 九年级
平均分 8.76 8.76
中位数 a 8
众数 9 b
方差 1.06 1.38
(1)根据以上信息可以求出:a= ,b= ,并把八年级竞赛成绩统计图补充完整;
(2)在这两个年级中,成绩更稳定的是 (填“八年级”或“九年级”);
(3)已知该校八年级有1000人、九年级有1200人参加本次知识竞赛,且规定不低于9分的成绩为优秀,请估计该校八、九年级参加本次知识竞赛成绩为优秀的学生共有多少人?
18.某校举办“十佳歌手”演唱比赛,五位评委进行现场打分,将甲、乙、丙三位选手得分数据整理成下列统计图表.
平均数 中位数 方差
甲 8.8 9 a
乙 8.8 b 0.96
丙 c 8 0.96
根据以上信息,完成下列问题:
(1)求出a,b,c的值;
(2)从三位选手中选一位参加市级比赛,你认为选谁更合适,请说明理由;
(3)在比赛中,往往在所有评委给出的分数中,去掉一个最高分和一个最低分,然后计算余下分数的平均分.如果去掉一个最高分和一个最低分之后甲的方差记为d,直接写出d与a的大小关系.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D C B C A A C D
1.【解答】解:∵甲、乙、丙、丁四位学生的平均成绩相同,且S甲2=2.1,S乙2=3.5,S丙2=5.6,S丁2=0.9,
∴丁的方差最小,
∴四人中这5次训练成绩最稳定的是丁,
故选:D.
2.【解答】解:将这组数据由小到大排列为:35,38,40,42,42,43.
(40+42)÷2=41.
众数为42,中位数为41.
故选:C.
3.【解答】解:换人前:中位数为:190,众数为:190,
平均数为:188.4,
换人后:中位数为:190,众数为:190,
平均数为:188.8,
∵用两名身高分别为186cm和190cm的队员换下场上两名身高是182cm和192cm的队员,数据波动变小,
∴方差变小,
综上所述,中位数不变,众数不变,方差变小,平均数变大,方差变小,
故选:B.
4.【解答】解:根据题意得:该组数据为11,9,8,6,6,共5个数,平均数为8,故A、B不符合题意;
添加一个数8后方差为:[(11﹣8)2+(9﹣8)2+2×(8﹣8)2+2×(6﹣8)2],
即添加一个数8后方差改变,故C选项符合题意;
这组数据,6出现的次数最多,
即这组数据的众数是6,故D选项不符合题意;
故选:C.
5.【解答】解:原数据平均数为:,
2,4,6,8,10中去掉一个最大数和一个最小数后数据为4,6,8,则新数据平均数为,
∴平均数不变,
原数据方差为:,
新数据方差为:,
∴平均数不变,方差变小,
故选:A.
6.【解答】解:去掉一个最高分和一个最低分对中位数没有影响,
故选:A.
7.【解答】解:小明的最终成绩为:85×80%+90×20%=68+18=86(分).
故选:C.
8.【解答】解:由条件可知x1+x2+x3+x4+x5=2×5=10,
=2,
∴,
∴另一组的平均数为:,
另一组数据的方差为:18,
故选:D.
二、填空题
9.【解答】解:根据题意可知,90×30%+80×30%+85×40%=27+24+34=85(分),
∴张少能的综合成绩为85分.
故答案为:85分.
10.【解答】解:由题意可知这组数据为5、3、6、4,
∴平均数为:(5+3+4+6)÷4=4.5.
故答案为:4.5.
11.【解答】解:∵两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别为5和﹣2,
∴x1+x2+……+xn=5n,y1+y2+……+yn=﹣2n,
∴x1+2y1,x2+2y2,…,xn+2yn的平均数为:(x1+2y1+x2+2y2+…+xn+2yn)
[(x1+x2+…+xn)+2(y1+y2+…+yn)]
[5n+2×(﹣2n)]
(5n﹣4n)
n
=1.
故答案为:1.
12.【解答】解:∵共有2+8+7+10+3=30个数据,
∴其中位数是第15、16个数据的平均数,而第15、16个数据均为1.3万步,
则中位数是1.3万步,
故答案为:1.3.
三、解答题
13.【解答】解:(1)该班平均每人三分钟定点投篮投中[0×10+8×6+10×10﹣11×5﹣6×12]÷48+25=25.4375个;
(2)该班定点投篮总共获得[8×6+10×10]×2﹣[11×5﹣+6×12]×1=169分.
14.【解答】解:(1)由扇形统计图可得,成绩为8分人数为10×50%=5 (人),
成绩为9分的人数为10×20%=2(人),
成绩为10分的人数为10×20%=2(人),
则成绩为7分的学生数为10﹣5﹣2﹣2=1(人)
∵出现次数最多的为8分,
∴七年级活动成绩的众数为8分
故答案为:1;8.
(2)将八年级的活动成绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数,
∵八年级10名学生活动成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分,
∵成绩为6分和7分的人数为1+2=3(人),
∴成绩为8分的人数为5﹣3=2(人),
成绩为9分的人数为10﹣5﹣2=3(人)
即a=2,b=3,
故答案为:2;3;
(3)不是,理由如下:
结合(1)(2)中所求可得七年级的优秀率为,
八年级的优秀率,
七年级的平均成绩为(分)
八年级的平均成绩为(分)
∵40%<50%,8.5>8.3,
∴本次活动中优秀率高的年级并不是平均成绩也高.
15.【解答】解:(1)把甲班23名学生的身高从小到大排列,排在中间的数是168,
故中位数m=168;
甲班23名学生的身高中166出现的次数最多,
故众数n=166;
(2)由题意得,p1=9,p2=12,
∴p1<p2.
故答案为:<;
(3)∵(163+164+180)=169,
∴甲班未入选的3名学生的身高分别为163、164、180cm.
故答案为:163、164、180.
16.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
17.【解答】解:(1)由条件可知:八年级中位数为从小到大排序后的第13名同学的成绩,
由条形统计图可知;从小到大排序后的第13名同学的成绩在等级B中,
故八年级中位数a=9,
由扇形图可知:44%>36%>16%>4%即等级A所占比例最多,
∴九年级众数b=10,
由题可知:八年级等级C人数为:25﹣6﹣12﹣5=2(人),
补全条形统计图如下:
故答案为:9,10;
(2)∵八、九年级平均分相同,而八年级中位数大于九年级中位数,八年级方差小于九年级方差,
∴八年级成绩更好,更稳定;
故答案为:八年级;
(3)八年级优秀人数为人.
九年级优秀人数为1200×(44%+4%)=576人.
∴两个年级优秀学生总人数为720+576=1296人.
18.【解答】解:(1)由甲得分的折线统计图可知,甲得分的排序为:10、9、9、8、8,
∴甲得分的方差a0.4,
由乙得分的条形统计图可知,乙得分的排序为:10、9、9、9、7,
∴乙得分的中位数b=9;
由扇形统计图可知,甲的平均数c=10×40%+8×60%=8.8,
故c
(2)选甲更合适.理由如下:
因为甲、乙、丙三人平均成绩一样,说明三人实力相当,但是甲的方差最小,说明甲的成绩更稳定,所以选甲;
(3)去掉一个最高分和一个最低分之后,甲的平均数为,
甲的方差d0.22,
∴0.22<0.56,即c
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
