3.1直线与圆的位置关系(2)
图片预览

文档简介
课题:3.1直线与圆的位置关系(2)之一
学习目标:
1、通过动手操作,经历圆的切线的判定定理得产生过程,并帮助理解与记忆;
2、在探索圆的切线的判定定理的过程中,体验切线的判定、切线的特殊性;
3、通过圆的切线的判定定理得学习,培养学生学习主动性和积极性。
学习重点:圆的切线的判定定理
学习难点:定理的运用中,辅助线的添加方法。
学习过程:
一、预习检查和复习
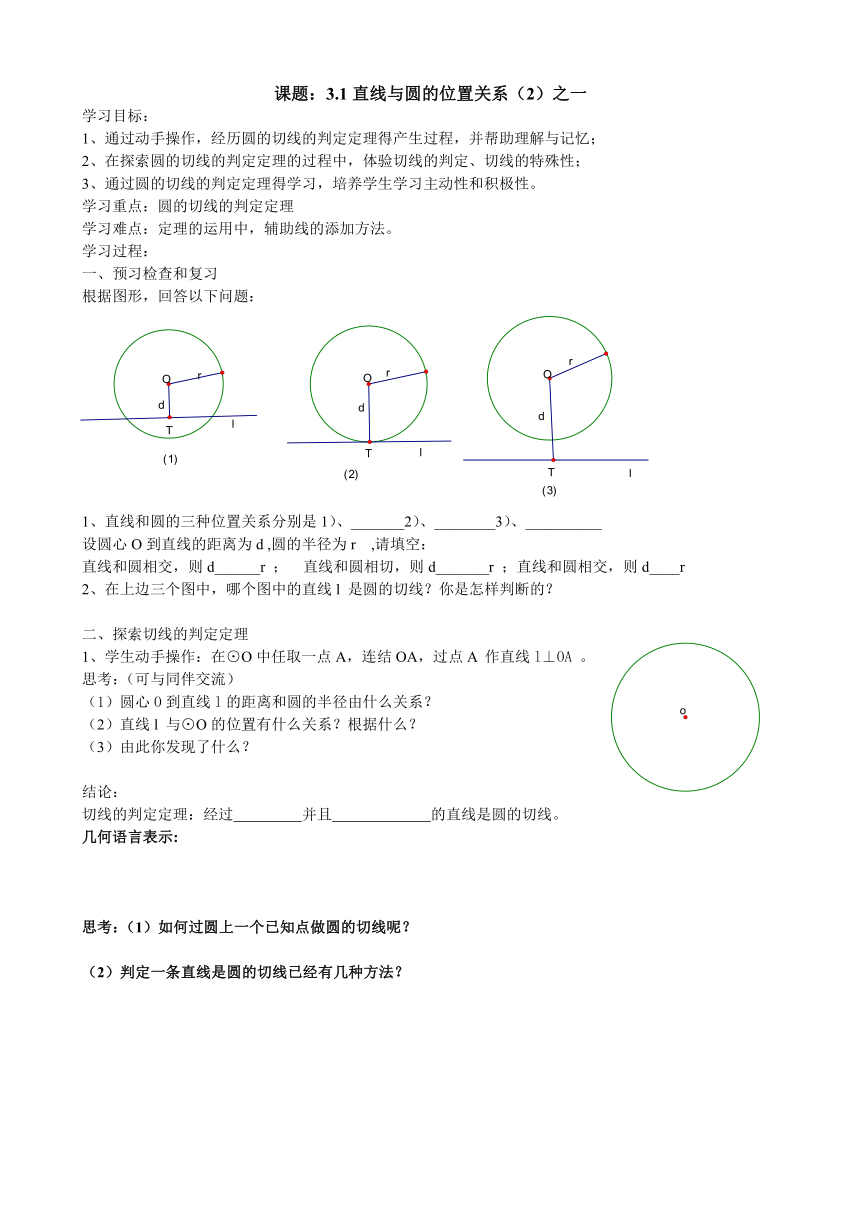
根据图形,回答以下问题:
1、直线和圆的三种位置关系分别是1)、_______2)、________3)、__________
设圆心O到直线的距离为d ,圆的半径为r ,请填空:
直线和圆相交,则d______r ; 直线和圆相切,则d_______r ;直线和圆相交,则d____r
2、在上边三个图中,哪个图中的直线l 是圆的切线?你是怎样判断的?
二、探索切线的判定定理
1、学生动手操作:在⊙O中任取一点A,连结OA,过点A 作直线l⊥OA 。
思考:(可与同伴交流)
(1)圆心O到直线l的距离和圆的半径由什么关系?
(2)直线l 与⊙O的位置有什么关系?根据什么?
(3)由此你发现了什么?
结论:
切线的判定定理:经过 并且 的直线是圆的切线。
几何语言表示:
思考:(1)如何过圆上一个已知点做圆的切线呢?
(2)判定一条直线是圆的切线已经有几种方法?
2、做一做(1)下列哪个图形的直线l 与⊙O相切?( )
小结:证明一条直线为圆的切线时,必须两个条件缺一不可:①
②
(2)课本第52页课内练习第1题
(3)课本第51页做一做
三、应用定理,强化训练
例1、已知:如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
例2、如图,已知OA=OB=5厘米,AB=8厘米,⊙O的直径为6厘米。
求证:AB与⊙O相切。
思考:以上两例辅助线的添加法是否相同?有什么规律吗?
规律:
(1)若直线与圆有公共点时,辅助线的作法是“连结圆心和公共点”,再证明直线和半径垂直。
(2)当直线与圆并没有明确有公共点时,辅助线的作法是“过圆心向直线作垂线”再证明圆心到直线的距离等于圆的半径。
巩固练习
练习1:判断下列命题是否正确
(1)经过半径的外端的直线是圆的切线
(2)垂直于半径的直线是圆的切线;
(3)过直径的外端并且垂直于这条直径的直线是圆的切线;
(4)和圆有一个公共点的直线是圆的切线;
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切。
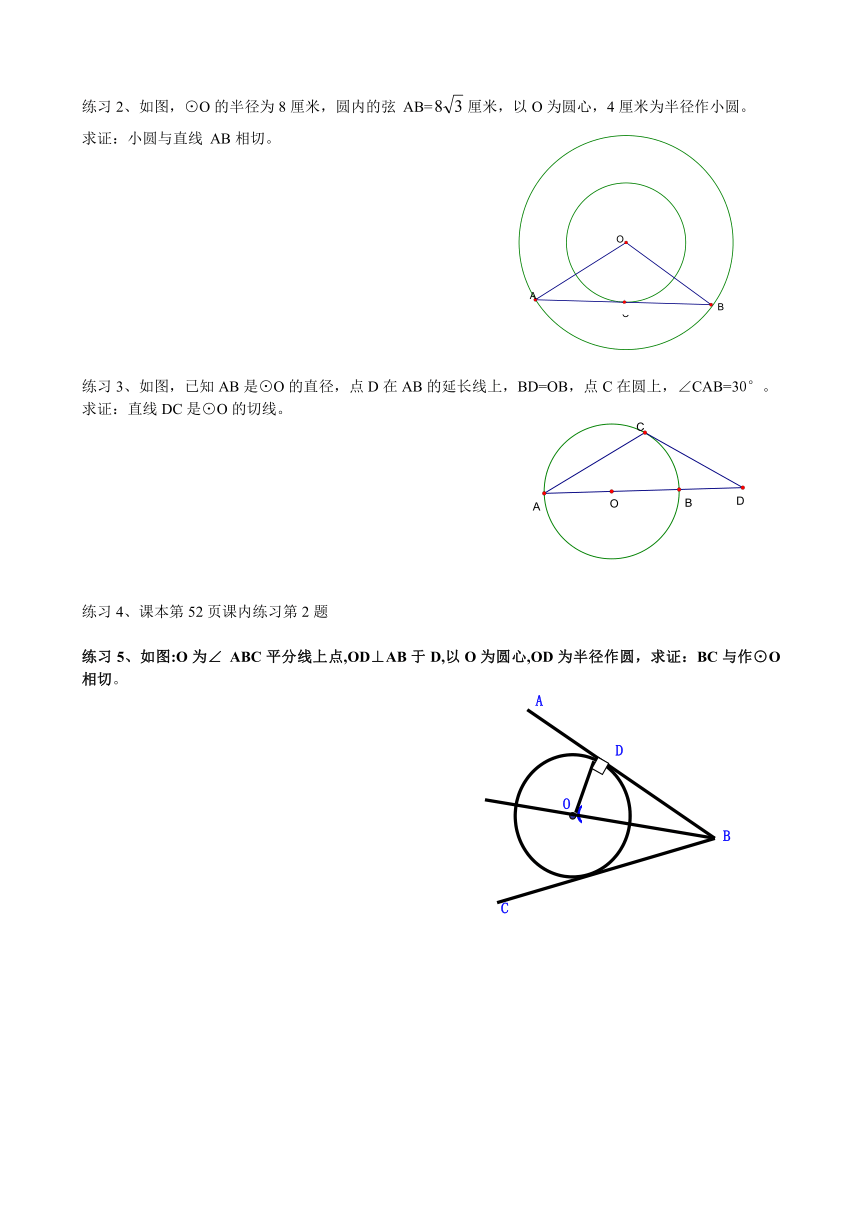
练习2、如图,⊙O的半径为8厘米,圆内的弦 AB=厘米,以O为圆心,4厘米为半径作小圆。
求证:小圆与直线 AB相切。
练习3、如图,已知AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°。
求证:直线DC是⊙O的切线。
练习4、课本第52页课内练习第2题
练习5、如图:O为∠ ABC平分线上点,OD⊥AB于D,以O为圆心,OD为半径作圆,求证:BC与作⊙O相切。
课外拓展:
1.如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G,⊙O是△CGF的外接圆
求证:CE是⊙O的切线。
2、如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC.
(1)求证:DE是⊙O的切线.
(2)若∠C=30°,CD=10cm,求⊙O的半径.
四、小结提高:
1、切线的判定定理:经过 并且垂直于 的直线是圆的切线。
2、到目前为止,判定一条直线是圆的切线有三种方法,分别是:
(1)根据切线的定义判定:即与圆有 公共点的直线是圆的切线。
(2)根据圆心到直线的距离来判定:即与圆心的距离等于 的直线是圆的切线。
(3)根据切线的判定定理来判定:即经过半径的 并且 这条半径的直线是圆的切线。
3、证明一条直线是圆的切线常用的辅助线有两种:
(1)如果已知直线过圆上某一点,则作 ,后证明 。
(2)如果直线与圆的公共点没有明确,则 ,后证明 。
五、作业布置:见作业本和书上练习。
预习例3
教学案 3.1直线与圆的位置关系(2)之二
学习目标:
1、进一步掌握切线的判定定理,并能初步运用它解决问题;
2、通过例题教学,培养和提高学生分析问题解决问题的能力。
学习重点与难点:综合运用切线的判定定理。
学习关键:掌握切线的判定方法两种方法的理解是学好本节课的应用。
学习过程:
一、知识回顾和预习检查
判定直线与圆相切,常用的方法有哪些?
1、 ; 2、 ;3、 。
二、基础热身
1、在Rt△ABC中,∠C=Rt∠,AC=BC,以AB上的高CD为直径作一个圆,与这个圆相切的直线有( )
A、AC B、AC、BC C、AB D、AC、BC、AB
2、如图,点 A在⊙O上,由下列条件能判定直线AB和⊙O相切的有( )
①∠B=40°,∠O=50°,②sinB=1/2,③tanB×tanO=1,
④⊙O 过OB的中点,∠O=60°
A、① B、①② C、①②③ D、①③④
3、已知⊙O的直径为10厘米,如果圆心O到直线l 的距离为4.5厘米,那么直线l 与⊙O有 个公共点。
三、例题讲解
例1、(即课本的例2)已知如图,D是⊙O外一点,DO的延长线交⊙O于点A,点C在圆上,且AC=CD, ∠D=30°。
求证:直线CD是⊙O的切线。
做一做:如图AB是⊙O的直径,
(1)分别过A,B作⊙O的切线a,b.
(2) 直线a,b的位置关系;
(3)作出与直线a垂直的⊙O的切线
例2、如图,台风中心P(100,200)沿北偏东30°的方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540 )中,哪些受到这次台风的影响,哪些不受到这次台风的影响?
四、课内练习
1:如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于S点。
(1)过点P作⊙O的切线.
(2)过点P的切线交OT于Q,判断S是不是OQ的中点,并说明理由.
2、如图,AB是⊙O的直径,弦AD平分∠BAC,过A作AC⊥DC,
求证:DC是⊙O的切线。
3、如图,已知四边形ABCD是直角梯形,AD∥BC,AB⊥BC,CD=AD+BC。
求证:以CD为直径的⊙O与AB相切
4、如图,在Rt△ABC中,∠ACB=Rt∠,CD⊥AB于点D。
(1)求证:BC是△ADC的外接圆的切线;
(2) △BDC的外接圆的切线是哪一条?为什么?
(3)若AC=5,BC=12,以C为圆心作圆C,使圆C与 AB相切,则圆C的半径是多少?(p53 T6)
5、如图,AB是⊙O的直径,BC切⊙O于点B,连结OC,过A作AD∥OC,交⊙O于点D,连结DC。求证:CD是⊙O的切线。
6.请任意画一个圆,并在这个圆所在的平面内任意取一点P.
(1)过点P是否都能作这个圆的切线
(2)点P在什么位置时,能作并且只能作一条切线
(3)点P在什么位置时,能作两条切线 这两条切线有什么特性
(4)能作多于2条的切线吗
五.小结提高:
1.切线的判定定理:
2.用途:(1) (2)
3.方法:证明一条直线是圆的切线常用的辅助线有两种:
(1)如果已知直线过圆上某一点,则作 ,后证明 。
(2)如果直线与圆的公共点没有明确,则 ,后证明 。
四、布置作业:
1、已知,如图,A是半径为2的⊙O上一点,P是OA延长线上的动点,过P点作⊙O的切线为B.
(1)当PB=4时,求PO的值。
(2)⊙O上是否存在点C,使△ PBC为等边三角形?若存在,请求出此时PB的值,若不存在,请说明理由。
C
B
A
·O
C
B
A
·O
D
B
O
O
A
C
E
D
C
B
A
O
T
S
P
O
O
A
C
D
B
B
C
D
A
B
C
D
O
A
学习目标:
1、通过动手操作,经历圆的切线的判定定理得产生过程,并帮助理解与记忆;
2、在探索圆的切线的判定定理的过程中,体验切线的判定、切线的特殊性;
3、通过圆的切线的判定定理得学习,培养学生学习主动性和积极性。
学习重点:圆的切线的判定定理
学习难点:定理的运用中,辅助线的添加方法。
学习过程:
一、预习检查和复习
根据图形,回答以下问题:
1、直线和圆的三种位置关系分别是1)、_______2)、________3)、__________
设圆心O到直线的距离为d ,圆的半径为r ,请填空:
直线和圆相交,则d______r ; 直线和圆相切,则d_______r ;直线和圆相交,则d____r
2、在上边三个图中,哪个图中的直线l 是圆的切线?你是怎样判断的?
二、探索切线的判定定理
1、学生动手操作:在⊙O中任取一点A,连结OA,过点A 作直线l⊥OA 。
思考:(可与同伴交流)
(1)圆心O到直线l的距离和圆的半径由什么关系?
(2)直线l 与⊙O的位置有什么关系?根据什么?
(3)由此你发现了什么?
结论:
切线的判定定理:经过 并且 的直线是圆的切线。
几何语言表示:
思考:(1)如何过圆上一个已知点做圆的切线呢?
(2)判定一条直线是圆的切线已经有几种方法?
2、做一做(1)下列哪个图形的直线l 与⊙O相切?( )
小结:证明一条直线为圆的切线时,必须两个条件缺一不可:①
②
(2)课本第52页课内练习第1题
(3)课本第51页做一做
三、应用定理,强化训练
例1、已知:如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
例2、如图,已知OA=OB=5厘米,AB=8厘米,⊙O的直径为6厘米。
求证:AB与⊙O相切。
思考:以上两例辅助线的添加法是否相同?有什么规律吗?
规律:
(1)若直线与圆有公共点时,辅助线的作法是“连结圆心和公共点”,再证明直线和半径垂直。
(2)当直线与圆并没有明确有公共点时,辅助线的作法是“过圆心向直线作垂线”再证明圆心到直线的距离等于圆的半径。
巩固练习
练习1:判断下列命题是否正确
(1)经过半径的外端的直线是圆的切线
(2)垂直于半径的直线是圆的切线;
(3)过直径的外端并且垂直于这条直径的直线是圆的切线;
(4)和圆有一个公共点的直线是圆的切线;
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切。
练习2、如图,⊙O的半径为8厘米,圆内的弦 AB=厘米,以O为圆心,4厘米为半径作小圆。
求证:小圆与直线 AB相切。
练习3、如图,已知AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°。
求证:直线DC是⊙O的切线。
练习4、课本第52页课内练习第2题
练习5、如图:O为∠ ABC平分线上点,OD⊥AB于D,以O为圆心,OD为半径作圆,求证:BC与作⊙O相切。
课外拓展:
1.如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G,⊙O是△CGF的外接圆
求证:CE是⊙O的切线。
2、如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC.
(1)求证:DE是⊙O的切线.
(2)若∠C=30°,CD=10cm,求⊙O的半径.
四、小结提高:
1、切线的判定定理:经过 并且垂直于 的直线是圆的切线。
2、到目前为止,判定一条直线是圆的切线有三种方法,分别是:
(1)根据切线的定义判定:即与圆有 公共点的直线是圆的切线。
(2)根据圆心到直线的距离来判定:即与圆心的距离等于 的直线是圆的切线。
(3)根据切线的判定定理来判定:即经过半径的 并且 这条半径的直线是圆的切线。
3、证明一条直线是圆的切线常用的辅助线有两种:
(1)如果已知直线过圆上某一点,则作 ,后证明 。
(2)如果直线与圆的公共点没有明确,则 ,后证明 。
五、作业布置:见作业本和书上练习。
预习例3
教学案 3.1直线与圆的位置关系(2)之二
学习目标:
1、进一步掌握切线的判定定理,并能初步运用它解决问题;
2、通过例题教学,培养和提高学生分析问题解决问题的能力。
学习重点与难点:综合运用切线的判定定理。
学习关键:掌握切线的判定方法两种方法的理解是学好本节课的应用。
学习过程:
一、知识回顾和预习检查
判定直线与圆相切,常用的方法有哪些?
1、 ; 2、 ;3、 。
二、基础热身
1、在Rt△ABC中,∠C=Rt∠,AC=BC,以AB上的高CD为直径作一个圆,与这个圆相切的直线有( )
A、AC B、AC、BC C、AB D、AC、BC、AB
2、如图,点 A在⊙O上,由下列条件能判定直线AB和⊙O相切的有( )
①∠B=40°,∠O=50°,②sinB=1/2,③tanB×tanO=1,
④⊙O 过OB的中点,∠O=60°
A、① B、①② C、①②③ D、①③④
3、已知⊙O的直径为10厘米,如果圆心O到直线l 的距离为4.5厘米,那么直线l 与⊙O有 个公共点。
三、例题讲解
例1、(即课本的例2)已知如图,D是⊙O外一点,DO的延长线交⊙O于点A,点C在圆上,且AC=CD, ∠D=30°。
求证:直线CD是⊙O的切线。
做一做:如图AB是⊙O的直径,
(1)分别过A,B作⊙O的切线a,b.
(2) 直线a,b的位置关系;
(3)作出与直线a垂直的⊙O的切线
例2、如图,台风中心P(100,200)沿北偏东30°的方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540 )中,哪些受到这次台风的影响,哪些不受到这次台风的影响?
四、课内练习
1:如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于S点。
(1)过点P作⊙O的切线.
(2)过点P的切线交OT于Q,判断S是不是OQ的中点,并说明理由.
2、如图,AB是⊙O的直径,弦AD平分∠BAC,过A作AC⊥DC,
求证:DC是⊙O的切线。
3、如图,已知四边形ABCD是直角梯形,AD∥BC,AB⊥BC,CD=AD+BC。
求证:以CD为直径的⊙O与AB相切
4、如图,在Rt△ABC中,∠ACB=Rt∠,CD⊥AB于点D。
(1)求证:BC是△ADC的外接圆的切线;
(2) △BDC的外接圆的切线是哪一条?为什么?
(3)若AC=5,BC=12,以C为圆心作圆C,使圆C与 AB相切,则圆C的半径是多少?(p53 T6)
5、如图,AB是⊙O的直径,BC切⊙O于点B,连结OC,过A作AD∥OC,交⊙O于点D,连结DC。求证:CD是⊙O的切线。
6.请任意画一个圆,并在这个圆所在的平面内任意取一点P.
(1)过点P是否都能作这个圆的切线
(2)点P在什么位置时,能作并且只能作一条切线
(3)点P在什么位置时,能作两条切线 这两条切线有什么特性
(4)能作多于2条的切线吗
五.小结提高:
1.切线的判定定理:
2.用途:(1) (2)
3.方法:证明一条直线是圆的切线常用的辅助线有两种:
(1)如果已知直线过圆上某一点,则作 ,后证明 。
(2)如果直线与圆的公共点没有明确,则 ,后证明 。
四、布置作业:
1、已知,如图,A是半径为2的⊙O上一点,P是OA延长线上的动点,过P点作⊙O的切线为B.
(1)当PB=4时,求PO的值。
(2)⊙O上是否存在点C,使△ PBC为等边三角形?若存在,请求出此时PB的值,若不存在,请说明理由。
C
B
A
·O
C
B
A
·O
D
B
O
O
A
C
E
D
C
B
A
O
T
S
P
O
O
A
C
D
B
B
C
D
A
B
C
D
O
A
