相似三角形性质判定的应用
图片预览

文档简介
课件9张PPT。平湖市福臻中学
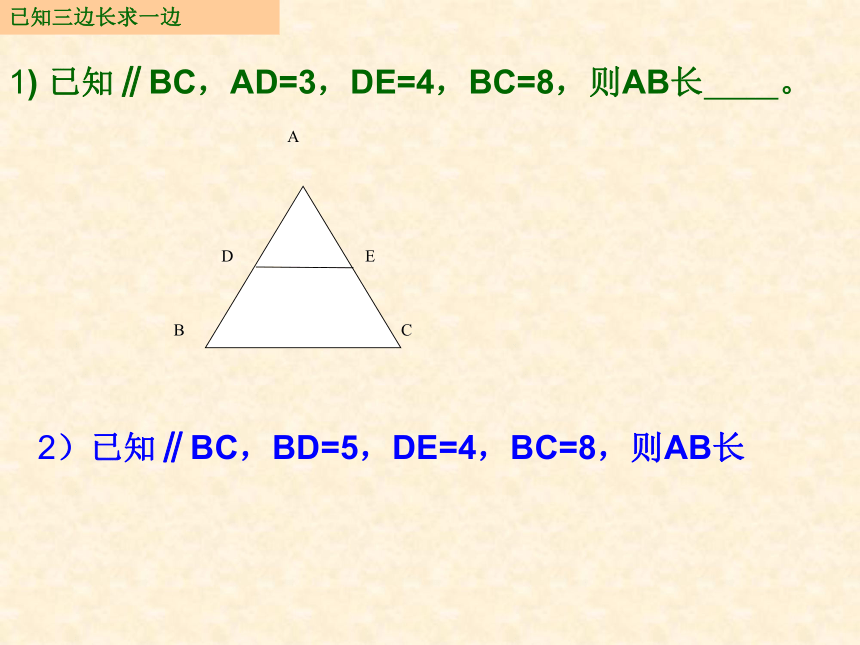
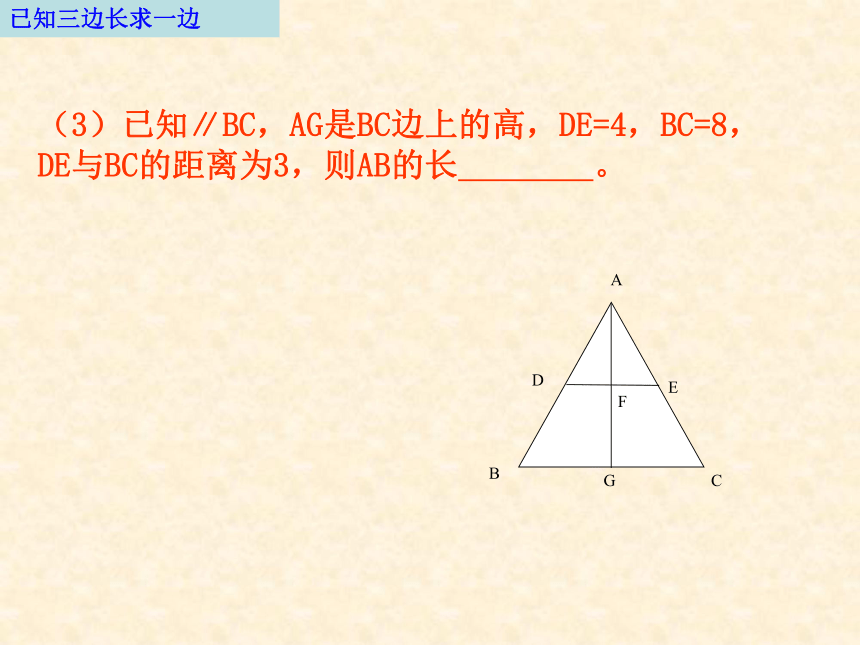
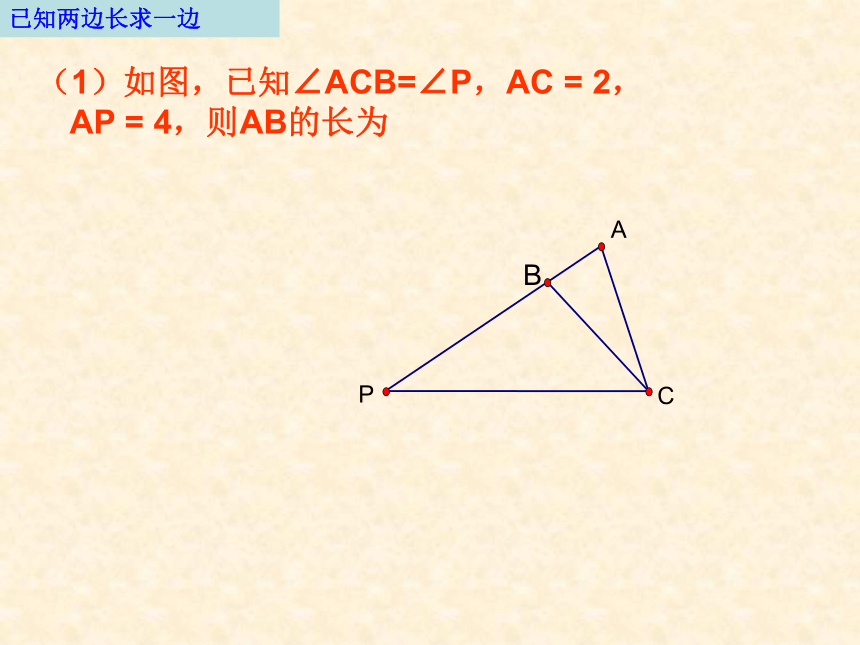
吴 燕4.1比例线段(三)相似三角形性质,判定的应用已知三边长求一边1) 已知∥BC,AD=3,DE=4,BC=8,则AB长 。2)已知∥BC,BD=5,DE=4,BC=8,则AB长 已知三边长求一边(3)已知∥BC,AG是BC边上的高,DE=4,BC=8,DE与BC的距离为3,则AB的长 。(1)如图,已知∠ACB=∠P,AC = 2,AP = 4,则AB的长为 已知两边长求一边(2)如图,矩形ABCD∽矩形CDFE,AB=2,
BC=4,则EC长 ,BE长 已知两边长求一边(1)如图,已知AB=AC=2,∠A=36°,BE平分∠ABC,则AE长为 已知两边长求一边(3)如图,已知矩形ABCD∽矩形CDFE,且BC=2,AB=BF,则CF= 已知两边长求一边二、利用相似三角形求二次函数及最值1.已知三角形ABC的边BC=8,高AD=16,矩形PQMN的四个顶点在三角形的边上,设QM为,矩形PQMN的面积为S,求:
(1)S关于的函数关系式及自变量的取值范围
(2)当自变量取何值时,矩形面积最大?最大为多少?2、如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒后,四边形ABQP的面积为S米2。
(1)求面积S与时间t的关系式;BADQCP
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。 二、利用相似三角形求二次函数及最值
吴 燕4.1比例线段(三)相似三角形性质,判定的应用已知三边长求一边1) 已知∥BC,AD=3,DE=4,BC=8,则AB长 。2)已知∥BC,BD=5,DE=4,BC=8,则AB长 已知三边长求一边(3)已知∥BC,AG是BC边上的高,DE=4,BC=8,DE与BC的距离为3,则AB的长 。(1)如图,已知∠ACB=∠P,AC = 2,AP = 4,则AB的长为 已知两边长求一边(2)如图,矩形ABCD∽矩形CDFE,AB=2,
BC=4,则EC长 ,BE长 已知两边长求一边(1)如图,已知AB=AC=2,∠A=36°,BE平分∠ABC,则AE长为 已知两边长求一边(3)如图,已知矩形ABCD∽矩形CDFE,且BC=2,AB=BF,则CF= 已知两边长求一边二、利用相似三角形求二次函数及最值1.已知三角形ABC的边BC=8,高AD=16,矩形PQMN的四个顶点在三角形的边上,设QM为,矩形PQMN的面积为S,求:
(1)S关于的函数关系式及自变量的取值范围
(2)当自变量取何值时,矩形面积最大?最大为多少?2、如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒后,四边形ABQP的面积为S米2。
(1)求面积S与时间t的关系式;BADQCP
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。 二、利用相似三角形求二次函数及最值
同课章节目录
