3.2(三角形的内切圆)(教学案)
图片预览

文档简介
班级: 姓名:
§3.2直线和圆的位置关系(3)
学习目标:
1.会过圆上一点画圆的切线; 2.会作三角形的内切圆;
3.理解三角形内切圆的有关概念.
学习重点:掌握会作三角形的内切圆的画法,理解三角形内切圆的有关概念.
学习难点:作三角形的内切圆.
学习过程:
【知识回顾】
1.在角平分线上的点到 的距离相等。
角的内部,到 的点,在这个角的平分线上。
2.圆的切线的判定与性质:
经过半径的 并且 的直线是圆的切线.
圆的切线 经过切点的 .
【问题情境】
从一块三角形的材料上截下一块圆形的用料,怎样才能使圆的面积尽可能最大呢?
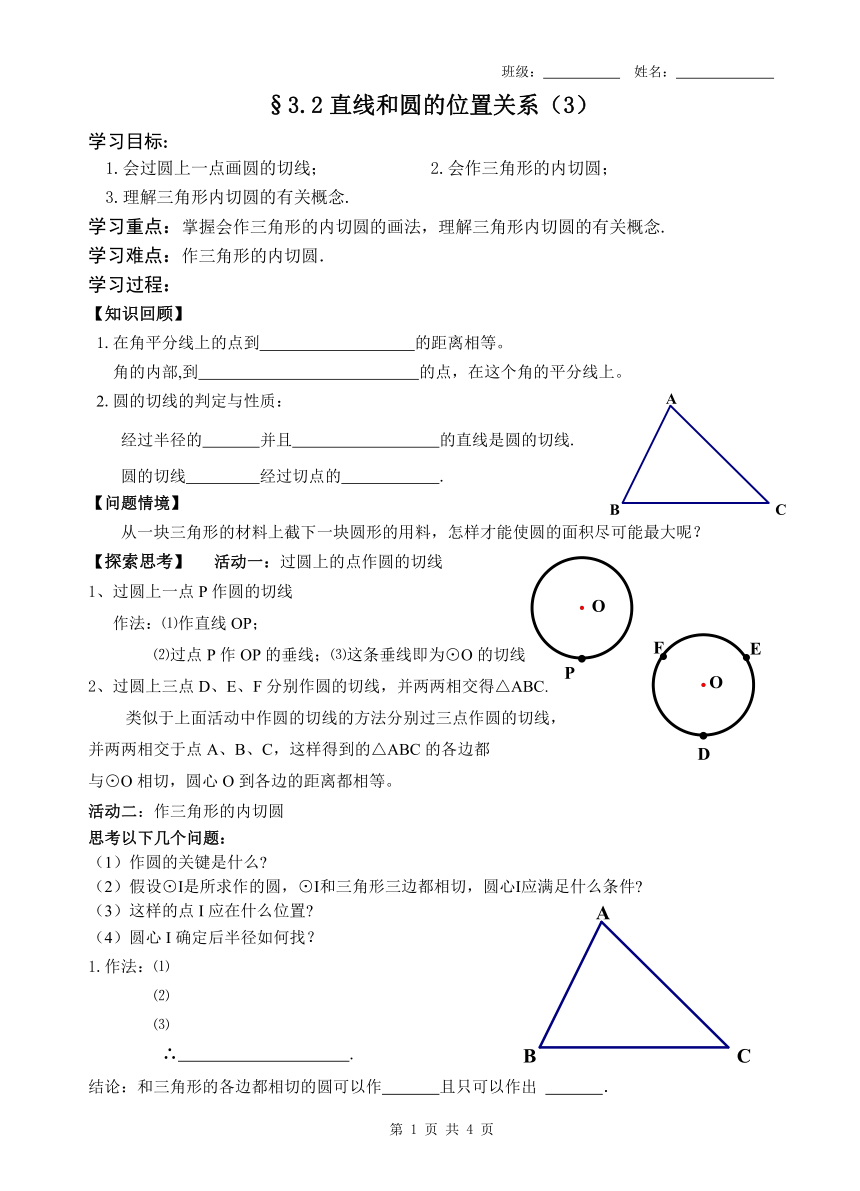
【探索思考】 活动一:过圆上的点作圆的切线
1、过圆上一点P作圆的切线
作法:⑴作直线OP;
⑵过点P作OP的垂线;⑶这条垂线即为⊙O的切线
2、过圆上三点D、E、F分别作圆的切线,并两两相交得△ABC.
类似于上面活动中作圆的切线的方法分别过三点作圆的切线,
并两两相交于点A、B、C,这样得到的△ABC的各边都
与⊙O相切,圆心O到各边的距离都相等。
活动二:作三角形的内切圆
思考以下几个问题:
(1)作圆的关键是什么
(2)假设⊙I是所求作的圆,⊙I和三角形三边都相切,圆心I应满足什么条件
(3)这样的点I应在什么位置
(4)圆心I确定后半径如何找?
1.作法:⑴
⑵
⑶
∴ .
结论:和三角形的各边都相切的圆可以作 且只可以作出 .
2.与三角形各边都相切的圆叫做 ,内切圆的圆心叫做 ,这个三角
形叫做圆的 。它是三角形 的交点,这个点到三角形
的距离相等.(注意:⑴一个三角形的内切圆是惟一的;⑵内心与外心的区别.)
三角形内心的性质: 三角形外心的性质:
【典型例题】
【练习2】如图,点O是△ABC的内心.根据以下条件,求∠BOC的度数.
(1)∠B=50°,∠C=60°; (2)∠A=50°.
解(1): 解(2):
【练习拓展】您能用一个代数式表示∠BOC与∠A之间的数量关系?
【练习3】如图:点I是△ABC的内心,AI交边BC于点D,交△ABC外接圆于点E,连接BE.
试说明:BE=IE.
【练习4】如图,在△ABC中,内切圆I与边BC、CA、AB分别相切于点D、E、F,∠B=60°,∠C=70°,求∠EDF的度数。
【练习5】如图:点I是△ABC的内心,AI交边BC于点D,交△ABC外接圆于点E,连接BE.
△BED和△AEB相似吗?请说明理由.
拓展提高
A
课堂小结:
①三角形的外心是三角形 的交点
①三角形的内心是三角形 线的交点
②三角形的外心到 的距离相等
②三角形的内心到 的距离相等
③三角形的外心 在三角形的
③三角形的内心一定在三角形的
例1、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱.圆柱的下底面是圆是
直三棱柱上底面等边三角形的内切圆.已知直三棱柱的底面等边三角形边长为3cm,
求圆柱底面的半径。
例2、如图,设△ABC的边BC=a,CA=b,AB=c,设a+b+c=l,n= l,内切圆O和各边分别相切
于D,E,F。求证:(1)AF+BC= l
(2)AD=AF=n-a,BE=BD=n-b,CF=CE=n-c。
例3、已知△ABC的三边BC,AB,AC分别为a,b,c,I为内心,内切圆半径为r,
求△ABC的面积S(用a,b,c,r表示)
例4、已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、AB的长分别为a、b、c,
求其内切圆O的半径长。
A
B
C
a
c
b
r
【练习1】
⑴边长为3,4,5的三角形的内切圆半径是__⑵边长为5,5,6的三角形的内切圆半径是__
如图,△ABC中,I是内心,∠BAC的平分线和△ABC的外接圆相交于点E,与BC交于点D.
求证:(1)IE=BE
设△ABC外接圆半径R=3,IE=2,AE=x,DE=y,当点A在优弧BC上运动时,
求函数y与自变量x间的函数关系式,并指出自变量的取值范围.
O
¤
I
C
B
D
1.本节课从实际问题入手,探索得出三角形内切圆的作法 .
2.通过类比三角形的外接圆与圆的内接三角形概念得出三角形的内切圆、圆的外切三角形概念,
并介绍了多边形的内切圆、圆的外切多边形的概念。
3.学习时要明确“接”和“切”的含义、弄清“内心”与“外心”的区别,
4.利用三角形内心的性质解题时,要注意整体思想的运用,在解决实际问题时,要注意把实际
问题转化为数学问题。
5.5-3 直线和圆的位置关系(三角形的内切圆) 第 4 页 共 4 页
第 5 页 共 4 页
§3.2直线和圆的位置关系(3)
学习目标:
1.会过圆上一点画圆的切线; 2.会作三角形的内切圆;
3.理解三角形内切圆的有关概念.
学习重点:掌握会作三角形的内切圆的画法,理解三角形内切圆的有关概念.
学习难点:作三角形的内切圆.
学习过程:
【知识回顾】
1.在角平分线上的点到 的距离相等。
角的内部,到 的点,在这个角的平分线上。
2.圆的切线的判定与性质:
经过半径的 并且 的直线是圆的切线.
圆的切线 经过切点的 .
【问题情境】
从一块三角形的材料上截下一块圆形的用料,怎样才能使圆的面积尽可能最大呢?
【探索思考】 活动一:过圆上的点作圆的切线
1、过圆上一点P作圆的切线
作法:⑴作直线OP;
⑵过点P作OP的垂线;⑶这条垂线即为⊙O的切线
2、过圆上三点D、E、F分别作圆的切线,并两两相交得△ABC.
类似于上面活动中作圆的切线的方法分别过三点作圆的切线,
并两两相交于点A、B、C,这样得到的△ABC的各边都
与⊙O相切,圆心O到各边的距离都相等。
活动二:作三角形的内切圆
思考以下几个问题:
(1)作圆的关键是什么
(2)假设⊙I是所求作的圆,⊙I和三角形三边都相切,圆心I应满足什么条件
(3)这样的点I应在什么位置
(4)圆心I确定后半径如何找?
1.作法:⑴
⑵
⑶
∴ .
结论:和三角形的各边都相切的圆可以作 且只可以作出 .
2.与三角形各边都相切的圆叫做 ,内切圆的圆心叫做 ,这个三角
形叫做圆的 。它是三角形 的交点,这个点到三角形
的距离相等.(注意:⑴一个三角形的内切圆是惟一的;⑵内心与外心的区别.)
三角形内心的性质: 三角形外心的性质:
【典型例题】
【练习2】如图,点O是△ABC的内心.根据以下条件,求∠BOC的度数.
(1)∠B=50°,∠C=60°; (2)∠A=50°.
解(1): 解(2):
【练习拓展】您能用一个代数式表示∠BOC与∠A之间的数量关系?
【练习3】如图:点I是△ABC的内心,AI交边BC于点D,交△ABC外接圆于点E,连接BE.
试说明:BE=IE.
【练习4】如图,在△ABC中,内切圆I与边BC、CA、AB分别相切于点D、E、F,∠B=60°,∠C=70°,求∠EDF的度数。
【练习5】如图:点I是△ABC的内心,AI交边BC于点D,交△ABC外接圆于点E,连接BE.
△BED和△AEB相似吗?请说明理由.
拓展提高
A
课堂小结:
①三角形的外心是三角形 的交点
①三角形的内心是三角形 线的交点
②三角形的外心到 的距离相等
②三角形的内心到 的距离相等
③三角形的外心 在三角形的
③三角形的内心一定在三角形的
例1、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直棱柱.圆柱的下底面是圆是
直三棱柱上底面等边三角形的内切圆.已知直三棱柱的底面等边三角形边长为3cm,
求圆柱底面的半径。
例2、如图,设△ABC的边BC=a,CA=b,AB=c,设a+b+c=l,n= l,内切圆O和各边分别相切
于D,E,F。求证:(1)AF+BC= l
(2)AD=AF=n-a,BE=BD=n-b,CF=CE=n-c。
例3、已知△ABC的三边BC,AB,AC分别为a,b,c,I为内心,内切圆半径为r,
求△ABC的面积S(用a,b,c,r表示)
例4、已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、AB的长分别为a、b、c,
求其内切圆O的半径长。
A
B
C
a
c
b
r
【练习1】
⑴边长为3,4,5的三角形的内切圆半径是__⑵边长为5,5,6的三角形的内切圆半径是__
如图,△ABC中,I是内心,∠BAC的平分线和△ABC的外接圆相交于点E,与BC交于点D.
求证:(1)IE=BE
设△ABC外接圆半径R=3,IE=2,AE=x,DE=y,当点A在优弧BC上运动时,
求函数y与自变量x间的函数关系式,并指出自变量的取值范围.
O
¤
I
C
B
D
1.本节课从实际问题入手,探索得出三角形内切圆的作法 .
2.通过类比三角形的外接圆与圆的内接三角形概念得出三角形的内切圆、圆的外切三角形概念,
并介绍了多边形的内切圆、圆的外切多边形的概念。
3.学习时要明确“接”和“切”的含义、弄清“内心”与“外心”的区别,
4.利用三角形内心的性质解题时,要注意整体思想的运用,在解决实际问题时,要注意把实际
问题转化为数学问题。
5.5-3 直线和圆的位置关系(三角形的内切圆) 第 4 页 共 4 页
第 5 页 共 4 页
