第四章相似三角形和函数的动态综合题

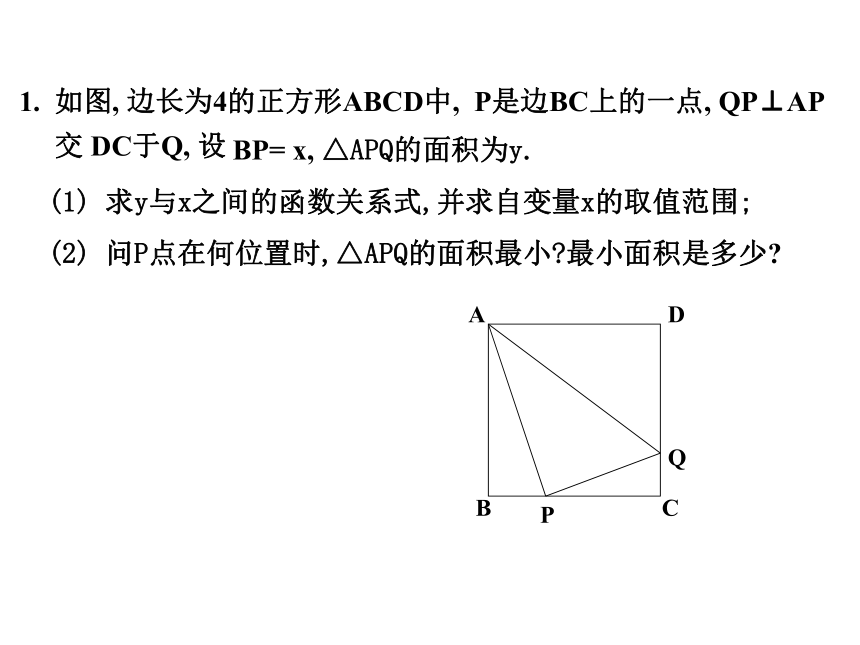
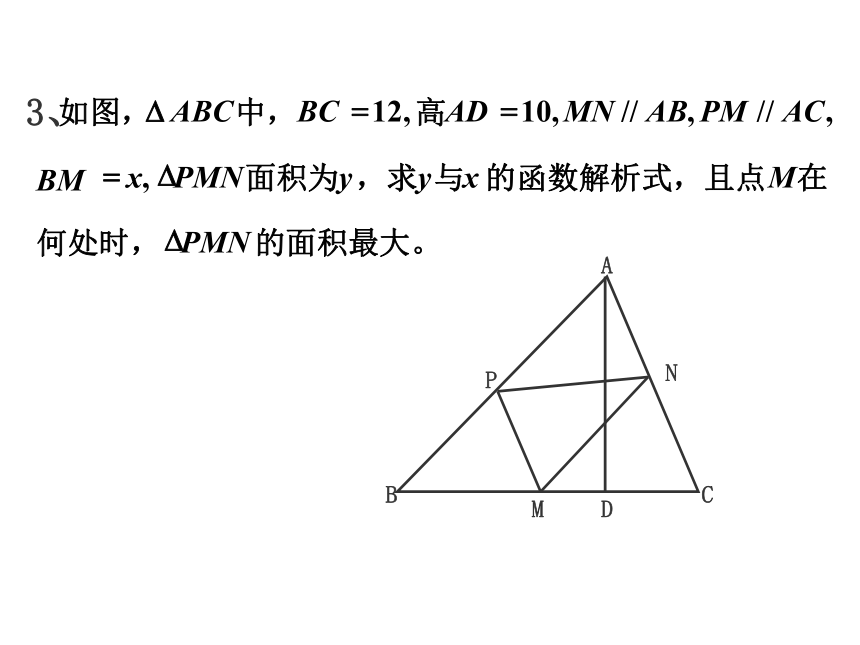
课件13张PPT。相似三角形与函数综合中考提前热身之2. 如图, AD⊥BC, D为垂足, AD=8, BC=10, EFGH是△ABC内接矩形,(H、G是BC上的两个动点,但H不到达点B, G不到达点C) 设 EH=x,EF=y
(1)求y与x之间的函数关系式,并求自变量x的取值范围;
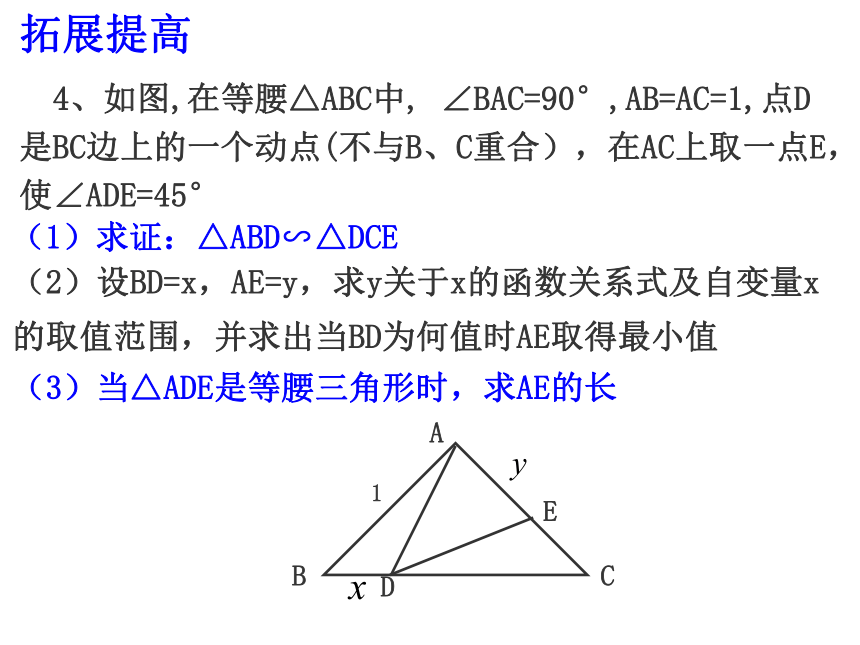
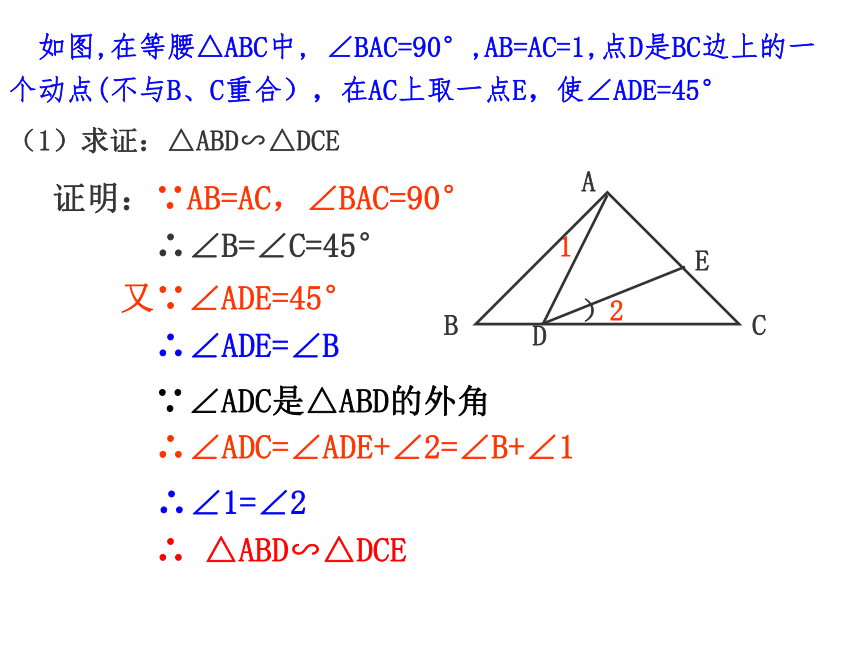
(2)当EF+EH=9时,求矩形EFGH的周长和面积. 4、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（1）求证：△ABD∽△DCE（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值（3）当△ADE是等腰三角形时，求AE的长拓展提高1 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（1）求证：△ABD∽△DCE∵∠ADC是△ABD的外角∴∠ADC=∠ADE+∠2=∠B+∠1）21证明：∵AB=AC，∠BAC=90°∴∠B=∠C=45°又∵∠ADE=45°∴∠ADE=∠B∴∠1=∠2∴ △ABD∽△DCE（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值解：∵△ABD∽△DCE1 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（3）当△ADE是等腰三角形时，求AE的长AD=AEAE=DEDE=AD 如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°1分类讨论5、如图,在直角梯形ABCD中,AB∥CD, ∠A=900,AB=2, AD=5,P是AD上一动点(不与A、D重合),ＰＥ⊥ＢＰ，ＰＥ交ＤＣ于点Ｅ．（１）△ABP与△DPE是否相似？请说明理由；（２）设ＡＰ＝x　ＤＥ=y，求y与x之间的函数关系式,并指出自变量x的取值范围；（3）请你探索在点P运动的过程中，四边形ABED能否构成矩形？如果能，求出AP的长；如果不能，请说明理由；（4）请你探索在点P运动的过程中，△BPE能否成为等腰三角形？如果能，求出AP的长，如果不能，请说明理由。25xy5-x拓展提高6.如图，梯形ABCD中 AD∥BC ，∠ABC=90°，AD=9，BC=12，AB=10，在线段BC上任取一P，作射线PE⊥PD，与线段AB交于点E.（1）试确定CP=5时点E的位置；（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式，并求出自变量x的取值范围.提示：体会这个图形的“模型”作用，将会助你快速解题！拓展提高
7.如图，已知抛物线与x轴交于A、B
两点，与y轴交于C点.
（1）求此抛物线的解析式；
（2）抛物线上有一点P，满足
∠PBC=90°，求点P的坐标；
（3）在（2）的条件下，问在y轴
上是否存在点E，使得以A、O、E
为顶点的三角形与△PBC相似？若
存在，求出点E的坐标；若不存在，
请说明理由.23Q6拓展提高7、如图，平面直角坐标系中，直线AB与x轴y轴分别A（4，0），B（0，3）两点，点C为线段AB上的一动点，过点C作CD⊥x轴于点D.
（1）求直线AB的解析式；
（2）若S梯形OBCD=4.5,求点C的坐标
（3）在第一象限内求作一点P,使得以P，O，B为顶点的三角形与△OBA相似,并求出所有符合条件的点P.
（4）若（3）中，不限定在第一象限，则符合要求的点有　　个（不和A点重合）。