3.1 平均数-2024-2025学年浙教版八年级下册 同步分层作业(含解析)
文档属性
| 名称 | 3.1 平均数-2024-2025学年浙教版八年级下册 同步分层作业(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 867.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 12:23:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.1 平均数 同步分层作业
1.某班五个合作学习小组的人数分别如下:5,5,x,6,8,已知这组数据的平均数是6,则x的值是( )
A.5 B.5.5 C.6 D.7
2.已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
3.在某次数学测验中,小明得了99分,小华得了90分,小龙比小华成绩好,但不超过93分.请估计这三人的平均成绩在( )
A.90分以下 B.94分以上 C.93分~94分之间 D.90分~93分之间
4.现有甲、乙两组数据,数据甲:1,2,3,4.数据乙:2021,2022,2023,2024.若数据甲的平均数为m,乙的平均数为n,则m与n之间的关系为( )
A.m=n B.m=n﹣2020 C.m=n﹣2021 D.m=n﹣2022
5.五位同学中身高最高的是151厘米,最矮的是123厘米,他们的平均身高可能是( )
A.110厘米 B.119厘米 C.123厘米 D.138厘米
6.某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
7.数据﹣2,0,1,﹣2,﹣2的平均数是 .
8.某快递员一周投放快递物品件数为:有3天是20件,有1天是31件,有3天是35件,则本周的日平均投递物品件数为 .
9.某公司招聘一名营销策划人员,候选人成绩由三项素质测试组成.其中,创新能力占50%,综合能力占30%,语言表达能力占20%,如图所示.候选人小李的上述三项成绩依次为90分,80分,85分,则小李的测试成绩是 .
10.某班级课堂从“理解”“归纳”“运用”“综合”“参与”五个方面按2:2:1:2:3对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 分.
11.某班抽查了10名同学的期中考试数学成绩,以108分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,﹣3,+12,﹣7,﹣10,﹣3,﹣8,+1,0,+10.
(1)这10名同学中最高分比最低分多 分;
(2)10名同学中,不低于108分的所占的百分比是多少?
(3)10名同学的数学平均成绩是多少分?
12.某校要在凡凡和莉莉两名同学之间选择一人担任校园活动主持人,对他们综合素质、普通话、才艺展示三方面进行测评,根据综合成绩择优选取.他们的各项成绩如表所示:
测试项目 综合素质 普通话 才艺展示
凡凡 92分 88分 90分
莉莉 90分 91分 93分
根据实际需求,该校规定综合素质、普通话和才艺展示三项测试得分按5:3:2的比例确定最终成绩,应该让谁担任校园活动主持人?
13.某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
14.在一次八年级学生射击训练中,某小组的成绩如下表:
环数 6 7 8 9
人数 1 5 2 2
(1)求出该小组射击的平均成绩;
(2)若8环(含8环)以上为优秀射击手,在全年级400名学生中,估计有多少人可以评为优秀射击手?
15.x1,x2,…,x5的平均数为m;x6,x7…,x20的平均数为n,则 x1,x2,…,x20的平均数为( )
A.m+n B. C. D.
16.设甲糖果的单价为m元/千克,乙糖果的单价为10元/千克,则2千克甲糖果和n千克乙糖果混合而成的什锦糖果的单价为( )
A.元/千克 B.元/千克 C.元/千克 D.元/千克
17.已知两组数据x1,x2,……,xn和y1,y2,……,yn的平均数分别为5和﹣2,则x1+2y1,x2+2y2,……,xn+2yn的平均数为 .
18.某公司销售部有营销人员15人,为了对达到或者超出月销售定额的员工进行表彰,统计了这15人某月的销售量(单位:件)如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数;
(2)假设销售负责人把月销售定额定为280件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
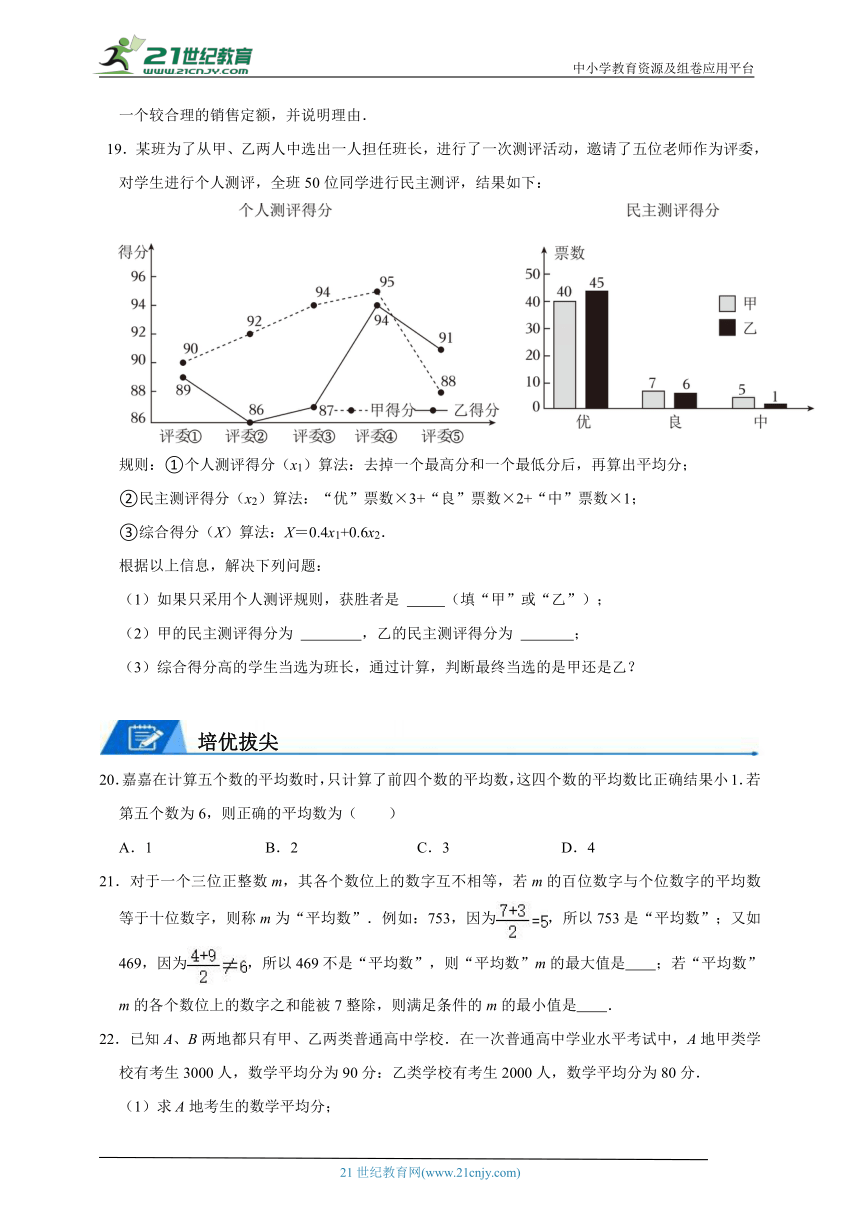
19.某班为了从甲、乙两人中选出一人担任班长,进行了一次测评活动,邀请了五位老师作为评委,对学生进行个人测评,全班50位同学进行民主测评,结果如下:
规则:①个人测评得分(x1)算法:去掉一个最高分和一个最低分后,再算出平均分;
②民主测评得分(x2)算法:“优”票数×3+“良”票数×2+“中”票数×1;
③综合得分(X)算法:X=0.4x1+0.6x2.
根据以上信息,解决下列问题:
(1)如果只采用个人测评规则,获胜者是 (填“甲”或“乙”);
(2)甲的民主测评得分为 ,乙的民主测评得分为 ;
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?
20.嘉嘉在计算五个数的平均数时,只计算了前四个数的平均数,这四个数的平均数比正确结果小1.若第五个数为6,则正确的平均数为( )
A.1 B.2 C.3 D.4
21.对于一个三位正整数m,其各个数位上的数字互不相等,若m的百位数字与个位数字的平均数等于十位数字,则称m为“平均数”.例如:753,因为,所以753是“平均数”;又如469,因为,所以469不是“平均数”,则“平均数”m的最大值是 ;若“平均数”m的各个数位上的数字之和能被7整除,则满足条件的m的最小值是 .
22.已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
23.定义:对于两个正数a和b,a,b的算术平均数,a,b的调和平均数.
【观察归纳】(用“<”、“=”或“>”填空)
①若a=2,b=4,则A H;②若,,则A H;
③若a=6,b=6,则A H;
【猜想验证】
①猜想:对于两个正数a和b,则A H;(用“<”、“=”、“>”、“≥”或“≤”填空)
②请验证你的猜想.
【拓展应用】
甲、乙两港口分别位于长江的上、下游,相距skm,若一艘游轮顺流航行的速度为mkm/h,逆流航行速度为nkm/h(m>n>0),比较该游轮在静水中的速度和往返两港口的平均速度的大小.
答案与解析
1.某班五个合作学习小组的人数分别如下:5,5,x,6,8,已知这组数据的平均数是6,则x的值是( )
A.5 B.5.5 C.6 D.7
【点拨】直接根据数据的平均数是6求解即可.
【解析】解:∵数据的平均数是6,
∴,
解得x=6,
故选:C.
【点睛】本题考查了根据平均数求数据,熟练掌握运算法则是解题的关键.
2.已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
【点拨】先根据算术平均数的定义求出x的值,再设增加数据为m,由增加了一个数据后的平均数仍不变列出关于m的方程,解之即可得出答案.
【解析】解:由题意知,=4,
解得x=3,
所以原数据为2、2、3、5、8,
设增加数据为m,
则=4,
解得m=4,
故选:C.
【点睛】本题主要考查算术平均数,解题的关键是掌握算术平均数的定义.
3.在某次数学测验中,小明得了99分,小华得了90分,小龙比小华成绩好,但不超过93分.请估计这三人的平均成绩在( )
A.90分以下 B.94分以上 C.93分~94分之间 D.90分~93分之间
【点拨】根据小龙的成绩大于90,但不超过93分求出算术平均数,即可解答.
【解析】解:=93,=94,
则这三人的平均成绩在大于93,小于等于94,即这三人的平均成绩在93分~94分之间,
故选:C.
【点睛】本题考查的是算术平均数,解答本题的关键是明确题意、求出相应的算术平均数.
4.现有甲、乙两组数据,数据甲:1,2,3,4.数据乙:2021,2022,2023,2024.若数据甲的平均数为m,乙的平均数为n,则m与n之间的关系为( )
A.m=n B.m=n﹣2020 C.m=n﹣2021 D.m=n﹣2022
【点拨】根据平均数的定义解答即可.
【解析】解:m==2.5,
n==2022.5,
∴n﹣m=2022.5﹣2.5=2020,
∴m=n﹣2020.
故选:B.
【点睛】本题考查算术平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
5.五位同学中身高最高的是151厘米,最矮的是123厘米,他们的平均身高可能是( )
A.110厘米 B.119厘米 C.123厘米 D.138厘米
【点拨】根据算术平均数的意义求解.
【解析】解:∵最大值为151厘米,最小值是123厘米,
∴平均数x的值为:123<x<151,
故选:D.
【点睛】本题考查了算术平均数,理解算术平均数的意义是解题的关键.
6.某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
A.83分 B.80分 C.75分 D.70分
【点拨】根据加权平均数计算公式列出算式,再进行计算即可得出答案.
【解析】解:小颖同学的总成绩为90×30%+80×70%=83(分).
故选:A.
【点睛】本题主要考查加权平均数,熟练掌握加权平均数的定义是解题的关键.
7.数据﹣2,0,1,﹣2,﹣2的平均数是 ﹣1 .
【点拨】将题目中的数据相加,然后除以5,即可得到这组数据的平均数.
【解析】解:(﹣2+0+1﹣2﹣2)÷5
=(﹣5)÷5
=﹣1,
∴数据﹣2,0,1,﹣2,﹣2的平均数是﹣1,
故答案为:﹣1.
【点睛】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
8.某快递员一周投放快递物品件数为:有3天是20件,有1天是31件,有3天是35件,则本周的日平均投递物品件数为 28 .
【点拨】直接利用加权平均数公式计算即可得出答案.
【解析】解:由题意可得,本周的日平均投递物品件数为:=28(件).
故答案为:28.
【点睛】此题主要考查了加权平均数,正确应用公式是解题关键.
9.某公司招聘一名营销策划人员,候选人成绩由三项素质测试组成.其中,创新能力占50%,综合能力占30%,语言表达能力占20%,如图所示.候选人小李的上述三项成绩依次为90分,80分,85分,则小李的测试成绩是 86分 .
【点拨】根据加权平均数的计算方法进行计算即可.
【解析】解:小李的测试成绩是90×50%+80×30%+85×20%=86(分).
故答案为:86分.
【点睛】本题考查加权平均数的计算方法,熟练掌握运算法则是解题的关键.
10.某班级课堂从“理解”“归纳”“运用”“综合”“参与”五个方面按2:2:1:2:3对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 8 分.
【点拨】根据图中的数据和加权平均数的计算方法即可求得该学生的课堂评价成绩.
【解析】解:由图可得,
该学生的课堂评价成绩为:
=
=
=(分),
故答案为:8.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
11.某班抽查了10名同学的期中考试数学成绩,以108分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,﹣3,+12,﹣7,﹣10,﹣3,﹣8,+1,0,+10.
(1)这10名同学中最高分比最低分多 22 分;
(2)10名同学中,不低于108分的所占的百分比是多少?
(3)10名同学的数学平均成绩是多少分?
【点拨】(1)用记录的结果中的最大数减去最小数即可;
(2)由题目中的数据可以知道不低于108分的有几个同学,从而可以计算出不低于108分的所占的百分比;
(3)将题目中的10个数据相加的和除以10再与108相加,即可解答本题.
【解析】解:(1)12﹣(﹣10)=12+10=22(分),
即这10名同学中最高分比最低分多22分,
故答案为:22;
(2)10名同学中,不低于108分的有5名同学,
=50%,
答:10名同学中,不低于108分的所占的百分比是50%;
(3)108+(+8﹣3+12﹣7﹣10﹣3﹣8+1+0+10)
=108+0
=108(分),
答:10名同学的数学平均成绩是108分.
【点睛】本题考查正数和负数以及算术平均数,解题的关键是明确正数和负数在题目中表示的含义.
12.某校要在凡凡和莉莉两名同学之间选择一人担任校园活动主持人,对他们综合素质、普通话、才艺展示三方面进行测评,根据综合成绩择优选取.他们的各项成绩如表所示:
测试项目 综合素质 普通话 才艺展示
凡凡 92分 88分 90分
莉莉 90分 91分 93分
根据实际需求,该校规定综合素质、普通话和才艺展示三项测试得分按5:3:2的比例确定最终成绩,应该让谁担任校园活动主持人?
【点拨】根据加权平均数的计算方法计算,再根据加权平均数的定义作出抉择即可.
【解析】解:凡凡:(分),
莉莉:(分),
90.9>90.4,
答:应该让莉莉担任校园活动主持人.
【点睛】本题考查了加权平均数的知识,熟练掌握加权平均数的计算方法是解题的关键.
13.某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
【点拨】(1)每个选手去掉一个最高分,再去掉一个最低分,求出剩下三个数的平均数即可;
(2)分别求出甲乙的民主测评得分即可.
(3)根据加权平均数的公式,计算即可判断.
【解析】解:(1)甲演讲答辩平均分=92(分),
乙演讲答辩平均分:=89(分),
(2)甲民主测评得分:40×2+7×1=87(分),
乙民主测评得分,42×2+4×1=88(分).
(4)甲综合得分=90(分),
乙综合得分=88.6(分),
∵90>88.6,
∴应选甲同学当班长.
【点睛】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.解题的关键是理解题意,理解“权”对平均数的影响.
14.在一次八年级学生射击训练中,某小组的成绩如下表:
环数 6 7 8 9
人数 1 5 2 2
(1)求出该小组射击的平均成绩;
(2)若8环(含8环)以上为优秀射击手,在全年级400名学生中,估计有多少人可以评为优秀射击手?
【点拨】(1)根据平均数的计算公式进行计算即可;
(2)用400乘以优秀射击手所占的百分比即可得出答案.
【解析】解:(1)该小组射击的平均成绩是:(6×1+7×5+8×2+9×2)÷(1+5+2+2)=7.5(环);
(2)400×=160(人),
答:估计有160人可以评为优秀射击手.
【点睛】此题考查了加权平均数和用样本估计总体,掌握用样本估计总体和平均数的计算公式是本题的关键.
15.x1,x2,…,x5的平均数为m;x6,x7…,x20的平均数为n,则 x1,x2,…,x20的平均数为( )
A.m+n B. C. D.
【点拨】利用平均数的定义直接求解.
【解析】解:∵x1,x2,…,x5的平均数为m;x6,x7…,x20的平均数为n,
∴x1,x2,…,x5的和为5m;x6,x7…,x20的和为15n,
∴x1,x2,…,x20的平均数为.
故选:D.
【点睛】本题考查平均数的定义,平均数的求法等基础知识,考查运算求解能力,是基础题.
16.设甲糖果的单价为m元/千克,乙糖果的单价为10元/千克,则2千克甲糖果和n千克乙糖果混合而成的什锦糖果的单价为( )
A.元/千克 B.元/千克 C.元/千克 D.元/千克
【点拨】混合前后总数量和总价不变.混合的糖果的单价=总价÷总数量.
【解析】解:依题意得,混合后糖果总价为(2m+10n),总质量为(2+n)千克,
故混合的糖果的单价=(元/千克).
故选:C.
【点睛】本题考查加权平均数,注意混合什锦糖单价=甲种糖果和乙种糖果的总价钱÷混合糖果的重量.
17.已知两组数据x1,x2,……,xn和y1,y2,……,yn的平均数分别为5和﹣2,则x1+2y1,x2+2y2,……,xn+2yn的平均数为 1 .
【点拨】根据两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别为5和﹣2,可以计算出x1+2y1,x2+2y2,……,xn+2yn的平均数.
【解析】解:∵两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别为5和﹣2,
∴x1+x2+……+xn=5n,y1+y2+……+yn=﹣2n,
∴x1+2y1,x2+2y2,…,xn+2yn的平均数为:(x1+2y1+x2+2y2+…+xn+2yn)
=[(x1+x2+…+xn)+2(y1+y2+…+yn)]
=[5n+2×(﹣2n)]
=×(5n﹣4n)
=×n
=1.
故答案为:1.
【点睛】本题考查算术平均数,解答本题的关键是明确题意,求出相应的平均数.
18.某公司销售部有营销人员15人,为了对达到或者超出月销售定额的员工进行表彰,统计了这15人某月的销售量(单位:件)如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数;
(2)假设销售负责人把月销售定额定为280件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
【点拨】(1)平均数是指在一组数据中所有数据之和再除以数据的个数.
(2)根据表中数据和平均数、中位数和众数的意义回答.
【解析】解:(1)平均数是:(1400+880+270×3+150×6+130×3+120)=300(件);
(2)不合理.
因为15人中有13人的销售额不到300件,300件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平.销售额定为150件合适些,因为150件既是中位数,又是众数,是大部分人能达到的定额.
【点睛】此题考查了学生对中位数,众数,平均数的掌握情况.它们都是反映数据集中趋势的指标.
19.某班为了从甲、乙两人中选出一人担任班长,进行了一次测评活动,邀请了五位老师作为评委,对学生进行个人测评,全班50位同学进行民主测评,结果如下:
规则:①个人测评得分(x1)算法:去掉一个最高分和一个最低分后,再算出平均分;
②民主测评得分(x2)算法:“优”票数×3+“良”票数×2+“中”票数×1;
③综合得分(X)算法:X=0.4x1+0.6x2.
根据以上信息,解决下列问题:
(1)如果只采用个人测评规则,获胜者是 甲 (填“甲”或“乙”);
(2)甲的民主测评得分为 139分 ,乙的民主测评得分为 148分 ;
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?
【点拨】(1)根据个人测评得分的算法计算出甲和乙的得分即可得出答案;
(2)根据民主测评得分算法计算即可;
(3)根据综合得分算法计算出甲和乙的得分即可得出答案.
【解析】解:(1)甲的个人测评得分为=92(分),乙的个人测评得分为=89(分),
∵92>89
∴获胜者是甲;
故答案为:甲;
(2)甲的民主测评得分为40×3+7×2+5×1=139(分),
乙的民主测评得分为45×3+6×2+1×1=148(分),
故答案为:139分,148分;
(3)甲的综合得分为0.4×92+0.6×139=120.2(分),
乙的综合得分为0.4×89+0.6×148=124.4(分),
∵124.4>120.2,
∴最终当选的是乙.
【点睛】本题考查了求平均数,加权平均数,条形统计图,熟练掌握平均数的计算方法是解题的关键.
20.嘉嘉在计算五个数的平均数时,只计算了前四个数的平均数,这四个数的平均数比正确结果小1.若第五个数为6,则正确的平均数为( )
A.1 B.2 C.3 D.4
【点拨】设正确的平均数为x,根据四个数的平均数比正确结果小1得到前四个数的和为4(x﹣1),再根据平均数的正确求法列方程,然后解方程即可.
【解析】解:设正确的平均数为x,
由题意可得:,
解得x=2,
故选:B.
【点睛】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
21.对于一个三位正整数m,其各个数位上的数字互不相等,若m的百位数字与个位数字的平均数等于十位数字,则称m为“平均数”.例如:753,因为,所以753是“平均数”;又如469,因为,所以469不是“平均数”,则“平均数”m的最大值是 987 ;若“平均数”m的各个数位上的数字之和能被7整除,则满足条件的m的最小值是 579 .
【点拨】根据“平均数”的定义可知,若“平均数”m取得最大值,则百位数字是9,十位数字是8,则个位数字是7;再根据“平均数”m的各个数位上的数字之和能被7整除,即可得到满足条件的m的最小值.
【解析】解:由题意可得,“平均数”m的最大值是987;
设三位数m的十位数字为a,则百位数字和个位数字之和为2a,
∵“平均数”m的各个数位上的数字之和能被7整除,
∴a+2a=3a能被7整除,
∴a最小是7,
∴满足条件的m的最小值是579.
故答案为:987,579.
【点睛】本题考查整式的加减,解答本题的关键是明确题意,利用新定义解答.
22.已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
【点拨】(1)根据平均数的概念求解即可;
(2)根据平均数的意义求解即可.
【解析】解:(1)由题意,得A地考生的数学平均分为(分);
(2)不能.举例如下:
如B地甲类学校有考生1000人,乙类学校有考生3000人,则B地考生的数学平均分为
(分),
∵85<86,
∴不能判断B地考生数学平均分一定比A地考生数学平均分高.
【点睛】本题考查加权平均数等基础知识,掌握加权平均数是解题的关键.
23.定义:对于两个正数a和b,a,b的算术平均数,a,b的调和平均数.
【观察归纳】(用“<”、“=”或“>”填空)
①若a=2,b=4,则A > H;②若,,则A > H;
③若a=6,b=6,则A = H;
【猜想验证】
①猜想:对于两个正数a和b,则A ≥ H;(用“<”、“=”、“>”、“≥”或“≤”填空)
②请验证你的猜想.
【拓展应用】
甲、乙两港口分别位于长江的上、下游,相距skm,若一艘游轮顺流航行的速度为mkm/h,逆流航行速度为nkm/h(m>n>0),比较该游轮在静水中的速度和往返两港口的平均速度的大小.
【点拨】观察归纳:①根据新定义进行计算比较即可;
②根据新定义进行计算比较即可;
③根据新定义进行计算比较即可;
猜想验证:①根据新定义和①②进行猜想比较即可;
②运用作差法进行比较即可;
扩展应用:先表示出游轮在静水中的速度和往返两港口的平均速度,然后再运用猜想验证中的结论进行解答即可.
【解析】解:观察归纳:①a=2,b=4,则A==3,
H==,
∴A>H;
故答案为:>;
②若,,则A==,
H==,
∴A>H;
故答案为:>;
③若a=6,b=6,则A==6,
H==6,
∴A=H,
故答案为:=;
猜想验证:①根据观察归纳可猜想:A≥H,
故答案为:≥;
②证明:A﹣H
=
=
=,
∵两个正数a和b,
∴(a﹣b)2≥0,2(a+b)>0,
∴≥0,
∴A≥H.
扩展应用:
静水中的速度为:(km/h);
往返两港口的平均速度:=(km/h);
∵m>n>0,
∴由猜想验证的结论可得:,
∴该游轮在静水中的速度大于等于往返两港口的平均速度.
【点睛】本题主要考查的是算术平均数,理解新定义是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
3.1 平均数 同步分层作业
1.某班五个合作学习小组的人数分别如下:5,5,x,6,8,已知这组数据的平均数是6,则x的值是( )
A.5 B.5.5 C.6 D.7
2.已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
3.在某次数学测验中,小明得了99分,小华得了90分,小龙比小华成绩好,但不超过93分.请估计这三人的平均成绩在( )
A.90分以下 B.94分以上 C.93分~94分之间 D.90分~93分之间
4.现有甲、乙两组数据,数据甲:1,2,3,4.数据乙:2021,2022,2023,2024.若数据甲的平均数为m,乙的平均数为n,则m与n之间的关系为( )
A.m=n B.m=n﹣2020 C.m=n﹣2021 D.m=n﹣2022
5.五位同学中身高最高的是151厘米,最矮的是123厘米,他们的平均身高可能是( )
A.110厘米 B.119厘米 C.123厘米 D.138厘米
6.某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
7.数据﹣2,0,1,﹣2,﹣2的平均数是 .
8.某快递员一周投放快递物品件数为:有3天是20件,有1天是31件,有3天是35件,则本周的日平均投递物品件数为 .
9.某公司招聘一名营销策划人员,候选人成绩由三项素质测试组成.其中,创新能力占50%,综合能力占30%,语言表达能力占20%,如图所示.候选人小李的上述三项成绩依次为90分,80分,85分,则小李的测试成绩是 .
10.某班级课堂从“理解”“归纳”“运用”“综合”“参与”五个方面按2:2:1:2:3对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 分.
11.某班抽查了10名同学的期中考试数学成绩,以108分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,﹣3,+12,﹣7,﹣10,﹣3,﹣8,+1,0,+10.
(1)这10名同学中最高分比最低分多 分;
(2)10名同学中,不低于108分的所占的百分比是多少?
(3)10名同学的数学平均成绩是多少分?
12.某校要在凡凡和莉莉两名同学之间选择一人担任校园活动主持人,对他们综合素质、普通话、才艺展示三方面进行测评,根据综合成绩择优选取.他们的各项成绩如表所示:
测试项目 综合素质 普通话 才艺展示
凡凡 92分 88分 90分
莉莉 90分 91分 93分
根据实际需求,该校规定综合素质、普通话和才艺展示三项测试得分按5:3:2的比例确定最终成绩,应该让谁担任校园活动主持人?
13.某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
14.在一次八年级学生射击训练中,某小组的成绩如下表:
环数 6 7 8 9
人数 1 5 2 2
(1)求出该小组射击的平均成绩;
(2)若8环(含8环)以上为优秀射击手,在全年级400名学生中,估计有多少人可以评为优秀射击手?
15.x1,x2,…,x5的平均数为m;x6,x7…,x20的平均数为n,则 x1,x2,…,x20的平均数为( )
A.m+n B. C. D.
16.设甲糖果的单价为m元/千克,乙糖果的单价为10元/千克,则2千克甲糖果和n千克乙糖果混合而成的什锦糖果的单价为( )
A.元/千克 B.元/千克 C.元/千克 D.元/千克
17.已知两组数据x1,x2,……,xn和y1,y2,……,yn的平均数分别为5和﹣2,则x1+2y1,x2+2y2,……,xn+2yn的平均数为 .
18.某公司销售部有营销人员15人,为了对达到或者超出月销售定额的员工进行表彰,统计了这15人某月的销售量(单位:件)如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数;
(2)假设销售负责人把月销售定额定为280件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
19.某班为了从甲、乙两人中选出一人担任班长,进行了一次测评活动,邀请了五位老师作为评委,对学生进行个人测评,全班50位同学进行民主测评,结果如下:
规则:①个人测评得分(x1)算法:去掉一个最高分和一个最低分后,再算出平均分;
②民主测评得分(x2)算法:“优”票数×3+“良”票数×2+“中”票数×1;
③综合得分(X)算法:X=0.4x1+0.6x2.
根据以上信息,解决下列问题:
(1)如果只采用个人测评规则,获胜者是 (填“甲”或“乙”);
(2)甲的民主测评得分为 ,乙的民主测评得分为 ;
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?
20.嘉嘉在计算五个数的平均数时,只计算了前四个数的平均数,这四个数的平均数比正确结果小1.若第五个数为6,则正确的平均数为( )
A.1 B.2 C.3 D.4
21.对于一个三位正整数m,其各个数位上的数字互不相等,若m的百位数字与个位数字的平均数等于十位数字,则称m为“平均数”.例如:753,因为,所以753是“平均数”;又如469,因为,所以469不是“平均数”,则“平均数”m的最大值是 ;若“平均数”m的各个数位上的数字之和能被7整除,则满足条件的m的最小值是 .
22.已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
23.定义:对于两个正数a和b,a,b的算术平均数,a,b的调和平均数.
【观察归纳】(用“<”、“=”或“>”填空)
①若a=2,b=4,则A H;②若,,则A H;
③若a=6,b=6,则A H;
【猜想验证】
①猜想:对于两个正数a和b,则A H;(用“<”、“=”、“>”、“≥”或“≤”填空)
②请验证你的猜想.
【拓展应用】
甲、乙两港口分别位于长江的上、下游,相距skm,若一艘游轮顺流航行的速度为mkm/h,逆流航行速度为nkm/h(m>n>0),比较该游轮在静水中的速度和往返两港口的平均速度的大小.
答案与解析
1.某班五个合作学习小组的人数分别如下:5,5,x,6,8,已知这组数据的平均数是6,则x的值是( )
A.5 B.5.5 C.6 D.7
【点拨】直接根据数据的平均数是6求解即可.
【解析】解:∵数据的平均数是6,
∴,
解得x=6,
故选:C.
【点睛】本题考查了根据平均数求数据,熟练掌握运算法则是解题的关键.
2.已知五个数据:2,2,x,5,8的平均数是4,现增加了一个数据后的平均数仍不变,则增加的这个数据是( )
A.0 B.2 C.4 D.5
【点拨】先根据算术平均数的定义求出x的值,再设增加数据为m,由增加了一个数据后的平均数仍不变列出关于m的方程,解之即可得出答案.
【解析】解:由题意知,=4,
解得x=3,
所以原数据为2、2、3、5、8,
设增加数据为m,
则=4,
解得m=4,
故选:C.
【点睛】本题主要考查算术平均数,解题的关键是掌握算术平均数的定义.
3.在某次数学测验中,小明得了99分,小华得了90分,小龙比小华成绩好,但不超过93分.请估计这三人的平均成绩在( )
A.90分以下 B.94分以上 C.93分~94分之间 D.90分~93分之间
【点拨】根据小龙的成绩大于90,但不超过93分求出算术平均数,即可解答.
【解析】解:=93,=94,
则这三人的平均成绩在大于93,小于等于94,即这三人的平均成绩在93分~94分之间,
故选:C.
【点睛】本题考查的是算术平均数,解答本题的关键是明确题意、求出相应的算术平均数.
4.现有甲、乙两组数据,数据甲:1,2,3,4.数据乙:2021,2022,2023,2024.若数据甲的平均数为m,乙的平均数为n,则m与n之间的关系为( )
A.m=n B.m=n﹣2020 C.m=n﹣2021 D.m=n﹣2022
【点拨】根据平均数的定义解答即可.
【解析】解:m==2.5,
n==2022.5,
∴n﹣m=2022.5﹣2.5=2020,
∴m=n﹣2020.
故选:B.
【点睛】本题考查算术平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
5.五位同学中身高最高的是151厘米,最矮的是123厘米,他们的平均身高可能是( )
A.110厘米 B.119厘米 C.123厘米 D.138厘米
【点拨】根据算术平均数的意义求解.
【解析】解:∵最大值为151厘米,最小值是123厘米,
∴平均数x的值为:123<x<151,
故选:D.
【点睛】本题考查了算术平均数,理解算术平均数的意义是解题的关键.
6.某校举行校园十佳歌手大赛,小颖同学的初赛成绩为90分,复赛成绩为80分.若总成绩按初赛成绩占30%,复赛成绩占70%来计算,则小颖同学的总成绩为( )
A.83分 B.80分 C.75分 D.70分
【点拨】根据加权平均数计算公式列出算式,再进行计算即可得出答案.
【解析】解:小颖同学的总成绩为90×30%+80×70%=83(分).
故选:A.
【点睛】本题主要考查加权平均数,熟练掌握加权平均数的定义是解题的关键.
7.数据﹣2,0,1,﹣2,﹣2的平均数是 ﹣1 .
【点拨】将题目中的数据相加,然后除以5,即可得到这组数据的平均数.
【解析】解:(﹣2+0+1﹣2﹣2)÷5
=(﹣5)÷5
=﹣1,
∴数据﹣2,0,1,﹣2,﹣2的平均数是﹣1,
故答案为:﹣1.
【点睛】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
8.某快递员一周投放快递物品件数为:有3天是20件,有1天是31件,有3天是35件,则本周的日平均投递物品件数为 28 .
【点拨】直接利用加权平均数公式计算即可得出答案.
【解析】解:由题意可得,本周的日平均投递物品件数为:=28(件).
故答案为:28.
【点睛】此题主要考查了加权平均数,正确应用公式是解题关键.
9.某公司招聘一名营销策划人员,候选人成绩由三项素质测试组成.其中,创新能力占50%,综合能力占30%,语言表达能力占20%,如图所示.候选人小李的上述三项成绩依次为90分,80分,85分,则小李的测试成绩是 86分 .
【点拨】根据加权平均数的计算方法进行计算即可.
【解析】解:小李的测试成绩是90×50%+80×30%+85×20%=86(分).
故答案为:86分.
【点睛】本题考查加权平均数的计算方法,熟练掌握运算法则是解题的关键.
10.某班级课堂从“理解”“归纳”“运用”“综合”“参与”五个方面按2:2:1:2:3对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 8 分.
【点拨】根据图中的数据和加权平均数的计算方法即可求得该学生的课堂评价成绩.
【解析】解:由图可得,
该学生的课堂评价成绩为:
=
=
=(分),
故答案为:8.
【点睛】本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
11.某班抽查了10名同学的期中考试数学成绩,以108分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,﹣3,+12,﹣7,﹣10,﹣3,﹣8,+1,0,+10.
(1)这10名同学中最高分比最低分多 22 分;
(2)10名同学中,不低于108分的所占的百分比是多少?
(3)10名同学的数学平均成绩是多少分?
【点拨】(1)用记录的结果中的最大数减去最小数即可;
(2)由题目中的数据可以知道不低于108分的有几个同学,从而可以计算出不低于108分的所占的百分比;
(3)将题目中的10个数据相加的和除以10再与108相加,即可解答本题.
【解析】解:(1)12﹣(﹣10)=12+10=22(分),
即这10名同学中最高分比最低分多22分,
故答案为:22;
(2)10名同学中,不低于108分的有5名同学,
=50%,
答:10名同学中,不低于108分的所占的百分比是50%;
(3)108+(+8﹣3+12﹣7﹣10﹣3﹣8+1+0+10)
=108+0
=108(分),
答:10名同学的数学平均成绩是108分.
【点睛】本题考查正数和负数以及算术平均数,解题的关键是明确正数和负数在题目中表示的含义.
12.某校要在凡凡和莉莉两名同学之间选择一人担任校园活动主持人,对他们综合素质、普通话、才艺展示三方面进行测评,根据综合成绩择优选取.他们的各项成绩如表所示:
测试项目 综合素质 普通话 才艺展示
凡凡 92分 88分 90分
莉莉 90分 91分 93分
根据实际需求,该校规定综合素质、普通话和才艺展示三项测试得分按5:3:2的比例确定最终成绩,应该让谁担任校园活动主持人?
【点拨】根据加权平均数的计算方法计算,再根据加权平均数的定义作出抉择即可.
【解析】解:凡凡:(分),
莉莉:(分),
90.9>90.4,
答:应该让莉莉担任校园活动主持人.
【点睛】本题考查了加权平均数的知识,熟练掌握加权平均数的计算方法是解题的关键.
13.某班为从甲、乙两名同学中选出班长,进行了一次演讲答辩和民主测评.其中A,B,C,D,E五位老师作为评委,对演讲答辩情况进行评价,结果如表,另全班50位同学参加民主测评进行投票,结果如图.
演讲答辩得分表(单位:分)
A B C D E
甲 89 91 92 94 93
乙 90 86 85 91 94
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;测评民主得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分.
(1)求甲、乙两名同学各自演讲答辩得分的平均分;
(2)求甲、乙两名同学的民主测评得分;
(3)若按演讲答辩得分和民主测评得分6:4的比例计算两名同学的综合得分,则应选哪位同学当班长?并说明理由.
【点拨】(1)每个选手去掉一个最高分,再去掉一个最低分,求出剩下三个数的平均数即可;
(2)分别求出甲乙的民主测评得分即可.
(3)根据加权平均数的公式,计算即可判断.
【解析】解:(1)甲演讲答辩平均分=92(分),
乙演讲答辩平均分:=89(分),
(2)甲民主测评得分:40×2+7×1=87(分),
乙民主测评得分,42×2+4×1=88(分).
(4)甲综合得分=90(分),
乙综合得分=88.6(分),
∵90>88.6,
∴应选甲同学当班长.
【点睛】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.解题的关键是理解题意,理解“权”对平均数的影响.
14.在一次八年级学生射击训练中,某小组的成绩如下表:
环数 6 7 8 9
人数 1 5 2 2
(1)求出该小组射击的平均成绩;
(2)若8环(含8环)以上为优秀射击手,在全年级400名学生中,估计有多少人可以评为优秀射击手?
【点拨】(1)根据平均数的计算公式进行计算即可;
(2)用400乘以优秀射击手所占的百分比即可得出答案.
【解析】解:(1)该小组射击的平均成绩是:(6×1+7×5+8×2+9×2)÷(1+5+2+2)=7.5(环);
(2)400×=160(人),
答:估计有160人可以评为优秀射击手.
【点睛】此题考查了加权平均数和用样本估计总体,掌握用样本估计总体和平均数的计算公式是本题的关键.
15.x1,x2,…,x5的平均数为m;x6,x7…,x20的平均数为n,则 x1,x2,…,x20的平均数为( )
A.m+n B. C. D.
【点拨】利用平均数的定义直接求解.
【解析】解:∵x1,x2,…,x5的平均数为m;x6,x7…,x20的平均数为n,
∴x1,x2,…,x5的和为5m;x6,x7…,x20的和为15n,
∴x1,x2,…,x20的平均数为.
故选:D.
【点睛】本题考查平均数的定义,平均数的求法等基础知识,考查运算求解能力,是基础题.
16.设甲糖果的单价为m元/千克,乙糖果的单价为10元/千克,则2千克甲糖果和n千克乙糖果混合而成的什锦糖果的单价为( )
A.元/千克 B.元/千克 C.元/千克 D.元/千克
【点拨】混合前后总数量和总价不变.混合的糖果的单价=总价÷总数量.
【解析】解:依题意得,混合后糖果总价为(2m+10n),总质量为(2+n)千克,
故混合的糖果的单价=(元/千克).
故选:C.
【点睛】本题考查加权平均数,注意混合什锦糖单价=甲种糖果和乙种糖果的总价钱÷混合糖果的重量.
17.已知两组数据x1,x2,……,xn和y1,y2,……,yn的平均数分别为5和﹣2,则x1+2y1,x2+2y2,……,xn+2yn的平均数为 1 .
【点拨】根据两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别为5和﹣2,可以计算出x1+2y1,x2+2y2,……,xn+2yn的平均数.
【解析】解:∵两组数据x1,x2,…,xn和y1,y2,…,yn的平均数分别为5和﹣2,
∴x1+x2+……+xn=5n,y1+y2+……+yn=﹣2n,
∴x1+2y1,x2+2y2,…,xn+2yn的平均数为:(x1+2y1+x2+2y2+…+xn+2yn)
=[(x1+x2+…+xn)+2(y1+y2+…+yn)]
=[5n+2×(﹣2n)]
=×(5n﹣4n)
=×n
=1.
故答案为:1.
【点睛】本题考查算术平均数,解答本题的关键是明确题意,求出相应的平均数.
18.某公司销售部有营销人员15人,为了对达到或者超出月销售定额的员工进行表彰,统计了这15人某月的销售量(单位:件)如下:
每人销售件数 1400 880 270 150 130 120
人数 1 1 3 6 3 1
(1)求这15位营销人员该月销售量的平均数;
(2)假设销售负责人把月销售定额定为280件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
【点拨】(1)平均数是指在一组数据中所有数据之和再除以数据的个数.
(2)根据表中数据和平均数、中位数和众数的意义回答.
【解析】解:(1)平均数是:(1400+880+270×3+150×6+130×3+120)=300(件);
(2)不合理.
因为15人中有13人的销售额不到300件,300件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平.销售额定为150件合适些,因为150件既是中位数,又是众数,是大部分人能达到的定额.
【点睛】此题考查了学生对中位数,众数,平均数的掌握情况.它们都是反映数据集中趋势的指标.
19.某班为了从甲、乙两人中选出一人担任班长,进行了一次测评活动,邀请了五位老师作为评委,对学生进行个人测评,全班50位同学进行民主测评,结果如下:
规则:①个人测评得分(x1)算法:去掉一个最高分和一个最低分后,再算出平均分;
②民主测评得分(x2)算法:“优”票数×3+“良”票数×2+“中”票数×1;
③综合得分(X)算法:X=0.4x1+0.6x2.
根据以上信息,解决下列问题:
(1)如果只采用个人测评规则,获胜者是 甲 (填“甲”或“乙”);
(2)甲的民主测评得分为 139分 ,乙的民主测评得分为 148分 ;
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?
【点拨】(1)根据个人测评得分的算法计算出甲和乙的得分即可得出答案;
(2)根据民主测评得分算法计算即可;
(3)根据综合得分算法计算出甲和乙的得分即可得出答案.
【解析】解:(1)甲的个人测评得分为=92(分),乙的个人测评得分为=89(分),
∵92>89
∴获胜者是甲;
故答案为:甲;
(2)甲的民主测评得分为40×3+7×2+5×1=139(分),
乙的民主测评得分为45×3+6×2+1×1=148(分),
故答案为:139分,148分;
(3)甲的综合得分为0.4×92+0.6×139=120.2(分),
乙的综合得分为0.4×89+0.6×148=124.4(分),
∵124.4>120.2,
∴最终当选的是乙.
【点睛】本题考查了求平均数,加权平均数,条形统计图,熟练掌握平均数的计算方法是解题的关键.
20.嘉嘉在计算五个数的平均数时,只计算了前四个数的平均数,这四个数的平均数比正确结果小1.若第五个数为6,则正确的平均数为( )
A.1 B.2 C.3 D.4
【点拨】设正确的平均数为x,根据四个数的平均数比正确结果小1得到前四个数的和为4(x﹣1),再根据平均数的正确求法列方程,然后解方程即可.
【解析】解:设正确的平均数为x,
由题意可得:,
解得x=2,
故选:B.
【点睛】本题考查算术平均数,解答本题的关键是明确算术平均数的计算方法.
21.对于一个三位正整数m,其各个数位上的数字互不相等,若m的百位数字与个位数字的平均数等于十位数字,则称m为“平均数”.例如:753,因为,所以753是“平均数”;又如469,因为,所以469不是“平均数”,则“平均数”m的最大值是 987 ;若“平均数”m的各个数位上的数字之和能被7整除,则满足条件的m的最小值是 579 .
【点拨】根据“平均数”的定义可知,若“平均数”m取得最大值,则百位数字是9,十位数字是8,则个位数字是7;再根据“平均数”m的各个数位上的数字之和能被7整除,即可得到满足条件的m的最小值.
【解析】解:由题意可得,“平均数”m的最大值是987;
设三位数m的十位数字为a,则百位数字和个位数字之和为2a,
∵“平均数”m的各个数位上的数字之和能被7整除,
∴a+2a=3a能被7整除,
∴a最小是7,
∴满足条件的m的最小值是579.
故答案为:987,579.
【点睛】本题考查整式的加减,解答本题的关键是明确题意,利用新定义解答.
22.已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
【点拨】(1)根据平均数的概念求解即可;
(2)根据平均数的意义求解即可.
【解析】解:(1)由题意,得A地考生的数学平均分为(分);
(2)不能.举例如下:
如B地甲类学校有考生1000人,乙类学校有考生3000人,则B地考生的数学平均分为
(分),
∵85<86,
∴不能判断B地考生数学平均分一定比A地考生数学平均分高.
【点睛】本题考查加权平均数等基础知识,掌握加权平均数是解题的关键.
23.定义:对于两个正数a和b,a,b的算术平均数,a,b的调和平均数.
【观察归纳】(用“<”、“=”或“>”填空)
①若a=2,b=4,则A > H;②若,,则A > H;
③若a=6,b=6,则A = H;
【猜想验证】
①猜想:对于两个正数a和b,则A ≥ H;(用“<”、“=”、“>”、“≥”或“≤”填空)
②请验证你的猜想.
【拓展应用】
甲、乙两港口分别位于长江的上、下游,相距skm,若一艘游轮顺流航行的速度为mkm/h,逆流航行速度为nkm/h(m>n>0),比较该游轮在静水中的速度和往返两港口的平均速度的大小.
【点拨】观察归纳:①根据新定义进行计算比较即可;
②根据新定义进行计算比较即可;
③根据新定义进行计算比较即可;
猜想验证:①根据新定义和①②进行猜想比较即可;
②运用作差法进行比较即可;
扩展应用:先表示出游轮在静水中的速度和往返两港口的平均速度,然后再运用猜想验证中的结论进行解答即可.
【解析】解:观察归纳:①a=2,b=4,则A==3,
H==,
∴A>H;
故答案为:>;
②若,,则A==,
H==,
∴A>H;
故答案为:>;
③若a=6,b=6,则A==6,
H==6,
∴A=H,
故答案为:=;
猜想验证:①根据观察归纳可猜想:A≥H,
故答案为:≥;
②证明:A﹣H
=
=
=,
∵两个正数a和b,
∴(a﹣b)2≥0,2(a+b)>0,
∴≥0,
∴A≥H.
扩展应用:
静水中的速度为:(km/h);
往返两港口的平均速度:=(km/h);
∵m>n>0,
∴由猜想验证的结论可得:,
∴该游轮在静水中的速度大于等于往返两港口的平均速度.
【点睛】本题主要考查的是算术平均数,理解新定义是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
