第六章反比例函数单元测试卷(含解析)
文档属性
| 名称 | 第六章反比例函数单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 632.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章反比例函数单元测试卷浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2)
B.图象位于第二、四象限
C.x<0,则y>0
D.y随x的增大而增大
2.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
3.反比例函数中,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1,点P(2,m)在此反比例函数图象上,则m的值为( )
A.2 B.﹣2 C.8 D.﹣8
4.正比例函数与反比例函数的图象相交于A、B两点,其中点A的坐标为(3,2),那么点B的坐标为( )
A.(﹣3,﹣2) B.(﹣3,2) C.(﹣2,﹣3) D.(2,3)
5.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
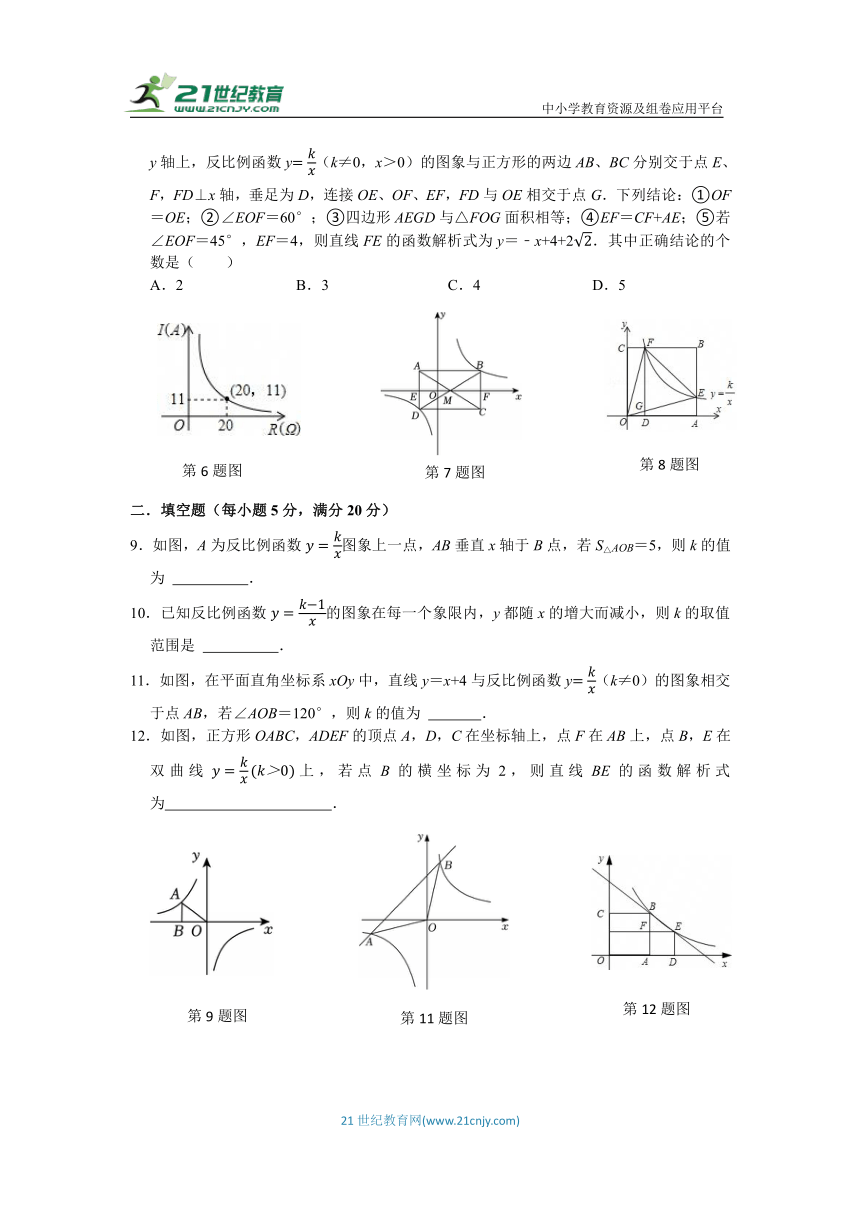
6.电路上在电压保持不变的条件下,电流I(A)与电阻R(Ω)成反比例关系,I与R的函数图象如图,I关于R函数解析式是( )
A. B. C. D.
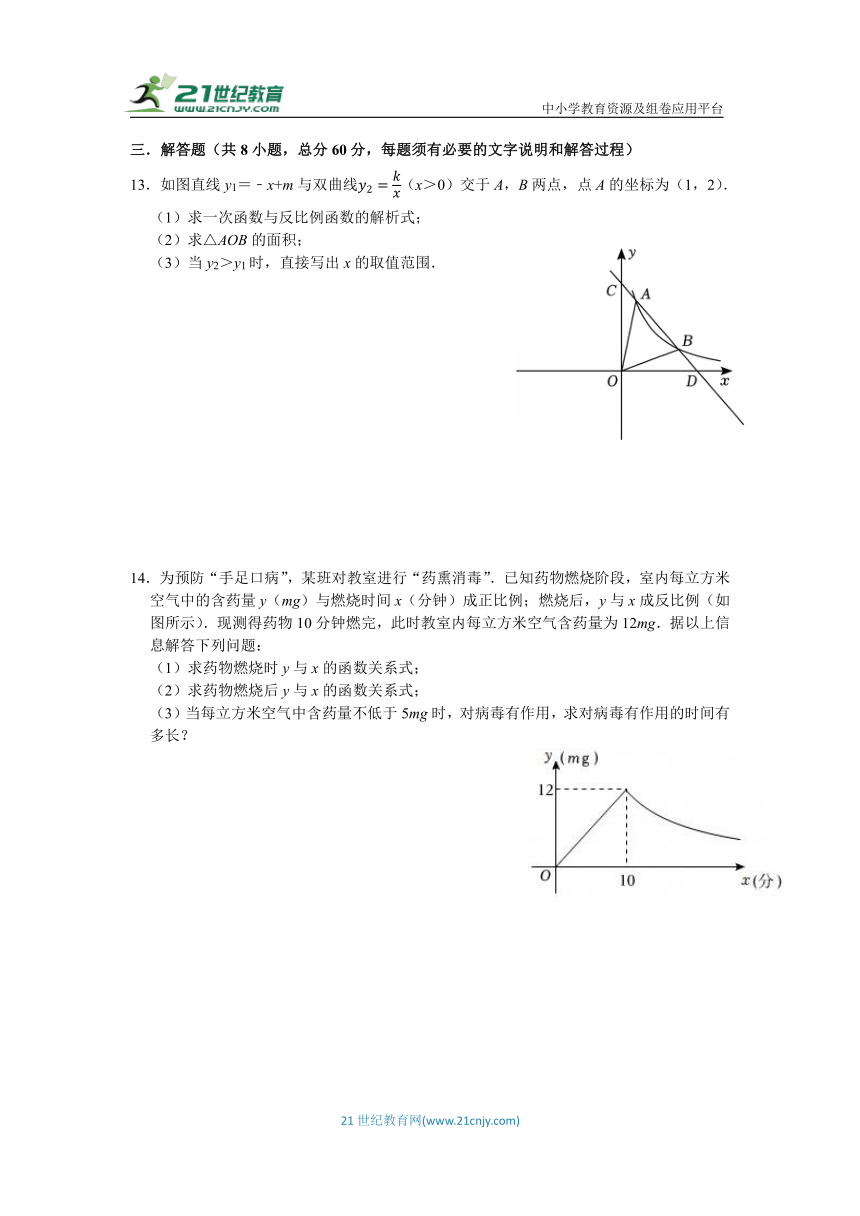
7.如图,矩形ABCD对角线的交点M在x轴上,边AB平行于x轴,OE:OF=1:3,S△BMF=1,反比例函数经过点B,y2经过点D,则k的值是( )
A.2 B.3 C.4 D.5
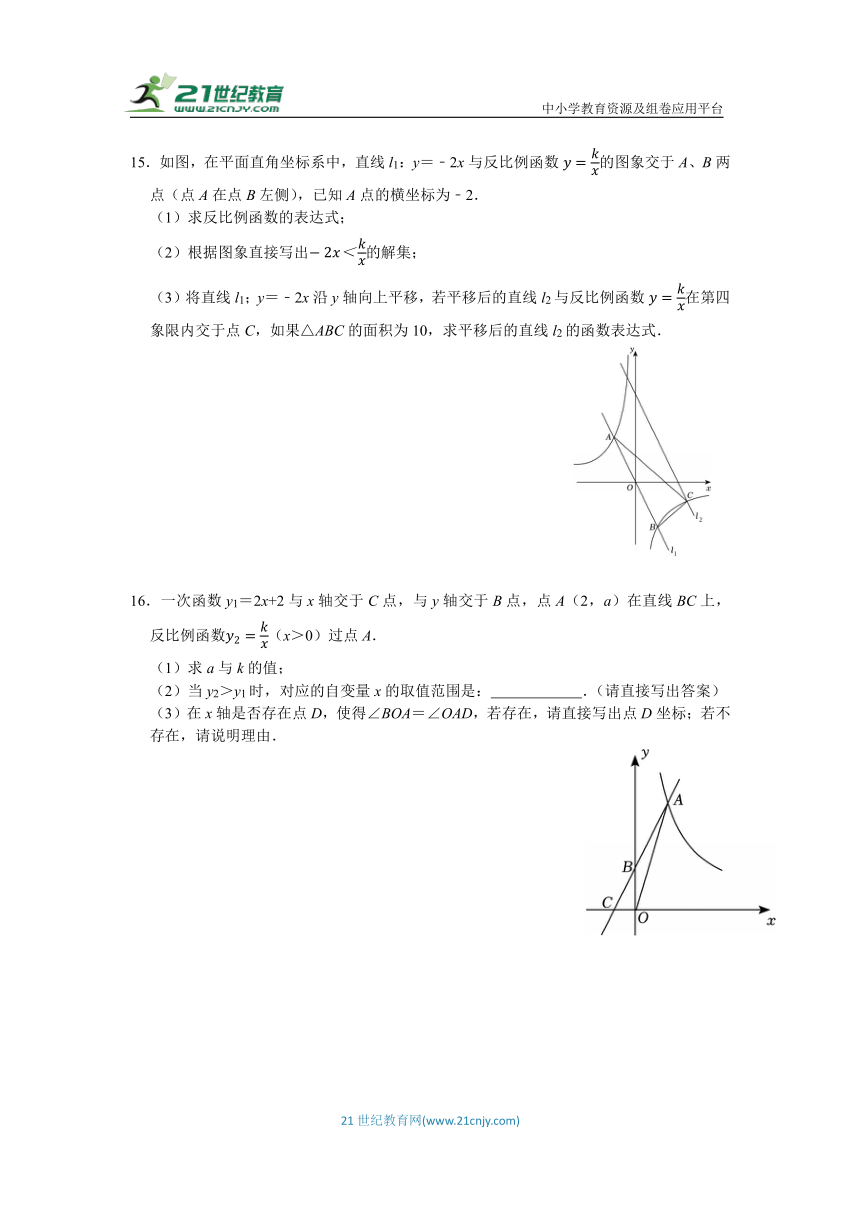
8.如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数y(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点E、F,FD⊥x轴,垂足为D,连接OE、OF、EF,FD与OE相交于点G.下列结论:①OF=OE;②∠EOF=60°;③四边形AEGD与△FOG面积相等;④EF=CF+AE;⑤若∠EOF=45°,EF=4,则直线FE的函数解析式为y=﹣x+4+2.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
二.填空题(每小题5分,满分20分)
9.如图,A为反比例函数图象上一点,AB垂直x轴于B点,若S△AOB=5,则k的值为 .
10.已知反比例函数的图象在每一个象限内,y都随x的增大而减小,则k的取值范围是 .
11.如图,在平面直角坐标系xOy中,直线y=x+4与反比例函数y(k≠0)的图象相交于点AB,若∠AOB=120°,则k的值为 .
12.如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在双曲线上,若点B的横坐标为2,则直线BE的函数解析式为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图直线y1=﹣x+m与双曲线(x>0)交于A,B两点,点A的坐标为(1,2).
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)当y2>y1时,直接写出x的取值范围.
14.为预防“手足口病”,某班对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为12mg.据以上信息解答下列问题:
(1)求药物燃烧时y与x的函数关系式;
(2)求药物燃烧后y与x的函数关系式;
(3)当每立方米空气中含药量不低于5mg时,对病毒有作用,求对病毒有作用的时间有多长?
15.如图,在平面直角坐标系中,直线l1:y=﹣2x与反比例函数的图象交于A、B两点(点A在点B左侧),已知A点的横坐标为﹣2.
(1)求反比例函数的表达式;
(2)根据图象直接写出的解集;
(3)将直线l1;y=﹣2x沿y轴向上平移,若平移后的直线l2与反比例函数在第四象限内交于点C,如果△ABC的面积为10,求平移后的直线l2的函数表达式.
16.一次函数y1=2x+2与x轴交于C点,与y轴交于B点,点A(2,a)在直线BC上,反比例函数(x>0)过点A.
(1)求a与k的值;
(2)当y2>y1时,对应的自变量x的取值范围是: .(请直接写出答案)
(3)在x轴是否存在点D,使得∠BOA=∠OAD,若存在,请直接写出点D坐标;若不存在,请说明理由.
17.如图,一次函数的图象与反比例函数的图象交于点P(a,2),与y轴交于点Q.
(1)求a、k的值;
(2)直线AB过点P,与反比例函数图象交于点A,与x轴交于点B,AP=PB,连接AQ.
①求△APQ的面积;
②点M在反比例函数的图象上,点N在x轴上,若以点M、N、P、Q为顶点的四边形是平行四边形,请求出所有符合条件的点M坐标.
18.在平面直角坐标系中,对于不在坐标轴上的任意点A(x,y),我们把点B()称为点A的“倒数点”.
(1)写出平面直角坐标系中第三象限内“倒数点”是本身的点的坐标 ;
(2)点P(x,y)是反比例函数y(x>0)图象上的一点,点Q(m,n)是点P的“倒数点”,则mn= ;
(3)如图,矩形OCDE的顶点C为(3,0),顶点E在y轴上,函数y(x>0)的图象与DE交于点A.若点B是点A的“倒数点”,且点B在矩形OCDE的一边上,求△OBC的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D D A A C A B B
1.【解答】解:∵反比例函数,
∴图象必经过点(﹣3,2),故选项A正确,不符合题意;
图象位于第二、四象限,故选项B正确,不符合题意;
若x<0,则y>0,故选项C正确,不符合题意;
在每一个象限内,y随x的增大而增大,故选项D不正确,符合题意;
故选:D.
2.【解答】解:∵k=﹣4<0,
∴图象的分支在二、四象限,
∵在第四象限的函数值总小于在第二象限的函数值,
∴y3最小,
∵在同一象限内,y随x的增大而增大,x1<x2<0,
∴y1<y2,
∴y3<y1<y2.
故选:D.
3.【解答】解:如图,
由当﹣4≤x≤﹣1时,﹣4≤y≤﹣1可知反比例函数经过坐标(﹣4,﹣1),
∴,
∴k=4,
∴反比例函数的解析式为,
∴2m=4
∴m=2,
故选:A.
4.【解答】解:解方程组
得,.
因为点A的坐标为(3,2),那么点B的坐标为(﹣3,﹣2).
故选:A.
5.【解答】解:当k>0时,函数y的图象在第一、三象限,函数y=kx+1在第一、二、三象限,故选项C符合题意,选项D不符合题意;
当k<0时,函数y的图象在第二、四象限,函数y=kx+1在第一、二、四象限,故选项A、B不符合题意,
故选:C.
6.【解答】解:∵当R=20,I=11时,
∴电压=20×11=220,
∴.
故选:A.
7.【解答】解:∵OE:OF=1:3,
∴设OE=a,OF=3a,
∴EF=OE+OF=4a,
∵四边形ABCD是矩形,AB∥x轴,
∴BF⊥x轴,AE⊥x轴,
∴∠BFM=∠DEM=90°,
∵矩形ABCD对角线的交点M在x轴上,
∴MB=MD,
在△BFM和△DEM中,
,
∴△BFM≌△DEM(AAS),
∴MF=MEEF=2a,
设BF=b,
∴点B的坐标为(3a,b),
∵S△BMF=1,
∴MF BF=1,
∴2ab=1,
∴ab=1,
∵点B(3a,b)在反比例函数的图象上,
∴k=3ab=3.
故选:B.
8.【解答】解:①S△OCF=S△AOEk,
而OC=OA,故CF=AE,
又∠OCF=∠OAE=90°,
∴△OCF≌△OAE(SAS),
∴OF=OE;
故①正确,符合题意;
②由①知,OF=OE,而EF不一定和OE或OF相等,
即△EFO不一定是等边三角形,故∠EFO不一定等于60°,
故②不一定正确,不符合题意;
③四边形AEGD的面积=S△AEO﹣S△ODGk﹣S△ODG,
△FOG面积=S△ODF﹣S△ODGk﹣S△ODG,
故四边形AEGD与△FOG面积相等,故③正确,符合题意;
④将△OAE绕点O旋转到OCE′时,即CE′=AE,
若∠EOF=45°,则∠EOA+∠FOC=45°,
故∠FOE′=∠E′OC+∠FOC=45°=∠EOF,
而OE=OE′,FO=FO,
∴△FOE′≌△FOE(SAS),
∴EF=E′F=CF+CE′=AE+CF,
即当∠EOF=45°时,才有EF=CF+AE成立,
故④错误,不符合题意;
⑤若∠EOF=45°,由④得EF=CF+AE,由①知CF=AEEF=2,
则BF=BE,故△BEF为等腰直角三角形,
则BE=BFEF=2,
则OA=AB=AE+BE=2+2,
故点E的坐标为(2+2,2),
∵△BEF为等腰直角三角形,故∠BFE=45°,故设直线EF的表达式为:y=﹣x+b,
将点E的坐标代入上式并解得:b=4+2,
故直线FE的函数解析式为y=﹣x+4+2,故⑤正确,符合题意,
故正确的为①③⑤,
故选:B.
二、填空题
9.【解答】解:设A(x,y),则k=xy=±10,
∵图象在二,四象限,
∴k=﹣10.
故答案为:﹣10.
10.【解答】解:∵在每个象限内,y随着x的增大而减小,
∴k﹣1>0,即k>1,
故答案为:k>1.
11.【解答】解:如图,过点O作OE⊥AB于E,过点B作BN⊥y轴于N,
当x=0时,y=0+4=4,
∴点D(0,4),
当y=0时,即x+4=0,
∴x=﹣4,
∴点C(﹣4,0),
∴OC=OD=4,
∴OE=CE=DEOC=2,
由对称性可知OA=OB,
∵∠AOB=120°,
∴∠BOE=60°,
∴OB=2OE=4,
设BN=m,则DN=m,ON=4+m,
在Rt△BON中,由勾股定理得,
BN2+ON2=OB2,
即m2+(m+4)2=(4)2,
解得m=22(m>0),
即BN=DN=22,
∴ON=22+4=22,
∴S△BON(22)(22)|k|,
∴k=8(k>0),
故答案为:8.
12.【解答】解:设正方形ADEF的边长为a,由点B的横坐标为2,
得到正方形OABC的边长为2,即B坐标为(2,2),
则点E的坐标为(a+2,a)(a>0),又点B和E在同一个双曲线上,
∴a(a+2)=4,即(a+1)2=5,解得:a1或a1(舍去),
∴点E坐标为(1,1),
设直线BE的函数解析式为y=kx+b,将点E和B的坐标代入得:
,解得,
∴直线BE的解析式为yx+1.
故答案为:yx+1.
三、解答题
13.【解答】解:(1)把A(1,2)代入y1=﹣x+m得,﹣1+m=2,
∴m=3,
∴一次函数的解析式为y1=﹣x+3,
∵点A在双曲线(x>0)上,
∴k=1×2=2,
∴反比例函数的表达式为y2;
(2)过A作AM⊥x轴于M,过B作BN⊥x轴于N,
∴AM=2,BN=1,MN=1,
∴S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB(2+1)×1;
(3)由题意得,
解得或,
∴A(1,2),B(2,1),
由图象可知:当y2>y1时,x的取值范围是1<x<2.
14.【解答】解:(1)设药物燃烧时的解析式为:y=kx(k≠0),
由题意可得:12=10k,
k,
答:药物燃烧时的解析式为yx(0≤x≤10);
(2)设燃烧后的函数解析式为y(m≠0),
由题意可得:12,
m=120,
答:燃烧后的函数解析式为y(x≥10);
(3)由题意可得:
,
解得:,
24(分钟),
答:对病毒有作用的时间长为分钟.
15.【解答】解:(1)把x=﹣2代入y=﹣2x得,y=4,
∴A(﹣2,4),
把A(﹣2,4)代得k=﹣2×4=﹣8,
∴反比例函数的表达式为y;
(2)解得,,
∴B(2,﹣4),
∴的解集为﹣2<x<0或x>2;
(3)设直线l2与y轴交于D,
设平移后的直线l2的函数表达式为y=﹣2x+b,
∴D(0,b),
连接AD,BD,
∵S△ABD=S△ACB,
∴(2+2)b=10,
∴b=5,
∴平移后的直线l2的函数表达式为y=﹣2x+5.
16.【解答】解:(1)∵点A(2,a)在直线BC上,
∴a=2×2+2=6,
又∵反比例函数(x>0)过点A(2,6),
∴k=12.
(2)当y2>y1时,由图可知0<x<2,
故答案为:0<x<2;
(3)解:当点D在x轴正半轴上时,如图,
过点A作AD1⊥x轴交于点D1,则OB∥AD1,此时∠BOA=∠OAD1,
此时点D1(2,0);
当点D在x轴负半轴上时,如图,设AD2与y轴交于点E(0,n),
∵∠BOA=∠OAD2,
∴OE=AE,
∴(2﹣0)2+(6﹣n)2=n2,
解得,
∴,
设直线AE的解析式为y=mx+b,
则,
解得,
∴直线AE的解析式为,
把y=0代入,得,
∴D2(,0),
综上所述,点D的坐标为(2,0)或.
17.【解答】解:(1)把点P(a,2)代入 得,a=﹣2,
把 P(﹣2,2)代入 得,k=﹣4;
(2)①∵k=﹣4,
∴,
设B的坐标(b,0),点A的坐标为(t,h),
∵AP=PB,P(﹣2,2),
∴h=4,
把A(t,4)代入 得:t=﹣1,
∴点A(﹣1,4),
∵一次函数 的图象与y轴交于点Q.
∴Q的坐标为(0,1),
如图,过点A作AH∥y轴,交PQ于点H,
则点H坐标 ,
∴,
∴;
②设点 ,N(n,0),
∵P(﹣2,2),Q(0,1),点M、N、P、Q构成平行四边形,
当MN和PQ为对角线时,﹣2+1=n+m,2+1=0,
∴,
∴M的坐标为 ,
当MP和NQ为对角线时,m﹣2=n+0,2=0+1,
∴m=4,
∵x<0,
∴m=4(舍去);
当MQ和NP为对角线时,m+0=n﹣2,1=0+2,
∴m=﹣4,
∴M的坐标为 (﹣4,1).
综上所述,点M坐标为 ,(﹣4,1).
18.【解答】解:(1)∵﹣1的倒数是它本身,
∴第三象限内“倒数点”是本身的点的坐标(﹣1,﹣1),
故答案为:(﹣1,﹣1);
(2)∵点P(x,y)是反比例函数y(x>0)图象上的一点,
∴xy,
∵点Q(m,n)是点P的“倒数点”,
∴m,n,
∴mn,
故答案为:;
(3)∵点A在反比例函数y(x>0)的图象上,
∴设点A的坐标为,其中a>0,
∵点B是点A的“倒数点”,
∴点B的坐标为,
∵,
∴点B在反比例函数(x>0)的图象上,
∵反比例函数的图象与坐标轴没有交点,
∴点B不在坐标轴上,
又∵点B在矩形OCDE的一边上,
∴点B只能在ED或CD上,
①当点B在ED上时,点A,B的纵坐标相同,
即,
∴a=2,a=﹣2(不合题意,舍去),
当a=2时,,,
∴点B的坐标为,过点B作BH⊥OC于点H,如图1所示:
∴BH=1,
∵点C(3,0),
∴OC=3
∴S△OBCOC BH3×1;
②当点B在CD上时,点B,C的横坐标相同,
∴,
∴,
当,,,
∴点B的坐标为,如图2所示:
∴BC,
∴S△OBCOC BC.
综上所述:△OBC的面积为或.
21世纪教育网(www.21cnjy.com)
第六章反比例函数单元测试卷浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.已知反比例函数,下列结论中不正确的是( )
A.图象必经过点(﹣3,2)
B.图象位于第二、四象限
C.x<0,则y>0
D.y随x的增大而增大
2.已知(x1,y1),B(x2,y2),C(x3,y3)是反比例函数的图象上的三个点,并且x1<x2<0,x3>0,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y3<y1<y2
3.反比例函数中,当﹣4≤x≤﹣1时,﹣4≤y≤﹣1,点P(2,m)在此反比例函数图象上,则m的值为( )
A.2 B.﹣2 C.8 D.﹣8
4.正比例函数与反比例函数的图象相交于A、B两点,其中点A的坐标为(3,2),那么点B的坐标为( )
A.(﹣3,﹣2) B.(﹣3,2) C.(﹣2,﹣3) D.(2,3)
5.函数y与y=kx+1(k为常数,k≠0)在同一平面直角坐标系中的大致图象是( )
A.B. C.D.
6.电路上在电压保持不变的条件下,电流I(A)与电阻R(Ω)成反比例关系,I与R的函数图象如图,I关于R函数解析式是( )
A. B. C. D.
7.如图,矩形ABCD对角线的交点M在x轴上,边AB平行于x轴,OE:OF=1:3,S△BMF=1,反比例函数经过点B,y2经过点D,则k的值是( )
A.2 B.3 C.4 D.5
8.如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数y(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点E、F,FD⊥x轴,垂足为D,连接OE、OF、EF,FD与OE相交于点G.下列结论:①OF=OE;②∠EOF=60°;③四边形AEGD与△FOG面积相等;④EF=CF+AE;⑤若∠EOF=45°,EF=4,则直线FE的函数解析式为y=﹣x+4+2.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
二.填空题(每小题5分,满分20分)
9.如图,A为反比例函数图象上一点,AB垂直x轴于B点,若S△AOB=5,则k的值为 .
10.已知反比例函数的图象在每一个象限内,y都随x的增大而减小,则k的取值范围是 .
11.如图,在平面直角坐标系xOy中,直线y=x+4与反比例函数y(k≠0)的图象相交于点AB,若∠AOB=120°,则k的值为 .
12.如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在双曲线上,若点B的横坐标为2,则直线BE的函数解析式为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图直线y1=﹣x+m与双曲线(x>0)交于A,B两点,点A的坐标为(1,2).
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积;
(3)当y2>y1时,直接写出x的取值范围.
14.为预防“手足口病”,某班对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为12mg.据以上信息解答下列问题:
(1)求药物燃烧时y与x的函数关系式;
(2)求药物燃烧后y与x的函数关系式;
(3)当每立方米空气中含药量不低于5mg时,对病毒有作用,求对病毒有作用的时间有多长?
15.如图,在平面直角坐标系中,直线l1:y=﹣2x与反比例函数的图象交于A、B两点(点A在点B左侧),已知A点的横坐标为﹣2.
(1)求反比例函数的表达式;
(2)根据图象直接写出的解集;
(3)将直线l1;y=﹣2x沿y轴向上平移,若平移后的直线l2与反比例函数在第四象限内交于点C,如果△ABC的面积为10,求平移后的直线l2的函数表达式.
16.一次函数y1=2x+2与x轴交于C点,与y轴交于B点,点A(2,a)在直线BC上,反比例函数(x>0)过点A.
(1)求a与k的值;
(2)当y2>y1时,对应的自变量x的取值范围是: .(请直接写出答案)
(3)在x轴是否存在点D,使得∠BOA=∠OAD,若存在,请直接写出点D坐标;若不存在,请说明理由.
17.如图,一次函数的图象与反比例函数的图象交于点P(a,2),与y轴交于点Q.
(1)求a、k的值;
(2)直线AB过点P,与反比例函数图象交于点A,与x轴交于点B,AP=PB,连接AQ.
①求△APQ的面积;
②点M在反比例函数的图象上,点N在x轴上,若以点M、N、P、Q为顶点的四边形是平行四边形,请求出所有符合条件的点M坐标.
18.在平面直角坐标系中,对于不在坐标轴上的任意点A(x,y),我们把点B()称为点A的“倒数点”.
(1)写出平面直角坐标系中第三象限内“倒数点”是本身的点的坐标 ;
(2)点P(x,y)是反比例函数y(x>0)图象上的一点,点Q(m,n)是点P的“倒数点”,则mn= ;
(3)如图,矩形OCDE的顶点C为(3,0),顶点E在y轴上,函数y(x>0)的图象与DE交于点A.若点B是点A的“倒数点”,且点B在矩形OCDE的一边上,求△OBC的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D D A A C A B B
1.【解答】解:∵反比例函数,
∴图象必经过点(﹣3,2),故选项A正确,不符合题意;
图象位于第二、四象限,故选项B正确,不符合题意;
若x<0,则y>0,故选项C正确,不符合题意;
在每一个象限内,y随x的增大而增大,故选项D不正确,符合题意;
故选:D.
2.【解答】解:∵k=﹣4<0,
∴图象的分支在二、四象限,
∵在第四象限的函数值总小于在第二象限的函数值,
∴y3最小,
∵在同一象限内,y随x的增大而增大,x1<x2<0,
∴y1<y2,
∴y3<y1<y2.
故选:D.
3.【解答】解:如图,
由当﹣4≤x≤﹣1时,﹣4≤y≤﹣1可知反比例函数经过坐标(﹣4,﹣1),
∴,
∴k=4,
∴反比例函数的解析式为,
∴2m=4
∴m=2,
故选:A.
4.【解答】解:解方程组
得,.
因为点A的坐标为(3,2),那么点B的坐标为(﹣3,﹣2).
故选:A.
5.【解答】解:当k>0时,函数y的图象在第一、三象限,函数y=kx+1在第一、二、三象限,故选项C符合题意,选项D不符合题意;
当k<0时,函数y的图象在第二、四象限,函数y=kx+1在第一、二、四象限,故选项A、B不符合题意,
故选:C.
6.【解答】解:∵当R=20,I=11时,
∴电压=20×11=220,
∴.
故选:A.
7.【解答】解:∵OE:OF=1:3,
∴设OE=a,OF=3a,
∴EF=OE+OF=4a,
∵四边形ABCD是矩形,AB∥x轴,
∴BF⊥x轴,AE⊥x轴,
∴∠BFM=∠DEM=90°,
∵矩形ABCD对角线的交点M在x轴上,
∴MB=MD,
在△BFM和△DEM中,
,
∴△BFM≌△DEM(AAS),
∴MF=MEEF=2a,
设BF=b,
∴点B的坐标为(3a,b),
∵S△BMF=1,
∴MF BF=1,
∴2ab=1,
∴ab=1,
∵点B(3a,b)在反比例函数的图象上,
∴k=3ab=3.
故选:B.
8.【解答】解:①S△OCF=S△AOEk,
而OC=OA,故CF=AE,
又∠OCF=∠OAE=90°,
∴△OCF≌△OAE(SAS),
∴OF=OE;
故①正确,符合题意;
②由①知,OF=OE,而EF不一定和OE或OF相等,
即△EFO不一定是等边三角形,故∠EFO不一定等于60°,
故②不一定正确,不符合题意;
③四边形AEGD的面积=S△AEO﹣S△ODGk﹣S△ODG,
△FOG面积=S△ODF﹣S△ODGk﹣S△ODG,
故四边形AEGD与△FOG面积相等,故③正确,符合题意;
④将△OAE绕点O旋转到OCE′时,即CE′=AE,
若∠EOF=45°,则∠EOA+∠FOC=45°,
故∠FOE′=∠E′OC+∠FOC=45°=∠EOF,
而OE=OE′,FO=FO,
∴△FOE′≌△FOE(SAS),
∴EF=E′F=CF+CE′=AE+CF,
即当∠EOF=45°时,才有EF=CF+AE成立,
故④错误,不符合题意;
⑤若∠EOF=45°,由④得EF=CF+AE,由①知CF=AEEF=2,
则BF=BE,故△BEF为等腰直角三角形,
则BE=BFEF=2,
则OA=AB=AE+BE=2+2,
故点E的坐标为(2+2,2),
∵△BEF为等腰直角三角形,故∠BFE=45°,故设直线EF的表达式为:y=﹣x+b,
将点E的坐标代入上式并解得:b=4+2,
故直线FE的函数解析式为y=﹣x+4+2,故⑤正确,符合题意,
故正确的为①③⑤,
故选:B.
二、填空题
9.【解答】解:设A(x,y),则k=xy=±10,
∵图象在二,四象限,
∴k=﹣10.
故答案为:﹣10.
10.【解答】解:∵在每个象限内,y随着x的增大而减小,
∴k﹣1>0,即k>1,
故答案为:k>1.
11.【解答】解:如图,过点O作OE⊥AB于E,过点B作BN⊥y轴于N,
当x=0时,y=0+4=4,
∴点D(0,4),
当y=0时,即x+4=0,
∴x=﹣4,
∴点C(﹣4,0),
∴OC=OD=4,
∴OE=CE=DEOC=2,
由对称性可知OA=OB,
∵∠AOB=120°,
∴∠BOE=60°,
∴OB=2OE=4,
设BN=m,则DN=m,ON=4+m,
在Rt△BON中,由勾股定理得,
BN2+ON2=OB2,
即m2+(m+4)2=(4)2,
解得m=22(m>0),
即BN=DN=22,
∴ON=22+4=22,
∴S△BON(22)(22)|k|,
∴k=8(k>0),
故答案为:8.
12.【解答】解:设正方形ADEF的边长为a,由点B的横坐标为2,
得到正方形OABC的边长为2,即B坐标为(2,2),
则点E的坐标为(a+2,a)(a>0),又点B和E在同一个双曲线上,
∴a(a+2)=4,即(a+1)2=5,解得:a1或a1(舍去),
∴点E坐标为(1,1),
设直线BE的函数解析式为y=kx+b,将点E和B的坐标代入得:
,解得,
∴直线BE的解析式为yx+1.
故答案为:yx+1.
三、解答题
13.【解答】解:(1)把A(1,2)代入y1=﹣x+m得,﹣1+m=2,
∴m=3,
∴一次函数的解析式为y1=﹣x+3,
∵点A在双曲线(x>0)上,
∴k=1×2=2,
∴反比例函数的表达式为y2;
(2)过A作AM⊥x轴于M,过B作BN⊥x轴于N,
∴AM=2,BN=1,MN=1,
∴S△AOB=S△AOM+S梯形AMNB﹣S△BON=S梯形AMNB(2+1)×1;
(3)由题意得,
解得或,
∴A(1,2),B(2,1),
由图象可知:当y2>y1时,x的取值范围是1<x<2.
14.【解答】解:(1)设药物燃烧时的解析式为:y=kx(k≠0),
由题意可得:12=10k,
k,
答:药物燃烧时的解析式为yx(0≤x≤10);
(2)设燃烧后的函数解析式为y(m≠0),
由题意可得:12,
m=120,
答:燃烧后的函数解析式为y(x≥10);
(3)由题意可得:
,
解得:,
24(分钟),
答:对病毒有作用的时间长为分钟.
15.【解答】解:(1)把x=﹣2代入y=﹣2x得,y=4,
∴A(﹣2,4),
把A(﹣2,4)代得k=﹣2×4=﹣8,
∴反比例函数的表达式为y;
(2)解得,,
∴B(2,﹣4),
∴的解集为﹣2<x<0或x>2;
(3)设直线l2与y轴交于D,
设平移后的直线l2的函数表达式为y=﹣2x+b,
∴D(0,b),
连接AD,BD,
∵S△ABD=S△ACB,
∴(2+2)b=10,
∴b=5,
∴平移后的直线l2的函数表达式为y=﹣2x+5.
16.【解答】解:(1)∵点A(2,a)在直线BC上,
∴a=2×2+2=6,
又∵反比例函数(x>0)过点A(2,6),
∴k=12.
(2)当y2>y1时,由图可知0<x<2,
故答案为:0<x<2;
(3)解:当点D在x轴正半轴上时,如图,
过点A作AD1⊥x轴交于点D1,则OB∥AD1,此时∠BOA=∠OAD1,
此时点D1(2,0);
当点D在x轴负半轴上时,如图,设AD2与y轴交于点E(0,n),
∵∠BOA=∠OAD2,
∴OE=AE,
∴(2﹣0)2+(6﹣n)2=n2,
解得,
∴,
设直线AE的解析式为y=mx+b,
则,
解得,
∴直线AE的解析式为,
把y=0代入,得,
∴D2(,0),
综上所述,点D的坐标为(2,0)或.
17.【解答】解:(1)把点P(a,2)代入 得,a=﹣2,
把 P(﹣2,2)代入 得,k=﹣4;
(2)①∵k=﹣4,
∴,
设B的坐标(b,0),点A的坐标为(t,h),
∵AP=PB,P(﹣2,2),
∴h=4,
把A(t,4)代入 得:t=﹣1,
∴点A(﹣1,4),
∵一次函数 的图象与y轴交于点Q.
∴Q的坐标为(0,1),
如图,过点A作AH∥y轴,交PQ于点H,
则点H坐标 ,
∴,
∴;
②设点 ,N(n,0),
∵P(﹣2,2),Q(0,1),点M、N、P、Q构成平行四边形,
当MN和PQ为对角线时,﹣2+1=n+m,2+1=0,
∴,
∴M的坐标为 ,
当MP和NQ为对角线时,m﹣2=n+0,2=0+1,
∴m=4,
∵x<0,
∴m=4(舍去);
当MQ和NP为对角线时,m+0=n﹣2,1=0+2,
∴m=﹣4,
∴M的坐标为 (﹣4,1).
综上所述,点M坐标为 ,(﹣4,1).
18.【解答】解:(1)∵﹣1的倒数是它本身,
∴第三象限内“倒数点”是本身的点的坐标(﹣1,﹣1),
故答案为:(﹣1,﹣1);
(2)∵点P(x,y)是反比例函数y(x>0)图象上的一点,
∴xy,
∵点Q(m,n)是点P的“倒数点”,
∴m,n,
∴mn,
故答案为:;
(3)∵点A在反比例函数y(x>0)的图象上,
∴设点A的坐标为,其中a>0,
∵点B是点A的“倒数点”,
∴点B的坐标为,
∵,
∴点B在反比例函数(x>0)的图象上,
∵反比例函数的图象与坐标轴没有交点,
∴点B不在坐标轴上,
又∵点B在矩形OCDE的一边上,
∴点B只能在ED或CD上,
①当点B在ED上时,点A,B的纵坐标相同,
即,
∴a=2,a=﹣2(不合题意,舍去),
当a=2时,,,
∴点B的坐标为,过点B作BH⊥OC于点H,如图1所示:
∴BH=1,
∵点C(3,0),
∴OC=3
∴S△OBCOC BH3×1;
②当点B在CD上时,点B,C的横坐标相同,
∴,
∴,
当,,,
∴点B的坐标为,如图2所示:
∴BC,
∴S△OBCOC BC.
综上所述:△OBC的面积为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
