第四章平行四边形单元测试卷(含解析)
文档属性
| 名称 | 第四章平行四边形单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 687.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-25 21:03:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章平行四边形单元测试卷浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列四幅图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
3.现有正三角形、正方形、正六边形、正八边形地砖,若只能选择一种地砖铺设地面,则可供选择的地砖有( )
A.1种 B.2种 C.3种 D.4种
4.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=3,AE=2,则DE的长为( )
A. B. C.5 D.6
5.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D B.AB=AD,CB=CD
C.AB=CD,AD=BC D.AB∥CD,AD=BC
6.玲玲在用反证法证明“△ABC中至少有一个内角小于或等于60°”时,她应先假设这个三角形中( )
A.有一个内角大于60° B.有一个内角大于等于60°
C.每一个内角都大于60° D.每一个内角都小于60°
7.如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=2,则四边形EFCD的周长为( )
A.12 B.13 C.24 D.28
8.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30 C.40 D.50
二.填空题(每小题5分,满分20分)
9.如图A,B两处被池塘阻隔,为测量A,B两地的距离,在地面上选一点C,连结CA,CB,分别取CA,CB的中点D,E.测得DE=5m,则A,B两地的距离为 m.
10.如图,在△ABC中,∠A=50°,剪去∠A成四边形,则∠1+∠2的度数为 .
11.如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(﹣5,2),(﹣2,﹣2),(5,﹣2),则点D的坐标为 .
12.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知正x边形的内角和为1080°,边长为2.
(1)求正x边形的周长;
(2)若正n边形的每个外角的度数比正x边形每个内角的度数小63°,求n的值.
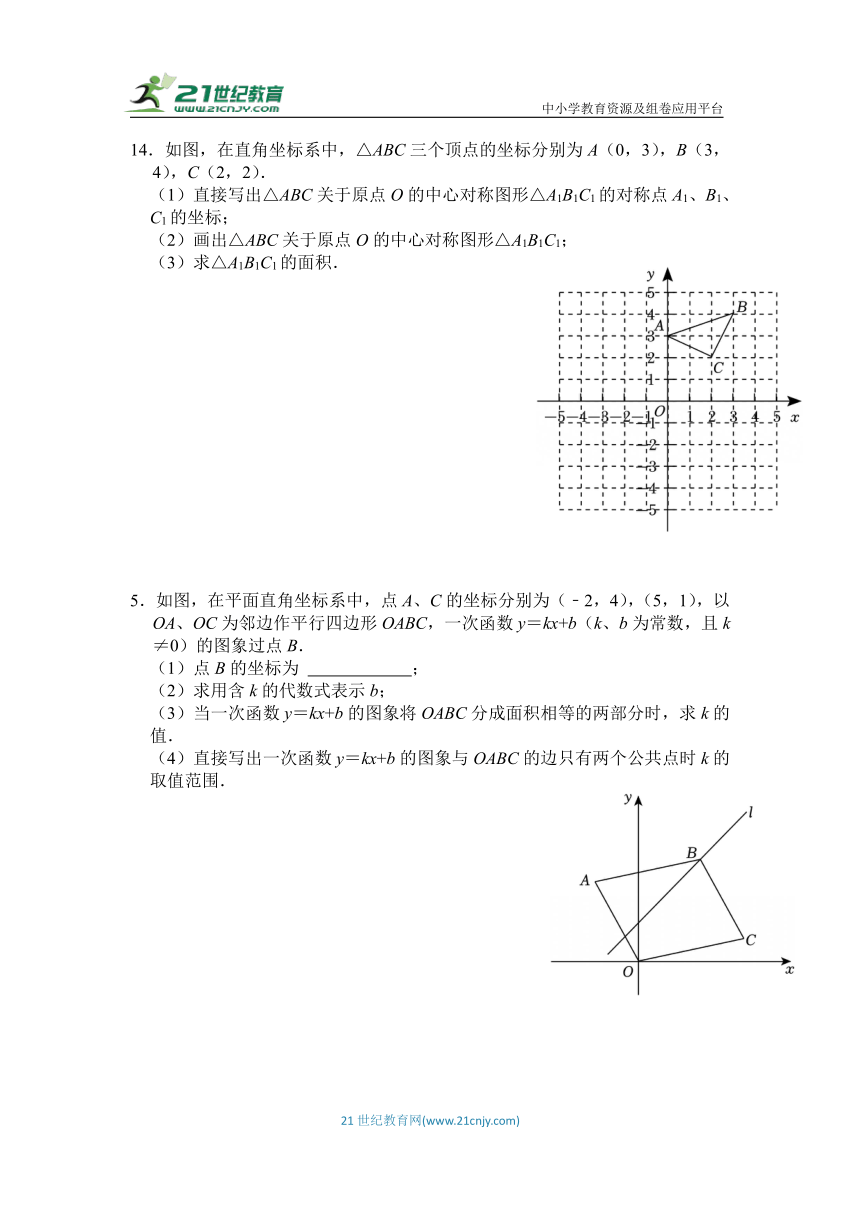
14.如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).
(1)直接写出△ABC关于原点O的中心对称图形△A1B1C1的对称点A1、B1、C1的坐标;
(2)画出△ABC关于原点O的中心对称图形△A1B1C1;
(3)求△A1B1C1的面积.
5.如图,在平面直角坐标系中,点A、C的坐标分别为(﹣2,4),(5,1),以OA、OC为邻边作平行四边形OABC,一次函数y=kx+b(k、b为常数,且k≠0)的图象过点B.
(1)点B的坐标为 ;
(2)求用含k的代数式表示b;
(3)当一次函数y=kx+b的图象将OABC分成面积相等的两部分时,求k的值.
(4)直接写出一次函数y=kx+b的图象与OABC的边只有两个公共点时k的取值范围.
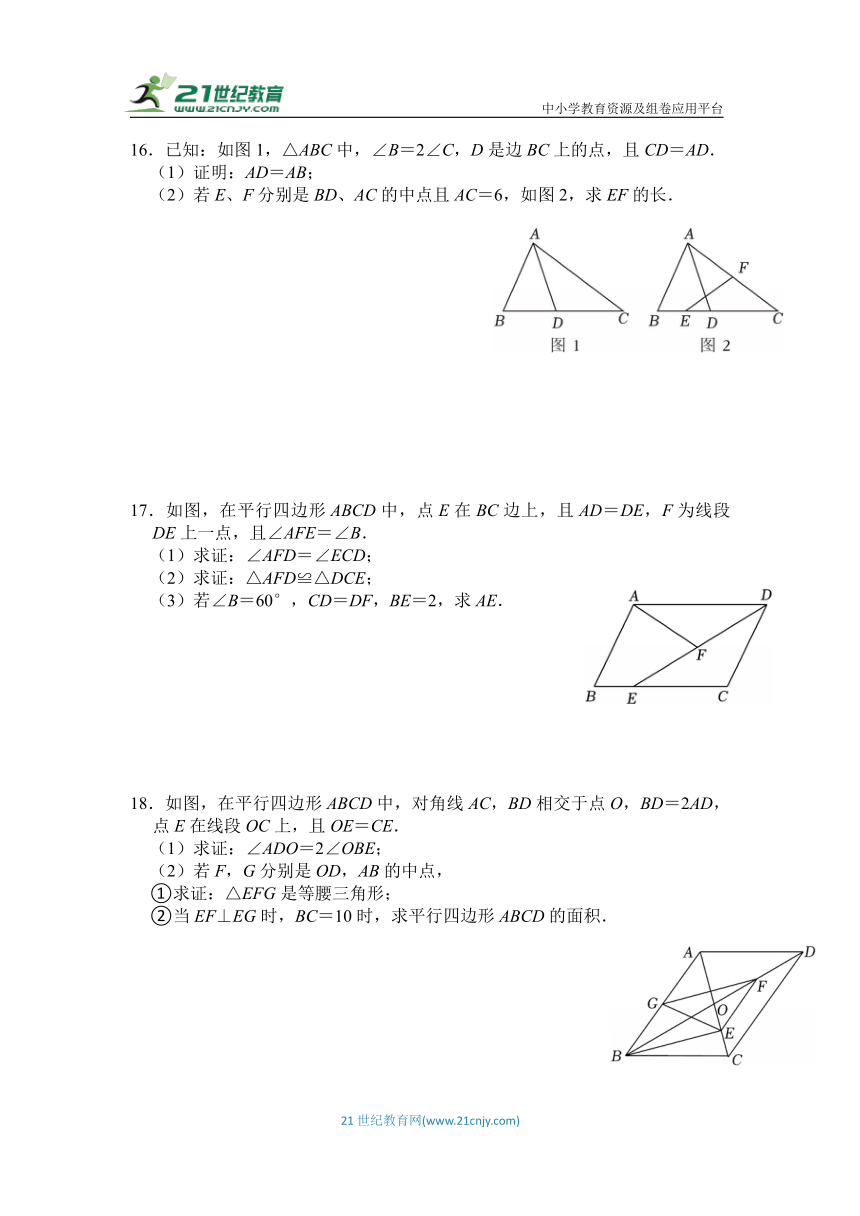
16.已知:如图1,△ABC中,∠B=2∠C,D是边BC上的点,且CD=AD.
(1)证明:AD=AB;
(2)若E、F分别是BD、AC的中点且AC=6,如图2,求EF的长.
17.如图,在平行四边形ABCD中,点E在BC边上,且AD=DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠AFD=∠ECD;
(2)求证:△AFD≌△DCE;
(3)若∠B=60°,CD=DF,BE=2,求AE.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠ADO=2∠OBE;
(2)若F,G分别是OD,AB的中点,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,BC=10时,求平行四边形ABCD的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 B D C B C C B B
1.【解答】解:A.是轴对称图形,不是中心对称图形,不符合题意.
B.既是轴对称图形,又是中心对称图形,符合题意.
C.是轴对称图形,不是中心对称图形,不符合题意.
D.是轴对称图形,不是中心对称图形,不符合题意.
故选:B.
2.【解答】解:根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成n﹣2个三角形,
∴n﹣2=7,即n=9.
故选:D.
3.【解答】解:①正三角形的每个内角是60°,能整除360°,能够铺满地面;
②正方形的每个内角是90°,能整除360°,能够铺满地面;
③正六边形的每个内角是120°,能整除360°,能够铺满地面;
④正八边形的每个内角为:180°﹣360°÷8=135°,不能整除360°,不能够铺满地面.
故选:C.
4.【解答】解:平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,AB=3,
∴AB∥CD,AB=CD=3,AD=BC,AD∥BC,
∴∠BAD+∠CDA=180°,∠DAE=∠AEB,∠ADE=∠CED,
∴,,
∴,∠BAE=∠AEB,∠DEC=∠CDE,
∴AB=BE=3,CD=EC=3,
∴BC=BE+CE=3+3=6=AD,
∵AE=2,
∴.
故选:B.
5.【解答】解:A、由∠A=∠B,∠C=∠D,不能判定四边形ABCD是平行四边形,故选项A不符合题意;
B、由AB=AD,CB=CD,不能四边形ABCD是平行四边形,故选项B不符合题意;
C、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故选项C符合题意;
D、由AB∥CD,AD=BC,不能四边形ABCD是平行四边形,故选项D不符合题意;
故选:C.
6.【解答】解:用反证法证明“△ABC中至少有一个内角小于或等于60°”时,应先假设这个三角形中每一个内角都大于60°,
故选:C.
7.【解答】解:EF过 ABCD对角线的交点O,交AD于E,交BC于F,
由题意可得:AD∥BC,AD=BC,AO=CO,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴AE=CF,EO=FO=2,
∵C四边形ABCD=18,
∴CD+AD=9,
∴C四边形CDEF=CD+DE+EF+FC=CD+DE+2OE+AE=CD+AD+2OE=9+4=13.
故选:B.
8.【解答】解:如图,连接MN,过点A作AF⊥BC于F,
∵AB=AC,BC=10cm,
∴BFBC=5cm,
由勾股定理得:AF12(cm),
∵M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,
∴MNBC=5cm,MN∥BC,
∴图中阴影部分可以看作三个以5cm为底,且高的和为12cm的三角形,
∴S阴影部分5×12=30(cm2),
故选:B.
二、填空题
9.【解答】解:∵分别取CA,CB的中点D,E.测得DE=5m,
∴DE是三角形ABC的中位线,
∴AB=2DE=10m,
故答案为:10.
10.【解答】解:∵在△ABC中,∠A=50°,
∴∠B+∠C=180°﹣50°=130°,
由四边形内角和是360°,则∠1+∠2=360°﹣(∠B+∠C)=360°﹣130°=230°,
故答案为:230°.
11.【解答】解:∵点A,C的坐标分别为(﹣5,2),(5,﹣2),
∴点O是AC的中点,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴BD经过点O,
∵B的坐标为(﹣2,﹣2),
∴D的坐标为(2,2),
故答案为:(2,2).
12.【解答】解:如图所示,
由三角形外角的性质可得,∠1=∠A+∠G,
由四边形的内角和是360°可得,
∠1+∠2+∠E+∠F=360°,∠3+∠B+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G
=∠1+∠C+∠D+∠E+∠F+∠B
=360°×2﹣180°
=540°.
故答案为:540°.
三、解答题
13.【解答】解:(1)由题意可得180×(x﹣2)=1080,
解得x=8.
正x边形的周长为8×2=16;
(2)正x边形每个内角的度数为1080°÷8=135°,
正n边形的每个外角的度数为135°﹣63°=72°,
360°÷72°=5,
∴n的值为5.
14.【解答】解:(1)∵A(0,3),B(3,4),C(2,2),
∴A1(0,﹣3),B1(﹣3,﹣4),C1(﹣2,﹣2);
(2)如图,△A1B1C1即为所求,
(3)△A1B1C1的面积为.
15.【解答】解:(1)∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,
∴AB可由OC平移得到,
∵点A(﹣2,4),点C(5,1),O(0,0),
∴B(5﹣2,1+4),
即B(3,5),
故答案为:(3,5);
(2)将B(3,5)代入y=kx+b,得:3k+b=5,
∴b=5﹣3k;
(3)一次函数y=kx+b(k、b为常数,且k≠0)的图象过点B,
∴当一次函数y=kx+b的图象将平行四边形OABC分成面积相等的两部分时,图象必过(0,0)点,
由(2)知:y=kx+5﹣3k,
∴5﹣3k=0,
∴;
(4)当直线y=kx+b经过A点时,得,
解得:,
当直线y=kx+b经过C点时,得,
解得:k=﹣2,
∵一次函数y=kx+b的图象与平行四边形OABC的边只有两个公共点,
∴或k<﹣2.
16.【解答】(1)证明:∵CD=AD,
∴∠C=∠DAC,
∴∠ADB=∠C+∠DAC=2∠C;
∵∠B=2∠C,
∴∠ADB=∠B,
∴AD=AB;
(2)解:如图,连接AE,
由(1)知,AD=AB,
又∵E是BD的中点,
∴AE⊥BD,
∴△AEC是直角三角形,
∵F是AC的中点,AC=6,
∴.
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠B+∠ECD=180°,
∵∠AFE=∠B,
∴∠AFE+∠ECD=180°,
又∵∠AFE+∠AFD=180°,
∴∠AFD=∠ECD;
(2)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC,
在△AFD和△DCE中,
,
∴△AFD≌△DCE(AAS),
(3)解:过点E作EH⊥AB于H,如图所示:
由(2)可知:△AFD≌△DCE,
∴DF=CE,AF=CD,
∵四边形ABCD为平行四边形,
∴BC=AD,AB=CD,
∵AD=DE,
∴BC=DE,
∵DE=DF+EF=CE+EF,BC=CE+BE,
∴BE=EF,
∵AB=CD,CD=DF,AF=CD,DF=CE,
∴AB=AF=CD=CE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SSS),
∴∠AEB=∠AEF,
∴∠B=60°,
∴∠C=180°﹣∠B=120°,
∵CD=CE,
∴∠CED=∠CDE(180°﹣∠C)=30°,
∴∠BEF=180°﹣∠CED=150°,
∴∠AEB=∠AEF∠BEF=75°,
∵EH⊥AB,∠B=60°,
∴∠BEH=30°,
∴∠AEH=∠AEB﹣∠BEH=45°,
∴△AHE为等腰直角三角形,即HE=HA,
在Rt△BEH中,∠∠BEH=30°,BE=2,
∴BHBE=1,
由勾股定理得:HE,
∴HE=HA,
∴AE.
18.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,BD=2DO=2BO,
∴∠ADO=∠CBO,
∵BD=2AD,
∴AD=BO=BC,
∴△BOC是等腰三角形,
∵OE=CE,
∴∠OBE=∠CBE∠ADO,
∴∠ADO=2∠OBE.
(2)①证明:∵△BOC是等腰三角形,E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EGAB,
∵E、F分别是OC、OD的中点,
∴EFCD,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴EG=EF,
∴△EFG是等腰三角形.
②解:由题意知,EF∥CD∥BG,
∴EFAB=BG,
∴四边形BEFG是平行四边形,
∴∠EFG=∠GBE,
∵∠FEG=∠AEB=90°,
∴△EFG∽△EBA,
∴△ABE是等腰三角形,
∴∠BAE=∠ABE=45°,
∴EG⊥AB,
设AG=GE=x,则BE=AEx,CE,
在Rt△BCE中,由勾股定理得,BC2=BE2+CE2,即,
解得x=3或x=﹣3(不合题意,舍去),
∴BE=3,AC=4CE=4,
∴S平行四边形ABCD=2120,
∴平行四边形ABCD的面积为120.
21世纪教育网(www.21cnjy.com)
第四章平行四边形单元测试卷浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列四幅图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.过某个多边形的一个顶点的所有对角线,将这个多边形分成7个三角形,则这个多边形是( )
A.六边形 B.七边形 C.八边形 D.九边形
3.现有正三角形、正方形、正六边形、正八边形地砖,若只能选择一种地砖铺设地面,则可供选择的地砖有( )
A.1种 B.2种 C.3种 D.4种
4.如图,在平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,若AB=3,AE=2,则DE的长为( )
A. B. C.5 D.6
5.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠B,∠C=∠D B.AB=AD,CB=CD
C.AB=CD,AD=BC D.AB∥CD,AD=BC
6.玲玲在用反证法证明“△ABC中至少有一个内角小于或等于60°”时,她应先假设这个三角形中( )
A.有一个内角大于60° B.有一个内角大于等于60°
C.每一个内角都大于60° D.每一个内角都小于60°
7.如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=2,则四边形EFCD的周长为( )
A.12 B.13 C.24 D.28
8.如图,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连结DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为( )cm2.
A.20 B.30 C.40 D.50
二.填空题(每小题5分,满分20分)
9.如图A,B两处被池塘阻隔,为测量A,B两地的距离,在地面上选一点C,连结CA,CB,分别取CA,CB的中点D,E.测得DE=5m,则A,B两地的距离为 m.
10.如图,在△ABC中,∠A=50°,剪去∠A成四边形,则∠1+∠2的度数为 .
11.如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(﹣5,2),(﹣2,﹣2),(5,﹣2),则点D的坐标为 .
12.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知正x边形的内角和为1080°,边长为2.
(1)求正x边形的周长;
(2)若正n边形的每个外角的度数比正x边形每个内角的度数小63°,求n的值.
14.如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).
(1)直接写出△ABC关于原点O的中心对称图形△A1B1C1的对称点A1、B1、C1的坐标;
(2)画出△ABC关于原点O的中心对称图形△A1B1C1;
(3)求△A1B1C1的面积.
5.如图,在平面直角坐标系中,点A、C的坐标分别为(﹣2,4),(5,1),以OA、OC为邻边作平行四边形OABC,一次函数y=kx+b(k、b为常数,且k≠0)的图象过点B.
(1)点B的坐标为 ;
(2)求用含k的代数式表示b;
(3)当一次函数y=kx+b的图象将OABC分成面积相等的两部分时,求k的值.
(4)直接写出一次函数y=kx+b的图象与OABC的边只有两个公共点时k的取值范围.
16.已知:如图1,△ABC中,∠B=2∠C,D是边BC上的点,且CD=AD.
(1)证明:AD=AB;
(2)若E、F分别是BD、AC的中点且AC=6,如图2,求EF的长.
17.如图,在平行四边形ABCD中,点E在BC边上,且AD=DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:∠AFD=∠ECD;
(2)求证:△AFD≌△DCE;
(3)若∠B=60°,CD=DF,BE=2,求AE.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠ADO=2∠OBE;
(2)若F,G分别是OD,AB的中点,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,BC=10时,求平行四边形ABCD的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 B D C B C C B B
1.【解答】解:A.是轴对称图形,不是中心对称图形,不符合题意.
B.既是轴对称图形,又是中心对称图形,符合题意.
C.是轴对称图形,不是中心对称图形,不符合题意.
D.是轴对称图形,不是中心对称图形,不符合题意.
故选:B.
2.【解答】解:根据n边形从一个顶点出发可引出(n﹣3)条对角线,可组成n﹣2个三角形,
∴n﹣2=7,即n=9.
故选:D.
3.【解答】解:①正三角形的每个内角是60°,能整除360°,能够铺满地面;
②正方形的每个内角是90°,能整除360°,能够铺满地面;
③正六边形的每个内角是120°,能整除360°,能够铺满地面;
④正八边形的每个内角为:180°﹣360°÷8=135°,不能整除360°,不能够铺满地面.
故选:C.
4.【解答】解:平行四边形ABCD中,∠BAD的平分线和∠CDA的平分线交于BC上一点E,AB=3,
∴AB∥CD,AB=CD=3,AD=BC,AD∥BC,
∴∠BAD+∠CDA=180°,∠DAE=∠AEB,∠ADE=∠CED,
∴,,
∴,∠BAE=∠AEB,∠DEC=∠CDE,
∴AB=BE=3,CD=EC=3,
∴BC=BE+CE=3+3=6=AD,
∵AE=2,
∴.
故选:B.
5.【解答】解:A、由∠A=∠B,∠C=∠D,不能判定四边形ABCD是平行四边形,故选项A不符合题意;
B、由AB=AD,CB=CD,不能四边形ABCD是平行四边形,故选项B不符合题意;
C、∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,故选项C符合题意;
D、由AB∥CD,AD=BC,不能四边形ABCD是平行四边形,故选项D不符合题意;
故选:C.
6.【解答】解:用反证法证明“△ABC中至少有一个内角小于或等于60°”时,应先假设这个三角形中每一个内角都大于60°,
故选:C.
7.【解答】解:EF过 ABCD对角线的交点O,交AD于E,交BC于F,
由题意可得:AD∥BC,AD=BC,AO=CO,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴AE=CF,EO=FO=2,
∵C四边形ABCD=18,
∴CD+AD=9,
∴C四边形CDEF=CD+DE+EF+FC=CD+DE+2OE+AE=CD+AD+2OE=9+4=13.
故选:B.
8.【解答】解:如图,连接MN,过点A作AF⊥BC于F,
∵AB=AC,BC=10cm,
∴BFBC=5cm,
由勾股定理得:AF12(cm),
∵M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,
∴MNBC=5cm,MN∥BC,
∴图中阴影部分可以看作三个以5cm为底,且高的和为12cm的三角形,
∴S阴影部分5×12=30(cm2),
故选:B.
二、填空题
9.【解答】解:∵分别取CA,CB的中点D,E.测得DE=5m,
∴DE是三角形ABC的中位线,
∴AB=2DE=10m,
故答案为:10.
10.【解答】解:∵在△ABC中,∠A=50°,
∴∠B+∠C=180°﹣50°=130°,
由四边形内角和是360°,则∠1+∠2=360°﹣(∠B+∠C)=360°﹣130°=230°,
故答案为:230°.
11.【解答】解:∵点A,C的坐标分别为(﹣5,2),(5,﹣2),
∴点O是AC的中点,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴BD经过点O,
∵B的坐标为(﹣2,﹣2),
∴D的坐标为(2,2),
故答案为:(2,2).
12.【解答】解:如图所示,
由三角形外角的性质可得,∠1=∠A+∠G,
由四边形的内角和是360°可得,
∠1+∠2+∠E+∠F=360°,∠3+∠B+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G
=∠1+∠C+∠D+∠E+∠F+∠B
=360°×2﹣180°
=540°.
故答案为:540°.
三、解答题
13.【解答】解:(1)由题意可得180×(x﹣2)=1080,
解得x=8.
正x边形的周长为8×2=16;
(2)正x边形每个内角的度数为1080°÷8=135°,
正n边形的每个外角的度数为135°﹣63°=72°,
360°÷72°=5,
∴n的值为5.
14.【解答】解:(1)∵A(0,3),B(3,4),C(2,2),
∴A1(0,﹣3),B1(﹣3,﹣4),C1(﹣2,﹣2);
(2)如图,△A1B1C1即为所求,
(3)△A1B1C1的面积为.
15.【解答】解:(1)∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,
∴AB可由OC平移得到,
∵点A(﹣2,4),点C(5,1),O(0,0),
∴B(5﹣2,1+4),
即B(3,5),
故答案为:(3,5);
(2)将B(3,5)代入y=kx+b,得:3k+b=5,
∴b=5﹣3k;
(3)一次函数y=kx+b(k、b为常数,且k≠0)的图象过点B,
∴当一次函数y=kx+b的图象将平行四边形OABC分成面积相等的两部分时,图象必过(0,0)点,
由(2)知:y=kx+5﹣3k,
∴5﹣3k=0,
∴;
(4)当直线y=kx+b经过A点时,得,
解得:,
当直线y=kx+b经过C点时,得,
解得:k=﹣2,
∵一次函数y=kx+b的图象与平行四边形OABC的边只有两个公共点,
∴或k<﹣2.
16.【解答】(1)证明:∵CD=AD,
∴∠C=∠DAC,
∴∠ADB=∠C+∠DAC=2∠C;
∵∠B=2∠C,
∴∠ADB=∠B,
∴AD=AB;
(2)解:如图,连接AE,
由(1)知,AD=AB,
又∵E是BD的中点,
∴AE⊥BD,
∴△AEC是直角三角形,
∵F是AC的中点,AC=6,
∴.
17.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠B+∠ECD=180°,
∵∠AFE=∠B,
∴∠AFE+∠ECD=180°,
又∵∠AFE+∠AFD=180°,
∴∠AFD=∠ECD;
(2)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC,
在△AFD和△DCE中,
,
∴△AFD≌△DCE(AAS),
(3)解:过点E作EH⊥AB于H,如图所示:
由(2)可知:△AFD≌△DCE,
∴DF=CE,AF=CD,
∵四边形ABCD为平行四边形,
∴BC=AD,AB=CD,
∵AD=DE,
∴BC=DE,
∵DE=DF+EF=CE+EF,BC=CE+BE,
∴BE=EF,
∵AB=CD,CD=DF,AF=CD,DF=CE,
∴AB=AF=CD=CE,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(SSS),
∴∠AEB=∠AEF,
∴∠B=60°,
∴∠C=180°﹣∠B=120°,
∵CD=CE,
∴∠CED=∠CDE(180°﹣∠C)=30°,
∴∠BEF=180°﹣∠CED=150°,
∴∠AEB=∠AEF∠BEF=75°,
∵EH⊥AB,∠B=60°,
∴∠BEH=30°,
∴∠AEH=∠AEB﹣∠BEH=45°,
∴△AHE为等腰直角三角形,即HE=HA,
在Rt△BEH中,∠∠BEH=30°,BE=2,
∴BHBE=1,
由勾股定理得:HE,
∴HE=HA,
∴AE.
18.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,BD=2DO=2BO,
∴∠ADO=∠CBO,
∵BD=2AD,
∴AD=BO=BC,
∴△BOC是等腰三角形,
∵OE=CE,
∴∠OBE=∠CBE∠ADO,
∴∠ADO=2∠OBE.
(2)①证明:∵△BOC是等腰三角形,E是CO中点,
∴EB⊥CO,
∴∠BEA=90°,
∵G为AB中点,
∴EGAB,
∵E、F分别是OC、OD的中点,
∴EFCD,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴EG=EF,
∴△EFG是等腰三角形.
②解:由题意知,EF∥CD∥BG,
∴EFAB=BG,
∴四边形BEFG是平行四边形,
∴∠EFG=∠GBE,
∵∠FEG=∠AEB=90°,
∴△EFG∽△EBA,
∴△ABE是等腰三角形,
∴∠BAE=∠ABE=45°,
∴EG⊥AB,
设AG=GE=x,则BE=AEx,CE,
在Rt△BCE中,由勾股定理得,BC2=BE2+CE2,即,
解得x=3或x=﹣3(不合题意,舍去),
∴BE=3,AC=4CE=4,
∴S平行四边形ABCD=2120,
∴平行四边形ABCD的面积为120.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
