2.1 一元二次方程 课件(共23张PPT)
文档属性
| 名称 | 2.1 一元二次方程 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 18:22:11 | ||
图片预览








文档简介
(共23张PPT)
2.1 一元二次方程
第一章 二次根式
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
01
02
03
1.理解一元二次方程及其相关概念,能够熟练地把一元二次方程化为一般形式.
2. 应用一元二次方程的解的定义解决有关问题.
3. 在分析、揭示实际问题中的数量关系,并把实际问题转化为数学模型的过程中,感受方程是刻画现实世界中的数量关系的工具,增强对一元二次方程的感性认识.
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
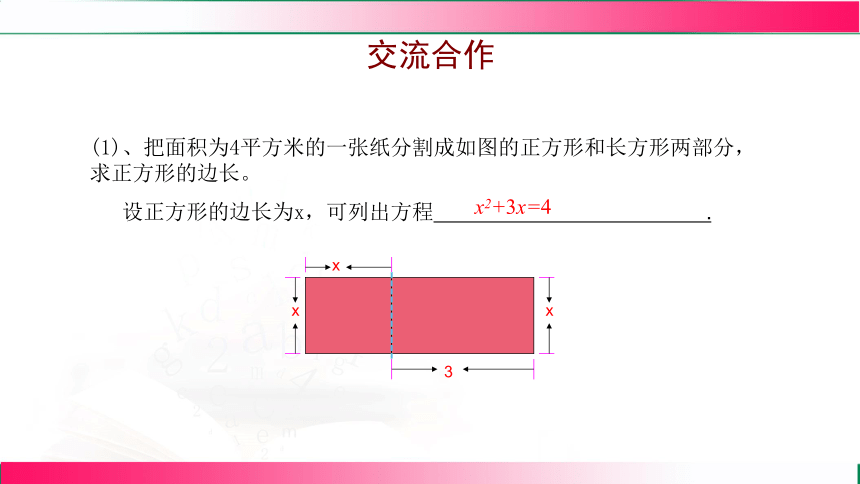
交流合作
(1)、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程 .
x2+3x=4
x
x
x
3
交流合作
(2)某放射性元素经2天后,质量衰变为原来的 ,这种放射性元素平均每天减少率为多少? 设年平均每天减少率为x,可列出方程 。
(1-x)2 =
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
设五个连续整数中第一个为x ,那么后四个数为 、 、
、 ,根据题意,
得方程: .
(3)观察下面等式:
知识讲解
x2-8x-20=0
观察下列三个方程:
x2+3x=4
x2-8x-20=0
(1-x)2 =
它们有什么共同特点?
1、只含有一个未知数;
2、都是整式方程;
4、都可以化成 的形式;
a 为二次项系数、b为一次项系数、c为常数,a≠0
3、未知数的最高次数为2;
知识讲解
只含有一个未知数x的整式方程,并且都可以化成ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
一元二次方程的定义:
一元二次方程
①方程两边都是整式
②只含有一个未知数
③未知数的最高次数是2次
想一想
为什么要限制a≠0,b,c可以为零吗?
一般地,任何一个关于x 的一元二次方程都可以化为 c为常数,a≠0) 的形式,我们把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2,bx,c分别称为二次项、一次项和常数项.
ax2+bx+c=0(a ,b ,
1、二次项系数为负数时,一般要化为正数;
2、写一般式时通常按未知数的次数从高到低排列;
3、写系数时要带上前面的符号.
友情提示
知识讲解
行业PPT模板http:///hangye/
例1、把方程 化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
原方程去括号:
移项:
合并同类项得:
二次项系数:5 一次项系数:36 常数项:-32
化一般式的方法:
一去(去分母、去括号)
二移(移项)
三并(合并同类项)
典例精讲
例2 下列方程中哪些是一元二次方程?
(7)x(x-2)=x2+19
典例精讲
√
√
√
×有两个未知数
×要a≠0
×方程要整式
×化简后x2抵消了
知识讲解
能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).
下列哪些数是方程 x2–x–6= 0 的根
-2, -1, 0, 1, 2, 3
∴-2和3是方程 x2–x–6= 0 的根
所以,-2 是方程 x2–x–6= 0 的根
所以,-1 不是方程 x2–x–6= 0 的根
类似地,把0, 1, 2, 3代入方程 x2–x–6= 0 验算
例3 已知一元二次方程 2x2+bx+c=0 的两个根为 和 ,求这个方程。
典例精讲
2·(-3)2 +(-3)b+c=0
2·()2 +b+c=0
解:由题意得,把 x= -3和 x= 代入方程2x2+bx+c=0 得,
b= 1
c= -15
∴这个方程是 2x2 + x -15 =0
典例精讲
例4 已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值。
解:由题意得,把x=3代入方程x2+ax+a=0得,
32+3a+a= 0
9+4a= 0
4a= -9
方程 一般式 二次项系数 一次项系数 常数项
x2-4x-3=0
0.5x2=√5
√2y-4y2=0
(2x)2=(x+1)2
举一反三
x2-4x-3=0
1
-4
-3
0.5
0
0.5x2-√5 =0
-4y2 +√2y =0
-4
0
√2
3x2-2x-1=0
3
-2
-1
- √5
知识点1 利用提公因式法分解因式解方程
1. [2024·杭州拱墅区期末] 方程 的两个根的和是
( )
C
A. B. 0 C. 2 D. 4
【点拨】 ,
或 .
, .
.故选C.
返回
2. 一元二次方程 的根是
________________.
,
【点拨】 ,
.
则或 ,
解得, .
返回
3.已知某三角形两边长为3和5,第三边长满足方程
,则这个三角形的形状是__________
__.
返回
直角三角形
4.解下列方程:
(1) ;
【解】 ,
.
则或 ,
解得, .
(2) ;
,
.
.
则或 ,
解得, .
(3) ;
,
.
,即 .
则或 ,
解得, .
(4) .
,
化简方程,得 .
.
则或 ,
解得, .
返回
课堂小结
谢谢观看!
2.1 一元二次方程
第一章 二次根式
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
01
02
03
1.理解一元二次方程及其相关概念,能够熟练地把一元二次方程化为一般形式.
2. 应用一元二次方程的解的定义解决有关问题.
3. 在分析、揭示实际问题中的数量关系,并把实际问题转化为数学模型的过程中,感受方程是刻画现实世界中的数量关系的工具,增强对一元二次方程的感性认识.
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
交流合作
(1)、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程 .
x2+3x=4
x
x
x
3
交流合作
(2)某放射性元素经2天后,质量衰变为原来的 ,这种放射性元素平均每天减少率为多少? 设年平均每天减少率为x,可列出方程 。
(1-x)2 =
你还能找到其他的五个连续整数,使前三个数的平方和等于后两个数的平方和吗?
设五个连续整数中第一个为x ,那么后四个数为 、 、
、 ,根据题意,
得方程: .
(3)观察下面等式:
知识讲解
x2-8x-20=0
观察下列三个方程:
x2+3x=4
x2-8x-20=0
(1-x)2 =
它们有什么共同特点?
1、只含有一个未知数;
2、都是整式方程;
4、都可以化成 的形式;
a 为二次项系数、b为一次项系数、c为常数,a≠0
3、未知数的最高次数为2;
知识讲解
只含有一个未知数x的整式方程,并且都可以化成ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
一元二次方程的定义:
一元二次方程
①方程两边都是整式
②只含有一个未知数
③未知数的最高次数是2次
想一想
为什么要限制a≠0,b,c可以为零吗?
一般地,任何一个关于x 的一元二次方程都可以化为 c为常数,a≠0) 的形式,我们把ax2+bx+c=0(a,b,c为常数,a≠0)称为一元二次方程的一般形式,其中ax2,bx,c分别称为二次项、一次项和常数项.
ax2+bx+c=0(a ,b ,
1、二次项系数为负数时,一般要化为正数;
2、写一般式时通常按未知数的次数从高到低排列;
3、写系数时要带上前面的符号.
友情提示
知识讲解
行业PPT模板http:///hangye/
例1、把方程 化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
原方程去括号:
移项:
合并同类项得:
二次项系数:5 一次项系数:36 常数项:-32
化一般式的方法:
一去(去分母、去括号)
二移(移项)
三并(合并同类项)
典例精讲
例2 下列方程中哪些是一元二次方程?
(7)x(x-2)=x2+19
典例精讲
√
√
√
×有两个未知数
×要a≠0
×方程要整式
×化简后x2抵消了
知识讲解
能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).
下列哪些数是方程 x2–x–6= 0 的根
-2, -1, 0, 1, 2, 3
∴-2和3是方程 x2–x–6= 0 的根
所以,-2 是方程 x2–x–6= 0 的根
所以,-1 不是方程 x2–x–6= 0 的根
类似地,把0, 1, 2, 3代入方程 x2–x–6= 0 验算
例3 已知一元二次方程 2x2+bx+c=0 的两个根为 和 ,求这个方程。
典例精讲
2·(-3)2 +(-3)b+c=0
2·()2 +b+c=0
解:由题意得,把 x= -3和 x= 代入方程2x2+bx+c=0 得,
b= 1
c= -15
∴这个方程是 2x2 + x -15 =0
典例精讲
例4 已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值。
解:由题意得,把x=3代入方程x2+ax+a=0得,
32+3a+a= 0
9+4a= 0
4a= -9
方程 一般式 二次项系数 一次项系数 常数项
x2-4x-3=0
0.5x2=√5
√2y-4y2=0
(2x)2=(x+1)2
举一反三
x2-4x-3=0
1
-4
-3
0.5
0
0.5x2-√5 =0
-4y2 +√2y =0
-4
0
√2
3x2-2x-1=0
3
-2
-1
- √5
知识点1 利用提公因式法分解因式解方程
1. [2024·杭州拱墅区期末] 方程 的两个根的和是
( )
C
A. B. 0 C. 2 D. 4
【点拨】 ,
或 .
, .
.故选C.
返回
2. 一元二次方程 的根是
________________.
,
【点拨】 ,
.
则或 ,
解得, .
返回
3.已知某三角形两边长为3和5,第三边长满足方程
,则这个三角形的形状是__________
__.
返回
直角三角形
4.解下列方程:
(1) ;
【解】 ,
.
则或 ,
解得, .
(2) ;
,
.
.
则或 ,
解得, .
(3) ;
,
.
,即 .
则或 ,
解得, .
(4) .
,
化简方程,得 .
.
则或 ,
解得, .
返回
课堂小结
谢谢观看!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
