3.3方差与标准差 课件(共26张PPT)
文档属性
| 名称 | 3.3方差与标准差 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 18:38:09 | ||
图片预览








文档简介
(共26张PPT)
3.3方差与标准差
第3章 数据分析初步
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
0
1
2
2
3
4
5
4
6
8
10
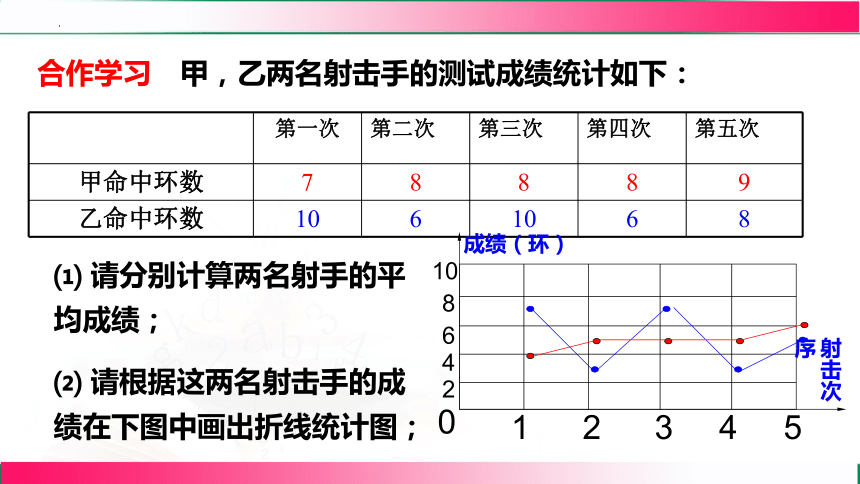
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在下图中画出折线统计图;
合作学习
1.一般地,各数据与平均数的____的______________
_____________________________________叫做这组数据的
方差.
差
平方的平均数
2.一般地,一组数据的______的____________
_ ______________________________________称为这组数据
的标准差.
方差
算术平方根
3.方差是用来衡量一组数据的__________的统计量,方差
______,数据的波动就______;方差______,数据的波动就
______.
波动大小
越小
越小
越大
越大
4.方差反映的是一组数据与平均数的__________,即数据的
__________.
偏离程度
波动程度
知识点1 方差
1. [2024·杭州上城区期中] 已知数据,, , 的方差计算
公式为 ,则
“4”是这组数据的( )
C
A. 方差 B. 中位数 C. 平均数 D. 众数
返回
2. 甲、乙、丙、丁四名射击运动员进行射击测试,每人10次
射击成绩的平均数(单位:环)及方差(单位:环 )如
表所示,根据表中数据,要从中选择一名成绩好且发挥稳定
的运动员参加比赛,应选择( )
甲 乙 丙 丁
9 8 9 8
1.6 0.8 0.8 3
C
A. 甲 B. 乙 C. 丙 D. 丁
返回
3. 为迎接2025年体育中考,甲、乙、丙三
名男生参加1 000米长跑训练,体育老师根据训练成绩得出
他们的成绩的方差分别为,, ,
则____的成绩较稳定(填“甲”“乙”或“丙”).
乙
4.已知一组数据为7,1,5, ,8,它们的平均数是5,则这
组数据的方差为___.
6
返回
知识点2 标准差
5. 已知一组数据的方差是3,则这组数据的标准差是( )
D
A. 9 B. 3 C. D.
6. 下列五个数:11,12,13,14,15的标准
差为____.
返回
7. 已知一组数据为7,2,5, ,8,它
们的平均数是5,则这组数据的标准差是_ ____.
【点拨】 这组数据7,2,5, ,8的平均数为5,
,解得 ,
.
这组数据的标准差是 .
返回
8. 某校模拟考试中,九年级(1)班的六名学生的数学成绩
(单位:分)如下:96,108,102,110,108,82.下列说法
不正确的是( )
D
A. 众数是108分 B. 中位数是105分
C. 方差约是94.3分 D. 标准差是 分
【点拨】把这六名学生的数学成绩从小到大排列为:
82,96,102,108,108,110,
众数是108分,中位数为 (分),平均数为
(分) 方差为
(分) 标准差不是 分.故选D.
返回
思考
根据统计图,思考下列问题.
(1)甲乙两名射击手他们每次的射击成绩与他们的平均成绩比较,哪一个偏离程度较低
(2)射击成绩偏离平均数的程度和数据的离散程度与折线的波动情况有怎样的联系
(3)用怎样的特征数来表示数据的偏离程度 可否用各个数据与平均数的差的累计数来表示数据的偏离程度
(4)是否可用各个数据与平均数的差的平方和来表示数据的偏离程度
(5)数据的偏离程度还与什么有关 要比较两组样本容量不相同的数据偏离平均数的程度,应如何比较
要挑选一名射击手参加比赛,你认为挑选哪一位比较适合 为什么
(7-8)2+
(8-8)2+
(9-8)2
(8-8)2+
(8-8)2+
甲:
=2
(10-8)2+
(6-8)2+
(8-8)2
(6-8)2+
(10-8)2+
乙:
=16
请计算甲乙两名运动员每次射击成绩与平均成绩的偏差的平方和
为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐
解
1
10
X甲=
(12+13+14+15+10+16+13+11+15+11)=13(cm);
1
10
X乙=
(11+16+17+14+13+19+6+8+10+16)=13(cm);
例
s甲2=
1
10
(10-13)2+
(14-13)2+
(15-13)2+
(16-13)2+
(13-13)2+
[(12-13)2+
(13-13)2+
(11-13)2+
(15-13)2+
(11-13)2]
=3.6(cm2);
s甲2=
1
10
(10-13)2+
(14-13)2+
(15-13)2+
(16-13)2+
(13-13)2+
[(12-13)2+
(13-13)2+
(11-13)2+
(15-13)2+
(11-13)2]
S乙2=
1
10
(13-13)2+
(17-13)2+
(14-13)2+
(19-13)2+
(6-13)2+
[(11-13)2+
(16-13)2+
(8-13)2+
(10-13)2+
(16-13)2]
=15.8(cm2).
因为
S2甲<S2乙,
所以甲种小麦长得比较整齐.
甲 99 103 98 101 104 100 98 97
乙 102 100 95 103 105 96 98 101
S甲2= 5.5(克2) S乙2=10.5(克2)
甲 9.9 10.3 9.8 10.1 10.4 10 9.8 9.7
乙 10.2 10 9.5 10.3 10.5 9.6 9.8 10.1
S甲2= 0.055(克2) S乙2=0.105(克2)
(单位:克)
根据下表求出方差
(1) 方差越大,说明数据的波动 , 越 。
(2) 方差的单位和数据的单位是一致吗
为使单位一致,怎么办
用方差的算术平方根:
S=
[(x1-x)2+ (x2-x)2+ · · ·+(xn-x)2]
√
并把它叫做标准差(standard deviation)
越大
不稳定
议一议:
合作探究
已知三组数据1、2、3、4、5;11、12、13、14、15和3、6、9、12、15。
1、求这三组数据的平均数、方差和标准差。
2、对照以上结果,你能从中发现哪些有趣的结论?
平均数 方差 标准差
1、2、3、4、5
11、12、13、14、15
3、6、9、12、15
3
2
2
13
2
2
2
3
9
18
已知数据 和数据
且
若数据 的方差为
若数据 的方差为
则
合作探究
1、已知数据x1,x2,x3,… xn的平均数为 ,方差为 ,标准差为S。则
①数据x1+3,x2 + 3,x3 +3 ,… xn+3的平均数为_______
方差为_______ , 标准差为_______ 。
②数据x1-3,x2 -3,x3-3 ,… xn-3的平均数为_______ 方差为_______ , 标准差为_______ 。
做一做:
3、已知数据x1、x2、x3、x4、x5的方差是 3, 那么数据x1-1,x2-1,x3-1,x4-1,x5-1的方差是( )
(A)1 (B)2 (C)3 (D)4
C
做一做:
一组数据中,各数据与它们的平均数的差的平方的平均数。
方差:
计算公式:
一般步骤:
求平均-再求差-然后平方-最后再平均
谢谢观看!
3.3方差与标准差
第3章 数据分析初步
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在下图中画出折线统计图;
合作学习
1.一般地,各数据与平均数的____的______________
_____________________________________叫做这组数据的
方差.
差
平方的平均数
2.一般地,一组数据的______的____________
_ ______________________________________称为这组数据
的标准差.
方差
算术平方根
3.方差是用来衡量一组数据的__________的统计量,方差
______,数据的波动就______;方差______,数据的波动就
______.
波动大小
越小
越小
越大
越大
4.方差反映的是一组数据与平均数的__________,即数据的
__________.
偏离程度
波动程度
知识点1 方差
1. [2024·杭州上城区期中] 已知数据,, , 的方差计算
公式为 ,则
“4”是这组数据的( )
C
A. 方差 B. 中位数 C. 平均数 D. 众数
返回
2. 甲、乙、丙、丁四名射击运动员进行射击测试,每人10次
射击成绩的平均数(单位:环)及方差(单位:环 )如
表所示,根据表中数据,要从中选择一名成绩好且发挥稳定
的运动员参加比赛,应选择( )
甲 乙 丙 丁
9 8 9 8
1.6 0.8 0.8 3
C
A. 甲 B. 乙 C. 丙 D. 丁
返回
3. 为迎接2025年体育中考,甲、乙、丙三
名男生参加1 000米长跑训练,体育老师根据训练成绩得出
他们的成绩的方差分别为,, ,
则____的成绩较稳定(填“甲”“乙”或“丙”).
乙
4.已知一组数据为7,1,5, ,8,它们的平均数是5,则这
组数据的方差为___.
6
返回
知识点2 标准差
5. 已知一组数据的方差是3,则这组数据的标准差是( )
D
A. 9 B. 3 C. D.
6. 下列五个数:11,12,13,14,15的标准
差为____.
返回
7. 已知一组数据为7,2,5, ,8,它
们的平均数是5,则这组数据的标准差是_ ____.
【点拨】 这组数据7,2,5, ,8的平均数为5,
,解得 ,
.
这组数据的标准差是 .
返回
8. 某校模拟考试中,九年级(1)班的六名学生的数学成绩
(单位:分)如下:96,108,102,110,108,82.下列说法
不正确的是( )
D
A. 众数是108分 B. 中位数是105分
C. 方差约是94.3分 D. 标准差是 分
【点拨】把这六名学生的数学成绩从小到大排列为:
82,96,102,108,108,110,
众数是108分,中位数为 (分),平均数为
(分) 方差为
(分) 标准差不是 分.故选D.
返回
思考
根据统计图,思考下列问题.
(1)甲乙两名射击手他们每次的射击成绩与他们的平均成绩比较,哪一个偏离程度较低
(2)射击成绩偏离平均数的程度和数据的离散程度与折线的波动情况有怎样的联系
(3)用怎样的特征数来表示数据的偏离程度 可否用各个数据与平均数的差的累计数来表示数据的偏离程度
(4)是否可用各个数据与平均数的差的平方和来表示数据的偏离程度
(5)数据的偏离程度还与什么有关 要比较两组样本容量不相同的数据偏离平均数的程度,应如何比较
要挑选一名射击手参加比赛,你认为挑选哪一位比较适合 为什么
(7-8)2+
(8-8)2+
(9-8)2
(8-8)2+
(8-8)2+
甲:
=2
(10-8)2+
(6-8)2+
(8-8)2
(6-8)2+
(10-8)2+
乙:
=16
请计算甲乙两名运动员每次射击成绩与平均成绩的偏差的平方和
为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐
解
1
10
X甲=
(12+13+14+15+10+16+13+11+15+11)=13(cm);
1
10
X乙=
(11+16+17+14+13+19+6+8+10+16)=13(cm);
例
s甲2=
1
10
(10-13)2+
(14-13)2+
(15-13)2+
(16-13)2+
(13-13)2+
[(12-13)2+
(13-13)2+
(11-13)2+
(15-13)2+
(11-13)2]
=3.6(cm2);
s甲2=
1
10
(10-13)2+
(14-13)2+
(15-13)2+
(16-13)2+
(13-13)2+
[(12-13)2+
(13-13)2+
(11-13)2+
(15-13)2+
(11-13)2]
S乙2=
1
10
(13-13)2+
(17-13)2+
(14-13)2+
(19-13)2+
(6-13)2+
[(11-13)2+
(16-13)2+
(8-13)2+
(10-13)2+
(16-13)2]
=15.8(cm2).
因为
S2甲<S2乙,
所以甲种小麦长得比较整齐.
甲 99 103 98 101 104 100 98 97
乙 102 100 95 103 105 96 98 101
S甲2= 5.5(克2) S乙2=10.5(克2)
甲 9.9 10.3 9.8 10.1 10.4 10 9.8 9.7
乙 10.2 10 9.5 10.3 10.5 9.6 9.8 10.1
S甲2= 0.055(克2) S乙2=0.105(克2)
(单位:克)
根据下表求出方差
(1) 方差越大,说明数据的波动 , 越 。
(2) 方差的单位和数据的单位是一致吗
为使单位一致,怎么办
用方差的算术平方根:
S=
[(x1-x)2+ (x2-x)2+ · · ·+(xn-x)2]
√
并把它叫做标准差(standard deviation)
越大
不稳定
议一议:
合作探究
已知三组数据1、2、3、4、5;11、12、13、14、15和3、6、9、12、15。
1、求这三组数据的平均数、方差和标准差。
2、对照以上结果,你能从中发现哪些有趣的结论?
平均数 方差 标准差
1、2、3、4、5
11、12、13、14、15
3、6、9、12、15
3
2
2
13
2
2
2
3
9
18
已知数据 和数据
且
若数据 的方差为
若数据 的方差为
则
合作探究
1、已知数据x1,x2,x3,… xn的平均数为 ,方差为 ,标准差为S。则
①数据x1+3,x2 + 3,x3 +3 ,… xn+3的平均数为_______
方差为_______ , 标准差为_______ 。
②数据x1-3,x2 -3,x3-3 ,… xn-3的平均数为_______ 方差为_______ , 标准差为_______ 。
做一做:
3、已知数据x1、x2、x3、x4、x5的方差是 3, 那么数据x1-1,x2-1,x3-1,x4-1,x5-1的方差是( )
(A)1 (B)2 (C)3 (D)4
C
做一做:
一组数据中,各数据与它们的平均数的差的平方的平均数。
方差:
计算公式:
一般步骤:
求平均-再求差-然后平方-最后再平均
谢谢观看!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
