4.5 三角形的中位线 课件(共31张PPT)
文档属性
| 名称 | 4.5 三角形的中位线 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:55:39 | ||
图片预览




文档简介
(共31张PPT)
4.5 三角形的中位线
第4章 平行四边形
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
C
B
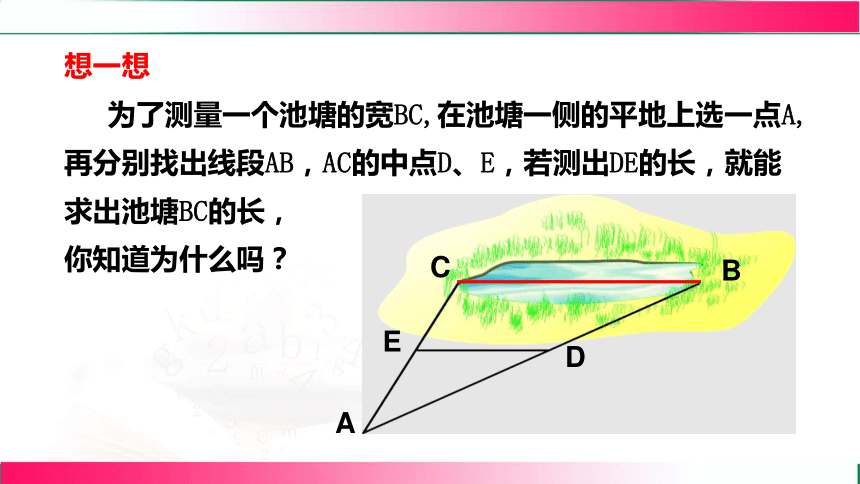
B、C两点被池塘隔开如何测量B、C两点距离?
想一想
A
B
C
D
E
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,就能求出池塘BC的长,
你知道为什么吗?
想一想
A
B
C
D
E
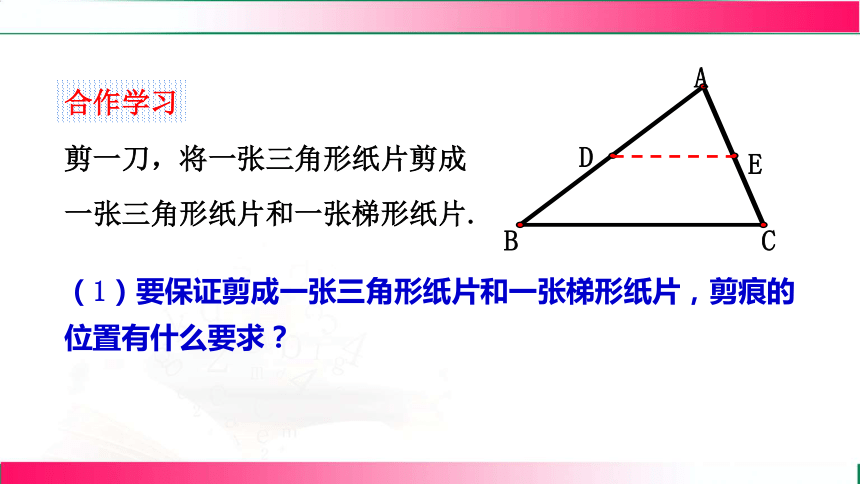
合作学习
剪一刀,将一张三角形纸片剪成
一张三角形纸片和一张梯形纸片.
(1)要保证剪成一张三角形纸片和一张梯形纸片,剪痕的位置有什么要求?
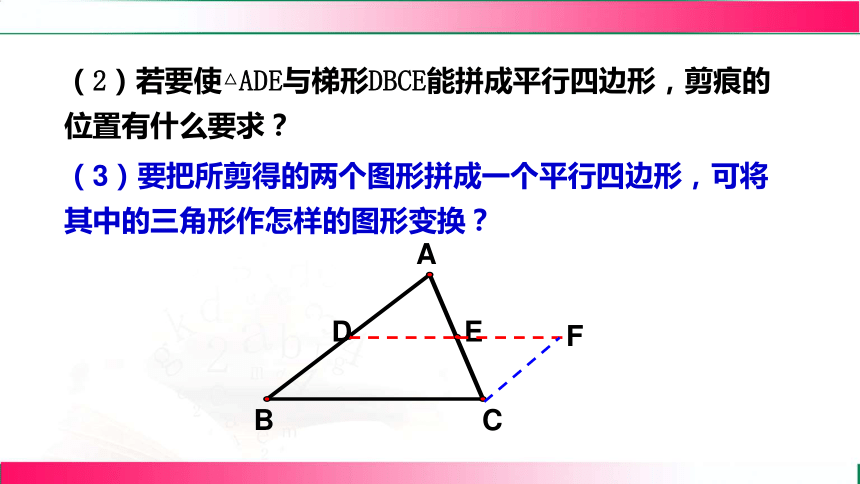
(2)若要使△ADE与梯形DBCE能拼成平行四边形,剪痕的位置有什么要求?
(3)要把所剪得的两个图形拼成一个平行四边形,可将其中的三角形作怎样的图形变换?
A
B
C
D
E
F
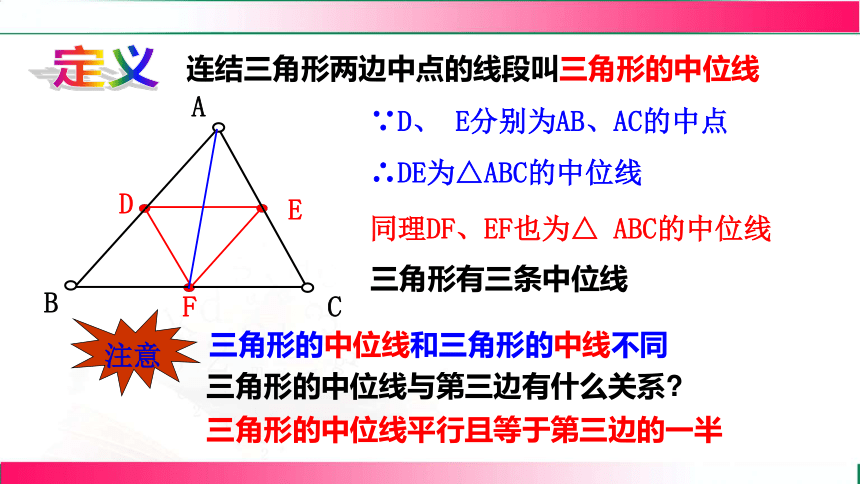
连结三角形两边中点的线段叫三角形的中位线
三角形有三条中位线
∵D、 E分别为AB、AC的中点
∴DE为△ABC的中位线
三角形的中位线和三角形的中线不同
注意
同理DF、EF也为△ ABC的中位线
E
D
F
A
C
B
定义
三角形的中位线与第三边有什么关系
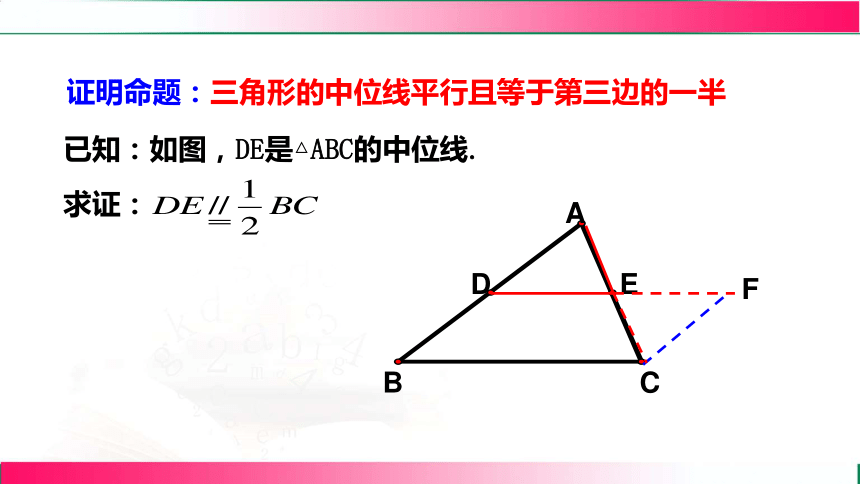
三角形的中位线平行且等于第三边的一半
已知:如图,DE是△ABC的中位线.
求证:
A
B
C
D
E
F
证明命题:三角形的中位线平行且等于第三边的一半
证明:如图,以点E为旋转中心,把⊿ADE绕点E,按顺时针方向旋转180゜,得到⊿CFE,
A
B
C
D
E
F
⊿ADE≌⊿CFE.
∴∠ADE=∠F,AD=CF,DE=EF
∴AB∥CF
又∵BD=AD=CF,
∴四边形BCFD是平行四边形
证明二:如图,延长DE到F,使EF=DE,连接CF
∴∠ADE=∠F,AD=CF,
∴AB∥CF
又∵BD=AD=CF,
∴四边形BCFD是平行四边形
A
B
C
D
E
F
∵DE=EF,AE=EC, ∠AED= ∠CEF
∴⊿ADE≌⊿CFE
A
B
C
E
D
F
证法三:延长DE到点F,使EF=DE, 连结AF、CF、CD
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形 ∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形
证法四:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G ∵AG∥BC ∴∠EAG=∠ECF
∴△AEG≌△CEF ∴AG=FC,GE=EF
又∵AB∥GF,AG∥BF
∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF又∵D为AB中点,E为GF中点,
∴DB∥=EF∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC即DE=1/2BC
A
B
C
E
D
F
G
三角形中位线定理
三角形的中位线平行且等于第三边的一半.
几何语言表述:
∵DE是△ABC的中位线(或AD=BD,AE=CE)
C
E
D
B
A
① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半
适用范围
例1、已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
A
B
C
D
E
F
G
H
顺次连接四边形各边中点的线段组成一个平行四边形
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线
温馨提示:
(1) 顺次连结平行四边形各边中点所得的四边形是_________?
(2)顺次连结矩形各边中点所得的四边形是_______?
(3)顺次连结菱形各边中点所得的四边形是________?
平行四边形
菱形
矩形
想一想
(4)顺次连结正方形各边中点所得的四边形是___________?
(5)顺次连结梯形各边中点所得的四边形是______________?
(6)顺次连结等腰梯形各边中点所得的四边形是__________?
正方形
平行四边形
菱形
想一想
(7)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
想一想
(9)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
想一想
正方形
知识点 三角形的中位线
(第1题)
1. 如图,某小区居民为了美
化居住环境,要在一块三角形空地 上围一
个四边形花坛.已知点,分别是边 ,
的中点,量得米,则边 的长是
( )
C
A. 6米 B. 7米 C. 8米 D. 9米
返回
(第2题)
2. 如图,在中,, ,
,是中位线,则 的长为( )
A
A. 2 B. 3 C. 4 D.
返回
3. 如图,在平行四边形中,对角线,交于点 ,
是的中点,连结.若,则 的长为( )
B
(第3题)
A. B. C. D.
返回
(第4题)
4. 如图,在中, , ,
分别是直角边,的中点,连结 ,
则 的度数是( )
B
A. B. C. D.
返回
5. 如图,在中,已知 ,
,,点,,分别是,, 的中
点,则四边形 的周长是____.
13
(第5题)
返回
6. 如图,在中,点,分别为, 的
中点,点在线段上,连结,点,分别为,
的中点.
(1)求证:四边形 为平行四边形;
【证明】 点,分别为, 的中点,
点,分别为, 的中点,
是的中位线,是 的中
位线.
, .
四边形 为平行四边形.
(2)若,, ,求
线段 的长度.
【解】 四边形 为平行四边形,
.
, .
.
返回
(第7题)
7. [2024·杭州拱墅区期中] 如图,在
中,是的中线,,分别是 ,
的中点,连结.已知,则 的长
为( )
A
A. 2 B. 4 C. 6 D. 8
返回
(第8题)
8. 如图,垂直平分的边 ,交
的延长线于点,交于点,是
的中点,连结,.若 ,
,则 的长为( )
C
A. 3 B. 2.5 C. 2 D. 1.5
返回
不相等且不互相垂直的四边形各边中点
组成___________
对角线
平行四边形
互相垂直的四边形各边中点组成______
矩形
相等的四边形各边中点组成_____
菱形
相等且互相垂直的四边形各边中点组成_______
正方形
共同归纳
谢谢观看!
4.5 三角形的中位线
第4章 平行四边形
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
C
B
B、C两点被池塘隔开如何测量B、C两点距离?
想一想
A
B
C
D
E
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,就能求出池塘BC的长,
你知道为什么吗?
想一想
A
B
C
D
E
合作学习
剪一刀,将一张三角形纸片剪成
一张三角形纸片和一张梯形纸片.
(1)要保证剪成一张三角形纸片和一张梯形纸片,剪痕的位置有什么要求?
(2)若要使△ADE与梯形DBCE能拼成平行四边形,剪痕的位置有什么要求?
(3)要把所剪得的两个图形拼成一个平行四边形,可将其中的三角形作怎样的图形变换?
A
B
C
D
E
F
连结三角形两边中点的线段叫三角形的中位线
三角形有三条中位线
∵D、 E分别为AB、AC的中点
∴DE为△ABC的中位线
三角形的中位线和三角形的中线不同
注意
同理DF、EF也为△ ABC的中位线
E
D
F
A
C
B
定义
三角形的中位线与第三边有什么关系
三角形的中位线平行且等于第三边的一半
已知:如图,DE是△ABC的中位线.
求证:
A
B
C
D
E
F
证明命题:三角形的中位线平行且等于第三边的一半
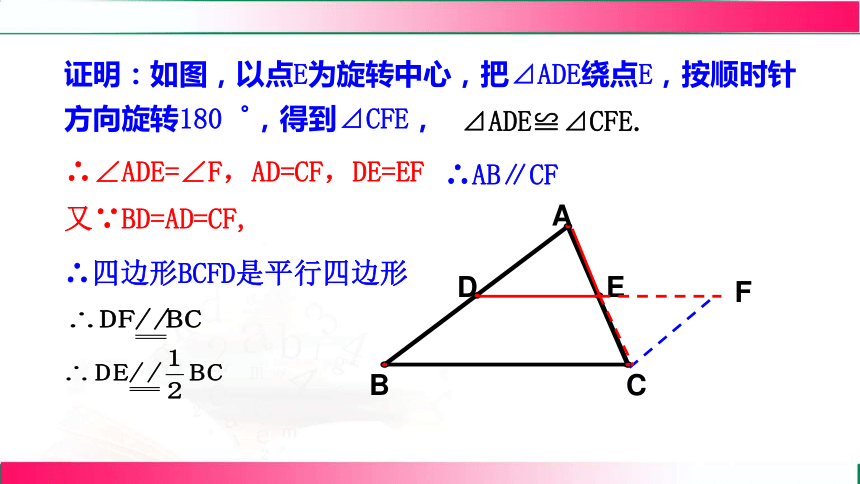
证明:如图,以点E为旋转中心,把⊿ADE绕点E,按顺时针方向旋转180゜,得到⊿CFE,
A
B
C
D
E
F
⊿ADE≌⊿CFE.
∴∠ADE=∠F,AD=CF,DE=EF
∴AB∥CF
又∵BD=AD=CF,
∴四边形BCFD是平行四边形
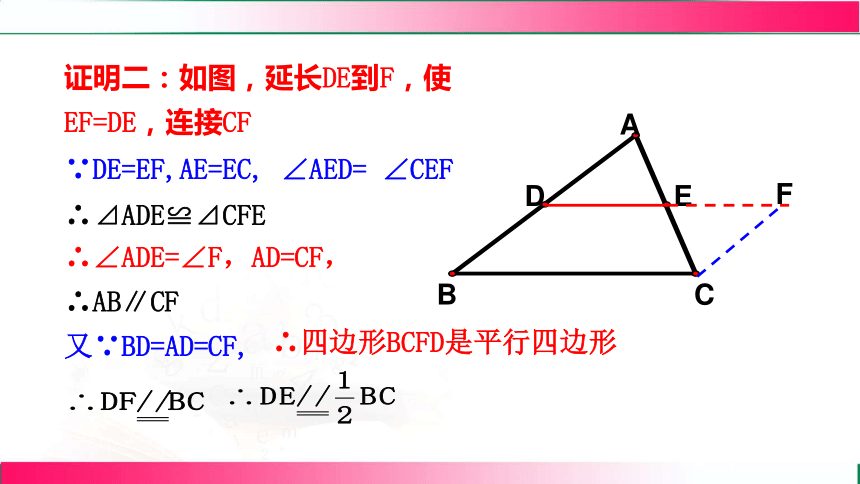
证明二:如图,延长DE到F,使EF=DE,连接CF
∴∠ADE=∠F,AD=CF,
∴AB∥CF
又∵BD=AD=CF,
∴四边形BCFD是平行四边形
A
B
C
D
E
F
∵DE=EF,AE=EC, ∠AED= ∠CEF
∴⊿ADE≌⊿CFE
A
B
C
E
D
F
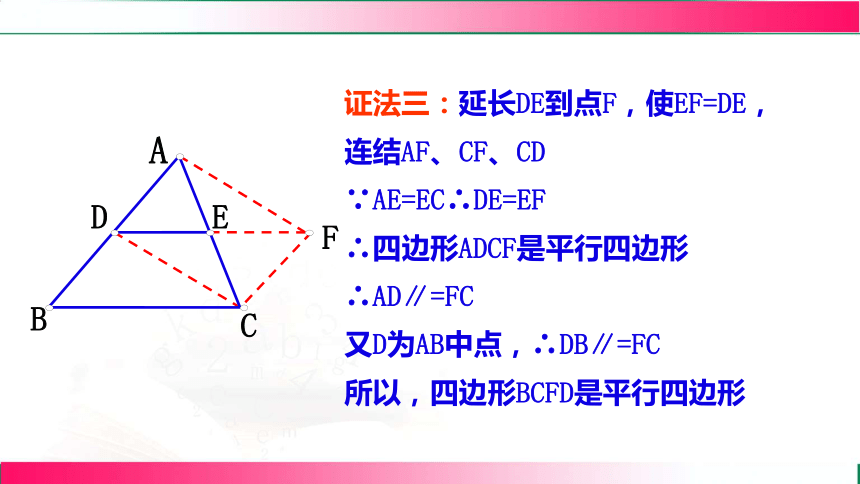
证法三:延长DE到点F,使EF=DE, 连结AF、CF、CD
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形 ∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形
证法四:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G ∵AG∥BC ∴∠EAG=∠ECF
∴△AEG≌△CEF ∴AG=FC,GE=EF
又∵AB∥GF,AG∥BF
∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF又∵D为AB中点,E为GF中点,
∴DB∥=EF∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC即DE=1/2BC
A
B
C
E
D
F
G
三角形中位线定理
三角形的中位线平行且等于第三边的一半.
几何语言表述:
∵DE是△ABC的中位线(或AD=BD,AE=CE)
C
E
D
B
A
① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半
适用范围
例1、已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
A
B
C
D
E
F
G
H
顺次连接四边形各边中点的线段组成一个平行四边形
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线
温馨提示:
(1) 顺次连结平行四边形各边中点所得的四边形是_________?
(2)顺次连结矩形各边中点所得的四边形是_______?
(3)顺次连结菱形各边中点所得的四边形是________?
平行四边形
菱形
矩形
想一想
(4)顺次连结正方形各边中点所得的四边形是___________?
(5)顺次连结梯形各边中点所得的四边形是______________?
(6)顺次连结等腰梯形各边中点所得的四边形是__________?
正方形
平行四边形
菱形
想一想
(7)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
想一想
(9)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
想一想
正方形
知识点 三角形的中位线
(第1题)
1. 如图,某小区居民为了美
化居住环境,要在一块三角形空地 上围一
个四边形花坛.已知点,分别是边 ,
的中点,量得米,则边 的长是
( )
C
A. 6米 B. 7米 C. 8米 D. 9米
返回
(第2题)
2. 如图,在中,, ,
,是中位线,则 的长为( )
A
A. 2 B. 3 C. 4 D.
返回
3. 如图,在平行四边形中,对角线,交于点 ,
是的中点,连结.若,则 的长为( )
B
(第3题)
A. B. C. D.
返回
(第4题)
4. 如图,在中, , ,
分别是直角边,的中点,连结 ,
则 的度数是( )
B
A. B. C. D.
返回
5. 如图,在中,已知 ,
,,点,,分别是,, 的中
点,则四边形 的周长是____.
13
(第5题)
返回
6. 如图,在中,点,分别为, 的
中点,点在线段上,连结,点,分别为,
的中点.
(1)求证:四边形 为平行四边形;
【证明】 点,分别为, 的中点,
点,分别为, 的中点,
是的中位线,是 的中
位线.
, .
四边形 为平行四边形.
(2)若,, ,求
线段 的长度.
【解】 四边形 为平行四边形,
.
, .
.
返回
(第7题)
7. [2024·杭州拱墅区期中] 如图,在
中,是的中线,,分别是 ,
的中点,连结.已知,则 的长
为( )
A
A. 2 B. 4 C. 6 D. 8
返回
(第8题)
8. 如图,垂直平分的边 ,交
的延长线于点,交于点,是
的中点,连结,.若 ,
,则 的长为( )
C
A. 3 B. 2.5 C. 2 D. 1.5
返回
不相等且不互相垂直的四边形各边中点
组成___________
对角线
平行四边形
互相垂直的四边形各边中点组成______
矩形
相等的四边形各边中点组成_____
菱形
相等且互相垂直的四边形各边中点组成_______
正方形
共同归纳
谢谢观看!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
