6.3 反比例函数的应用 课件(共24张PPT)
文档属性
| 名称 | 6.3 反比例函数的应用 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
6.3 反比例函数的应用
第6章 反比例函数
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
知识点
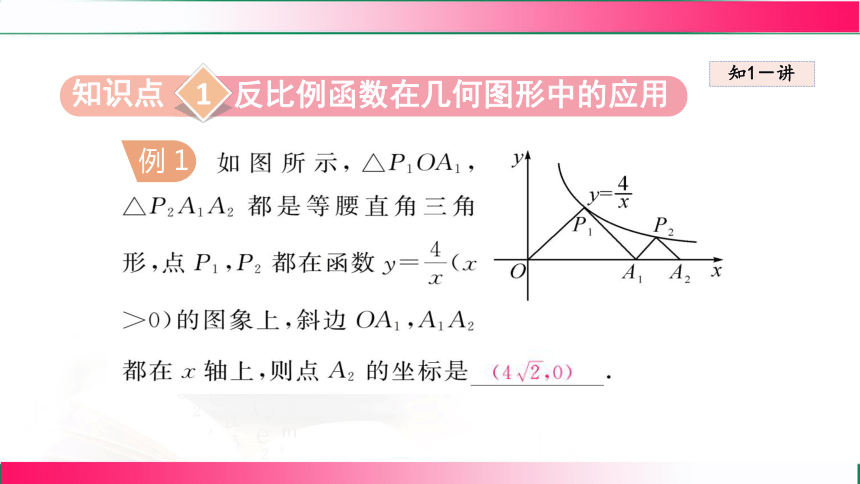
反比例函数在几何图形中的应用
知1-讲
1
例 1
知1-讲
知1-练
知1-练
知2-讲
知识点
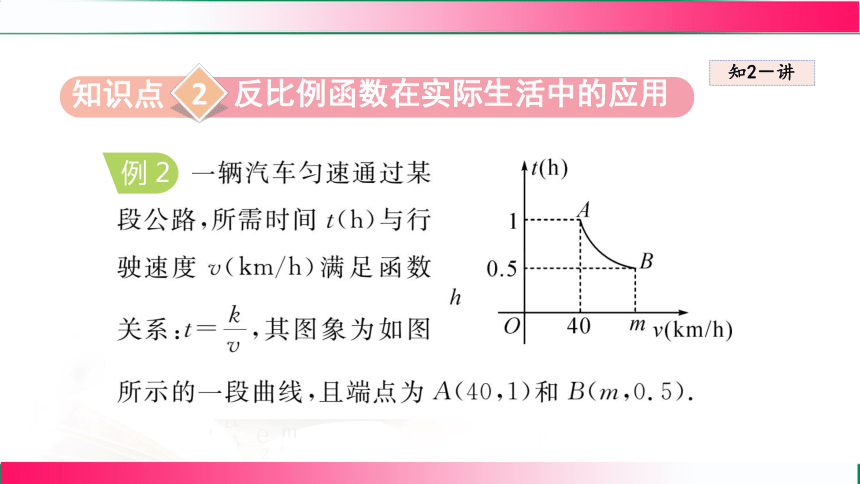
反比例函数在实际生活中的应用
2
例 2
知2-讲
知2-讲
知2-讲
知2-练
知识点1 反比例函数在几何中的应用
1. 面积为2的直角三角形一直角边长为,另一直角边长为 ,
则与 的变化规律用图象大致表示为( )
C
A. B. C. D.
返回
2.菱形的面积为,它的两条对角线的长分别为 ,
,则与之间的函数关系为 ___;这个函数的图象位于
第____象限.
一
返回
知识点2 反比例函数在生活中的应用
3. 科技承载梦想,创新始于少年.某校科技社团的
学生制作了一艘轮船模型,实验过程中他们发现在某段航行过程中
轮船模型的牵引力是其速度 的反比例函数,其图象
如图所示,则下列说法不正确的是 ( )
B
A. 该段航行过程中,随 的增大而减小
B. 当时,
C. 该段航行过程中,反比例函数的表达式为
D. 当时,
返回
4.红红一家人自驾从昆明到丽江游玩,途经一段高速公路,
假设汽车在该高速公路上匀速行驶,记行驶时间为 小时,行
驶速度为 千米/时.若红红爸爸驾车速度为90千米/时,则6小
时可以行完该高速公路.
(1)求与 的函数关系式;
【解】由题意,得 ,
.
(2)他们是早上7:00驶入该高速公路,中午12:00驶离该
高速公路,求红红爸爸在该高速公路上的行驶速度.
(小时),
当时, .
答:红红爸爸在该高速公路上的行驶速度为108千米/时.
返回
知识点3 反比例函数在跨学科中的应用
5. 如果的压力 作用于物体上,产
生的压强要大于,则下列关于物体受力面积 的说
法正确的是( )
A
A. 小于 B. 大于
C. 小于 D. 大于
返回
6. 在一个可以改变体积的密闭容器内装有一
定质量的气体,当改变容器的体积时,气体的
密度也会随之改变,密度 是体积
的反比例函数,它的图象如图所示,当
气体的密度为 时,体积是( )
A
A. B. C. D.
返回
7.如图,根据小孔成像的原理,当像距(小孔到像的距离)
和物高(蜡烛火焰高度)不变时,火焰的像高(单位: )
是物距(小孔到蜡烛的距离)(单位: )的反比例函数,
当时, .
(1)求关于 的函数表达式;
【解】由题意,设 ,
把,代入,得 ,
关于的函数表达式为 .
(2)若火焰的像高为 ,求小孔到蜡烛的距离.
【解】把代入,解得 ,
小孔到蜡烛的距离为 .
返回
课堂小结
反比例函数在其他学科中的应用
在物理学科中,掌握以下关系:
(1)路程一定时,速度与时间成反比例;
(2)电压一定时,电流与电阻成反比例;
(3)气体质量一定时,密度与体积成反比例;
(4)压力一定时,压强与受力面积成反比例;
(5)阻力一定时,动力和动力臂成反比例.
谢谢观看!
6.3 反比例函数的应用
第6章 反比例函数
浙版数学八年级下册
授课教师:********
班 级:********
时 间:********
探究二次根式乘法法则
计算下列各式,观察计算结果,你能发现什么规律?
= ,,所以。
= ,,所以。
= ,,所以。
引导学生观察上述等式,归纳出二次根式的乘法法则:(,)。
用文字语言表述为:两个二次根式相乘,把被开方数相乘,根指数不变。
法则的证明
对于(,),设,,则,。
那么,而。
所以,即(,),证明了二次根式乘法法则的正确性。
(三)例题讲解(15 分钟)
例 1:计算
(1)
解:根据二次根式乘法法则。
(2)
解:。
(3)()
解:。
在讲解例题过程中,强调:
运用法则时要注意被开方数的取值范围,确保,。
计算结果要化为最简二次根式。
(四)课堂练习(10 分钟)
计算
(1)
(2)
(3)()
比较大小:与。
让学生在练习本上完成,教师巡视,及时发现学生存在的问题并进行指导。
(五)课堂小结(5 分钟)
与学生一起回顾二次根式的乘法法则:(,)。
总结运用法则进行计算时的注意事项,如被开方数的取值范围、结果要化为最简二次根式等。
强调从特殊到一般的探究方法以及类比思想在数学学习中的应用。
(六)布置作业(5 分钟)
基础作业
课本课后练习题中关于二次根式乘法运算的题目。
拓展作业
已知,求的取值范围。
若与都有意义,且,请你比较与的大小。
五、教学反思
在本节课的教学过程中,通过复习旧知引入新课,让学生从熟悉的内容过渡到新知识的学习,降低了学习难度。在探究二次根式乘法法则时,让学生通过计算具体式子,观察结果,自己归纳出法则,培养了学生的自主探究能力。在例题讲解和课堂练习环节,大部分学生能够掌握二次根式乘法法则的基本运算,但仍有部分学生在化简结果和处理含有字母的二次根式运算时存在困难,需要在后续的教学中加强辅导和练习。同时,在教学方法上,可以进一步增加一些互动环节,让更多的学生参与到课堂讨论中来,提高课堂的活跃度和学生的学习积极性。
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
知识点
反比例函数在几何图形中的应用
知1-讲
1
例 1
知1-讲
知1-练
知1-练
知2-讲
知识点
反比例函数在实际生活中的应用
2
例 2
知2-讲
知2-讲
知2-讲
知2-练
知识点1 反比例函数在几何中的应用
1. 面积为2的直角三角形一直角边长为,另一直角边长为 ,
则与 的变化规律用图象大致表示为( )
C
A. B. C. D.
返回
2.菱形的面积为,它的两条对角线的长分别为 ,
,则与之间的函数关系为 ___;这个函数的图象位于
第____象限.
一
返回
知识点2 反比例函数在生活中的应用
3. 科技承载梦想,创新始于少年.某校科技社团的
学生制作了一艘轮船模型,实验过程中他们发现在某段航行过程中
轮船模型的牵引力是其速度 的反比例函数,其图象
如图所示,则下列说法不正确的是 ( )
B
A. 该段航行过程中,随 的增大而减小
B. 当时,
C. 该段航行过程中,反比例函数的表达式为
D. 当时,
返回
4.红红一家人自驾从昆明到丽江游玩,途经一段高速公路,
假设汽车在该高速公路上匀速行驶,记行驶时间为 小时,行
驶速度为 千米/时.若红红爸爸驾车速度为90千米/时,则6小
时可以行完该高速公路.
(1)求与 的函数关系式;
【解】由题意,得 ,
.
(2)他们是早上7:00驶入该高速公路,中午12:00驶离该
高速公路,求红红爸爸在该高速公路上的行驶速度.
(小时),
当时, .
答:红红爸爸在该高速公路上的行驶速度为108千米/时.
返回
知识点3 反比例函数在跨学科中的应用
5. 如果的压力 作用于物体上,产
生的压强要大于,则下列关于物体受力面积 的说
法正确的是( )
A
A. 小于 B. 大于
C. 小于 D. 大于
返回
6. 在一个可以改变体积的密闭容器内装有一
定质量的气体,当改变容器的体积时,气体的
密度也会随之改变,密度 是体积
的反比例函数,它的图象如图所示,当
气体的密度为 时,体积是( )
A
A. B. C. D.
返回
7.如图,根据小孔成像的原理,当像距(小孔到像的距离)
和物高(蜡烛火焰高度)不变时,火焰的像高(单位: )
是物距(小孔到蜡烛的距离)(单位: )的反比例函数,
当时, .
(1)求关于 的函数表达式;
【解】由题意,设 ,
把,代入,得 ,
关于的函数表达式为 .
(2)若火焰的像高为 ,求小孔到蜡烛的距离.
【解】把代入,解得 ,
小孔到蜡烛的距离为 .
返回
课堂小结
反比例函数在其他学科中的应用
在物理学科中,掌握以下关系:
(1)路程一定时,速度与时间成反比例;
(2)电压一定时,电流与电阻成反比例;
(3)气体质量一定时,密度与体积成反比例;
(4)压力一定时,压强与受力面积成反比例;
(5)阻力一定时,动力和动力臂成反比例.
谢谢观看!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
