中考数学第一轮复习 圆
图片预览



文档简介
中考数学第一轮复习 圆
【知识梳理】
基本概念: 弧、弦、圆心角、圆周角
确定圆的条件:
基本性质 对称性:
1.圆 垂径定理:
圆心角、弧、弦的关系定理:
圆周角定理:同弧或等弧所对的圆心角是它所对的圆周角的
推论:(1)同弧或等弧所的圆周角
(2)90°的圆周角所对弦是 ,
2. 点与圆的位置关系:( d是指:_________________________________)
_____________;_____________;_____________;
【典型例题】
例1: 如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出弧AC与弧BD的数量关系,并给予证明.
例2:(1)如图1,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点:过点C作CD切⊙O于点D,连结AD交DC于点E.求证:CD=CE
(2)若将图1中的半径OB所在直线向上平行移动交OA于F,交⊙O于B’,其他条件不变(如图2),那么上述结论CD=CE还成立吗 为什么
(3)若将图1中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变(如图3),那么上述结论CD=CE还成立吗 为什么
(图1) (图2) (图3)
例3:在坐标平面内,半径为R的⊙O与x轴交于点D(1,0)、E(5,0),与y轴的正半轴相切于点A。点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线BP,作EH⊥BP于H。
⑴求圆心C的坐标及半径R的值;
⑵△POB和△PHE随点P的运动而变化,若它们全等,
求a的值;
⑶若给定a=6,试判定直线BP与⊙C的位置关系(要
求说明理由)。
【当堂反馈】
1.小红的衣服被一个铁钉划了一个呈直角三角形的一个洞,其中三角形两边长分别为1cm和2cm,若用同色圆形布将此洞全部覆盖,那么这个圆布的直径最小应等于 。
2. 在平面直角坐标系中,以P(2,1)为圆心,r为半径的圆与坐标轴恰好有三个公共点,则r的值为 .
3. 如图,△ABC的三个顶点都在⊙O上,∠ACB=40°,则
∠AOB=____,∠OAB=_____。
4.⊙O的半径为6㎝,OA、OB、OC的长分别为5㎝、6㎝、7㎝,则点A、B、C与⊙O的位置关系是:点A在⊙O_____,点B在⊙O_______。
5. 如图,方格纸上一圆经过(2,5)、(-2,2)、(2,-3,)、(6,2)四点,则该圆圆心的坐标为 ( )
A.(2,-1) B.(2,2) C.(2,1) D.(3,1)
6.已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )
A.40° B.45° C.50° D.65°
7.(2006年金华市)如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.(1)求sin∠BAC的值;(2)如果OE⊥AC,垂足为E,求OE的长;(3)求tan∠ADC的值.(结果保留根号)
【中考聚焦】
1.(长春市)如图1,BD为⊙O的直径,∠A=30°,则∠CBD的度数为( )
A.30° B.60° C.80° D.120°
(1) (2) (3)
2.(绵阳市)如图2,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( ) A.100° B.110° C.120° D.130°
3.(重庆市)如图3,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( ) A.80° B.50° C.40° D.20°
4.(哈尔滨市)半径为6的圆中,圆心角α的余弦值为,则角α所对弦长等于( ) A.4 B.10 C.8 D.6
5. 若一个直角三角形的两边分别为6和8,则这个直角三角形外接圆直径是( )
A.8 B.10 C.5或4 D.10或8
6. 如图4,D为等腰三角形ABC底边BC上的任意一点,AD的延长线交△ABC的外接圆于点E,连接BE、CE,则图中相似 (4)
三角形共有( ) A. 8对 B. 6对 C. 4对 D. 2对
7.下列图形中,各边的中点一定在同一个圆上的是( )
A. 矩形 B. 平行四边形 C. 梯形 D. 对角线互相垂直的四边形
8.已知:⊿ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,
(1)如图1,当∠A为锐角时,连接BE,试判断∠BAC与∠CBE的关系,并证明你的结论;
(2)图1,中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图2,CA的延长线与⊙O相交于E,请问:∠BAC与∠CBE的关系是否与(1)中你所得出的关系相同?若相同加以证明;若不同,请说明理由。
第一轮复习教学案 圆(2)
【知识梳理】
1.直线与圆的位置关系:( d是指:_________________________________)
_____________;_____________;_____________;
2.两圆位置关系:( d是指:_________________________________)____________________;____________________;____________________;____________________;____________________;
3.圆与切线
(1)圆的切线的性质: ;
(2)圆的切线的判定方法:(从定义) ;
(从直线与圆的位置关系) ;
(从判定定理) 。
(3)三角形的内切圆的圆心是 的交点 ,叫做三角形的 。
三角形的外接圆的圆心是 的交点 ,叫做三角形的 。
【典型例题】
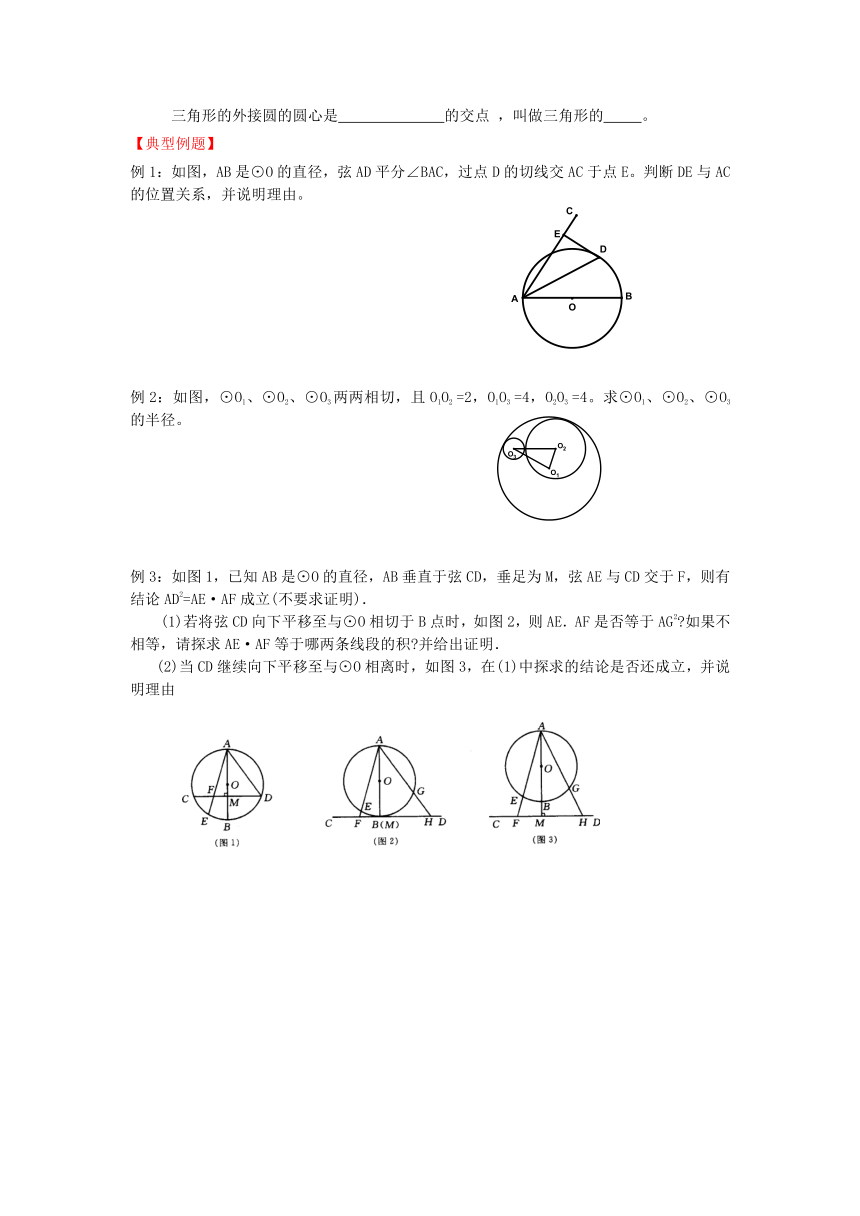
例1:如图,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC于点E。判断DE与AC的位置关系,并说明理由。
例2:如图,⊙O1、⊙O2、⊙O3两两相切,且O1O2 =2,O1O3 =4,O2O3 =4。求⊙O1、⊙O2、⊙O3的半径。
例3:如图1,已知AB是⊙O的直径,AB垂直于弦CD,垂足为M,弦AE与CD交于F,则有结论AD2=AE·AF成立(不要求证明).
(1)若将弦CD向下平移至与⊙O相切于B点时,如图2,则AE.AF是否等于AG2 如果不相等,请探求AE·AF等于哪两条线段的积 并给出证明.
(2)当CD继续向下平移至与⊙O相离时,如图3,在(1)中探求的结论是否还成立,并说明理由
【当堂反馈】
1. 已知两圆的圆心距O1O2为3,⊙O1的半径为1,⊙O2的半径为2,则⊙O1与⊙O2的位置关系为____________________.
2. 若过⊙O内一点M的最长的弦长为6cm,最短的弦长为4cm.则OM的长
为 。
3. 一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是 。
4.已知圆锥的侧面展开图的图心角是72°,它的侧面积为10πcm2,则该圆锥的全面积是 cm2.
5. 已知⊙O的半径为10 cm,如果一条直线和圆心O的距离为10 cm,那么这条直线和这个圆的位置关系为( )
A相离 B.相切 C.相交 D.相交或相切
6. 以O为圆心的两个同心圆的半径分别为11cm和9 cm,若⊙P与这两个圆都相切,则下列说法中正确的是( ).
(A)⊙P的半径可以为2cm
(B)⊙P的半径可以为10 cm
(C)符合条件的点P有无数个且P点运动的路线是曲线
(D)符合条件的⊙P有无数个且P点运动的路线是直线
7. 如图,将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙的切点为A、B,点P是桌子边缘上一点,则∠APB等于( )
A、30° B、45° C、60° D、不能确定
【中考聚焦】
1. 已知关于x的一元二次方程x2-2(R+r)x+d2=0有实数根,其中R、r分别为⊙O1、⊙O2的半径,d为两圆的圆心距,则⊙O1与⊙O2的位置关系是 ( )
A.外离 B.相交 C.相切 D.以上都不正确
2. 如两圆的圆心距等于4,两圆半径分别是R和r,且R、r是方程x2-5x+4=0的两根,则两圆位置关系是( )
A、内含 B、外切 C、相交 D、 外离
3. 设⊙O的半径是r,点O到直线L的距离是d,若⊙O与L至少有一个公共点,则r与d之间的关系是( )
A.d>r B. d=r C. d4.在ΔABC中,∠C=90°,AC=8,AB=10,点P在AC上,AP=2,若⊙O的圆心,O在线段BP上,且⊙O与AB、AC都相切,则⊙O的半径是 ( )
A、1 B、 C、 D、
5.(2007山东临沂)如图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为( )。
A、 B、 C、 D、
6.如图,已知Rt△ABC中,∠B=900,∠A=600,AB=cm.点O从C点出发,沿CB以每秒1cm的速度向B点方向运动,运动到B点时运动停止.当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与BC边所在直线相交于E、F两点.过E作EG⊥DE交直线AB于G,连结DG.
(1)求BC的长;
(2)若E与B不重合,问t为何值时,△BEG与△DEG相似?
(3)试问:当t在什么范围内时,点G在线段BA的延长线上?当t在什么范围内时,点G在线段AB的延长线上?
(4)当点G在线段AB上(不包括端点A、B)时,求四边形ADEG的面积S(cm2)关于O点运动时间t(秒)的函数关系式,并问点O运动了几秒时,S取得最大值?最大值为多少?
第一轮复习教学案 圆(3)
【知识梳理】
1.各边 ,并且各角 的多边形是正多边形。
2.任一个正多边形都有一个外接圆和一个内切圆,它们是 圆。
3. 所有的正多边形都是轴对称图形,当正多边形的边数n为 时,
它也是 。
4.弧长公式为 ;扇形面积公式为 。
5.圆锥:
(1)侧面展开图:圆锥的侧面展开图是一个 形,这个扇形的半径是圆锥的 ,扇形的弧长是圆锥的 。
(2)圆锥的侧面积和全面积公式:设圆锥底面圆的半径为r,母线长为l,则S圆锥侧= ,S圆锥全= 。
【典型例题】
例1:(2007山东临沂)如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(1)求此圆的半径;(2)求图中阴影部分的面积。
例2:如图,在矩形ABCD中,AD=2,以B为圆心,BC长为半径画弧交AD于F.(1)若CF长为π,求圆心角∠CBF的度数;
(2)求图中阴影部分的面积(结果保留根号及π的形式).
例3: 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
【当堂反馈】
1.一个圆锥的高为3,侧面展开图是半圆,则圆锥的侧面积是( )
(A)9 (B)18 (C)27 (D)39
2. (2007四川内江)如图(5),这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中为,长为8cm,长为12cm,则阴影部分的面积为( )
A. B. C. D.
3. (2007浙江金华)如图所示为一弯形管道,其中心线是一段圆弧.已知半径,,则管道的长度(即的长)为 cm.(结果保留)
4. (2007山东济宁)如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 。
5. 若一个扇形的面积是12π,它的弧长是4π,则它的半径是( )
A.3 B.4 C.5 D.6
6. 把一个正五边形绕它的中心旋转,至少旋转_____°,就能与原来的位置重合;把一个正多边形绕它的中心旋转40°后能与原来的位置重合,这个正多边形的边数至少是_________。
【中考聚焦】
1. 如图,在正方形铁皮上剪下一个圆形和扇形,使之恰好围城图6—2所示的一个圆锥模型。设圆的半径为r,扇形的半径为R,则圆的半径与扇形的半径之间的关系为( )
A、R=2r B、R=r C、R=3r D、R=4r
2. 如右图,一块含有30 角的直角三角形ABC,在
水平桌面上绕点C按顺时针方向旋转到 A’B’C’
的位置。若BC的长为15cm,那么顶点A从开始到
结束所经过的路径长为 ( )
A.cm B.cm C.cm D.cm
3. 如图,三个同心扇形的圆心角∠AOB为120°,半径OA为6 cm,C、D是的三等分点,则阴影部分的面积等于 cm2.
4. 如图,半径为2的两个等圆⊙,⊙外切于点A,O2C切⊙于点C,弦BC∥O1O2,连结AB、AC,则图中阴影部分的面积等于 。
5. 如图,扇形OAB的圆心角为90°,以OB为直径的半圆O1与半圆O2外切,且⊙O1与⊙O2都与扇形弧相内切。
⑴求半圆O1与半圆O2的面积比;
⑵若OB=2,求图中阴影部分的面积。
O
A
B
C
E
F
D
G
B
C
A
F
D
A
B
O
【知识梳理】
基本概念: 弧、弦、圆心角、圆周角
确定圆的条件:
基本性质 对称性:
1.圆 垂径定理:
圆心角、弧、弦的关系定理:
圆周角定理:同弧或等弧所对的圆心角是它所对的圆周角的
推论:(1)同弧或等弧所的圆周角
(2)90°的圆周角所对弦是 ,
2. 点与圆的位置关系:( d是指:_________________________________)
_____________;_____________;_____________;
【典型例题】
例1: 如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出弧AC与弧BD的数量关系,并给予证明.
例2:(1)如图1,OA、OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点:过点C作CD切⊙O于点D,连结AD交DC于点E.求证:CD=CE
(2)若将图1中的半径OB所在直线向上平行移动交OA于F,交⊙O于B’,其他条件不变(如图2),那么上述结论CD=CE还成立吗 为什么
(3)若将图1中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变(如图3),那么上述结论CD=CE还成立吗 为什么
(图1) (图2) (图3)
例3:在坐标平面内,半径为R的⊙O与x轴交于点D(1,0)、E(5,0),与y轴的正半轴相切于点A。点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线BP,作EH⊥BP于H。
⑴求圆心C的坐标及半径R的值;
⑵△POB和△PHE随点P的运动而变化,若它们全等,
求a的值;
⑶若给定a=6,试判定直线BP与⊙C的位置关系(要
求说明理由)。
【当堂反馈】
1.小红的衣服被一个铁钉划了一个呈直角三角形的一个洞,其中三角形两边长分别为1cm和2cm,若用同色圆形布将此洞全部覆盖,那么这个圆布的直径最小应等于 。
2. 在平面直角坐标系中,以P(2,1)为圆心,r为半径的圆与坐标轴恰好有三个公共点,则r的值为 .
3. 如图,△ABC的三个顶点都在⊙O上,∠ACB=40°,则
∠AOB=____,∠OAB=_____。
4.⊙O的半径为6㎝,OA、OB、OC的长分别为5㎝、6㎝、7㎝,则点A、B、C与⊙O的位置关系是:点A在⊙O_____,点B在⊙O_______。
5. 如图,方格纸上一圆经过(2,5)、(-2,2)、(2,-3,)、(6,2)四点,则该圆圆心的坐标为 ( )
A.(2,-1) B.(2,2) C.(2,1) D.(3,1)
6.已知:如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=130°,过D点的切线PD与直线AB交于P点,则∠ADP的度数为( )
A.40° B.45° C.50° D.65°
7.(2006年金华市)如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.(1)求sin∠BAC的值;(2)如果OE⊥AC,垂足为E,求OE的长;(3)求tan∠ADC的值.(结果保留根号)
【中考聚焦】
1.(长春市)如图1,BD为⊙O的直径,∠A=30°,则∠CBD的度数为( )
A.30° B.60° C.80° D.120°
(1) (2) (3)
2.(绵阳市)如图2,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( ) A.100° B.110° C.120° D.130°
3.(重庆市)如图3,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于( ) A.80° B.50° C.40° D.20°
4.(哈尔滨市)半径为6的圆中,圆心角α的余弦值为,则角α所对弦长等于( ) A.4 B.10 C.8 D.6
5. 若一个直角三角形的两边分别为6和8,则这个直角三角形外接圆直径是( )
A.8 B.10 C.5或4 D.10或8
6. 如图4,D为等腰三角形ABC底边BC上的任意一点,AD的延长线交△ABC的外接圆于点E,连接BE、CE,则图中相似 (4)
三角形共有( ) A. 8对 B. 6对 C. 4对 D. 2对
7.下列图形中,各边的中点一定在同一个圆上的是( )
A. 矩形 B. 平行四边形 C. 梯形 D. 对角线互相垂直的四边形
8.已知:⊿ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,
(1)如图1,当∠A为锐角时,连接BE,试判断∠BAC与∠CBE的关系,并证明你的结论;
(2)图1,中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图2,CA的延长线与⊙O相交于E,请问:∠BAC与∠CBE的关系是否与(1)中你所得出的关系相同?若相同加以证明;若不同,请说明理由。
第一轮复习教学案 圆(2)
【知识梳理】
1.直线与圆的位置关系:( d是指:_________________________________)
_____________;_____________;_____________;
2.两圆位置关系:( d是指:_________________________________)____________________;____________________;____________________;____________________;____________________;
3.圆与切线
(1)圆的切线的性质: ;
(2)圆的切线的判定方法:(从定义) ;
(从直线与圆的位置关系) ;
(从判定定理) 。
(3)三角形的内切圆的圆心是 的交点 ,叫做三角形的 。
三角形的外接圆的圆心是 的交点 ,叫做三角形的 。
【典型例题】
例1:如图,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC于点E。判断DE与AC的位置关系,并说明理由。
例2:如图,⊙O1、⊙O2、⊙O3两两相切,且O1O2 =2,O1O3 =4,O2O3 =4。求⊙O1、⊙O2、⊙O3的半径。
例3:如图1,已知AB是⊙O的直径,AB垂直于弦CD,垂足为M,弦AE与CD交于F,则有结论AD2=AE·AF成立(不要求证明).
(1)若将弦CD向下平移至与⊙O相切于B点时,如图2,则AE.AF是否等于AG2 如果不相等,请探求AE·AF等于哪两条线段的积 并给出证明.
(2)当CD继续向下平移至与⊙O相离时,如图3,在(1)中探求的结论是否还成立,并说明理由
【当堂反馈】
1. 已知两圆的圆心距O1O2为3,⊙O1的半径为1,⊙O2的半径为2,则⊙O1与⊙O2的位置关系为____________________.
2. 若过⊙O内一点M的最长的弦长为6cm,最短的弦长为4cm.则OM的长
为 。
3. 一圆锥的轴截面是等边三角形,则其侧面展开图的圆心角是 。
4.已知圆锥的侧面展开图的图心角是72°,它的侧面积为10πcm2,则该圆锥的全面积是 cm2.
5. 已知⊙O的半径为10 cm,如果一条直线和圆心O的距离为10 cm,那么这条直线和这个圆的位置关系为( )
A相离 B.相切 C.相交 D.相交或相切
6. 以O为圆心的两个同心圆的半径分别为11cm和9 cm,若⊙P与这两个圆都相切,则下列说法中正确的是( ).
(A)⊙P的半径可以为2cm
(B)⊙P的半径可以为10 cm
(C)符合条件的点P有无数个且P点运动的路线是曲线
(D)符合条件的⊙P有无数个且P点运动的路线是直线
7. 如图,将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙的切点为A、B,点P是桌子边缘上一点,则∠APB等于( )
A、30° B、45° C、60° D、不能确定
【中考聚焦】
1. 已知关于x的一元二次方程x2-2(R+r)x+d2=0有实数根,其中R、r分别为⊙O1、⊙O2的半径,d为两圆的圆心距,则⊙O1与⊙O2的位置关系是 ( )
A.外离 B.相交 C.相切 D.以上都不正确
2. 如两圆的圆心距等于4,两圆半径分别是R和r,且R、r是方程x2-5x+4=0的两根,则两圆位置关系是( )
A、内含 B、外切 C、相交 D、 外离
3. 设⊙O的半径是r,点O到直线L的距离是d,若⊙O与L至少有一个公共点,则r与d之间的关系是( )
A.d>r B. d=r C. d
A、1 B、 C、 D、
5.(2007山东临沂)如图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为( )。
A、 B、 C、 D、
6.如图,已知Rt△ABC中,∠B=900,∠A=600,AB=cm.点O从C点出发,沿CB以每秒1cm的速度向B点方向运动,运动到B点时运动停止.当点O运动了t秒(t>0)时,以O点为圆心的圆与边AC相切于点D,与BC边所在直线相交于E、F两点.过E作EG⊥DE交直线AB于G,连结DG.
(1)求BC的长;
(2)若E与B不重合,问t为何值时,△BEG与△DEG相似?
(3)试问:当t在什么范围内时,点G在线段BA的延长线上?当t在什么范围内时,点G在线段AB的延长线上?
(4)当点G在线段AB上(不包括端点A、B)时,求四边形ADEG的面积S(cm2)关于O点运动时间t(秒)的函数关系式,并问点O运动了几秒时,S取得最大值?最大值为多少?
第一轮复习教学案 圆(3)
【知识梳理】
1.各边 ,并且各角 的多边形是正多边形。
2.任一个正多边形都有一个外接圆和一个内切圆,它们是 圆。
3. 所有的正多边形都是轴对称图形,当正多边形的边数n为 时,
它也是 。
4.弧长公式为 ;扇形面积公式为 。
5.圆锥:
(1)侧面展开图:圆锥的侧面展开图是一个 形,这个扇形的半径是圆锥的 ,扇形的弧长是圆锥的 。
(2)圆锥的侧面积和全面积公式:设圆锥底面圆的半径为r,母线长为l,则S圆锥侧= ,S圆锥全= 。
【典型例题】
例1:(2007山东临沂)如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(1)求此圆的半径;(2)求图中阴影部分的面积。
例2:如图,在矩形ABCD中,AD=2,以B为圆心,BC长为半径画弧交AD于F.(1)若CF长为π,求圆心角∠CBF的度数;
(2)求图中阴影部分的面积(结果保留根号及π的形式).
例3: 如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
【当堂反馈】
1.一个圆锥的高为3,侧面展开图是半圆,则圆锥的侧面积是( )
(A)9 (B)18 (C)27 (D)39
2. (2007四川内江)如图(5),这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中为,长为8cm,长为12cm,则阴影部分的面积为( )
A. B. C. D.
3. (2007浙江金华)如图所示为一弯形管道,其中心线是一段圆弧.已知半径,,则管道的长度(即的长)为 cm.(结果保留)
4. (2007山东济宁)如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 。
5. 若一个扇形的面积是12π,它的弧长是4π,则它的半径是( )
A.3 B.4 C.5 D.6
6. 把一个正五边形绕它的中心旋转,至少旋转_____°,就能与原来的位置重合;把一个正多边形绕它的中心旋转40°后能与原来的位置重合,这个正多边形的边数至少是_________。
【中考聚焦】
1. 如图,在正方形铁皮上剪下一个圆形和扇形,使之恰好围城图6—2所示的一个圆锥模型。设圆的半径为r,扇形的半径为R,则圆的半径与扇形的半径之间的关系为( )
A、R=2r B、R=r C、R=3r D、R=4r
2. 如右图,一块含有30 角的直角三角形ABC,在
水平桌面上绕点C按顺时针方向旋转到 A’B’C’
的位置。若BC的长为15cm,那么顶点A从开始到
结束所经过的路径长为 ( )
A.cm B.cm C.cm D.cm
3. 如图,三个同心扇形的圆心角∠AOB为120°,半径OA为6 cm,C、D是的三等分点,则阴影部分的面积等于 cm2.
4. 如图,半径为2的两个等圆⊙,⊙外切于点A,O2C切⊙于点C,弦BC∥O1O2,连结AB、AC,则图中阴影部分的面积等于 。
5. 如图,扇形OAB的圆心角为90°,以OB为直径的半圆O1与半圆O2外切,且⊙O1与⊙O2都与扇形弧相内切。
⑴求半圆O1与半圆O2的面积比;
⑵若OB=2,求图中阴影部分的面积。
O
A
B
C
E
F
D
G
B
C
A
F
D
A
B
O
