4.1-4.5 练习(含答案)浙教版数学八年级下册
文档属性
| 名称 | 4.1-4.5 练习(含答案)浙教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 872.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 09:07:57 | ||
图片预览




文档简介
4.1-4.5 练习
一、选择题
1.下列图标中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
2.一个正多边形的内角和为,则这个正多边形的边数为( )
A.5 B.6 C.7 D.8
3.在平行四边形中,,则等于( )
A. B. C. D.
4.下列命题中,真命题是( )
A.一条对角线平分一组对角的四边形是平行四边形
B.两条对角线相等的四边形是平行四边形
C.一组对边平行,一组对边相等的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
5.在直角坐标系中,点和点关于原点成中心对称,则的值为( )
A. B. C. D.
6.如图,小华注意到跷跷板静止状态时,可以与地面构成一个,跷跷板中间的支撑杆垂直于地面(分别为的中点),若,则点距离地面的高度为( )
A. B. C. D.
7.综合实践课上,魏华画出,利用尺规作图找一点,使得四边形为平行四边形.以下是其作图过程.
在魏华的作法中,可直接判定四边形为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
8.如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(8,4),若直线经过点D(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线DE的表达式是( )
A.y=x-2 B.y=2x-4 C.y=x-1 D.y=3x-6
9.如图所示,在四边形中,,,,,E,F分别是边的中点,则的长为( )
A. B. C. D.
10.已知平行四边形的一组邻边长为2和3,且有一个内角为,,是平行四边形边上的两点,且将此平行四边形分成面积相等的两部分,则线段的长度取值范围是( )
A. B. C. D.
二、填空题
11.一个多边形的内角和是它的外角和的5倍,则这个多边形的边数为 。
12.如图,在四边形中,与相交于点O,,添加条件 ,可得四边形为平行四边形(只需添加一个条件)
13.如图,在正方形中,对角线与相交于点O,E为上的一点,且,F为的中点,若的周长为30,则的长为 .
14.在平面直角坐标系中,点,,,点D为平面直角坐标系中的点,以A、B、C、D为顶点的四边形为平行四边形,则点D的坐标 .
15.如图,在平行四边形中,,,,点E为的中点,将平行四边形沿折痕翻折,使点D落在点E处,则线段的长为 .
16.如图,在平面直角坐标系中,点A,B,C的坐标分别为,,.点M从坐标原点O出发,第一次跳跃到点,使得点与点O关于点A成中心对称;第二次跳跃到点,使得点与点关于点B成中心对称;第三次跳跃到点,使得点与点关于点C成中心对称;第四次跳跃到点,使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
三、解答题
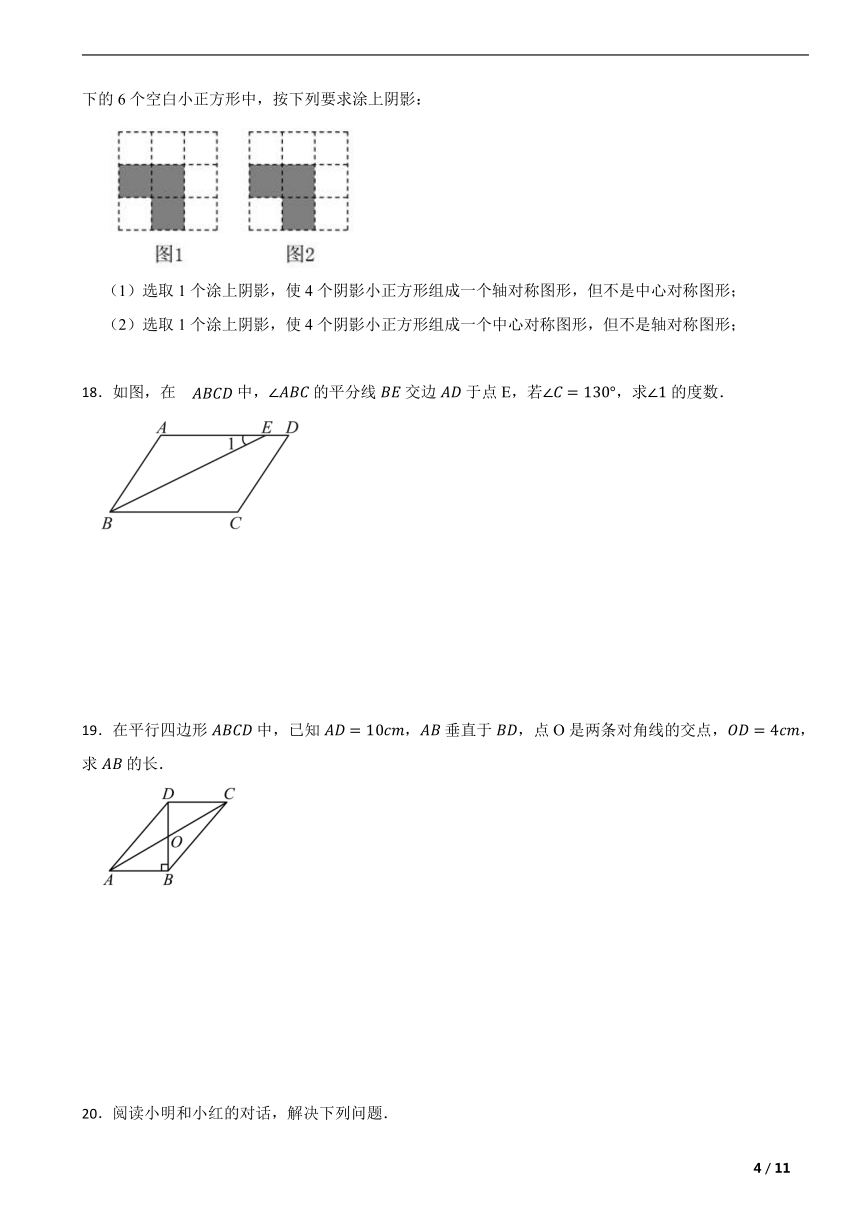
17.如图3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
18.如图,在中,的平分线交边于点E,若,求的度数.
19.在平行四边形中,已知,垂直于,点O是两条对角线的交点,,求的长.
20.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 度.
(2)若这是个正多边形,则这个正多边形的一个内角是多少度?
21.如图,在四边形中,.
(1)求的长;
(2)求四边形的面积.
22.如图所示,在中,点D,E分别为,的中点,点H在线段上,连接,点G,F分别为,的中点.
(1)求证:四边形为平行四边形;
(2)若,,,求的长.
23.如图,在直角坐标系中,四边形的顶点分别为:在边不与点重合,点在折线上运动,过点交边于点中点,连接.
(1)求证:四边形是平行四边形;
(2)当四边形是平行四边形时,求点的坐标;
(3)取线段的中点,作射线当射线经过点时,求的面积.
参考答案
1.B
2.B
3.D
4.D
5.D
6.B
7.B
8.A
9.A
10.C
11.12
12.
13.
14.或或
15.
16.
17.解:(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形,如下图所示:
;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形,如下图所示:
.
18.
19.
20(1)30
(2)150度
21.(1)
(2)
22.(1)证明:∵点D、E分别为AB,AC的中点
,,
∵点G、F分别为BH,CH的中点,
,
,
∴四边形DEFG为平行四边形
(2)解:四边形为平行四边形,
,
,
,
,
为中点,
即线段的长度为.
23.(1)证明:,,
轴,,
,,
,
,,
四边形是平行四边形;
(2)解:,,且,
是等腰三角形,
,
为中点,
,
当点在线段上时,
四边形是平行四边形,
,,
此时点的坐标为;
当点在线段上时,连接,
四边形是平行四边形,
,且,
为中点,,此时四边形是平行四边形,则轴,
,
设直线的解析式为,,
解得,
直线的解析式为,
当时,,解得,
点的坐标为;
综上,点的坐标为或;
(3)解:连接,根据题意得,线段的中点在线段上,连接,
,,
四边形是平行四边形,
为线段中点,点为线段的中点,
四边形是平行四边形,
,,
同理,直线的解析式为,
当时,,解得,
点的坐标为;
,
的面积.
1 / 1
一、选择题
1.下列图标中,既是中心对称图形,又是轴对称图形的是( )
A. B.
C. D.
2.一个正多边形的内角和为,则这个正多边形的边数为( )
A.5 B.6 C.7 D.8
3.在平行四边形中,,则等于( )
A. B. C. D.
4.下列命题中,真命题是( )
A.一条对角线平分一组对角的四边形是平行四边形
B.两条对角线相等的四边形是平行四边形
C.一组对边平行,一组对边相等的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
5.在直角坐标系中,点和点关于原点成中心对称,则的值为( )
A. B. C. D.
6.如图,小华注意到跷跷板静止状态时,可以与地面构成一个,跷跷板中间的支撑杆垂直于地面(分别为的中点),若,则点距离地面的高度为( )
A. B. C. D.
7.综合实践课上,魏华画出,利用尺规作图找一点,使得四边形为平行四边形.以下是其作图过程.
在魏华的作法中,可直接判定四边形为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
8.如图,在平面直角坐标系中,OABC的顶点A在x轴上,定点B的坐标为(8,4),若直线经过点D(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线DE的表达式是( )
A.y=x-2 B.y=2x-4 C.y=x-1 D.y=3x-6
9.如图所示,在四边形中,,,,,E,F分别是边的中点,则的长为( )
A. B. C. D.
10.已知平行四边形的一组邻边长为2和3,且有一个内角为,,是平行四边形边上的两点,且将此平行四边形分成面积相等的两部分,则线段的长度取值范围是( )
A. B. C. D.
二、填空题
11.一个多边形的内角和是它的外角和的5倍,则这个多边形的边数为 。
12.如图,在四边形中,与相交于点O,,添加条件 ,可得四边形为平行四边形(只需添加一个条件)
13.如图,在正方形中,对角线与相交于点O,E为上的一点,且,F为的中点,若的周长为30,则的长为 .
14.在平面直角坐标系中,点,,,点D为平面直角坐标系中的点,以A、B、C、D为顶点的四边形为平行四边形,则点D的坐标 .
15.如图,在平行四边形中,,,,点E为的中点,将平行四边形沿折痕翻折,使点D落在点E处,则线段的长为 .
16.如图,在平面直角坐标系中,点A,B,C的坐标分别为,,.点M从坐标原点O出发,第一次跳跃到点,使得点与点O关于点A成中心对称;第二次跳跃到点,使得点与点关于点B成中心对称;第三次跳跃到点,使得点与点关于点C成中心对称;第四次跳跃到点,使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
三、解答题
17.如图3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
18.如图,在中,的平分线交边于点E,若,求的度数.
19.在平行四边形中,已知,垂直于,点O是两条对角线的交点,,求的长.
20.阅读小明和小红的对话,解决下列问题.
(1)这个“多加的锐角”是 度.
(2)若这是个正多边形,则这个正多边形的一个内角是多少度?
21.如图,在四边形中,.
(1)求的长;
(2)求四边形的面积.
22.如图所示,在中,点D,E分别为,的中点,点H在线段上,连接,点G,F分别为,的中点.
(1)求证:四边形为平行四边形;
(2)若,,,求的长.
23.如图,在直角坐标系中,四边形的顶点分别为:在边不与点重合,点在折线上运动,过点交边于点中点,连接.
(1)求证:四边形是平行四边形;
(2)当四边形是平行四边形时,求点的坐标;
(3)取线段的中点,作射线当射线经过点时,求的面积.
参考答案
1.B
2.B
3.D
4.D
5.D
6.B
7.B
8.A
9.A
10.C
11.12
12.
13.
14.或或
15.
16.
17.解:(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形,如下图所示:
;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形,如下图所示:
.
18.
19.
20(1)30
(2)150度
21.(1)
(2)
22.(1)证明:∵点D、E分别为AB,AC的中点
,,
∵点G、F分别为BH,CH的中点,
,
,
∴四边形DEFG为平行四边形
(2)解:四边形为平行四边形,
,
,
,
,
为中点,
即线段的长度为.
23.(1)证明:,,
轴,,
,,
,
,,
四边形是平行四边形;
(2)解:,,且,
是等腰三角形,
,
为中点,
,
当点在线段上时,
四边形是平行四边形,
,,
此时点的坐标为;
当点在线段上时,连接,
四边形是平行四边形,
,且,
为中点,,此时四边形是平行四边形,则轴,
,
设直线的解析式为,,
解得,
直线的解析式为,
当时,,解得,
点的坐标为;
综上,点的坐标为或;
(3)解:连接,根据题意得,线段的中点在线段上,连接,
,,
四边形是平行四边形,
为线段中点,点为线段的中点,
四边形是平行四边形,
,,
同理,直线的解析式为,
当时,,解得,
点的坐标为;
,
的面积.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
