二次函数的性质

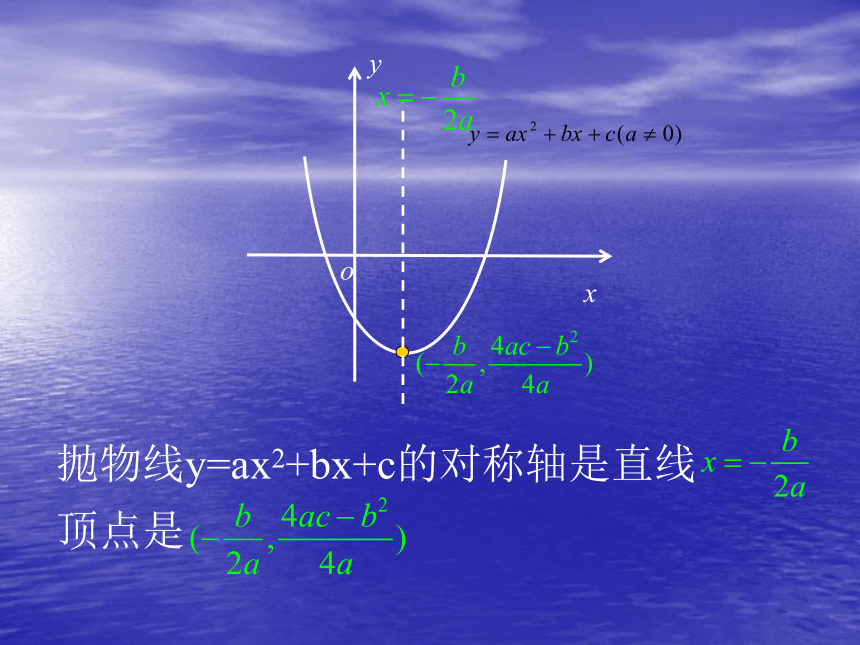
课件12张PPT。二次函数的性质初三数学抛物线y=ax2+bx+c的对称轴是直线 顶点是xyo(1)求抛物线y=ax2+bx+c的图象与y轴的交点?解：令x=0,则y=c.∴图象与y轴的交点坐标为(0,c)(2)求抛物线y=ax2+bx+c的图象与x轴的交点?解：令y=0,则ax2+bx+c=0；解得x=x1, x=x2 ∴图象与x轴的交点坐标为(x1,0);(x2 ,0)(x1,0)(x2 ,0)AB(0 ,c)C与X轴交点的横坐标x1,x2是一元二次方程ax2+bx+c=0的两根 △>0时，方程有两个不相等的实数解，
抛物线与X轴有两个交点△=0时，方程有两个相等的实数解，
抛物线与X轴只有一个交点△＜0时，方程没有实数解，抛物线与X轴
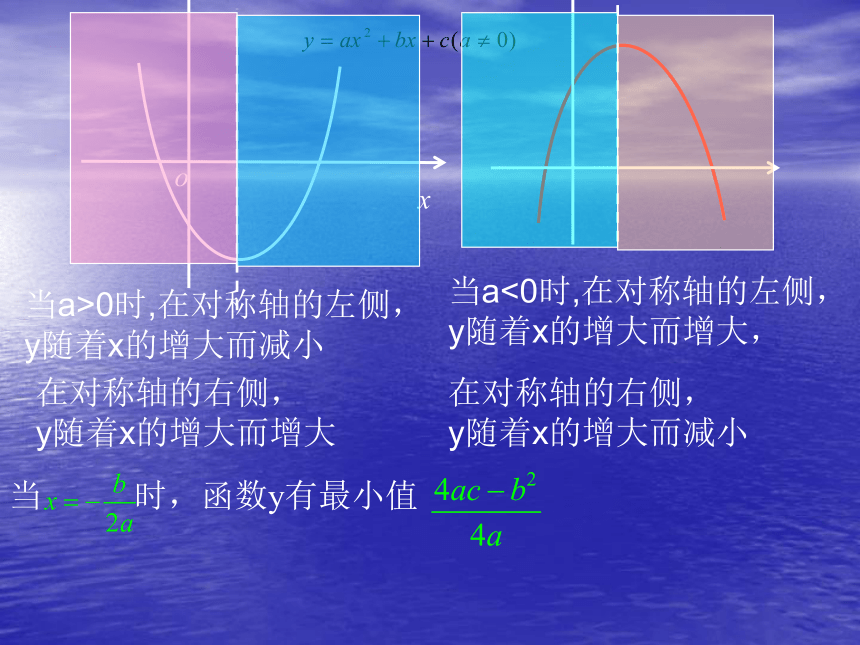
没有交点C‵当a>0时,在对称轴的左侧，y随着x的增大而减小 在对称轴的右侧，
y随着x的增大而增大 当a<0时,在对称轴的左侧，
y随着x的增大而增大， 在对称轴的右侧，
y随着x的增大而减小 当 时，函数y有最小值例：下列函数何时有最大值或最小值，并求出最大值或最小值。
(1)y=2x2-8x+1; (2)解：（1）∵y=2x2-8x+1=2(x-2)2-7 ∴顶点坐标为（2，-7）∴当x=2时，函数有最小值，Y最小值=-7 (2) ∵∴∴当x= 时，函数有最小值，Y最小值=∵a=-3 ∴函数有最大值例：已知函数
(1)写出函数图象的顶点、图象与坐标轴的交点，以及图象与Y轴的交点关于图象对称轴的对称点，然后画出函数图象的草图；
(2)根据上题的图象草图，写出X取哪些值时，
①y=0;②y<0;③y>0.
解:(1) ∵令y=0,即令x=0,y=解得x1, =－15，x2=1∴与x轴的交点是(-15,0),(1,0)∴∴图象顶点是（-7,32)∴与y轴的交点是(0, )∴这个交点关于对称轴x=-7的对称点是(-14， )-7当x=-15或x=1时，y=0;当x<-15或x>1时，图象在x轴的下方，y<0;当－154时，图象在x轴的下方，y<0;x1x2x1∵ x2>x1>1.5
在对称轴的右侧Ｙ随Ｘ的增大而增大x2X3∴Ｙ2>Ｙ1再见