浙教版八年级下册数学6.2.6反比例函数图像与性质(6) 课件(共26张PPT)
文档属性
| 名称 | 浙教版八年级下册数学6.2.6反比例函数图像与性质(6) 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
6.2.6 反比例函数图像与性质(6)
复习巩固
01
新课导入
02
课堂检测
03
延伸拓展
04
目
录
复习巩固
01
1、判断
A 一、二
B 二、三
C 一、三
D 二、四
1) 为反比例函数( )
2)反比例函数的图象是曲线,与x、y轴有 交点( )
3) 反比例函数的图象是中心对称图形 ( )
2、选择、填空
1)函数 过 ( )象限
2)反比例函数 当x=-3时y=-2,则k= 此时函数图象经过第 象限。
3)若函数 图象经过一、三 象限,则k的取值范
围是
错
错
对
D
6
一、三
K>1
小明在学习了反比例函数的图象与性质(1)后,与正比例函数y=kx (k ≠0) 的性质做了比较,他发现有一些相同,但又有一些现在不能比较,你能帮小明说说有哪些相同的,什么还不能比较呢?
相同:k>0时,都经过一、三象限;
k<0时,都经过二、四象限
暂不能比较的:k>0时正比例函数y随x的增大而增大;
k<0时正比例函数y随x的增大而减小。
那么反比例函数有没有这样的类似性质呢,你能不能帮小明解决这个问题呢?
新课导入
02
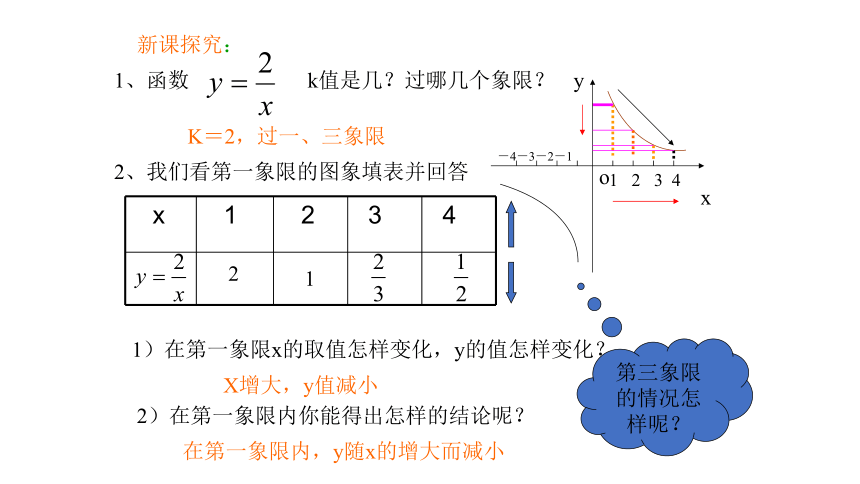
新课探究:
1、函数 k值是几?过哪几个象限?
2、我们看第一象限的图象填表并回答
x 1 2 3 4
1 2 3 4
x
y
o
-4-3-2-1
1)在第一象限x的取值怎样变化,y的值怎样变化?
2)在第一象限内你能得出怎样的结论呢?
第三象限的情况怎样呢?
2
1
K=2,过一、三象限
X增大,y值减小
在第一象限内,y随x的增大而减小
x
y
o
-4-3-2-1
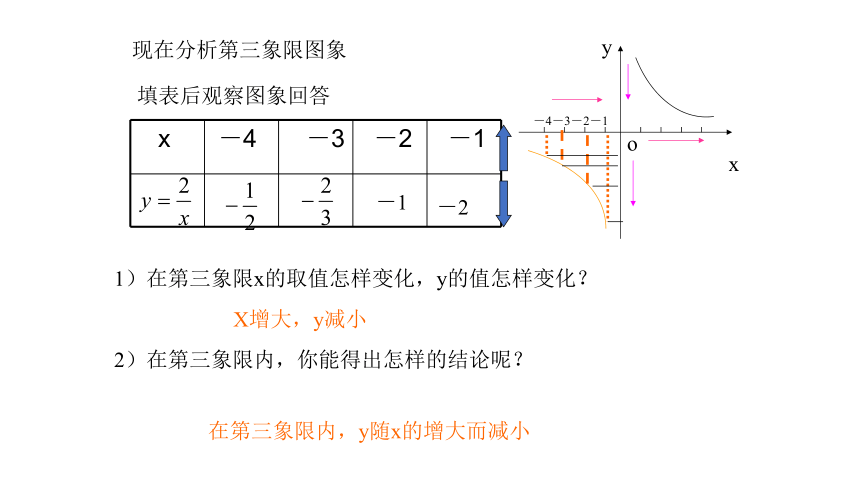
x -4 -3 -2 -1
现在分析第三象限图象
填表后观察图象回答
1)在第三象限x的取值怎样变化,y的值怎样变化?
2)在第三象限内,你能得出怎样的结论呢?
-1
-2
X增大,y减小
在第三象限内,y随x的增大而减小
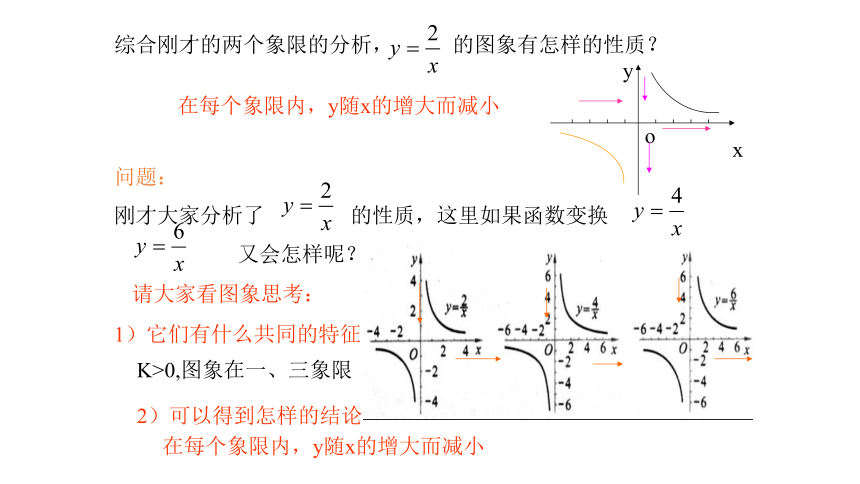
综合刚才的两个象限的分析, 的图象有怎样的性质?
问题:
刚才大家分析了 的性质,这里如果函数变换
又会怎样呢?
请大家看图象思考:
1)它们有什么共同的特征
2)可以得到怎样的结论
在每个象限内,y随x的增大而减小
K>0,图象在一、三象限
在每个象限内,y随x的增大而减小
x
y
o
从 这几个函数你能总
结出怎样的性质?
反比例函数 的图象,当k>0时,在每一象
限内,y的值随x的增大而减小。
刚刚我们总结了k>0时的反比例函数的性质,那么k<0的时候
又会怎样呢?
请同学们按照刚才的方法分组进行探究
探究的结论:请同学们回答
当k<0时,在每一象限内,y的值随x的增大而增大。
分组探究
综合我们的探讨可以得到怎样的性质呢?
反比例函数的图象,
当k>0时,在每一象限内,y的值随x值的增大而减小;
当k<0时,在每一象限内,y的值随x的增大而增大。
课堂检测
03
巩固训练一
一、判断
1) 在每一象限内 ,y随x的增大而减小 ( )
2) 在每一象限内, y随x的增大而增大 ( )
二、
2)反比例函数 ,当x=1时,y=2,则k= , y随x的
减小而
错
错
2
增大
象限,
Y随x的增大而
(注意:做题时审清题目的问法)
3) 若反比例函数 在每一象限内,y随x的增大而
增大,则它的图象经过一、三象限
( )
错
二、四
增大
3)反比例函数 的图象上有两点A(1,y1),B(2,y2),
则y1-y2的值是( )
A 正数 B负数 C非正数 D不能确定
训练二
1)反比例函数 ,当x=1时,y=2,则k= , y随x的
增大而
2 )已知反比例函数 , 那么y的值随x的增大而( )
A 不变 B增大 C减小 D不确定
1
减小
C
A
4)反比例函数 的图象上有两点A(x1,y1),B(x2,y2),且
X1A 正数 B负数 C非正数 D不能确定
x
y
o
本题要注意A,B是否在同一象限内
若A,B在不同的象限则可能有多种情况出现
D
数学题目形式灵活多变,大家要善于思考
小明在学完反比例函数性质后做课外练习时又遇到了它百思不得其解的题目,你能帮他解决吗?
x
y
o
P
F
E
已知P(2, )为反比例函数
图象上第一象限的点,过P分别作x轴、y轴的平行线PE、PF,与坐标轴围成的矩形PEOF的面积为多少?
分析:解这道题关键要弄清长、宽
解:依题意得 PE=2 , PF=
S矩形PEOF =PE×PF=2× =1
B
结果一样,注意点在第三象限,求解的过程中要长宽加绝对值
若点B(-3, )点C ( 4, )同样方法构造矩形,结果会怎样吗?
C
如果题目再变化一下,大家思考一下又该怎样解?
已知点 P 为反比例函数
上的点,过P分别作x轴、y轴的平行线PE、PF,与坐标轴围成的矩形PEOF的面积为多少?
x
y
o
P
E
F
分析:要解这题,关键表达出长、宽即要求PE、PF
你能从本题得到什么启发吗
无论点在图象上的何位置所围成的矩形面积都是定值
P
Q
S1
S2
S1、S2有什么关系?
R
S3
想一想
S3
S1、S2有什么关系?
相等
相等
遇到一些较复杂的问题常常可以把问题分解,在探究。
如右图,点A在反比例函数 的图象上,且点A的横坐标分别为1,AC⊥x轴,垂足为点C,且△AOC的面积为2。
(1)求该反比例函数的解析式。
(2)若点(-1,y1),(-2,y2)在该反比例函数 的图象上, 试比较y1与y2的大小。
综合演练
分析:要求解析式和第二问,关键是求K的值,而S△AOC=2这个条件,给了我们一个求解的桥梁.如果可以表示出来AC,OC,而要表示这两边,则需要设出点A的坐标,然后求解K
求出K值第二问就可利用性质去求解.
x
y
o
C
A
如右图,点A在反比例函数 的图象上,且点A的横坐标分别为1,AC⊥x轴,垂足为点C,且△AOC的面积为2。
(1)求该反比例函数的解析式。
(2)若点(-1,y1),(-2,y2)在该反比例函数 的图象上, 试比较y1与y2的大小。
综合演练
x
y
o
C
A
如右图,点A在反比例函数 的图象上,且点A的横坐标分别为1,AC⊥x轴,垂足为点C,且△AOC的面积为2。
(1)求该反比例函数的解析式。
(2)若点(-1,y1),(-2,y2)在该反比例函数 的图象上, 试比较y1与y2的大小。
综合演练
x
y
o
C
A
延伸拓展
04
请在座的同学小结一下本节课学习的内容。
1、进一步学习了反比例函数图象的性质。
反比例函数的图象,当k>0时,在每一象限内, y随x的增大而减小;当k<0时,在每一象限内,y随x的增大而增大。
2、探究与反比例函数相关的综合题型
3、学习新知识时要善于运用类比的思想方法进行比较学习,要善于用数形结合的思想方法解题。
4、希望这节课后大家对数学问题多思考和探究,培养自己善于思考、善于钻研的精神。
作业:
在直角坐标系中,直线 与双曲线 在
第一象限交于点A,与x轴交于点C,AB⊥ x轴,垂足为
B,且 。(1)求m的值(2)求△ABC的面积
6.2.6 反比例函数图像与性质(6)
6.2.6 反比例函数图像与性质(6)
复习巩固
01
新课导入
02
课堂检测
03
延伸拓展
04
目
录
复习巩固
01
1、判断
A 一、二
B 二、三
C 一、三
D 二、四
1) 为反比例函数( )
2)反比例函数的图象是曲线,与x、y轴有 交点( )
3) 反比例函数的图象是中心对称图形 ( )
2、选择、填空
1)函数 过 ( )象限
2)反比例函数 当x=-3时y=-2,则k= 此时函数图象经过第 象限。
3)若函数 图象经过一、三 象限,则k的取值范
围是
错
错
对
D
6
一、三
K>1
小明在学习了反比例函数的图象与性质(1)后,与正比例函数y=kx (k ≠0) 的性质做了比较,他发现有一些相同,但又有一些现在不能比较,你能帮小明说说有哪些相同的,什么还不能比较呢?
相同:k>0时,都经过一、三象限;
k<0时,都经过二、四象限
暂不能比较的:k>0时正比例函数y随x的增大而增大;
k<0时正比例函数y随x的增大而减小。
那么反比例函数有没有这样的类似性质呢,你能不能帮小明解决这个问题呢?
新课导入
02
新课探究:
1、函数 k值是几?过哪几个象限?
2、我们看第一象限的图象填表并回答
x 1 2 3 4
1 2 3 4
x
y
o
-4-3-2-1
1)在第一象限x的取值怎样变化,y的值怎样变化?
2)在第一象限内你能得出怎样的结论呢?
第三象限的情况怎样呢?
2
1
K=2,过一、三象限
X增大,y值减小
在第一象限内,y随x的增大而减小
x
y
o
-4-3-2-1
x -4 -3 -2 -1
现在分析第三象限图象
填表后观察图象回答
1)在第三象限x的取值怎样变化,y的值怎样变化?
2)在第三象限内,你能得出怎样的结论呢?
-1
-2
X增大,y减小
在第三象限内,y随x的增大而减小
综合刚才的两个象限的分析, 的图象有怎样的性质?
问题:
刚才大家分析了 的性质,这里如果函数变换
又会怎样呢?
请大家看图象思考:
1)它们有什么共同的特征
2)可以得到怎样的结论
在每个象限内,y随x的增大而减小
K>0,图象在一、三象限
在每个象限内,y随x的增大而减小
x
y
o
从 这几个函数你能总
结出怎样的性质?
反比例函数 的图象,当k>0时,在每一象
限内,y的值随x的增大而减小。
刚刚我们总结了k>0时的反比例函数的性质,那么k<0的时候
又会怎样呢?
请同学们按照刚才的方法分组进行探究
探究的结论:请同学们回答
当k<0时,在每一象限内,y的值随x的增大而增大。
分组探究
综合我们的探讨可以得到怎样的性质呢?
反比例函数的图象,
当k>0时,在每一象限内,y的值随x值的增大而减小;
当k<0时,在每一象限内,y的值随x的增大而增大。
课堂检测
03
巩固训练一
一、判断
1) 在每一象限内 ,y随x的增大而减小 ( )
2) 在每一象限内, y随x的增大而增大 ( )
二、
2)反比例函数 ,当x=1时,y=2,则k= , y随x的
减小而
错
错
2
增大
象限,
Y随x的增大而
(注意:做题时审清题目的问法)
3) 若反比例函数 在每一象限内,y随x的增大而
增大,则它的图象经过一、三象限
( )
错
二、四
增大
3)反比例函数 的图象上有两点A(1,y1),B(2,y2),
则y1-y2的值是( )
A 正数 B负数 C非正数 D不能确定
训练二
1)反比例函数 ,当x=1时,y=2,则k= , y随x的
增大而
2 )已知反比例函数 , 那么y的值随x的增大而( )
A 不变 B增大 C减小 D不确定
1
减小
C
A
4)反比例函数 的图象上有两点A(x1,y1),B(x2,y2),且
X1
x
y
o
本题要注意A,B是否在同一象限内
若A,B在不同的象限则可能有多种情况出现
D
数学题目形式灵活多变,大家要善于思考
小明在学完反比例函数性质后做课外练习时又遇到了它百思不得其解的题目,你能帮他解决吗?
x
y
o
P
F
E
已知P(2, )为反比例函数
图象上第一象限的点,过P分别作x轴、y轴的平行线PE、PF,与坐标轴围成的矩形PEOF的面积为多少?
分析:解这道题关键要弄清长、宽
解:依题意得 PE=2 , PF=
S矩形PEOF =PE×PF=2× =1
B
结果一样,注意点在第三象限,求解的过程中要长宽加绝对值
若点B(-3, )点C ( 4, )同样方法构造矩形,结果会怎样吗?
C
如果题目再变化一下,大家思考一下又该怎样解?
已知点 P 为反比例函数
上的点,过P分别作x轴、y轴的平行线PE、PF,与坐标轴围成的矩形PEOF的面积为多少?
x
y
o
P
E
F
分析:要解这题,关键表达出长、宽即要求PE、PF
你能从本题得到什么启发吗
无论点在图象上的何位置所围成的矩形面积都是定值
P
Q
S1
S2
S1、S2有什么关系?
R
S3
想一想
S3
S1、S2有什么关系?
相等
相等
遇到一些较复杂的问题常常可以把问题分解,在探究。
如右图,点A在反比例函数 的图象上,且点A的横坐标分别为1,AC⊥x轴,垂足为点C,且△AOC的面积为2。
(1)求该反比例函数的解析式。
(2)若点(-1,y1),(-2,y2)在该反比例函数 的图象上, 试比较y1与y2的大小。
综合演练
分析:要求解析式和第二问,关键是求K的值,而S△AOC=2这个条件,给了我们一个求解的桥梁.如果可以表示出来AC,OC,而要表示这两边,则需要设出点A的坐标,然后求解K
求出K值第二问就可利用性质去求解.
x
y
o
C
A
如右图,点A在反比例函数 的图象上,且点A的横坐标分别为1,AC⊥x轴,垂足为点C,且△AOC的面积为2。
(1)求该反比例函数的解析式。
(2)若点(-1,y1),(-2,y2)在该反比例函数 的图象上, 试比较y1与y2的大小。
综合演练
x
y
o
C
A
如右图,点A在反比例函数 的图象上,且点A的横坐标分别为1,AC⊥x轴,垂足为点C,且△AOC的面积为2。
(1)求该反比例函数的解析式。
(2)若点(-1,y1),(-2,y2)在该反比例函数 的图象上, 试比较y1与y2的大小。
综合演练
x
y
o
C
A
延伸拓展
04
请在座的同学小结一下本节课学习的内容。
1、进一步学习了反比例函数图象的性质。
反比例函数的图象,当k>0时,在每一象限内, y随x的增大而减小;当k<0时,在每一象限内,y随x的增大而增大。
2、探究与反比例函数相关的综合题型
3、学习新知识时要善于运用类比的思想方法进行比较学习,要善于用数形结合的思想方法解题。
4、希望这节课后大家对数学问题多思考和探究,培养自己善于思考、善于钻研的精神。
作业:
在直角坐标系中,直线 与双曲线 在
第一象限交于点A,与x轴交于点C,AB⊥ x轴,垂足为
B,且 。(1)求m的值(2)求△ABC的面积
6.2.6 反比例函数图像与性质(6)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
