1.1二次根式

课件24张PPT。1.1 二次根式(2) 3的算术平方根是_______ 以前学的知识还记得吗？（3） 有意义吗？为什么？ （4)一个非负数a的算术平方根应表示为__________（1） 3的平方根是______算术平方根的性质：正数和0都有算术平方根；
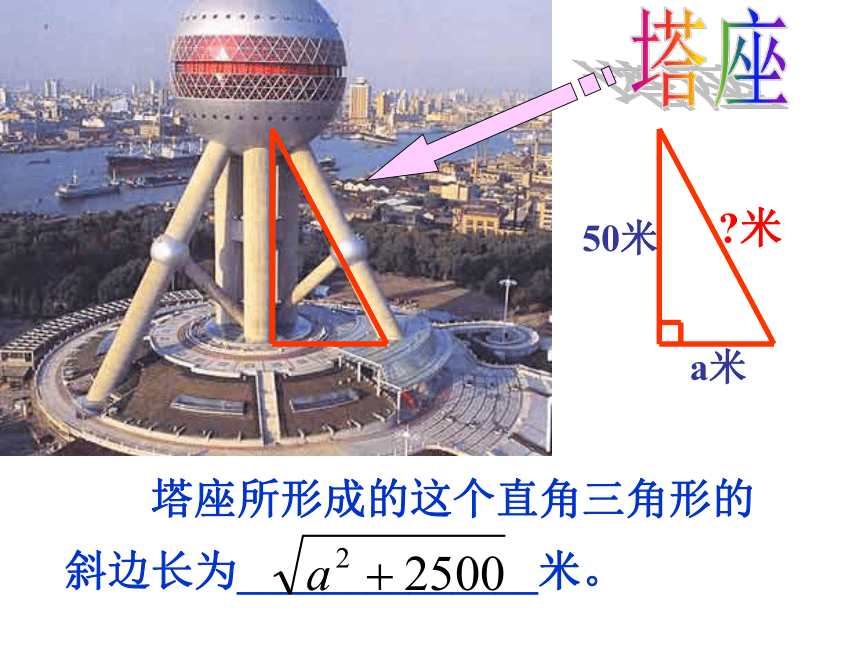
负数没有算术平方根。温故而知新50米a米 塔座所形成的这个直角三角形的
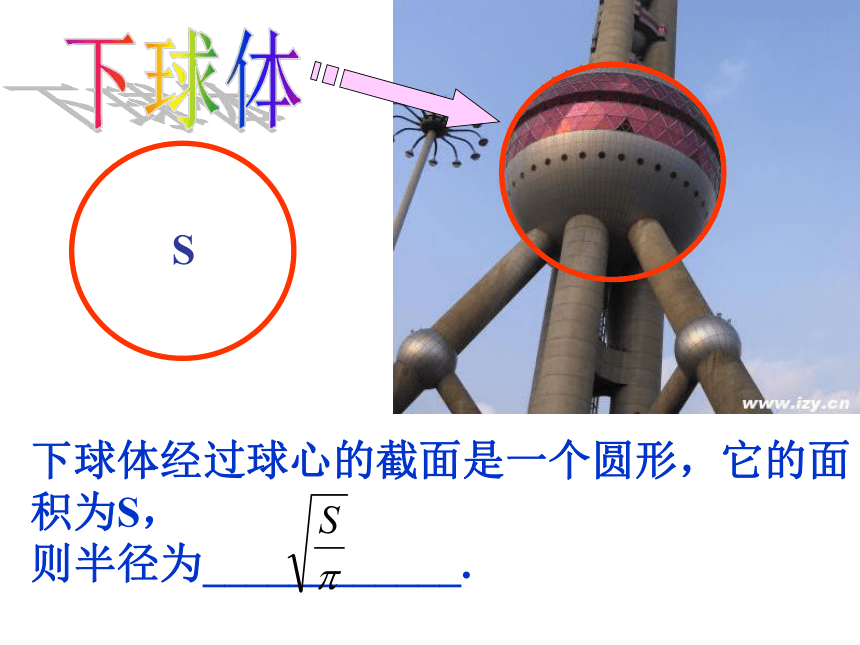
斜边长为______________米。塔座?米下球体S 下球体经过球心的截面是一个圆形，它的面积为S，
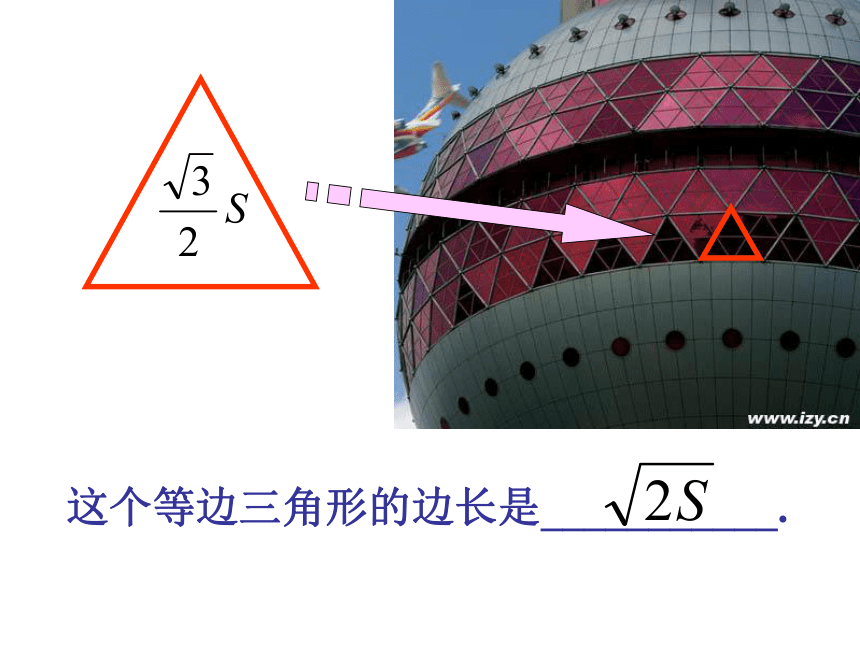
则半径为____________.这个等边三角形的边长是___________.这些代数式有什么共同的特点？ 像 ， ， 这样表
示的算术平方根，且二次根号内含有字母的代数式叫做二次根式。 为了方便起见，我们把一个数的算术平
方根（如 ， ）也叫二次根式。如： 这类代数式只能称为含有二次根式的代数式，不能称之为二次根式；
而
这类代数式，应把 这些二次根式看做系数或常数项，整个代数式仍看做整式。注意1、判断：下列各式中那些是二次根式？二次根式根号内字母的取值范围必须满足:
被开方数大于或等于零例1 求下列二次根式中字母的取值范围：求二次根式中字母的取值范围的基本依据：①被开方数大于或等于零；②分母中有字母时，要保证分母不为零。(5)比一比还记得怎样求代数式的值吗？例2. 当 x = –4时，求二次根式 的值。若二次根式 的值为3，求x的值.变形练习若二次根式 的值为3，求x的值。解：
由题意得:
两边同时平方得:小试牛刀:例3 一艘轮船先向东北方向航行2小时，再向
西北方向航行t小时。船的航速是每时25千米。
1、用关于t的代数式表示船离开出发地的距离。
2、求当t=3时，船离开出发地多少千米。
（精确到头0.01千米）东北 轮船ACB 从东方明珠塔顶上自由落下一个物体，其下落的距离h（米）可用公式 来估计，其中t（秒）表示物体下落所经过的时间。（1）把这个公式变形成用h表示t的公式；（2）东方明珠塔高468米，则该物体落到塔底需几秒？（精确到0.01秒）你掌握今天的重点内容了吗？ 3. 分类讨论思想一个概念：二次根式
两类题型：1. 求代数式所含字母的取值范围

2. 求二次根式的值
三点注意：1. 二次根式的双重非负性

2. 分母不能为0 形如 的代数式 列不等式（组） 归纳小结：一个概念（二次根式）:（1） 求二次根式中字母的取值范围（2） 求二次根式的值①被开方数不小于零；②分母中有字母时，要保证分母不为零。两类题型： 形如 的代数式切入点：从字母的取值范围入手。1.已知 ，你能求出 的值吗？3.已知 ，你能求出 的取值范围吗？2.已知 与 互为相反数，
求 、 的值.探索与交流——提升我们的数学思维能力切入点：从代数式的非负性入手。4.已知 为一个非负整数，试求非负整数 的值切入点：分类讨论思想。想一想：甲、乙两人计算当a = - 1.5时 a - 的值。 得到下列两种不同的答案，哪个正确？甲的解答是 a - = a -（a+1）= -1；乙的解答是 a - = a +（a+1）=2a+1=2×（-1.5)+1= - 2延伸与提高求出下列二次根式中字母a的取值范围：因为难,所以我挑战!1. 求式子 有意义时X的取值范围。
解:由题意得,已知 有意义,那A(a, )
在 象限.二 ?试试你的反应∵由题意知a＜0∴点A(－,＋)知识纵横 ?若a.b为实数,且求 的值。解:


知识纵横