新浙教版数学八年级(下)单元测验 第五章 特殊平行四边形基础能力测试卷(含参考答案)
文档属性
| 名称 | 新浙教版数学八年级(下)单元测验 第五章 特殊平行四边形基础能力测试卷(含参考答案) |  | |
| 格式 | zip | ||
| 文件大小 | 557.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-30 13:48:12 | ||
图片预览



文档简介
第五章 特殊平行四边形基础能力测试卷
班级 姓名 学号
一、选择题(共10小题,每小题3分,满分30分)
1、如图,在菱形中,,∠,则对角线等于( )
A.20 B.15 C.10 D.5
2、下列命题是真命题的是( )
A. 一组对边平行,另一组对边相等的四边形是平行四边形
B. 对角线互相垂直的平行四边形是矩形
C. 四条边相等的四边形是菱形
D. 正方形是轴对称图形,但不是中心对称图形
3、已知四边形ABCD是平行四边形,若要使它成为正方形,则应增加的条件是
( )
A. AC⊥BD B.AC=BD C.AC=BD且AC⊥BD D. AC平分∠BAD
4、如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=,BD=4,则菱形ABCD的周长为( )
A. 4 B. 4 C. 4 D.28
5、已知,在等腰△ABC中,AB=AC,分别延长BA,CA到D,E点,使DA=AB,EA=CA,则四边形BCDE是( )2·1·c·n·j·y
A. 任意四边形 B.矩形 C.菱形 D. 正方形
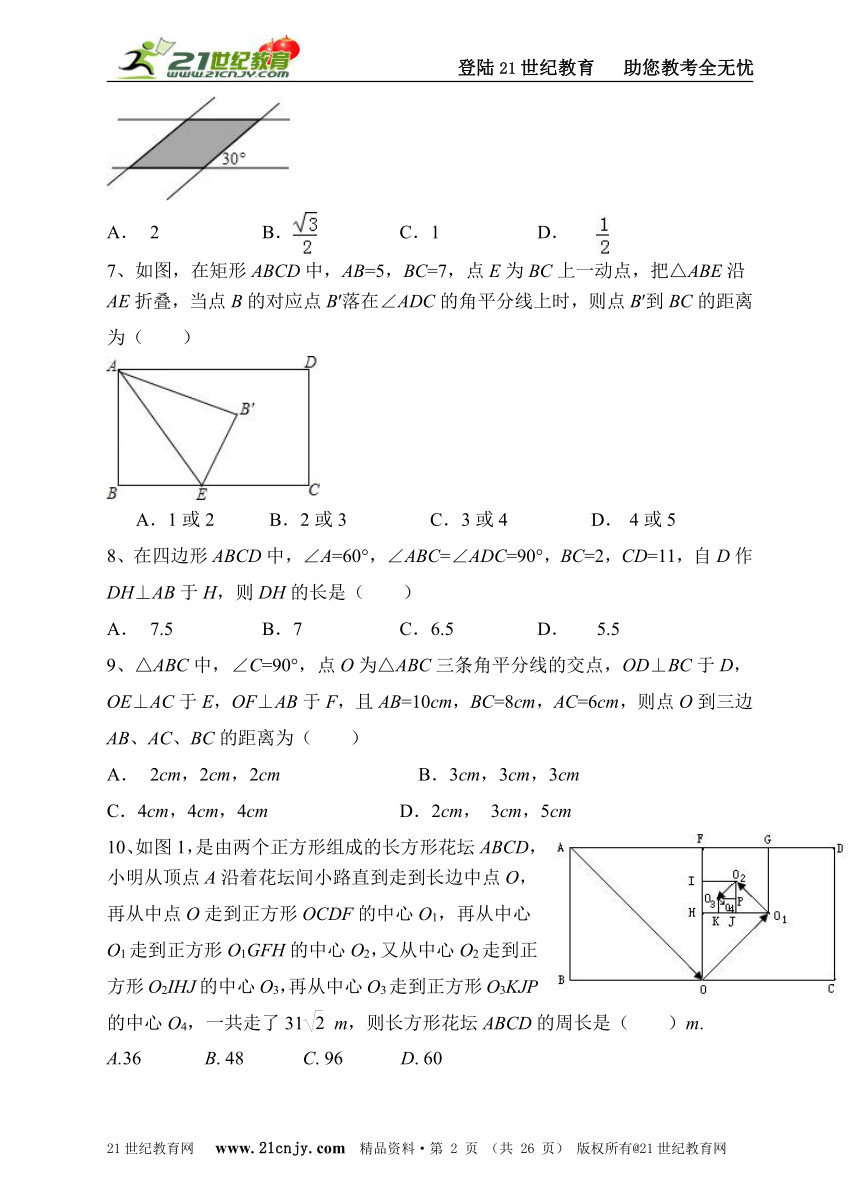
6、如图,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)
的面积是( )
A. 2 B. C.1 D.
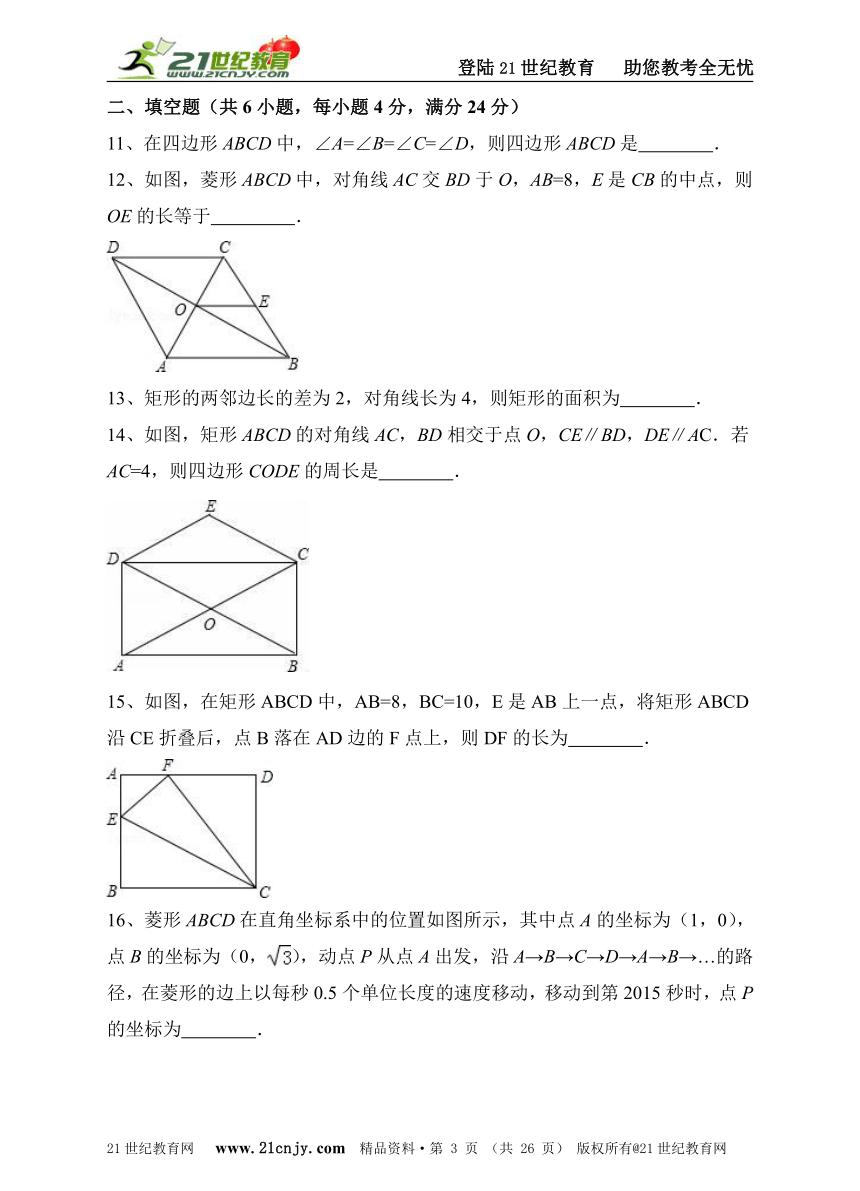
7、如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿
AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )
A.1或2 B.2或3 C.3或4 D. 4或5
8、在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,自D作DH⊥AB于H,则DH的长是( )www-2-1-cnjy-com
A. 7.5 B.7 C.6.5 D. 5.5
9、△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )【来源:21cnj*y.co*m】
A. 2cm,2cm,2cm B.3cm,3cm,3cm
C.4cm,4cm,4cm D.2cm, 3cm,5cm
10、如图1,是由两个正方形组成的长方形花坛ABCD,
小明从顶点A沿着花坛间小路直到走到长边中点O,
再从中点O走到正方形OCDF的中心O1,再从中心
O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走到正方形O3KJP
的中心O4,一共走了31m,则长方形花坛ABCD的周长是( )m.
A.36 B. 48 C. 96 D. 60
二、填空题(共6小题,每小题4分,满分24分)
11、在四边形ABCD中,∠A=∠B=∠C=∠D,则四边形ABCD是 .
12、如图,菱形ABCD中,对角线AC交BD于O,AB=8,E是CB的中点,则OE的长等于 .
13、矩形的两邻边长的差为2,对角线长为4,则矩形的面积为 .
14、如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是 .
15、如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 .
16、菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2015秒时,点P的坐标为 .21cnjy.com
三、解答题(本题有7个小题,共66分)解答应写出证明过程或推演步骤.
17、(6分)如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,选择的条件是 (只填写序号).
18、(8分)为美化环境,某单位需要在一块正方形空地上分别种植四种不同的花草,计划将这块空地按如下要求分成四块:⑴分割后的整个图形必须是中心对称图形;⑵四块图形的形状相同;⑶四块图形的面积相等.
请按照上述三个要求,分别在下面的正方形中给出4种不同的分割方法.
(尺规或徒手作图均可,但要尽可能准确、美观些,不写画法)
19、(8分)在平面直角坐标系xoy中 ,直线y=-x+3 与x轴、y轴分别教育A、B ,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标。
20、(10分)如图1,纸片□ABCD中,AD=5,S□ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
21、(10分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=6,BC=8,求MD的长.
22、(12分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.21教育网
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
23、(12分)如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)【出处:21教育名师】
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
答案详解
一、选择题(共10小题,每小题3分,满分30分)
【解答】 解:
A、一组对边平行,且相等的四边形是平行四边形,所以A选项错误;
B、对角线互相垂直,且相等的平行四边形是矩形,所以B选项错误;
C、四条边相等的四边形是菱形,所以C选项正确;
D、正方形是轴对称图形,也是中心对称图形,所以D选项错误.
故选C.
3、已知四边形ABCD是平行四边形,若要使它成为正方形,则应增加的条件是( )
A. AC⊥BD B.AC=BD C.AC=BD且AC⊥BD D. AC平分∠BAD
【解答】 解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,故错误;
B、∵四边形ABCD是平行四边形,AC=BD,
∴四边形ABCD是矩形,故错误;
C、∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
∵AC=BD, ∴四边形ABCD是正方形,故正确;
D、∵四边形ABCD是平行四边形,AC平分∠BAD,
∴四边形ABCD是矩形,故错误.
故选C.
4、如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=,BD=4,则菱形ABCD的周长为( )
A. 4 B. 4 C. 4 D.28
【解答】 解:∵E,F分别是AB,BC边上的中点,EF=,
∴AC=2EF=2,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=,OB=BD=2,
∴AB==,
∴菱形ABCD的周长为4.
故选:C.
5、已知,在等腰△ABC中,AB=AC,分别延长BA,CA到D,E点,使DA=AB,EA=CA,则四边形BCDE是( )21教育名师原创作品
A. 任意四边形 B.矩形 C.菱形 D. 正方形
【解答】 解:如图所示,
∵AC=AE,AB=AD
∴四边形BCDE为平行四边形,
∵AB=AE,∴∠AEB=∠ABE,
∵∠BAC+∠ABC+∠ACB=180°
∠ABC=∠ACB
∴∠ABC+∠EBA=90°
∴四边形BCDE为矩形.
故选B.
6、如图,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( )
A. 2 B. C.1 D.
【解答】 解:因为在直角三角形中30度角对应的直角边是斜边的一半,
在题目中的菱形中,已知菱形的高为1,可得边长为2,
所以面积为2.
故选:A.
7、如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )21*cnjy*com
A.1或2 B.2或3 C.3或4 D. 4或5
【解答】 解:如图,连接B′D,过点B′作B′M⊥AD于M.
∵点B的对应点B′落在∠ADC的角平分线上,
∴设DM=B′M=x,则AM=7﹣x,
又由折叠的性质知AB=AB′=5,
∴在直角△AMB′中,由勾股定理得到:AM2=AB′2﹣B′M2
即(7﹣x)2=25﹣x2,
解得x=3或x=4,
则点B′到BC的距离为2或1.
故选:A.
8、在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,自D作DH⊥AB于H,则DH的长是( )【版权所有:21教育】
A. 7.5 B.7 C.6.5 D. 5.5
【解答】 解:过C作DH的垂线CE交DH于E,
∵DH⊥AB,CB⊥AB,
∴CB∥DH又CE⊥DH,
∴四边形BCEH是矩形.
∵HE=BC=2,在Rt△AHD中,∠A=60°,
∴∠ADH=30°,
又∵∠ADC=90°
∴∠CDE=60°,
∴∠DCE=30°,
∴在Rt△CED中,DE=CD=5.5,
∴DH=2+5.5=7.5.
故选A.
9、△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A. 2cm,2cm,2cm B.3cm,3cm,3cm
C.4cm,4cm,4cm D.2cm, 3cm,5cm
【解答】 解:解答:解:连接OA,OB,OC,则△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,21·世纪*教育网
∴BD=BF,CD=CE,AE=AF,
又∵∠C=90,OD⊥BC于D,OE⊥AC于E,且O为△ABC三条角平分线的交点
∴四边形OECD是正方形,
则点O到三边AB、AC、BC的距离=CD,
∴AB=8﹣CD+6﹣CD=﹣2CD+14,又根据勾股定理可得:AB=10,
即﹣2CD+14=10
∴CD=2,
即点O到三边AB、AC、BC的距离为2cm.
故选A
10、如图1,是由两个正方形组成的长方形花坛ABCD,
小明从顶点A沿着花坛间小路直到走到长边中点O,
再从中点O走到正方形OCDF的中心O1,再从中心
O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走到正方形O3KJP
的中心O4,一共走了31m,则长方形花坛ABCD的周长是( )m.
A.36 B. 48 C. 96 D. 60
【解答】 解:设AB=BO=a,根据勾股定理,得AO=a,
所以001=,O1O2=,0203=,0304=.
由A0+001+0102+0203+0304=31,得,
所以,解得a=16,即AB=B0=16,所以BC=32,
所以长方形花坛ABCD的周长是2(16+32)=96m.
二、填空题(共6小题,每小题4分,满分24分)
11、在四边形ABCD中,∠A=∠B=∠C=∠D,则四边形ABCD是 矩形 .
【解答】 解:∵∠A+∠B+∠C+∠D=360°,且∠A=∠B=∠C=∠D,
∴∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是矩形.
故答案为:矩形
12、如图,菱形ABCD中,对角线AC交BD于O,AB=8,E是CB的中点,则OE的长等于 .21世纪教育网版权所有
【解答】 解:∵四边形ABCD是菱形,
∴DO=OB,
∵E是AD的中点,
∴OE=AB,
∵AB=8,
∴OE=4.
故答案为4.
13、矩形的两邻边长的差为2,对角线长为4,则矩形的面积为 .
【解答】 解: 设矩形一条边长为x,则另一条边长为x﹣2,
由勾股定理得,x2+(x﹣2)2=42,
整理得,x2﹣2x﹣6=0,
解得:x=1+或x=1﹣(不合题意,舍去),
另一边为:﹣1,
则矩形的面积为:(1+)(﹣1)=6.
故答案为:6.
14、如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是 8 .www.21-cn-jy.com
【解答】 解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=AC=2,OD=BD,AC=BD,
∴OC=OD=2,
∴四边形CODE是菱形,
∴DE=CEOC=OD=2,
∴四边形CODE的周长=2×4=8;
故答案为:8.
15、如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 6 .
【解答】 解:∵四边形ABCD是矩形,
∴AB=DC=8,∠D=90°,
∵将矩形ABCD沿CE折叠后,点B落在AD边的F点上,
∴CF=BC=10,
在Rt△CDF中,由勾股定理得:DF===6,
故答案为:6.
16、菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2015秒时,点P的坐标为 (0.5,﹣) .21·cn·jy·com
【解答】 解:∵A(1,0),B(0,),
∴AB==2.
∵点P的运动速度为0.5米/秒,
∴从点A到点B所需时间==4秒,
∴沿A→B→C→D→A所需的时间=4×4=16秒.
∵=125…15,
∴移动到第2015秒时,点P恰好运动到AD的中点,
∴P(0.5,﹣).
故答案为:(0.5,﹣).
三、解答题(本题有7个小题,共66分)解答应写出证明过程或推演步骤.
17、(6分)如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,选择的条件是 ③ (只填写序号).【来源:21·世纪·教育·网】
【解答】 解:∵BD=CD,DE=DF,
∴四边形BECF是平行四边形,
①BE⊥EC时,四边形BECF是矩形,不一定是菱形;
②四边形BECF是平行四边形,则BF∥EC一定成立,故不一定是菱形;
③AB=AC时,∵D是BC的中点,
∴AF是BC的中垂线,
∴BE=CE,
∴平行四边形BECF是菱形.
故答案是:③.
18、(8分)为美化环境,某单位需要在一块正方形空地上分别种植四种不同的花草,计划将这块空地按如下要求分成四块:⑴分割后的整个图形必须是中心对称图形;⑵四块图形的形状相同;⑶四块图形的面积相等.
请按照上述三个要求,分别在下面的正方形中给出4种不同的分割方法.
(尺规或徒手作图均可,但要尽可能准确、美观些,不写画法)
【解答】 解:分割方案如下:
点评:本题是方法开放型问题,按要求的分法很多,要想将正方形分成面积相等的四部分,只要过正方形的中心画两条垂直的直线即可,另外探索性学习方式是新课程的要求,也是新课标的要求,能改变学生的学习方式
19、(8分)在平面直角坐标系xoy中 ,直线y=-x+3 与x轴、y轴分别教育A、B ,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标。2-1-c-n-j-y
【解答】 解:分两种情况;
①如图1,令x=0,则y=3,令y=0,则x=3,
∴OA=OB=3,
∴∠BAO=45°,
∵DE⊥OA,
∴DE=AE,
∵四边形COED是正方形,
∴OE=DE,
∴OE=AE,
∴OE=OA=,
∴E(,0);
②如图2,由①知△OFC,△EFA是等腰直角三角形,
∴CF=OF,AF=EF,
∵四边形CDEF是正方形,
∴EF=CF,
∴AF=OF=2OF,
∴OA=OF+2OF=3,
∴OF=1,
∴F(1,0).
20、(10分)如图1,纸片□ABCD中,AD=5,S□ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( ) 21*cnjy*com
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
【解答】 解:(1) 由平移知:AEDE′,
∴四边形AEE′D是平行四边形,又AE⊥BC, ∴∠AEE′=90°,
∴四边形AEE′D是矩形,∴C选项正确.
① ∵AFDF′, ∴四边形AFF′D是平行四边形,
∵AE=3, EF=4 ,∠E=90°, ∴AF=5,
∵S□ABCD=AD·AE=15, ∴AD=5 , ∴AD=AF , ∴四边形AFF′D是菱形.
② 如下图, 连接AF′, DF ,
在Rt△AEF′中, AE=3, EF′=9, ∴AF′=
在Rt△DFE′中, FE′=1, DE′=AE=3, ∴DF=
∴四边形AFF′D两条对角线的长分别是和 .
21、(10分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=6,BC=8,求MD的长.
【解答】 解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
在△DMO和△BNO中,
,
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+62,
解得:x=.
答:MD长为.
22、(12分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【解答】 解:(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
, ∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠E,
∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE;
23、(12分)如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
解答: 解:(1)如图2,DM=FM,DM⊥FM,
证明:连接DF,NF,
∵四边形ABCD和CGEF是正方形,
∴AD∥BC,BC∥GE,
∴AD∥GE,
∴∠DAM=∠NEM,
∵M是AE的中点,
∴AM=EM,
在△MAD与△MEN中,
,∴△MAD≌△MEN,
∴DM=MN,AD=EN,
∵AD=CD,
∴CD=NE,
∵CF=EF,∠DCF=∠DCB=90°,
在△DCF与△NEF中,
,∴△MAD≌△MEN,
∴DF=NF,∠CFD=∠EFN,
∵∠EFN+∠NFC=90°,
∴∠DFC+∠CFN=90°,
∴∠DFN=90°,
∴DM⊥FM,DM=FM
(2)猜想:DM⊥FM,DM=FM,
证明如下:如图3,连接DF,NF,
连接DF,NF,
∵四边形ABCD是正方形,
∴AD∥BC,
∵点E、B、C在同一条直线上,
∴AD∥CN,
∴∠ADN=∠MNE,
在△MAD与△MEN中,
,∴△MAD≌△MEN,
∴DM=MN,AD=EN,
∵AD=CD,
∴CD=NE,
∵CF=EF,
∵∠DCF=90°+45°=135°,∠NEF=180°﹣45°=135°,
∴∠DCF=∠NEF,
在△DCF与△NEF中,
,∴△MAD≌△MEN,
∴DF=NF,∠CFD=∠EFN,
∵∠CFD+∠EFD=90°,
∴∠NFE+∠EFD=90°,
∴∠DFN=90°,
∴DM⊥FM,DM=FM.
班级 姓名 学号
一、选择题(共10小题,每小题3分,满分30分)
1、如图,在菱形中,,∠,则对角线等于( )
A.20 B.15 C.10 D.5
2、下列命题是真命题的是( )
A. 一组对边平行,另一组对边相等的四边形是平行四边形
B. 对角线互相垂直的平行四边形是矩形
C. 四条边相等的四边形是菱形
D. 正方形是轴对称图形,但不是中心对称图形
3、已知四边形ABCD是平行四边形,若要使它成为正方形,则应增加的条件是
( )
A. AC⊥BD B.AC=BD C.AC=BD且AC⊥BD D. AC平分∠BAD
4、如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=,BD=4,则菱形ABCD的周长为( )
A. 4 B. 4 C. 4 D.28
5、已知,在等腰△ABC中,AB=AC,分别延长BA,CA到D,E点,使DA=AB,EA=CA,则四边形BCDE是( )2·1·c·n·j·y
A. 任意四边形 B.矩形 C.菱形 D. 正方形
6、如图,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)
的面积是( )
A. 2 B. C.1 D.
7、如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿
AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )
A.1或2 B.2或3 C.3或4 D. 4或5
8、在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,自D作DH⊥AB于H,则DH的长是( )www-2-1-cnjy-com
A. 7.5 B.7 C.6.5 D. 5.5
9、△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )【来源:21cnj*y.co*m】
A. 2cm,2cm,2cm B.3cm,3cm,3cm
C.4cm,4cm,4cm D.2cm, 3cm,5cm
10、如图1,是由两个正方形组成的长方形花坛ABCD,
小明从顶点A沿着花坛间小路直到走到长边中点O,
再从中点O走到正方形OCDF的中心O1,再从中心
O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走到正方形O3KJP
的中心O4,一共走了31m,则长方形花坛ABCD的周长是( )m.
A.36 B. 48 C. 96 D. 60
二、填空题(共6小题,每小题4分,满分24分)
11、在四边形ABCD中,∠A=∠B=∠C=∠D,则四边形ABCD是 .
12、如图,菱形ABCD中,对角线AC交BD于O,AB=8,E是CB的中点,则OE的长等于 .
13、矩形的两邻边长的差为2,对角线长为4,则矩形的面积为 .
14、如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是 .
15、如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 .
16、菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2015秒时,点P的坐标为 .21cnjy.com
三、解答题(本题有7个小题,共66分)解答应写出证明过程或推演步骤.
17、(6分)如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,选择的条件是 (只填写序号).
18、(8分)为美化环境,某单位需要在一块正方形空地上分别种植四种不同的花草,计划将这块空地按如下要求分成四块:⑴分割后的整个图形必须是中心对称图形;⑵四块图形的形状相同;⑶四块图形的面积相等.
请按照上述三个要求,分别在下面的正方形中给出4种不同的分割方法.
(尺规或徒手作图均可,但要尽可能准确、美观些,不写画法)
19、(8分)在平面直角坐标系xoy中 ,直线y=-x+3 与x轴、y轴分别教育A、B ,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标。
20、(10分)如图1,纸片□ABCD中,AD=5,S□ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
21、(10分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=6,BC=8,求MD的长.
22、(12分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.21教育网
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
23、(12分)如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)【出处:21教育名师】
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
答案详解
一、选择题(共10小题,每小题3分,满分30分)
【解答】 解:
A、一组对边平行,且相等的四边形是平行四边形,所以A选项错误;
B、对角线互相垂直,且相等的平行四边形是矩形,所以B选项错误;
C、四条边相等的四边形是菱形,所以C选项正确;
D、正方形是轴对称图形,也是中心对称图形,所以D选项错误.
故选C.
3、已知四边形ABCD是平行四边形,若要使它成为正方形,则应增加的条件是( )
A. AC⊥BD B.AC=BD C.AC=BD且AC⊥BD D. AC平分∠BAD
【解答】 解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,故错误;
B、∵四边形ABCD是平行四边形,AC=BD,
∴四边形ABCD是矩形,故错误;
C、∵四边形ABCD是平行四边形,AC⊥BD,
∴四边形ABCD是菱形,
∵AC=BD, ∴四边形ABCD是正方形,故正确;
D、∵四边形ABCD是平行四边形,AC平分∠BAD,
∴四边形ABCD是矩形,故错误.
故选C.
4、如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF=,BD=4,则菱形ABCD的周长为( )
A. 4 B. 4 C. 4 D.28
【解答】 解:∵E,F分别是AB,BC边上的中点,EF=,
∴AC=2EF=2,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=,OB=BD=2,
∴AB==,
∴菱形ABCD的周长为4.
故选:C.
5、已知,在等腰△ABC中,AB=AC,分别延长BA,CA到D,E点,使DA=AB,EA=CA,则四边形BCDE是( )21教育名师原创作品
A. 任意四边形 B.矩形 C.菱形 D. 正方形
【解答】 解:如图所示,
∵AC=AE,AB=AD
∴四边形BCDE为平行四边形,
∵AB=AE,∴∠AEB=∠ABE,
∵∠BAC+∠ABC+∠ACB=180°
∠ABC=∠ACB
∴∠ABC+∠EBA=90°
∴四边形BCDE为矩形.
故选B.
6、如图,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( )
A. 2 B. C.1 D.
【解答】 解:因为在直角三角形中30度角对应的直角边是斜边的一半,
在题目中的菱形中,已知菱形的高为1,可得边长为2,
所以面积为2.
故选:A.
7、如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为( )21*cnjy*com
A.1或2 B.2或3 C.3或4 D. 4或5
【解答】 解:如图,连接B′D,过点B′作B′M⊥AD于M.
∵点B的对应点B′落在∠ADC的角平分线上,
∴设DM=B′M=x,则AM=7﹣x,
又由折叠的性质知AB=AB′=5,
∴在直角△AMB′中,由勾股定理得到:AM2=AB′2﹣B′M2
即(7﹣x)2=25﹣x2,
解得x=3或x=4,
则点B′到BC的距离为2或1.
故选:A.
8、在四边形ABCD中,∠A=60°,∠ABC=∠ADC=90°,BC=2,CD=11,自D作DH⊥AB于H,则DH的长是( )【版权所有:21教育】
A. 7.5 B.7 C.6.5 D. 5.5
【解答】 解:过C作DH的垂线CE交DH于E,
∵DH⊥AB,CB⊥AB,
∴CB∥DH又CE⊥DH,
∴四边形BCEH是矩形.
∵HE=BC=2,在Rt△AHD中,∠A=60°,
∴∠ADH=30°,
又∵∠ADC=90°
∴∠CDE=60°,
∴∠DCE=30°,
∴在Rt△CED中,DE=CD=5.5,
∴DH=2+5.5=7.5.
故选A.
9、△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A. 2cm,2cm,2cm B.3cm,3cm,3cm
C.4cm,4cm,4cm D.2cm, 3cm,5cm
【解答】 解:解答:解:连接OA,OB,OC,则△BDO≌△BFO,△CDO≌△CEO,△AEO≌△AFO,21·世纪*教育网
∴BD=BF,CD=CE,AE=AF,
又∵∠C=90,OD⊥BC于D,OE⊥AC于E,且O为△ABC三条角平分线的交点
∴四边形OECD是正方形,
则点O到三边AB、AC、BC的距离=CD,
∴AB=8﹣CD+6﹣CD=﹣2CD+14,又根据勾股定理可得:AB=10,
即﹣2CD+14=10
∴CD=2,
即点O到三边AB、AC、BC的距离为2cm.
故选A
10、如图1,是由两个正方形组成的长方形花坛ABCD,
小明从顶点A沿着花坛间小路直到走到长边中点O,
再从中点O走到正方形OCDF的中心O1,再从中心
O1走到正方形O1GFH的中心O2,又从中心O2走到正方形O2IHJ的中心O3,再从中心O3走到正方形O3KJP
的中心O4,一共走了31m,则长方形花坛ABCD的周长是( )m.
A.36 B. 48 C. 96 D. 60
【解答】 解:设AB=BO=a,根据勾股定理,得AO=a,
所以001=,O1O2=,0203=,0304=.
由A0+001+0102+0203+0304=31,得,
所以,解得a=16,即AB=B0=16,所以BC=32,
所以长方形花坛ABCD的周长是2(16+32)=96m.
二、填空题(共6小题,每小题4分,满分24分)
11、在四边形ABCD中,∠A=∠B=∠C=∠D,则四边形ABCD是 矩形 .
【解答】 解:∵∠A+∠B+∠C+∠D=360°,且∠A=∠B=∠C=∠D,
∴∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是矩形.
故答案为:矩形
12、如图,菱形ABCD中,对角线AC交BD于O,AB=8,E是CB的中点,则OE的长等于 .21世纪教育网版权所有
【解答】 解:∵四边形ABCD是菱形,
∴DO=OB,
∵E是AD的中点,
∴OE=AB,
∵AB=8,
∴OE=4.
故答案为4.
13、矩形的两邻边长的差为2,对角线长为4,则矩形的面积为 .
【解答】 解: 设矩形一条边长为x,则另一条边长为x﹣2,
由勾股定理得,x2+(x﹣2)2=42,
整理得,x2﹣2x﹣6=0,
解得:x=1+或x=1﹣(不合题意,舍去),
另一边为:﹣1,
则矩形的面积为:(1+)(﹣1)=6.
故答案为:6.
14、如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是 8 .www.21-cn-jy.com
【解答】 解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=AC=2,OD=BD,AC=BD,
∴OC=OD=2,
∴四边形CODE是菱形,
∴DE=CEOC=OD=2,
∴四边形CODE的周长=2×4=8;
故答案为:8.
15、如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 6 .
【解答】 解:∵四边形ABCD是矩形,
∴AB=DC=8,∠D=90°,
∵将矩形ABCD沿CE折叠后,点B落在AD边的F点上,
∴CF=BC=10,
在Rt△CDF中,由勾股定理得:DF===6,
故答案为:6.
16、菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2015秒时,点P的坐标为 (0.5,﹣) .21·cn·jy·com
【解答】 解:∵A(1,0),B(0,),
∴AB==2.
∵点P的运动速度为0.5米/秒,
∴从点A到点B所需时间==4秒,
∴沿A→B→C→D→A所需的时间=4×4=16秒.
∵=125…15,
∴移动到第2015秒时,点P恰好运动到AD的中点,
∴P(0.5,﹣).
故答案为:(0.5,﹣).
三、解答题(本题有7个小题,共66分)解答应写出证明过程或推演步骤.
17、(6分)如图,在△ABC中,点D是BC的中点,点E、F分别是线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC,从中选择一个条件使四边形BECF是菱形,并给出证明,选择的条件是 ③ (只填写序号).【来源:21·世纪·教育·网】
【解答】 解:∵BD=CD,DE=DF,
∴四边形BECF是平行四边形,
①BE⊥EC时,四边形BECF是矩形,不一定是菱形;
②四边形BECF是平行四边形,则BF∥EC一定成立,故不一定是菱形;
③AB=AC时,∵D是BC的中点,
∴AF是BC的中垂线,
∴BE=CE,
∴平行四边形BECF是菱形.
故答案是:③.
18、(8分)为美化环境,某单位需要在一块正方形空地上分别种植四种不同的花草,计划将这块空地按如下要求分成四块:⑴分割后的整个图形必须是中心对称图形;⑵四块图形的形状相同;⑶四块图形的面积相等.
请按照上述三个要求,分别在下面的正方形中给出4种不同的分割方法.
(尺规或徒手作图均可,但要尽可能准确、美观些,不写画法)
【解答】 解:分割方案如下:
点评:本题是方法开放型问题,按要求的分法很多,要想将正方形分成面积相等的四部分,只要过正方形的中心画两条垂直的直线即可,另外探索性学习方式是新课程的要求,也是新课标的要求,能改变学生的学习方式
19、(8分)在平面直角坐标系xoy中 ,直线y=-x+3 与x轴、y轴分别教育A、B ,在△AOB内部作正方形,使正方形的四个顶点都落在该三角形的边上,求正方形落在x轴正半轴的顶点坐标。2-1-c-n-j-y
【解答】 解:分两种情况;
①如图1,令x=0,则y=3,令y=0,则x=3,
∴OA=OB=3,
∴∠BAO=45°,
∵DE⊥OA,
∴DE=AE,
∵四边形COED是正方形,
∴OE=DE,
∴OE=AE,
∴OE=OA=,
∴E(,0);
②如图2,由①知△OFC,△EFA是等腰直角三角形,
∴CF=OF,AF=EF,
∵四边形CDEF是正方形,
∴EF=CF,
∴AF=OF=2OF,
∴OA=OF+2OF=3,
∴OF=1,
∴F(1,0).
20、(10分)如图1,纸片□ABCD中,AD=5,S□ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( ) 21*cnjy*com
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
【解答】 解:(1) 由平移知:AEDE′,
∴四边形AEE′D是平行四边形,又AE⊥BC, ∴∠AEE′=90°,
∴四边形AEE′D是矩形,∴C选项正确.
① ∵AFDF′, ∴四边形AFF′D是平行四边形,
∵AE=3, EF=4 ,∠E=90°, ∴AF=5,
∵S□ABCD=AD·AE=15, ∴AD=5 , ∴AD=AF , ∴四边形AFF′D是菱形.
② 如下图, 连接AF′, DF ,
在Rt△AEF′中, AE=3, EF′=9, ∴AF′=
在Rt△DFE′中, FE′=1, DE′=AE=3, ∴DF=
∴四边形AFF′D两条对角线的长分别是和 .
21、(10分)如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接MN,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=6,BC=8,求MD的长.
【解答】 解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
在△DMO和△BNO中,
,
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+62,
解得:x=.
答:MD长为.
22、(12分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【解答】 解:(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
, ∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠E,
∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE;
23、(12分)如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
解答: 解:(1)如图2,DM=FM,DM⊥FM,
证明:连接DF,NF,
∵四边形ABCD和CGEF是正方形,
∴AD∥BC,BC∥GE,
∴AD∥GE,
∴∠DAM=∠NEM,
∵M是AE的中点,
∴AM=EM,
在△MAD与△MEN中,
,∴△MAD≌△MEN,
∴DM=MN,AD=EN,
∵AD=CD,
∴CD=NE,
∵CF=EF,∠DCF=∠DCB=90°,
在△DCF与△NEF中,
,∴△MAD≌△MEN,
∴DF=NF,∠CFD=∠EFN,
∵∠EFN+∠NFC=90°,
∴∠DFC+∠CFN=90°,
∴∠DFN=90°,
∴DM⊥FM,DM=FM
(2)猜想:DM⊥FM,DM=FM,
证明如下:如图3,连接DF,NF,
连接DF,NF,
∵四边形ABCD是正方形,
∴AD∥BC,
∵点E、B、C在同一条直线上,
∴AD∥CN,
∴∠ADN=∠MNE,
在△MAD与△MEN中,
,∴△MAD≌△MEN,
∴DM=MN,AD=EN,
∵AD=CD,
∴CD=NE,
∵CF=EF,
∵∠DCF=90°+45°=135°,∠NEF=180°﹣45°=135°,
∴∠DCF=∠NEF,
在△DCF与△NEF中,
,∴△MAD≌△MEN,
∴DF=NF,∠CFD=∠EFN,
∵∠CFD+∠EFD=90°,
∴∠NFE+∠EFD=90°,
∴∠DFN=90°,
∴DM⊥FM,DM=FM.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
