3.1平均数同步练习(含解析) 2024—2025学年浙教版八年级下册
文档属性
| 名称 | 3.1平均数同步练习(含解析) 2024—2025学年浙教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 458.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 00:00:00 | ||
图片预览




文档简介
3.1平均数同步练习—2024—2025学年浙教版八年级下册
一、单选题
1.某校组织“庆国庆”画展,参展的彩铅、水墨、水彩、速写四个类别作品幅数分别为:58,56,58,60,则这组数据的平均数为( )
A.56 B.57 C.58 D.59
2.体育学科越来越得到重视,某中学规定学生的学期体育成绩满分分,其中健康知识考试成绩占,体育技能考试成绩占,小明的这三项成绩(百分制)依次为,则小明这学期的体育成绩为( )
A. B. C. D.
3.某校评选先进班集体,从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分,各项满分均为100,所占比例如下表:
项目 学习 卫生 纪律 活动参与
所占比例
八(1)班这四项得分依次为80,90,86,70,则该班四项综合得分(满分100)为( )
A. B.83 C.84 D.86
4.某工厂生产质量分别为1g,5g,10g,25g四种规格的球,现从中取x个球装到一个空箱子里,这时箱子里球的平均质量为20g,若再放入一个25g的球,此时箱子里球的平均质量变为21g,则x的值为( )
A.3 B.4 C.5 D.6
5.若一组数据,,,,的平均数为,那么数据,,,,的平均数为( )
A. B. C. D.
6.某次测试结束,嘉琪随机抽取了九(1)班学生的成绩进行统计,并绘制成如图所示的扇形统计图,则该班学生的平均成绩为( )
A.9分 B.分 C.分 D.8分
7.若一组数据2,4,5,1,a的平均数为a,则a=( )
A.1 B.2.4 C.2 D.3
8.某学校考查各个班级的教室卫生状况时包括以下三项:地面、黑板,门窗,其中“地面”最重要,“黑板”次之,“门窗”要求最低,根据这个要求,对地面、黑板、门窗三项考察比较合适的比例设计分别为( )
A.,, B.,,
C.,, D.,,
二、填空题
9.若个数,,…的平均数是,则,,…,的平均数是 .
10.某校欲招聘一名初中数学教师.对甲、乙、丙三名应聘者进行了专业知识、教育理论、模拟课堂等三方面的测试,他们的各项成绩(单位:分)如下表所示:
专业知识 教育理论 模拟课堂
甲 67 73 86
乙 75 65 86
丙 72 71 75
如果将每位应聘者的专业知识、教育理论、模拟课堂的成绩按的比例确定,并录用平均成绩(百分制)最高的应聘者,则被录用的是 .
11.已知,,,…,的平均数,求,,…,的平均数为 .
12.体育锻炼是增强体质有效的手段,小王一学期的体育平时成绩为90分,期中成绩为94分,期末成绩为95分,若学校规定平时成绩、期中成绩、期末成绩三项得分按的比例确定最终成绩,则小王的最终成绩为 分.
13.某校把学生的纸笔测试、实践能力两项成绩分别按、的比例计入学期总成绩,小明实践能力得分,若想学期总成绩不低于分,则纸笔测试的成绩至少是 .
三、解答题
14.某校在一次演讲比赛中,甲,乙的各项得分如表.
演讲内容 语言表达 临场表现
甲 90 85 80
乙 84 83 91
(1)如果根据三项得分的平均分从高到低确定名次,那么两位同学的排名顺序怎样?
(2)若学校认为这三个项目的重要程度有所不同,而给予“演讲内容”“语言表达”“临场表现”三个项目在总分中的占比为,那么两位同学的排名顺序又怎样?
15.某校随机抽取若干名八年级学生进行体能测试,成绩记为分,分,分,分四个等级,将调查结果绘制成如下条形统计图(图1)和扇形统计图(图2).根据图中信息,回答下列问题:
(1)这次一共抽查了几名学生.
(2)求所抽查的学生的平均分数.
(3)该校有名学生,估计该校有多少名学生体能测试成绩不小于分.
16.某班进行“闪亮之星”的推选工作,经过自荐和第一轮筛选后,甲、乙两位同学进入终选.如表为甲、乙两位同学的得分情况.其中人气分的计算方法是:根据班级主科老师和同学的投票结果,老师一票记10分,同学一票记2分,两个分数相加即为人气分.
学生 人气分 学习分 行规分 工作分
老师票数 同学票数 分数
甲 4 20 a 85 95 85
乙 b 25 70 90 92 90
(1)__________,__________;
(2)经全班同学讨论决定,将人气、学习、行规、工作四个方面在总分中所占的比例分别为.经计算,甲同学的最终得分为87分,请你求出乙同学的最终得分,并判断哪位同学当选.
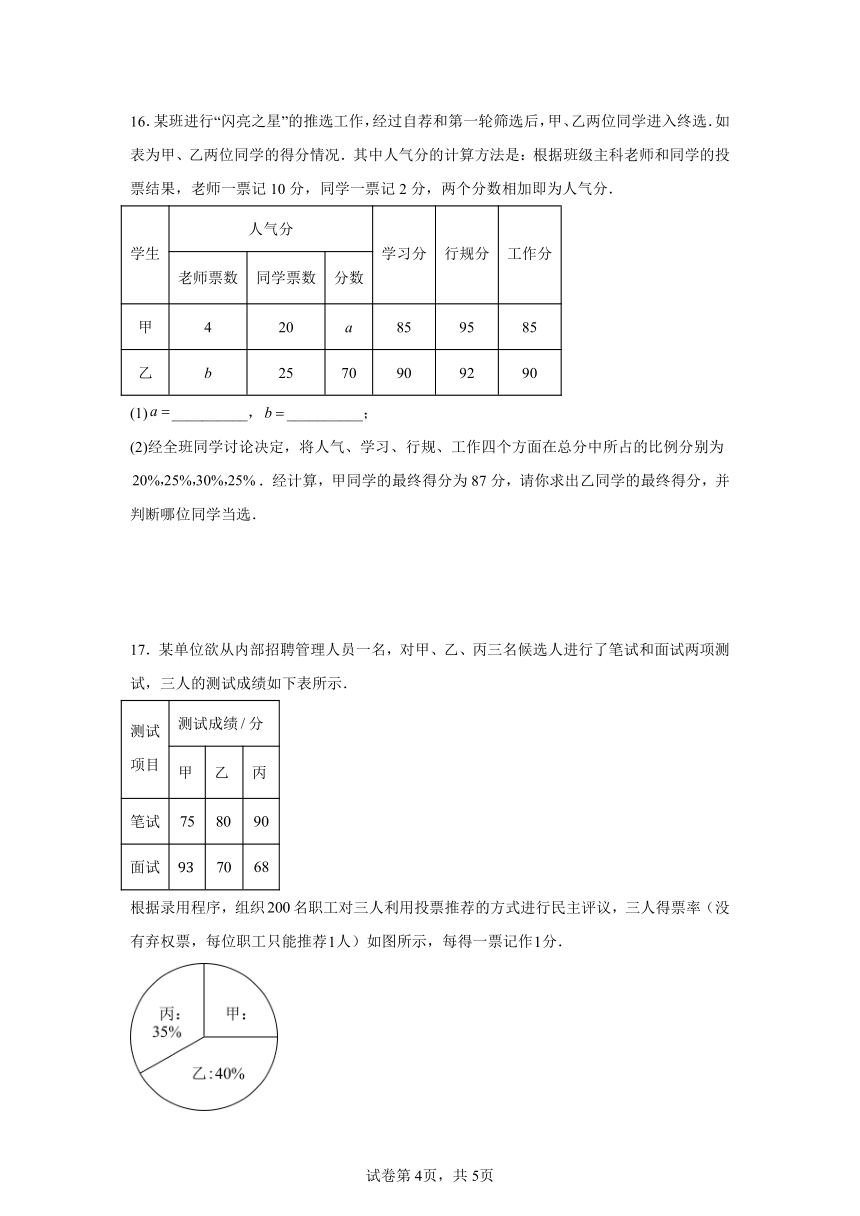
17.某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.
测试 项目 测试成绩分
甲 乙 丙
笔试
面试
根据录用程序,组织名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐人)如图所示,每得一票记作分.
(1)甲的民主评议得分为 分;如果根据三项测试的平均成绩确定录用人选,那么 将被录用.
(2)根据实际需要,单位将笔试、面试、民主评议三项测试得分按的比例确定个人成绩,那么谁将被录用?(请写出计算过程)
18.某班准备选取一名同学参加校级知识竞赛,需对甲、乙、丙三名候选人进行笔试和口试,并组织全班40名同学民主投票(无弃权且每人只能投1票,每得一票记作2分).测试成绩与得票率分别统计如下:
测试项目 测试成绩(分)
甲 乙 丙
笔试 75 80 84
口试 90 80 80
(1)请算出三人的得票分.
(2)通过计算说明根据笔试、口试、投票三项得分的平均数是否可确定人选.
(3)如果将笔试,口试,投票三项得分按,,计入个人成绩,请说明谁将被选中.
试卷第1页,共3页
试卷第1页,共3页
《3.1平均数同步练习—2024—2025学年浙教版八年级下册》参考答案
题号 1 2 3 4 5 6 7 8
答案 C B B B B A D B
1.C
【分析】本题考查了求一组数的平均数,根据求平均数的公式列式计算,即可作答.
【详解】解:∵参展的彩铅、水墨、水彩、速写四个类别作品幅数分别为:58,56,58,60,
∴,
∴这组数据的平均数为58,
故选:C.
2.B
【分析】本题考查了加权平均数,根据加权平均数的计算方法计算即可,解题的关键是明确加权平均数的计算方法.
【详解】解:由题意可得,
小明这学期的体育成绩为分,
故选:.
3.B
【分析】本题考查加权平均数,根据题意和加权平均数的计算方法,可以计算出八(1)班四项综合得分(满分100),本题得以解决.
【详解】解:(分),
即八(1)班四项综合得分(满分100)为分,
故选:B.
4.B
【分析】本题主要考查了分式方程的应用,平均数,先根据平均值等于21列出方程,再求出解,检验可得答案.
【详解】根据题意,得
,
解得.
经检验,是原方程的根.
所以,x的值是4.
故选:B.
5.B
【分析】根据数据,,,,的平均数为可知,据此可得出的值.
【详解】解:数据,,,,的平均数为,
,
,
数据,,,,的平均数为.
故选:B.
【点睛】此题主要考查了平均数,熟记平均数是解答此题的关键.
6.A
【分析】本题考查的是加权平均数的含义,直接利用加权平均数的含义计算即可.
【详解】解:平均成绩为:
(分).
故选 A.
7.D
【分析】根据平均数的定义列出方程求解可得;
【详解】∵一组数据 的平均数为
解得:
故选D
【点睛】本题主要考查算术平均数,解题的关键是熟练掌握平均数的定义;平均数是指在一组数据中所有数据之和再除以数据的个数;它是反映数据集中趋势的一项指标
8.B
【分析】根据题意可知:“地面”最重要,“黑板”次之,“门窗”要求最低,再观察各个选项,可得答案.
【详解】解:“地面”最重要,“黑板”次之,“门窗”要求最低,
对地面、黑板、门窗三项考察比较合适的比例设计分别为,,,
故选:B.
【点睛】本题主要考查了加权平均数,解答本题的关键是明确权的意义.
9.4
【分析】本题主要考查了平均数,根据平均数的定义即可求解,熟练掌握平均数是指在一组数据中所有数据之和再除以数据的个数是解决此题的关键.
【详解】解:∵个数,,…的平均数是,
,
,
,,…….,平均数
,
故答案为:4.
10.乙
【分析】本题考查加权平均数,解答本题的关键是明确题意,求出相应的加权平均数.根据表格中的数据和加权平均数的计算方法,可以分别求出甲、乙、丙的成绩,然后比较大小即可.
【详解】解:由题意可得,
甲的成绩为:
乙的成绩为:
丙的成绩为:
∵,
∴乙将被录取,
故答案为:乙.
11.
【分析】本题考查了平均数.由题意知,,,,,的和为,则可计算出,,,的和,除以10,即为新数据的平均数.
【详解】解:,,,,的平均数为
,,,的平均数.
故答案为:.
12.
【分析】本题考查了加权平均数的求法,根据加权平均数的计算方法列式进行计算是解题的关键.
【详解】解:小王的最终成绩为分,
故答案为:.
13.分
【分析】本题考查了加权平均数、一元一次不等式的应用,设小明的纸笔测试的成绩是分,根据加权平均数列出不等式,求解即可,熟练掌握加权平均数、正确列出一元一次不等式是解题的关键.
【详解】解:设小明的纸笔测试的成绩是分,
由题意得:
解得:,
∴纸笔测试的成绩至少是分,
故答案为:分.
14.(1)根据三项得分的平均数从高到低确定名次,乙第一,甲第二
(2)两个的排名顺序发生变化,甲第一,乙第二
【分析】本题考查算术平均数、加权平均数的意义及计算方法,体会“权”在求平均数时的作用.
(1)根据算术平均数的计算方法计算甲、乙的平均数,通过比较得出得出结论.
(2)利用加权平均数的计算方法分别计算甲、乙的总评成绩,比较做出判断即可.
【详解】(1)解:甲的算术平均数:,
乙的算术平均数:.
因此第一名是乙,第二名是甲,
答:根据三项得分的平均数从高到低确定名次,乙第一,甲第二.
(2)解:甲班的总评成绩:,
乙班的总评成绩:,
,
∴甲高于乙,
答:两个的排名顺序发生变化,甲第一,乙第二.
15.(1)名
(2)分
(3)名
【分析】本题考查了条形统计图,扇形统计图,求平均数,用样本估计总体;读懂统计图,从不同的统计图中得到必要的信息是解答本题的关键.
(1)根据“分”的人数除以其占调查人数的比例,即可求出调查人数;
(2)先求出“分”和“分”的人数,再根据平均数是指在一组数据中所有数据之和再除以数据的个数,计算即可;
(3)用总人数乘以“分”和“分”占调查人数的比例,即可求解.
【详解】(1)解:依题意得,“分”的人数有人,占调查人数的,
∴共抽取学生(人);
故这次一共抽查了名学生.
(2)解:“分”的人数占调查人数的,
∴“分”的人数为:(人),
“分”的人数为:(人),
抽取的所有学生成绩的平均数是:(分).
故抽取的所有学生成绩的平均数为分.
(3)解:(人),
故估计该校有名学生体能测试成绩不小于分.
16.(1)80;2;
(2)乙的得分为分,甲同学当选
【分析】本题主要考查了有理数的四则运算,求加权平均数:
(1)根据表格中的数据以及老师一票记10分,同学一票记2分进行列式求解即可;
(2)根据加权平均数的求解方法求解即可.
【详解】(1)解:由题意得,,,
故答案为:80;2;
(2)解:乙的最终得分为分,
∵,
∴甲同学当选.
17.(1),乙
(2)丙将被录用
【分析】(1)根据扇形统计图得出每部分所占的百分比,求出甲、乙、丙民主评议的得分,再根据平均数的计算公式求出各自的平均数,然后进行比较,即可得出答案;
(2)利用加权平均数的计算公式列式计算求出三人的得分,然后即可判断录用的候选人.
【详解】(1)解:甲的民主评议得分为:(分,
乙的民主评议得分为:(分,
丙的民主评议得分为:(分,
甲的平均成绩是:(分,
乙的平均成绩是:(分,
丙的平均成绩是:(分,
根据三项测试的平均成绩确定录用人选,那么乙被录用;
故答案为:50,乙;
(2)解:将笔试、面试、民主评议三项测试得分按的比例,
则甲得分:(分,
乙得分:(分,
丙得分:(分,
则丙将被录用.
【点睛】本题考查的是加权平均数的求法,要注意各部分的权重与相应的数据的关系,根据公式列出算式是解题的关键.
18.(1)甲20分,乙32分,丙28分
(2)无法确定人选
(3)丙被选中
【分析】(1)根据得票数,求出三人的得票分即可;
(2)分别算出甲、乙、丙三人的平均分,进行判断即可;
(3)分别算出三个人的加权平均数,然后进行判断即可.
【详解】(1)解:甲的得票分为:(分),
乙的得票分为:(分),
丙的得票分为:(分).
(2)解:甲的平均分为:(分),
乙的平均分为:(分),
丙的平均分为:(分),
∵乙和丙的平均分相同,
∴无法确定人选.
(3)解:甲:(分).
乙:(分).
丙:(分).
∴丙被选中.
【点睛】本题主要考查了加权平均数的计算,利用平均数和加权平均数做决策,解题的关键是准确求出平均数和加权平均数.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某校组织“庆国庆”画展,参展的彩铅、水墨、水彩、速写四个类别作品幅数分别为:58,56,58,60,则这组数据的平均数为( )
A.56 B.57 C.58 D.59
2.体育学科越来越得到重视,某中学规定学生的学期体育成绩满分分,其中健康知识考试成绩占,体育技能考试成绩占,小明的这三项成绩(百分制)依次为,则小明这学期的体育成绩为( )
A. B. C. D.
3.某校评选先进班集体,从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分,各项满分均为100,所占比例如下表:
项目 学习 卫生 纪律 活动参与
所占比例
八(1)班这四项得分依次为80,90,86,70,则该班四项综合得分(满分100)为( )
A. B.83 C.84 D.86
4.某工厂生产质量分别为1g,5g,10g,25g四种规格的球,现从中取x个球装到一个空箱子里,这时箱子里球的平均质量为20g,若再放入一个25g的球,此时箱子里球的平均质量变为21g,则x的值为( )
A.3 B.4 C.5 D.6
5.若一组数据,,,,的平均数为,那么数据,,,,的平均数为( )
A. B. C. D.
6.某次测试结束,嘉琪随机抽取了九(1)班学生的成绩进行统计,并绘制成如图所示的扇形统计图,则该班学生的平均成绩为( )
A.9分 B.分 C.分 D.8分
7.若一组数据2,4,5,1,a的平均数为a,则a=( )
A.1 B.2.4 C.2 D.3
8.某学校考查各个班级的教室卫生状况时包括以下三项:地面、黑板,门窗,其中“地面”最重要,“黑板”次之,“门窗”要求最低,根据这个要求,对地面、黑板、门窗三项考察比较合适的比例设计分别为( )
A.,, B.,,
C.,, D.,,
二、填空题
9.若个数,,…的平均数是,则,,…,的平均数是 .
10.某校欲招聘一名初中数学教师.对甲、乙、丙三名应聘者进行了专业知识、教育理论、模拟课堂等三方面的测试,他们的各项成绩(单位:分)如下表所示:
专业知识 教育理论 模拟课堂
甲 67 73 86
乙 75 65 86
丙 72 71 75
如果将每位应聘者的专业知识、教育理论、模拟课堂的成绩按的比例确定,并录用平均成绩(百分制)最高的应聘者,则被录用的是 .
11.已知,,,…,的平均数,求,,…,的平均数为 .
12.体育锻炼是增强体质有效的手段,小王一学期的体育平时成绩为90分,期中成绩为94分,期末成绩为95分,若学校规定平时成绩、期中成绩、期末成绩三项得分按的比例确定最终成绩,则小王的最终成绩为 分.
13.某校把学生的纸笔测试、实践能力两项成绩分别按、的比例计入学期总成绩,小明实践能力得分,若想学期总成绩不低于分,则纸笔测试的成绩至少是 .
三、解答题
14.某校在一次演讲比赛中,甲,乙的各项得分如表.
演讲内容 语言表达 临场表现
甲 90 85 80
乙 84 83 91
(1)如果根据三项得分的平均分从高到低确定名次,那么两位同学的排名顺序怎样?
(2)若学校认为这三个项目的重要程度有所不同,而给予“演讲内容”“语言表达”“临场表现”三个项目在总分中的占比为,那么两位同学的排名顺序又怎样?
15.某校随机抽取若干名八年级学生进行体能测试,成绩记为分,分,分,分四个等级,将调查结果绘制成如下条形统计图(图1)和扇形统计图(图2).根据图中信息,回答下列问题:
(1)这次一共抽查了几名学生.
(2)求所抽查的学生的平均分数.
(3)该校有名学生,估计该校有多少名学生体能测试成绩不小于分.
16.某班进行“闪亮之星”的推选工作,经过自荐和第一轮筛选后,甲、乙两位同学进入终选.如表为甲、乙两位同学的得分情况.其中人气分的计算方法是:根据班级主科老师和同学的投票结果,老师一票记10分,同学一票记2分,两个分数相加即为人气分.
学生 人气分 学习分 行规分 工作分
老师票数 同学票数 分数
甲 4 20 a 85 95 85
乙 b 25 70 90 92 90
(1)__________,__________;
(2)经全班同学讨论决定,将人气、学习、行规、工作四个方面在总分中所占的比例分别为.经计算,甲同学的最终得分为87分,请你求出乙同学的最终得分,并判断哪位同学当选.
17.某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示.
测试 项目 测试成绩分
甲 乙 丙
笔试
面试
根据录用程序,组织名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐人)如图所示,每得一票记作分.
(1)甲的民主评议得分为 分;如果根据三项测试的平均成绩确定录用人选,那么 将被录用.
(2)根据实际需要,单位将笔试、面试、民主评议三项测试得分按的比例确定个人成绩,那么谁将被录用?(请写出计算过程)
18.某班准备选取一名同学参加校级知识竞赛,需对甲、乙、丙三名候选人进行笔试和口试,并组织全班40名同学民主投票(无弃权且每人只能投1票,每得一票记作2分).测试成绩与得票率分别统计如下:
测试项目 测试成绩(分)
甲 乙 丙
笔试 75 80 84
口试 90 80 80
(1)请算出三人的得票分.
(2)通过计算说明根据笔试、口试、投票三项得分的平均数是否可确定人选.
(3)如果将笔试,口试,投票三项得分按,,计入个人成绩,请说明谁将被选中.
试卷第1页,共3页
试卷第1页,共3页
《3.1平均数同步练习—2024—2025学年浙教版八年级下册》参考答案
题号 1 2 3 4 5 6 7 8
答案 C B B B B A D B
1.C
【分析】本题考查了求一组数的平均数,根据求平均数的公式列式计算,即可作答.
【详解】解:∵参展的彩铅、水墨、水彩、速写四个类别作品幅数分别为:58,56,58,60,
∴,
∴这组数据的平均数为58,
故选:C.
2.B
【分析】本题考查了加权平均数,根据加权平均数的计算方法计算即可,解题的关键是明确加权平均数的计算方法.
【详解】解:由题意可得,
小明这学期的体育成绩为分,
故选:.
3.B
【分析】本题考查加权平均数,根据题意和加权平均数的计算方法,可以计算出八(1)班四项综合得分(满分100),本题得以解决.
【详解】解:(分),
即八(1)班四项综合得分(满分100)为分,
故选:B.
4.B
【分析】本题主要考查了分式方程的应用,平均数,先根据平均值等于21列出方程,再求出解,检验可得答案.
【详解】根据题意,得
,
解得.
经检验,是原方程的根.
所以,x的值是4.
故选:B.
5.B
【分析】根据数据,,,,的平均数为可知,据此可得出的值.
【详解】解:数据,,,,的平均数为,
,
,
数据,,,,的平均数为.
故选:B.
【点睛】此题主要考查了平均数,熟记平均数是解答此题的关键.
6.A
【分析】本题考查的是加权平均数的含义,直接利用加权平均数的含义计算即可.
【详解】解:平均成绩为:
(分).
故选 A.
7.D
【分析】根据平均数的定义列出方程求解可得;
【详解】∵一组数据 的平均数为
解得:
故选D
【点睛】本题主要考查算术平均数,解题的关键是熟练掌握平均数的定义;平均数是指在一组数据中所有数据之和再除以数据的个数;它是反映数据集中趋势的一项指标
8.B
【分析】根据题意可知:“地面”最重要,“黑板”次之,“门窗”要求最低,再观察各个选项,可得答案.
【详解】解:“地面”最重要,“黑板”次之,“门窗”要求最低,
对地面、黑板、门窗三项考察比较合适的比例设计分别为,,,
故选:B.
【点睛】本题主要考查了加权平均数,解答本题的关键是明确权的意义.
9.4
【分析】本题主要考查了平均数,根据平均数的定义即可求解,熟练掌握平均数是指在一组数据中所有数据之和再除以数据的个数是解决此题的关键.
【详解】解:∵个数,,…的平均数是,
,
,
,,…….,平均数
,
故答案为:4.
10.乙
【分析】本题考查加权平均数,解答本题的关键是明确题意,求出相应的加权平均数.根据表格中的数据和加权平均数的计算方法,可以分别求出甲、乙、丙的成绩,然后比较大小即可.
【详解】解:由题意可得,
甲的成绩为:
乙的成绩为:
丙的成绩为:
∵,
∴乙将被录取,
故答案为:乙.
11.
【分析】本题考查了平均数.由题意知,,,,,的和为,则可计算出,,,的和,除以10,即为新数据的平均数.
【详解】解:,,,,的平均数为
,,,的平均数.
故答案为:.
12.
【分析】本题考查了加权平均数的求法,根据加权平均数的计算方法列式进行计算是解题的关键.
【详解】解:小王的最终成绩为分,
故答案为:.
13.分
【分析】本题考查了加权平均数、一元一次不等式的应用,设小明的纸笔测试的成绩是分,根据加权平均数列出不等式,求解即可,熟练掌握加权平均数、正确列出一元一次不等式是解题的关键.
【详解】解:设小明的纸笔测试的成绩是分,
由题意得:
解得:,
∴纸笔测试的成绩至少是分,
故答案为:分.
14.(1)根据三项得分的平均数从高到低确定名次,乙第一,甲第二
(2)两个的排名顺序发生变化,甲第一,乙第二
【分析】本题考查算术平均数、加权平均数的意义及计算方法,体会“权”在求平均数时的作用.
(1)根据算术平均数的计算方法计算甲、乙的平均数,通过比较得出得出结论.
(2)利用加权平均数的计算方法分别计算甲、乙的总评成绩,比较做出判断即可.
【详解】(1)解:甲的算术平均数:,
乙的算术平均数:.
因此第一名是乙,第二名是甲,
答:根据三项得分的平均数从高到低确定名次,乙第一,甲第二.
(2)解:甲班的总评成绩:,
乙班的总评成绩:,
,
∴甲高于乙,
答:两个的排名顺序发生变化,甲第一,乙第二.
15.(1)名
(2)分
(3)名
【分析】本题考查了条形统计图,扇形统计图,求平均数,用样本估计总体;读懂统计图,从不同的统计图中得到必要的信息是解答本题的关键.
(1)根据“分”的人数除以其占调查人数的比例,即可求出调查人数;
(2)先求出“分”和“分”的人数,再根据平均数是指在一组数据中所有数据之和再除以数据的个数,计算即可;
(3)用总人数乘以“分”和“分”占调查人数的比例,即可求解.
【详解】(1)解:依题意得,“分”的人数有人,占调查人数的,
∴共抽取学生(人);
故这次一共抽查了名学生.
(2)解:“分”的人数占调查人数的,
∴“分”的人数为:(人),
“分”的人数为:(人),
抽取的所有学生成绩的平均数是:(分).
故抽取的所有学生成绩的平均数为分.
(3)解:(人),
故估计该校有名学生体能测试成绩不小于分.
16.(1)80;2;
(2)乙的得分为分,甲同学当选
【分析】本题主要考查了有理数的四则运算,求加权平均数:
(1)根据表格中的数据以及老师一票记10分,同学一票记2分进行列式求解即可;
(2)根据加权平均数的求解方法求解即可.
【详解】(1)解:由题意得,,,
故答案为:80;2;
(2)解:乙的最终得分为分,
∵,
∴甲同学当选.
17.(1),乙
(2)丙将被录用
【分析】(1)根据扇形统计图得出每部分所占的百分比,求出甲、乙、丙民主评议的得分,再根据平均数的计算公式求出各自的平均数,然后进行比较,即可得出答案;
(2)利用加权平均数的计算公式列式计算求出三人的得分,然后即可判断录用的候选人.
【详解】(1)解:甲的民主评议得分为:(分,
乙的民主评议得分为:(分,
丙的民主评议得分为:(分,
甲的平均成绩是:(分,
乙的平均成绩是:(分,
丙的平均成绩是:(分,
根据三项测试的平均成绩确定录用人选,那么乙被录用;
故答案为:50,乙;
(2)解:将笔试、面试、民主评议三项测试得分按的比例,
则甲得分:(分,
乙得分:(分,
丙得分:(分,
则丙将被录用.
【点睛】本题考查的是加权平均数的求法,要注意各部分的权重与相应的数据的关系,根据公式列出算式是解题的关键.
18.(1)甲20分,乙32分,丙28分
(2)无法确定人选
(3)丙被选中
【分析】(1)根据得票数,求出三人的得票分即可;
(2)分别算出甲、乙、丙三人的平均分,进行判断即可;
(3)分别算出三个人的加权平均数,然后进行判断即可.
【详解】(1)解:甲的得票分为:(分),
乙的得票分为:(分),
丙的得票分为:(分).
(2)解:甲的平均分为:(分),
乙的平均分为:(分),
丙的平均分为:(分),
∵乙和丙的平均分相同,
∴无法确定人选.
(3)解:甲:(分).
乙:(分).
丙:(分).
∴丙被选中.
【点睛】本题主要考查了加权平均数的计算,利用平均数和加权平均数做决策,解题的关键是准确求出平均数和加权平均数.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
