3.3方差和标准差同步练习(含解析)2024—2025学年浙教版八年级下册
文档属性
| 名称 | 3.3方差和标准差同步练习(含解析)2024—2025学年浙教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 450.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-21 00:00:00 | ||
图片预览



文档简介
3.3方差和标准差同步练习—2024—2025学年浙教版八年级下册
一、单选题
1.已知一个样本数据为2,3,4,5,6,则这组数据的方差和标准差分别是( )
A.2、 B.3、 C.、 2 D.、3
2.已知数据,,,的方差是4,则一组新数据,,,的方差是( )
A.4 B.5 C.9 D.16
3.水果超市售卖一批散装苹果,苹果大小不一,某顾客从中选购了部分大小均匀的苹果.设原有苹果质量(单位:)的方差为,该顾客选购的苹果质量的方差为,则与的大小关系是( ).
A. B.
C. D.它们的大小关系不确定
4.甲、乙、丙、丁四名射击运动员参加射击预选赛,每人射击20发子弹.他们射击成绩的平均数及标准差如表所示.
人员成绩 甲 乙 丙 丁
平均数(环) 8.6 8.6 9.2 9.2
标准差S(环) 1.3 1.5 1.0 1.2
若要选一名成绩较好且又稳定的运动员参赛,则应选运动员( )
A.甲 B.乙 C.丙 D.丁
5.九年级某班30位同学的体育素质测试成绩统计如表所示,其中两个数据被遮盖,下列关于成绩的统计量中,与被遮盖的数据无关的是( )
成绩 24 25 26 27 28 29 30
人数 ■ ■ 2 3 6 7 9
A.平均数,方差 B.中位数,方差 C.中位数,众数 D.平均数,众数
6.如图,一个转盘被分成4等分,每份内均标有数字,旋转这转盘5次,得到5个数字,经统计这列数的平均数为2,下列判断正确的是( )
A.中位数一定是2 B.众数一定是2
C.方差一定小于2 D.方差一定大于1
7.设数据0,1,2,3,4的平均数为a,中位数为b,方差为c,则( )
A. B. C. D.
8.李老师统计八(5)班40位学生的数学成绩(均为不同整数),错将最高分写低了1分,则一定不受影响的统计量是( )
A.中位数 B.方差 C.众数 D.平均数
二、填空题
9.一组数据:,这组数据的方差是 .
10.如果一组数据,,,的方差是5,则另一组数据,,…,的方差是 .
11.已知某组数据的方差为,则的值为 .
12.下列五个数:11,12,13,14,15的标准差为 .
13.已知一组数据1,2,8,x,7,4的众数为2,则x的值是 ,这组数据的标准差是 .
三、解答题
14.我市某中学八年级举行“中国梦·校园好声音”歌手大赛,其中八年级(1)、八年级(2)班派出的名选手的比赛成绩如图所示:
(1)根据图,完成表格:
中位数(分) 众数(分) 平均数(分)
班
班
(2)请问,哪个班参加比赛选手的成绩比较整齐?为什么?
15.某校舞蹈队共16名学生,测量并获取了所有学生的身高(单位:cm),数据整理如下:
.16名学生的身高:
161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,175
.16名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
166.75
(1)写出表中,的值;
(2)对于不同组的学生,如果一组学生的身高的方差越小,则认为该组舞台呈现效果越好.据此推断:在下列两组学生中,舞台呈现效果更好的是______.(填“甲组”或“乙组”);
甲组学生的身高 162 165 165 166 166
乙组学生的身高 161 162 164 165 175
(3)该舞蹈队要选五名学生参加比赛.已确定三名学生参赛,他们的身高分别为168,168,172,他们的身高的方差为,在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差变小,其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为______和______.
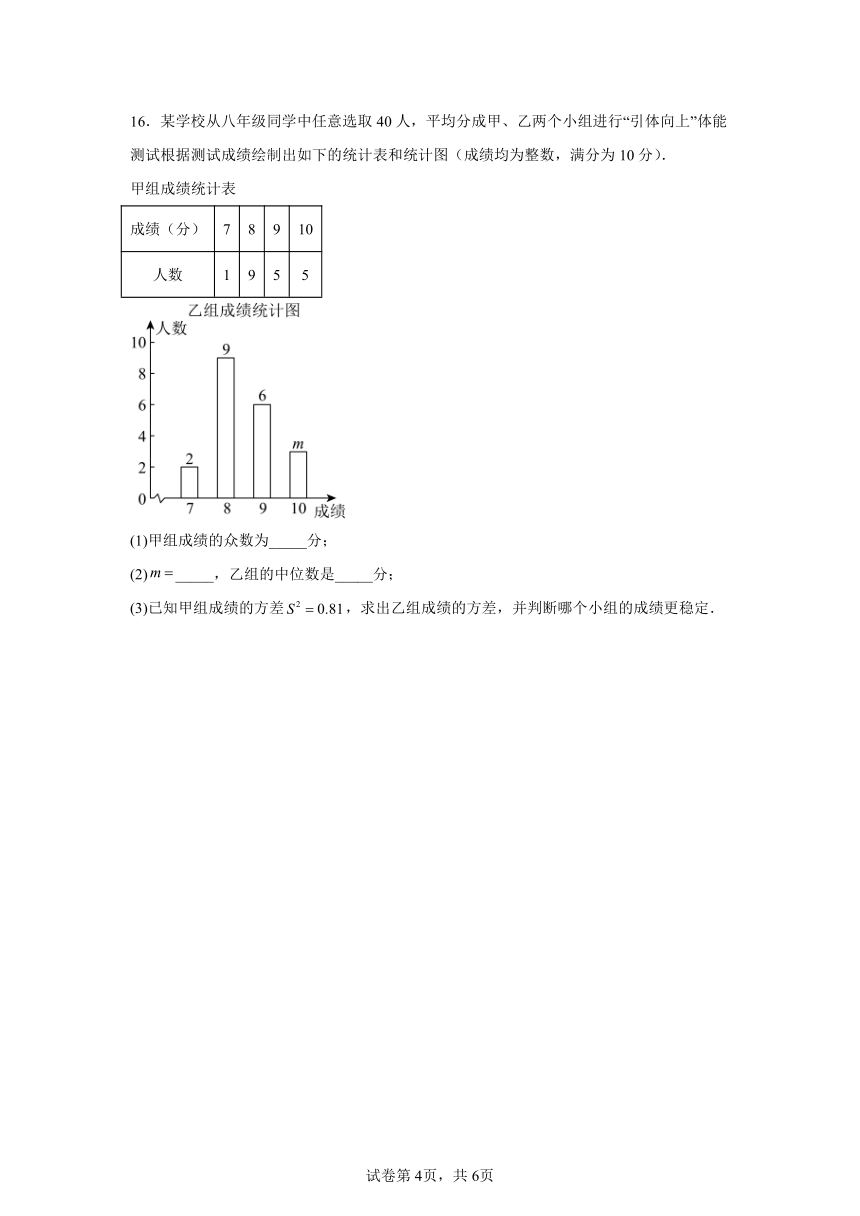
16.某学校从八年级同学中任意选取40人,平均分成甲、乙两个小组进行“引体向上”体能测试根据测试成绩绘制出如下的统计表和统计图(成绩均为整数,满分为10分).
甲组成绩统计表
成绩(分) 7 8 9 10
人数 1 9 5 5
(1)甲组成绩的众数为_____分;
(2)_____,乙组的中位数是_____分;
(3)已知甲组成绩的方差,求出乙组成绩的方差,并判断哪个小组的成绩更稳定.
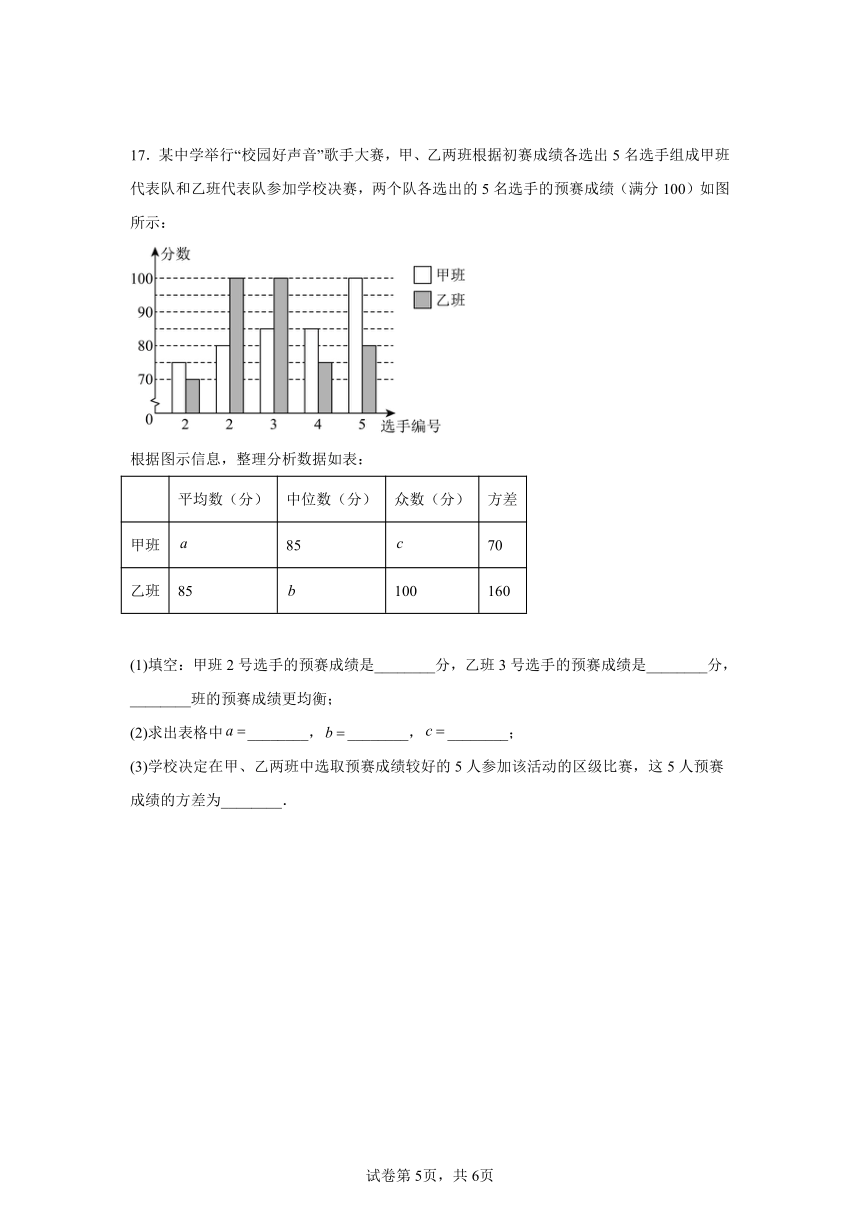
17.某中学举行“校园好声音”歌手大赛,甲、乙两班根据初赛成绩各选出5名选手组成甲班代表队和乙班代表队参加学校决赛,两个队各选出的5名选手的预赛成绩(满分100)如图所示:
根据图示信息,整理分析数据如表:
平均数(分) 中位数(分) 众数(分) 方差
甲班 85 70
乙班 85 100 160
(1)填空:甲班2号选手的预赛成绩是________分,乙班3号选手的预赛成绩是________分,________班的预赛成绩更均衡;
(2)求出表格中________,________,________;
(3)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,这5人预赛成绩的方差为________.
18.某中学举行“中国梦.校园好声音”歌手大赛,八(1)、八(2)班根据初赛成绩,两个班各选出的5名选手的决赛成绩如图表.
平均数/分 中位数/分 众数/分
八(1) a 85 c
八(2) 85 b 100
(1)写出上表中a、b、c的值;
(2)结合两个班成绩的平均数和中位数,分析哪个班的决赛成绩较好?
(3)计算两个班决赛成绩的方差,并判断哪个班代表队选手的成绩较为稳定.
试卷第1页,共3页
试卷第1页,共3页
《3.3方差和标准差同步练习—2024—2025学年浙教版八年级下册》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D B C C C A A
1.A
【分析】此题考查计算方差和标准差,熟练掌握计算公式是解题的关键,先求出数据的平均数,再根据方差及标准差公式求出方差.
【详解】解:这组数据的平均数,
方差,
标准差,
故选:A.
2.D
【分析】 本题考查方差的性质.先设这组数据的平均数为,则另一组新数据的平均数为,方差为,代入公式进行推导可求出答案.
【详解】解:设这组数据的平均数为,则另一组新数据的平均数为,
∵,
∴
=
=
,
故选:D.
3.B
【分析】本题主要考查了方差与波动性之间的关系,方差是反映一组数据的波动大小的一个量,方差越大,数据波动越大,稳定性越小,而根据题意可得顾客选购苹果的质量比水果超市的波动较小,据此可得答案.
【详解】解:∵水果超市的苹果大小不一,而该顾客选购大小均匀的苹果,
∴说明顾客选购苹果的质量比水果超市的波动较小,
∴超市苹果质量的方差大于顾客选购苹果的方差,即,
故选:B.
4.C
【分析】本题考查标准差、方差和算术平均数,掌握方差反映了一组数据的波动大小,方差越大,波动越大,方差越小,数据越稳定是解题的关键.先比较平均数,再比较标准差,然后得出丙的方差小于丁的方差,从而得出答案.
【详解】解:由图可知,丙和丁的平均成绩好,
∵丙的标准差小于丁的标准差,
∴丙的方差小于丁的方差,
∴若要选一名成绩较好且发挥稳定的运动员参赛,则应选择丙,
故选:C.
5.C
【分析】本题主要考查统计量的选择,根据众数和中位数的定义求解可得,解题的关键是掌握众数和中位数的概念.
【详解】解:这组数据中成绩为24、25的人数和为,
则这组数据中出现次数最多的数30,即众数30,
第15、16个数据都是29,
则中位数为29,
∴与被遮盖的数据无关的是中位数,众数.
故选:C.
6.C
【分析】本题考查了中位数、众数、平均数、方差,根据中位数、众数、方差的定义判断即可得出答案.
【详解】解:当这列数为1,1,1,3,4时,平均数为,中位数为,众数为1,方差为,故A、B不符合题意;
当这列数为2,2,2,2,2时,平均数为,中位数为2,众数为2,方差为,故D不符合题意;
故选:C.
7.A
【分析】该题主要考查了平均数、中位数、方差的计算,解题的关键是掌握平均数、中位数、方差的计算公式.
根据的值解答即可.
【详解】解:平均数;
数据中,中间的数是2,
∴中位数;
方差.
,
故选:A.
8.A
【分析】本题主要考查了中位数、方差、众数、平均数,根据中位数、方差、众数、平均数的定义逐项判断即可得出答案.
【详解】解:A、成绩按照由高到低排列,中位数是第20、21个数值的平均数,与最大的数值无关,选项说法正确,符合题意;
B、方差的计算与每一个数值都有关,故方差发生变化,选项说法错误,不符合题意;
C、众数与每一个数值都有关,故众数可能发生变化,选项说法错误,不符合题意;
D、平均数的计算与每一个数值都有关,故平均数发生变化,选项说法错误,不符合题意;
故选:A.
9.
【分析】本题考查了数据的方差,先求出数据的平均数,再根据方差公式计算即可求解,掌握方差计算公式是解题的关键.
【详解】解:数据的平均数,
∴,
故答案为:.
10.20
【分析】本题考查了方差的定义.当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数(或除以一个数)时,平均数也乘以或除以这个数,方差变为这个数的平方倍.根据方差定义去化简计算即可.
【详解】
解:记,,,的平均数为,则,
数据,,…,的平均数为,
由题意得,,
∴数据,,…,的方差为
;
故答案为:20.
11.
【分析】本题主要考查方差和算术平均数的定义.由题意知,这组数据为3、4、7、10,再根据平均数的定义求解即可.
【详解】解:由题意知,这组数据为3、4、7、10,
所以这组数据的平均数为,即的值为
故答案为:6.
12.
【分析】此题考查了标准差.先求出它们的方差,再求出标准差即可.
【详解】解:这五个数的平均数为:,
方差
,
故标准差为.
故答案为:.
13.
【分析】本题考查了标准差,根据众数定义求得x的值,掌握方差、标准差的计算公式是解题的关键.先根据众数的定义求出x的值,再求出平均数,继而根据方差公式计算方差,然后求出标准差即可.
【详解】解:∵1,2,8,x,7,4的众数为2,
∴,
∴这组数据的平均数是,
则方差为
.
∴标准差为;
故答案为:,.
14.(1)表见详解
(2)八(1)班参加比赛选手的成绩比较整齐,理由见详解
【分析】(1)根据条形统计图给出的数据,把这组数据从小到大排列,找出最中间的数求出中位数,再根据众数、平均数的定义即可得出答案;
(2)根据方差的公式计算可得出两个班的方差,根据平均数和方差,再进行比较即可得出答案.
【详解】(1)解:∵八(1)的成绩分别是,把这组数据从小到大排列为,
∴这组数据的中位数是分,众数是分,平均数分;
∵八(2)的成绩分别是,把这组数据从小到大排列为,
∴这组数据的众数是90分,
填表如下:
中位数(分) 众数(分) 平均数(分)
班
班
(2)解:八(1)班参加比赛选手的成绩比较整齐;
理由如下:八(1)的成绩的方差为;
八(2)的成绩的方差;
∵两个班的平均分相同,均为,八(1)班的方差小,,
∴八(1)班选手的成绩总体上较整齐.
【点睛】此题考查了平均数、中位数、方差.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,熟练掌握以上知识是解题的关键.
15.(1)166,165
(2)甲组
(3)
【分析】本题考查了平均数、众数、中位数和方差,熟记方差的计算公式以及方差的意义是解题的关键.
(1)根据众数和中位数的定义进行计算;
(2)根据方差的计算公式计算方差,然后根据方差的意义进行比较;
(3)根据方差进行比较.
【详解】(1)解:数据按由小到大的顺序排序:161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,175,
则舞蹈队16名学生身高的中位数为,
数据165最多,所以,众数为,
故答案为:166,165;
(2)解:甲组学生身高的平均值是:,
甲组学生身高的方差是:,
乙组学生身高的平均值是:,
乙组学生身高的方差是:,
∵,
∴甲组舞台呈现效果更好.
故答案为:甲组;
(3)解:∵168,168,172的平均数为,
方差,
又所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,
∴数据的差别较小,
可供选择的有
平均数为:,
方差为:,
∴选出的另外两名学生的身高分别为和,
故答案为:.
16.(1)8
(2)3,8
(3),乙组的成绩更加稳定
【分析】本题考查了平均数、众数和方差的有关内容,解题的关键是正确理解统计图.
(1)用总人数减去其他成绩的人数,即可求出;
(2)根据中位数和众数的定义即可求出甲组成绩的众数和乙组成绩的中位数;
(3)先求出乙组的平均数,再根据方差公式求出乙组的方差,然后进行比较,即可得出答案.
【详解】(1)解:甲组成绩出现次数最多的是8,则甲组成绩的众数是8,
故答案为:8;
(2)解:(人),
乙组成绩的中位数是第10、11个数的平均数,则中位数是:,
故答案为:3,8;
(3)解:乙组平均成绩是:(分),
乙组的方差是:;
,
乙组的成绩更加稳定.
17.(1),,甲
(2),,
(3)
【分析】(1)根据条形统计图即可得到甲班2号选手、乙班3号选手的预赛成绩,比较两个班成绩的方差,方差比较小的班级成绩更均衡;
(2)先分别根据条形统计图确定甲、乙两个班选手的成绩,根据平均数、中位数、众数的定义和计算公式计算,即可解题;
(3)先确定10名选手中成绩最好的5名同学成绩,根据平均数的意义求出平均数,再根据平均数求出方差即可.
【详解】(1)解:由条形统计图可知::甲班2号选手的预赛成绩是分,乙班3号选手的预赛成绩是分,
由表可知:甲班方差乙班方差,
甲班的预赛成绩更均衡;
故答案为:,,甲;
(2)解:由条形统计图可知:甲班成绩为、、、、,
甲班平均数,
甲班数据中其中出现次数最多,为两次,故甲班众数,
由条形统计图可知:乙班成绩为、、、、,
从小到大排序为:、、、、,
乙班中位数,
故答案为:,,;
(3)解:由条形统计图可知:预赛成绩较好的5人成绩为、、、、,
这5人预赛成绩的平均数为,
这5人预赛成绩的方差为,
故答案为:.
【点睛】本题考查了根据条形统计图提取数据,平均数,中位数、众数、方差的意义和计算方法等知识,熟知相关概念,根据统计图正确提取相关信息是解题关键.
18.(1)
(2)八(1)班成绩好些
(3)八(1)班代表队选手的成绩较为稳定
【分析】本题考查方差的定义:一般地设个数据,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
(1)根据平均数的计算公式和众数、中位数的定义分别进行解答,然后把表补充完整即可;
(2)根据平均数相同的情况下,中位数高的那个队的决赛成绩较好;
(3)根据方差公式先算出各队的方差,然后根据方差的意义即可得出答案.
【详解】(1)解:八(1)班的平均成绩是:(分),
在八(1)班成绩中85出现了2次,出现的次数最多;(分),
把八(2)班的成绩从小到大排列为:70,75,80,100,100,最中间的数是80,则中位数(分);
故:;
(2)解:八(1)班成绩好些,
因为两个队的平均数都相同,八(1)班的中位数高,
所以在平均数相同的情况下,中位数高的八(1)班成绩好些;
(3)解:八(1)班的方差是:,
八(2)班的方差是:,
∵,
∴八(1)班代表队选手的成绩较为稳定.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知一个样本数据为2,3,4,5,6,则这组数据的方差和标准差分别是( )
A.2、 B.3、 C.、 2 D.、3
2.已知数据,,,的方差是4,则一组新数据,,,的方差是( )
A.4 B.5 C.9 D.16
3.水果超市售卖一批散装苹果,苹果大小不一,某顾客从中选购了部分大小均匀的苹果.设原有苹果质量(单位:)的方差为,该顾客选购的苹果质量的方差为,则与的大小关系是( ).
A. B.
C. D.它们的大小关系不确定
4.甲、乙、丙、丁四名射击运动员参加射击预选赛,每人射击20发子弹.他们射击成绩的平均数及标准差如表所示.
人员成绩 甲 乙 丙 丁
平均数(环) 8.6 8.6 9.2 9.2
标准差S(环) 1.3 1.5 1.0 1.2
若要选一名成绩较好且又稳定的运动员参赛,则应选运动员( )
A.甲 B.乙 C.丙 D.丁
5.九年级某班30位同学的体育素质测试成绩统计如表所示,其中两个数据被遮盖,下列关于成绩的统计量中,与被遮盖的数据无关的是( )
成绩 24 25 26 27 28 29 30
人数 ■ ■ 2 3 6 7 9
A.平均数,方差 B.中位数,方差 C.中位数,众数 D.平均数,众数
6.如图,一个转盘被分成4等分,每份内均标有数字,旋转这转盘5次,得到5个数字,经统计这列数的平均数为2,下列判断正确的是( )
A.中位数一定是2 B.众数一定是2
C.方差一定小于2 D.方差一定大于1
7.设数据0,1,2,3,4的平均数为a,中位数为b,方差为c,则( )
A. B. C. D.
8.李老师统计八(5)班40位学生的数学成绩(均为不同整数),错将最高分写低了1分,则一定不受影响的统计量是( )
A.中位数 B.方差 C.众数 D.平均数
二、填空题
9.一组数据:,这组数据的方差是 .
10.如果一组数据,,,的方差是5,则另一组数据,,…,的方差是 .
11.已知某组数据的方差为,则的值为 .
12.下列五个数:11,12,13,14,15的标准差为 .
13.已知一组数据1,2,8,x,7,4的众数为2,则x的值是 ,这组数据的标准差是 .
三、解答题
14.我市某中学八年级举行“中国梦·校园好声音”歌手大赛,其中八年级(1)、八年级(2)班派出的名选手的比赛成绩如图所示:
(1)根据图,完成表格:
中位数(分) 众数(分) 平均数(分)
班
班
(2)请问,哪个班参加比赛选手的成绩比较整齐?为什么?
15.某校舞蹈队共16名学生,测量并获取了所有学生的身高(单位:cm),数据整理如下:
.16名学生的身高:
161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,175
.16名学生的身高的平均数、中位数、众数:
平均数 中位数 众数
166.75
(1)写出表中,的值;
(2)对于不同组的学生,如果一组学生的身高的方差越小,则认为该组舞台呈现效果越好.据此推断:在下列两组学生中,舞台呈现效果更好的是______.(填“甲组”或“乙组”);
甲组学生的身高 162 165 165 166 166
乙组学生的身高 161 162 164 165 175
(3)该舞蹈队要选五名学生参加比赛.已确定三名学生参赛,他们的身高分别为168,168,172,他们的身高的方差为,在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差变小,其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为______和______.
16.某学校从八年级同学中任意选取40人,平均分成甲、乙两个小组进行“引体向上”体能测试根据测试成绩绘制出如下的统计表和统计图(成绩均为整数,满分为10分).
甲组成绩统计表
成绩(分) 7 8 9 10
人数 1 9 5 5
(1)甲组成绩的众数为_____分;
(2)_____,乙组的中位数是_____分;
(3)已知甲组成绩的方差,求出乙组成绩的方差,并判断哪个小组的成绩更稳定.
17.某中学举行“校园好声音”歌手大赛,甲、乙两班根据初赛成绩各选出5名选手组成甲班代表队和乙班代表队参加学校决赛,两个队各选出的5名选手的预赛成绩(满分100)如图所示:
根据图示信息,整理分析数据如表:
平均数(分) 中位数(分) 众数(分) 方差
甲班 85 70
乙班 85 100 160
(1)填空:甲班2号选手的预赛成绩是________分,乙班3号选手的预赛成绩是________分,________班的预赛成绩更均衡;
(2)求出表格中________,________,________;
(3)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的区级比赛,这5人预赛成绩的方差为________.
18.某中学举行“中国梦.校园好声音”歌手大赛,八(1)、八(2)班根据初赛成绩,两个班各选出的5名选手的决赛成绩如图表.
平均数/分 中位数/分 众数/分
八(1) a 85 c
八(2) 85 b 100
(1)写出上表中a、b、c的值;
(2)结合两个班成绩的平均数和中位数,分析哪个班的决赛成绩较好?
(3)计算两个班决赛成绩的方差,并判断哪个班代表队选手的成绩较为稳定.
试卷第1页,共3页
试卷第1页,共3页
《3.3方差和标准差同步练习—2024—2025学年浙教版八年级下册》参考答案
题号 1 2 3 4 5 6 7 8
答案 A D B C C C A A
1.A
【分析】此题考查计算方差和标准差,熟练掌握计算公式是解题的关键,先求出数据的平均数,再根据方差及标准差公式求出方差.
【详解】解:这组数据的平均数,
方差,
标准差,
故选:A.
2.D
【分析】 本题考查方差的性质.先设这组数据的平均数为,则另一组新数据的平均数为,方差为,代入公式进行推导可求出答案.
【详解】解:设这组数据的平均数为,则另一组新数据的平均数为,
∵,
∴
=
=
,
故选:D.
3.B
【分析】本题主要考查了方差与波动性之间的关系,方差是反映一组数据的波动大小的一个量,方差越大,数据波动越大,稳定性越小,而根据题意可得顾客选购苹果的质量比水果超市的波动较小,据此可得答案.
【详解】解:∵水果超市的苹果大小不一,而该顾客选购大小均匀的苹果,
∴说明顾客选购苹果的质量比水果超市的波动较小,
∴超市苹果质量的方差大于顾客选购苹果的方差,即,
故选:B.
4.C
【分析】本题考查标准差、方差和算术平均数,掌握方差反映了一组数据的波动大小,方差越大,波动越大,方差越小,数据越稳定是解题的关键.先比较平均数,再比较标准差,然后得出丙的方差小于丁的方差,从而得出答案.
【详解】解:由图可知,丙和丁的平均成绩好,
∵丙的标准差小于丁的标准差,
∴丙的方差小于丁的方差,
∴若要选一名成绩较好且发挥稳定的运动员参赛,则应选择丙,
故选:C.
5.C
【分析】本题主要考查统计量的选择,根据众数和中位数的定义求解可得,解题的关键是掌握众数和中位数的概念.
【详解】解:这组数据中成绩为24、25的人数和为,
则这组数据中出现次数最多的数30,即众数30,
第15、16个数据都是29,
则中位数为29,
∴与被遮盖的数据无关的是中位数,众数.
故选:C.
6.C
【分析】本题考查了中位数、众数、平均数、方差,根据中位数、众数、方差的定义判断即可得出答案.
【详解】解:当这列数为1,1,1,3,4时,平均数为,中位数为,众数为1,方差为,故A、B不符合题意;
当这列数为2,2,2,2,2时,平均数为,中位数为2,众数为2,方差为,故D不符合题意;
故选:C.
7.A
【分析】该题主要考查了平均数、中位数、方差的计算,解题的关键是掌握平均数、中位数、方差的计算公式.
根据的值解答即可.
【详解】解:平均数;
数据中,中间的数是2,
∴中位数;
方差.
,
故选:A.
8.A
【分析】本题主要考查了中位数、方差、众数、平均数,根据中位数、方差、众数、平均数的定义逐项判断即可得出答案.
【详解】解:A、成绩按照由高到低排列,中位数是第20、21个数值的平均数,与最大的数值无关,选项说法正确,符合题意;
B、方差的计算与每一个数值都有关,故方差发生变化,选项说法错误,不符合题意;
C、众数与每一个数值都有关,故众数可能发生变化,选项说法错误,不符合题意;
D、平均数的计算与每一个数值都有关,故平均数发生变化,选项说法错误,不符合题意;
故选:A.
9.
【分析】本题考查了数据的方差,先求出数据的平均数,再根据方差公式计算即可求解,掌握方差计算公式是解题的关键.
【详解】解:数据的平均数,
∴,
故答案为:.
10.20
【分析】本题考查了方差的定义.当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数(或除以一个数)时,平均数也乘以或除以这个数,方差变为这个数的平方倍.根据方差定义去化简计算即可.
【详解】
解:记,,,的平均数为,则,
数据,,…,的平均数为,
由题意得,,
∴数据,,…,的方差为
;
故答案为:20.
11.
【分析】本题主要考查方差和算术平均数的定义.由题意知,这组数据为3、4、7、10,再根据平均数的定义求解即可.
【详解】解:由题意知,这组数据为3、4、7、10,
所以这组数据的平均数为,即的值为
故答案为:6.
12.
【分析】此题考查了标准差.先求出它们的方差,再求出标准差即可.
【详解】解:这五个数的平均数为:,
方差
,
故标准差为.
故答案为:.
13.
【分析】本题考查了标准差,根据众数定义求得x的值,掌握方差、标准差的计算公式是解题的关键.先根据众数的定义求出x的值,再求出平均数,继而根据方差公式计算方差,然后求出标准差即可.
【详解】解:∵1,2,8,x,7,4的众数为2,
∴,
∴这组数据的平均数是,
则方差为
.
∴标准差为;
故答案为:,.
14.(1)表见详解
(2)八(1)班参加比赛选手的成绩比较整齐,理由见详解
【分析】(1)根据条形统计图给出的数据,把这组数据从小到大排列,找出最中间的数求出中位数,再根据众数、平均数的定义即可得出答案;
(2)根据方差的公式计算可得出两个班的方差,根据平均数和方差,再进行比较即可得出答案.
【详解】(1)解:∵八(1)的成绩分别是,把这组数据从小到大排列为,
∴这组数据的中位数是分,众数是分,平均数分;
∵八(2)的成绩分别是,把这组数据从小到大排列为,
∴这组数据的众数是90分,
填表如下:
中位数(分) 众数(分) 平均数(分)
班
班
(2)解:八(1)班参加比赛选手的成绩比较整齐;
理由如下:八(1)的成绩的方差为;
八(2)的成绩的方差;
∵两个班的平均分相同,均为,八(1)班的方差小,,
∴八(1)班选手的成绩总体上较整齐.
【点睛】此题考查了平均数、中位数、方差.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定,熟练掌握以上知识是解题的关键.
15.(1)166,165
(2)甲组
(3)
【分析】本题考查了平均数、众数、中位数和方差,熟记方差的计算公式以及方差的意义是解题的关键.
(1)根据众数和中位数的定义进行计算;
(2)根据方差的计算公式计算方差,然后根据方差的意义进行比较;
(3)根据方差进行比较.
【详解】(1)解:数据按由小到大的顺序排序:161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,175,
则舞蹈队16名学生身高的中位数为,
数据165最多,所以,众数为,
故答案为:166,165;
(2)解:甲组学生身高的平均值是:,
甲组学生身高的方差是:,
乙组学生身高的平均值是:,
乙组学生身高的方差是:,
∵,
∴甲组舞台呈现效果更好.
故答案为:甲组;
(3)解:∵168,168,172的平均数为,
方差,
又所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,
∴数据的差别较小,
可供选择的有
平均数为:,
方差为:,
∴选出的另外两名学生的身高分别为和,
故答案为:.
16.(1)8
(2)3,8
(3),乙组的成绩更加稳定
【分析】本题考查了平均数、众数和方差的有关内容,解题的关键是正确理解统计图.
(1)用总人数减去其他成绩的人数,即可求出;
(2)根据中位数和众数的定义即可求出甲组成绩的众数和乙组成绩的中位数;
(3)先求出乙组的平均数,再根据方差公式求出乙组的方差,然后进行比较,即可得出答案.
【详解】(1)解:甲组成绩出现次数最多的是8,则甲组成绩的众数是8,
故答案为:8;
(2)解:(人),
乙组成绩的中位数是第10、11个数的平均数,则中位数是:,
故答案为:3,8;
(3)解:乙组平均成绩是:(分),
乙组的方差是:;
,
乙组的成绩更加稳定.
17.(1),,甲
(2),,
(3)
【分析】(1)根据条形统计图即可得到甲班2号选手、乙班3号选手的预赛成绩,比较两个班成绩的方差,方差比较小的班级成绩更均衡;
(2)先分别根据条形统计图确定甲、乙两个班选手的成绩,根据平均数、中位数、众数的定义和计算公式计算,即可解题;
(3)先确定10名选手中成绩最好的5名同学成绩,根据平均数的意义求出平均数,再根据平均数求出方差即可.
【详解】(1)解:由条形统计图可知::甲班2号选手的预赛成绩是分,乙班3号选手的预赛成绩是分,
由表可知:甲班方差乙班方差,
甲班的预赛成绩更均衡;
故答案为:,,甲;
(2)解:由条形统计图可知:甲班成绩为、、、、,
甲班平均数,
甲班数据中其中出现次数最多,为两次,故甲班众数,
由条形统计图可知:乙班成绩为、、、、,
从小到大排序为:、、、、,
乙班中位数,
故答案为:,,;
(3)解:由条形统计图可知:预赛成绩较好的5人成绩为、、、、,
这5人预赛成绩的平均数为,
这5人预赛成绩的方差为,
故答案为:.
【点睛】本题考查了根据条形统计图提取数据,平均数,中位数、众数、方差的意义和计算方法等知识,熟知相关概念,根据统计图正确提取相关信息是解题关键.
18.(1)
(2)八(1)班成绩好些
(3)八(1)班代表队选手的成绩较为稳定
【分析】本题考查方差的定义:一般地设个数据,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
(1)根据平均数的计算公式和众数、中位数的定义分别进行解答,然后把表补充完整即可;
(2)根据平均数相同的情况下,中位数高的那个队的决赛成绩较好;
(3)根据方差公式先算出各队的方差,然后根据方差的意义即可得出答案.
【详解】(1)解:八(1)班的平均成绩是:(分),
在八(1)班成绩中85出现了2次,出现的次数最多;(分),
把八(2)班的成绩从小到大排列为:70,75,80,100,100,最中间的数是80,则中位数(分);
故:;
(2)解:八(1)班成绩好些,
因为两个队的平均数都相同,八(1)班的中位数高,
所以在平均数相同的情况下,中位数高的八(1)班成绩好些;
(3)解:八(1)班的方差是:,
八(2)班的方差是:,
∵,
∴八(1)班代表队选手的成绩较为稳定.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
