2.8 直角三角形全等的判定 课件(共11张PPT)
文档属性
| 名称 | 2.8 直角三角形全等的判定 课件(共11张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-23 16:23:07 | ||
图片预览


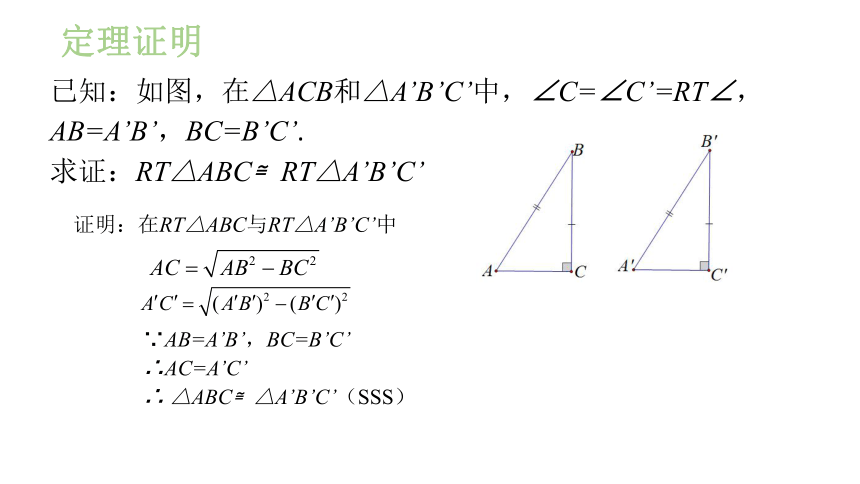
文档简介
(共11张PPT)
浙教版八年级上册第二章
复习回顾
三角形全等的判定方法:
定义:能够重合的两个三角形是全等三角形
基本事实: SSS SAS ASA AAS
复习回顾
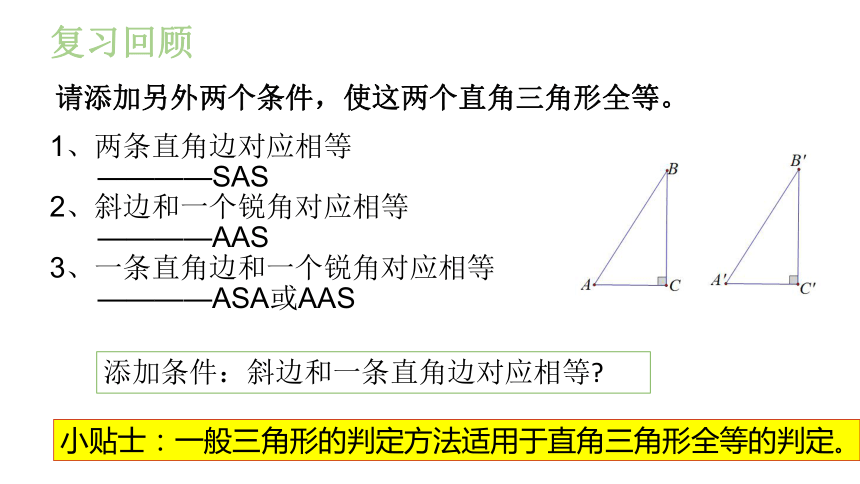
请添加另外两个条件,使这两个直角三角形全等。
1、两条直角边对应相等
————SAS
2、斜边和一个锐角对应相等
————AAS
3、一条直角边和一个锐角对应相等
————ASA或AAS
添加条件:斜边和一条直角边对应相等
小贴士:一般三角形的判定方法适用于直角三角形全等的判定。
新知探究
命题:斜边与一条直角边对应相等的两个直角三角形全等
用画图的方法探究
已知线段a,c(如图),用直尺和圆规作RT△ABC,
使∠C=RT∠,BC=a,AB=c
用你所画的三角形,和其他同学所画的三角形进行比较,它们能重合吗?
定理证明
已知:如图,在△ACB和△A’B’C’中,∠C=∠C’=RT∠,
AB=A’B’,BC=B’C’.
求证:RT△ABC≌RT△A’B’C’
证明:在RT△ABC与RT△A’B’C’中
∵AB=A’B’,BC=B’C’
∴AC=A’C’
∴ △ABC≌△A’B’C’(SSS)
认识定理
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)
几何语言:
在RT△ABC与RT△A’B’C’中
∵AB=A’B’,BC=B’C’(或AC= A C )
∴ RT△ABC≌RT△A’B’C’(HL)
思考:“有两条边相等的两个直角三角形全等”是真命题吗?
定理应用
如图, 在ΔABC中, D是BC的中点, DE⊥ AB于E, DF⊥AC于F, 且DE=DF, 求证:AB=AC.
A
B
C
D
E
F
定理应用
例 已知: 如图, 已知P是∠AOB内一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE, 求证:点P在∠AOB的平分线上.
由此,你能得出什么结论?
几何语言:
∵DP⊥OA,PE⊥OB,且PD=PE
∴OP平分∠AOB
角平分线性质定理的逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上。
定理应用
已知Δ ABC,用直尺和圆规作一点P ,使它到三边距离都相等(要求作出图形,并保留作图痕迹)
知识:
1、尺规作图 ——— 已知斜边和一直角边作直角三角形;
2、“斜边、直角边定理(HL)”;
3、角平分线性质的逆定理。
方法:实验——猜想——验证——推理
课堂小结
浙教版八年级上册第二章
复习回顾
三角形全等的判定方法:
定义:能够重合的两个三角形是全等三角形
基本事实: SSS SAS ASA AAS
复习回顾
请添加另外两个条件,使这两个直角三角形全等。
1、两条直角边对应相等
————SAS
2、斜边和一个锐角对应相等
————AAS
3、一条直角边和一个锐角对应相等
————ASA或AAS
添加条件:斜边和一条直角边对应相等
小贴士:一般三角形的判定方法适用于直角三角形全等的判定。
新知探究
命题:斜边与一条直角边对应相等的两个直角三角形全等
用画图的方法探究
已知线段a,c(如图),用直尺和圆规作RT△ABC,
使∠C=RT∠,BC=a,AB=c
用你所画的三角形,和其他同学所画的三角形进行比较,它们能重合吗?
定理证明
已知:如图,在△ACB和△A’B’C’中,∠C=∠C’=RT∠,
AB=A’B’,BC=B’C’.
求证:RT△ABC≌RT△A’B’C’
证明:在RT△ABC与RT△A’B’C’中
∵AB=A’B’,BC=B’C’
∴AC=A’C’
∴ △ABC≌△A’B’C’(SSS)
认识定理
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)
几何语言:
在RT△ABC与RT△A’B’C’中
∵AB=A’B’,BC=B’C’(或AC= A C )
∴ RT△ABC≌RT△A’B’C’(HL)
思考:“有两条边相等的两个直角三角形全等”是真命题吗?
定理应用
如图, 在ΔABC中, D是BC的中点, DE⊥ AB于E, DF⊥AC于F, 且DE=DF, 求证:AB=AC.
A
B
C
D
E
F
定理应用
例 已知: 如图, 已知P是∠AOB内一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE, 求证:点P在∠AOB的平分线上.
由此,你能得出什么结论?
几何语言:
∵DP⊥OA,PE⊥OB,且PD=PE
∴OP平分∠AOB
角平分线性质定理的逆定理:
角的内部,到角两边距离相等的点,在这个角的平分线上。
定理应用
已知Δ ABC,用直尺和圆规作一点P ,使它到三边距离都相等(要求作出图形,并保留作图痕迹)
知识:
1、尺规作图 ——— 已知斜边和一直角边作直角三角形;
2、“斜边、直角边定理(HL)”;
3、角平分线性质的逆定理。
方法:实验——猜想——验证——推理
课堂小结
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
