3.3垂径定理及其推论(共11张PPT)浙教版数学九年级上册
文档属性
| 名称 | 3.3垂径定理及其推论(共11张PPT)浙教版数学九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 345.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-22 18:15:24 | ||
图片预览



文档简介
(共11张PPT)
垂径定理及其推论
活动一:猜一猜
2、用“如果…那么…” 的形式表述上面的命题。
AE=BE
AC=BC
⌒
⌒
AD=BD
⌒
⌒
结论:
CD是直径
CD⊥AB
条件:
1、作图:画⊙O的一条直径CD,在CD上任取一点E,过E作一条与直径CD垂直的弦AB。
问题:(1)画出的图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?
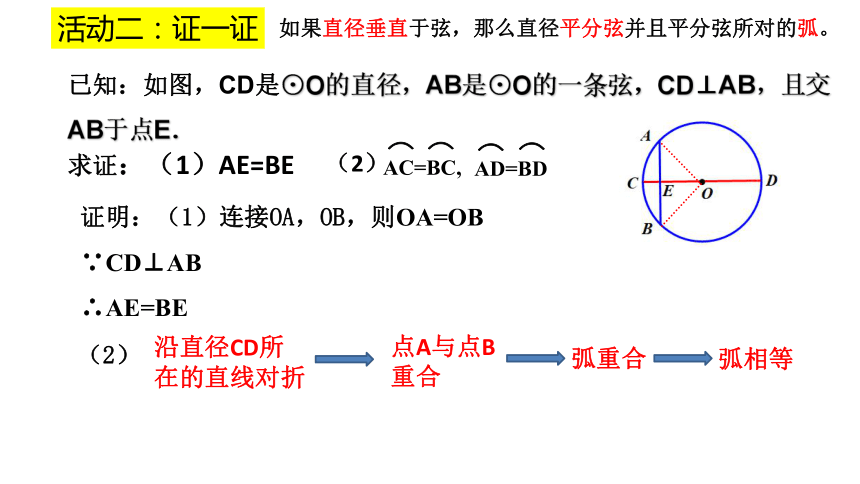
已知:如图,CD是⊙O的直径,AB是⊙O的一条弦,CD⊥AB,且交AB于点E.
求证:(1)AE=BE
活动二:证一证
如果直径垂直于弦,那么直径平分弦并且平分弦所对的弧。
AC=BC,
⌒
⌒
AD=BD
⌒
⌒
证明:(1)连接OA,OB,则OA=OB
∵CD⊥AB
∴AE=BE
(2)
弧相等
弧重合
沿直径CD所在的直线对折
点A与点B 重合
(2)
垂径定理:垂直于弦的直径平分这条弦,并且平分弦
所对的弧.
∵CD为直径,CD⊥AB
∴ EA=EB, AC=BC,AD=BD
⌒
⌒
⌒
⌒
几何语言:
活动三:理一理
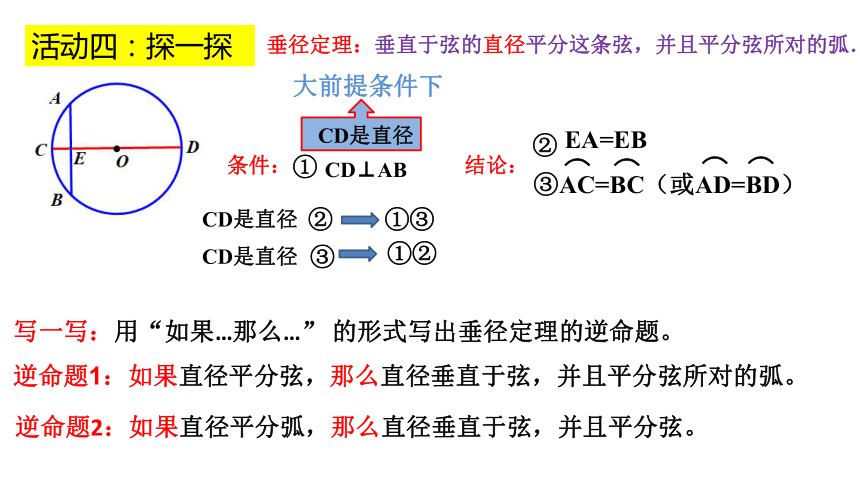
活动四:探一探
逆命题1:如果直径平分弦,那么直径垂直于弦,并且平分弦所对的弧。
逆命题2:如果直径平分弧,那么直径垂直于弦,并且平分弦。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
写一写:用“如果…那么…” 的形式写出垂径定理的逆命题。
CD是直径
CD⊥AB
条件:
结论:
EA=EB
AC=BC(或AD=BD)
⌒
⌒
⌒
⌒
②
③
①
大前提条件下
②
CD是直径
①③
CD是直径
③
①②
已知:如图,CD是⊙O的直径,AB是⊙O的一条弦, AE=BE ,且交AB
于点E。
求证:CD⊥AB ,
逆命题1:如果直径平分弦(不是直径),那么直径垂直于弦,并且平分弦所对的弧。
AC=BC,
⌒
⌒
AD=BD
⌒
⌒
逆命题1:如果直径平分弦,那么直径垂直于弦,并且平分弦所对的弧。
证明:
连接OA,OB,则OA=OB
∵AE=BE
∴ CD⊥AB
∴AC=BC, AD=BD
⌒
⌒
⌒
⌒
证明
逆命题2:如果直径平分弧,那么直径垂直平分弧所对的弦
已知:如图,CD是⊙O的直径,AB是⊙O的一条弦, 且交AB于点E.
AC=BC,
⌒
⌒
求证:CD⊥AB ,AE=BE
证明:
A,B关于直线CD对称
AC=BC
⌒
⌒
沿CD所在的直线对折AC与BC重合
⌒
⌒
点A与点B重合
CD垂直平分弦AB
证明
定理1
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的弧.
平分弧的直径,垂直平分弧所对的弦.
定理2
∵CD为直径, EA=EB
∴ CD⊥AB, AC=BC,AD=BD
几何语言:
⌒
⌒
⌒
⌒
几何语言:
∵CD为直径, AC=BC
∴ CD⊥AB, EA=EB
⌒
⌒
逆定理-得出
只要具备其中一个条件,就可推出其余两个结论.
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
定理1:平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的弧.
定理2:平分弧的直径,垂直平分弧所对的弦.
在直径(CD)的前提下
②平分弦( EA=EB )
①垂直于弦(CD⊥AB)
⌒
⌒
归纳总结
③平分弧( AC=BC,AD=BD)
⌒
⌒
如图,在⊙O中弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。
活动五:用一用
总结——升华
轴对称图形
垂径定理及其逆定理
基本策略
证一证
理一理
猜一猜
应用(下节课)
探一探
垂径定理及其推论
活动一:猜一猜
2、用“如果…那么…” 的形式表述上面的命题。
AE=BE
AC=BC
⌒
⌒
AD=BD
⌒
⌒
结论:
CD是直径
CD⊥AB
条件:
1、作图:画⊙O的一条直径CD,在CD上任取一点E,过E作一条与直径CD垂直的弦AB。
问题:(1)画出的图是轴对称图形吗?如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?
已知:如图,CD是⊙O的直径,AB是⊙O的一条弦,CD⊥AB,且交AB于点E.
求证:(1)AE=BE
活动二:证一证
如果直径垂直于弦,那么直径平分弦并且平分弦所对的弧。
AC=BC,
⌒
⌒
AD=BD
⌒
⌒
证明:(1)连接OA,OB,则OA=OB
∵CD⊥AB
∴AE=BE
(2)
弧相等
弧重合
沿直径CD所在的直线对折
点A与点B 重合
(2)
垂径定理:垂直于弦的直径平分这条弦,并且平分弦
所对的弧.
∵CD为直径,CD⊥AB
∴ EA=EB, AC=BC,AD=BD
⌒
⌒
⌒
⌒
几何语言:
活动三:理一理
活动四:探一探
逆命题1:如果直径平分弦,那么直径垂直于弦,并且平分弦所对的弧。
逆命题2:如果直径平分弧,那么直径垂直于弦,并且平分弦。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
写一写:用“如果…那么…” 的形式写出垂径定理的逆命题。
CD是直径
CD⊥AB
条件:
结论:
EA=EB
AC=BC(或AD=BD)
⌒
⌒
⌒
⌒
②
③
①
大前提条件下
②
CD是直径
①③
CD是直径
③
①②
已知:如图,CD是⊙O的直径,AB是⊙O的一条弦, AE=BE ,且交AB
于点E。
求证:CD⊥AB ,
逆命题1:如果直径平分弦(不是直径),那么直径垂直于弦,并且平分弦所对的弧。
AC=BC,
⌒
⌒
AD=BD
⌒
⌒
逆命题1:如果直径平分弦,那么直径垂直于弦,并且平分弦所对的弧。
证明:
连接OA,OB,则OA=OB
∵AE=BE
∴ CD⊥AB
∴AC=BC, AD=BD
⌒
⌒
⌒
⌒
证明
逆命题2:如果直径平分弧,那么直径垂直平分弧所对的弦
已知:如图,CD是⊙O的直径,AB是⊙O的一条弦, 且交AB于点E.
AC=BC,
⌒
⌒
求证:CD⊥AB ,AE=BE
证明:
A,B关于直线CD对称
AC=BC
⌒
⌒
沿CD所在的直线对折AC与BC重合
⌒
⌒
点A与点B重合
CD垂直平分弦AB
证明
定理1
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的弧.
平分弧的直径,垂直平分弧所对的弦.
定理2
∵CD为直径, EA=EB
∴ CD⊥AB, AC=BC,AD=BD
几何语言:
⌒
⌒
⌒
⌒
几何语言:
∵CD为直径, AC=BC
∴ CD⊥AB, EA=EB
⌒
⌒
逆定理-得出
只要具备其中一个条件,就可推出其余两个结论.
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.
定理1:平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的弧.
定理2:平分弧的直径,垂直平分弧所对的弦.
在直径(CD)的前提下
②平分弦( EA=EB )
①垂直于弦(CD⊥AB)
⌒
⌒
归纳总结
③平分弧( AC=BC,AD=BD)
⌒
⌒
如图,在⊙O中弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。
活动五:用一用
总结——升华
轴对称图形
垂径定理及其逆定理
基本策略
证一证
理一理
猜一猜
应用(下节课)
探一探
同课章节目录
