解直角三角形 整章复习
图片预览


文档简介
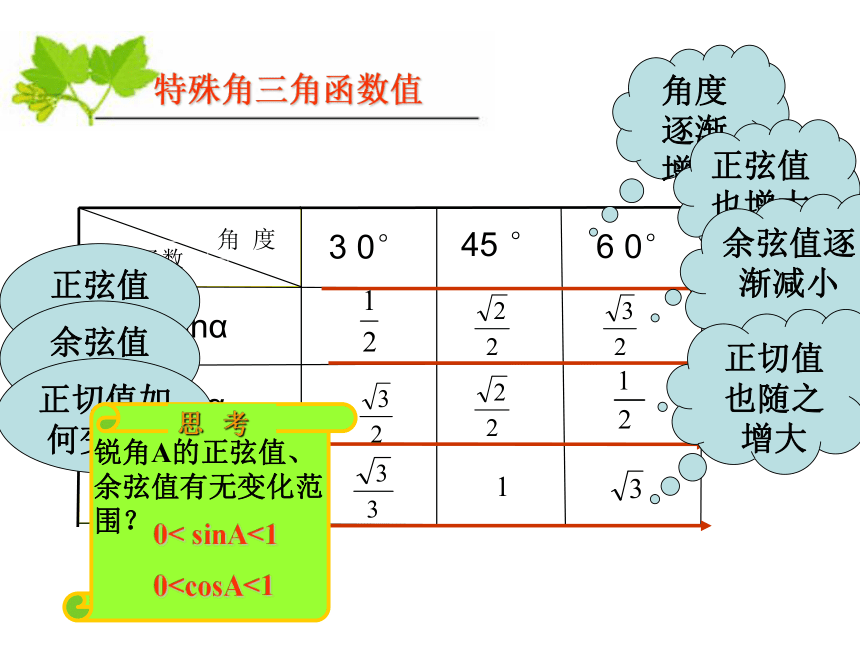
课件15张PPT。 解直角三角形复习课ABCabc你知道关于Rt△的哪些知识?说一说你从哪几方面思考?(分类讨论)⑴ 边:⑵ 角:⑶ 边角:sinA=,cosA= , tanA= ,tanαcosαsinα6 0°45 °3 0°角 度三角函数特殊角三角函数值1角度逐渐增大正弦值如何变化?正弦值也增大余弦值如何变化?余弦值逐渐减小正切值如何变化?正切值也随之增大锐角A的正弦值、余弦值有无变化范围?0< sinA<1
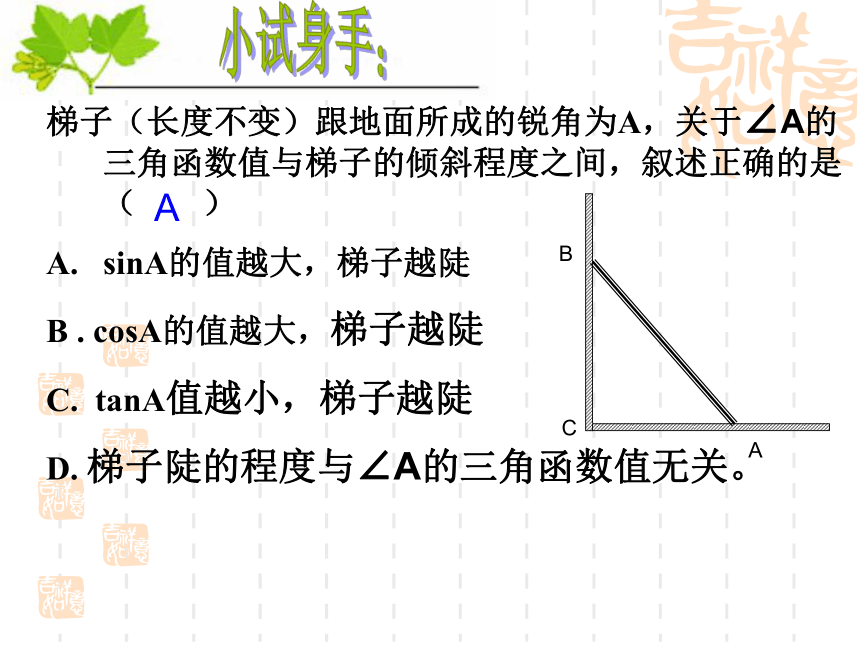
0sinA的值越大,梯子越陡
B . cosA的值越大,梯子越陡
C. tanA值越小,梯子越陡
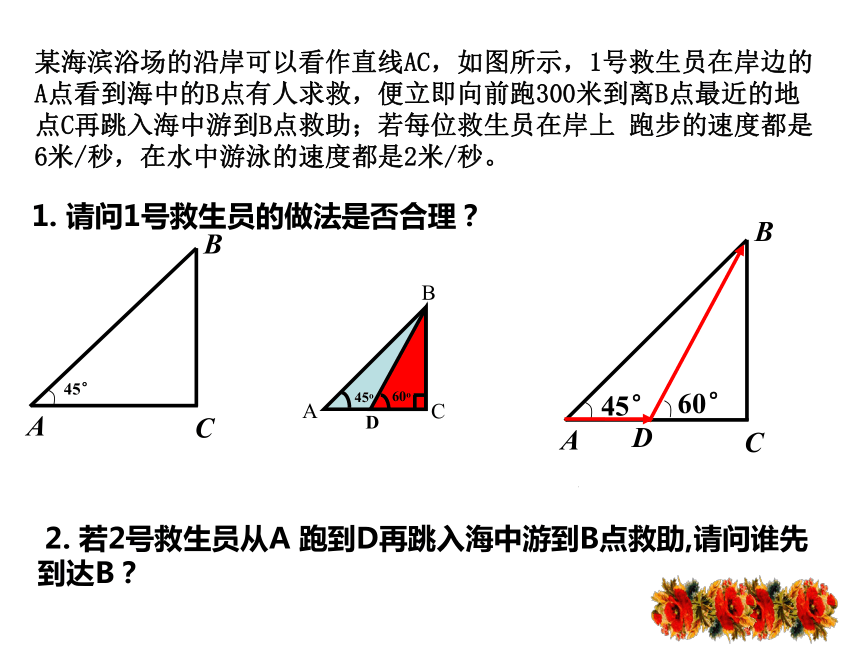
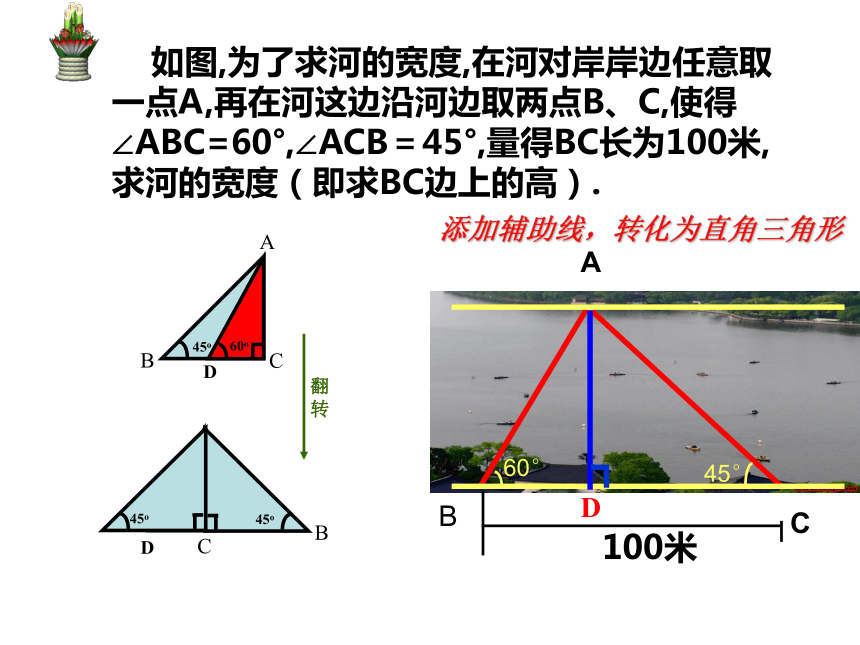
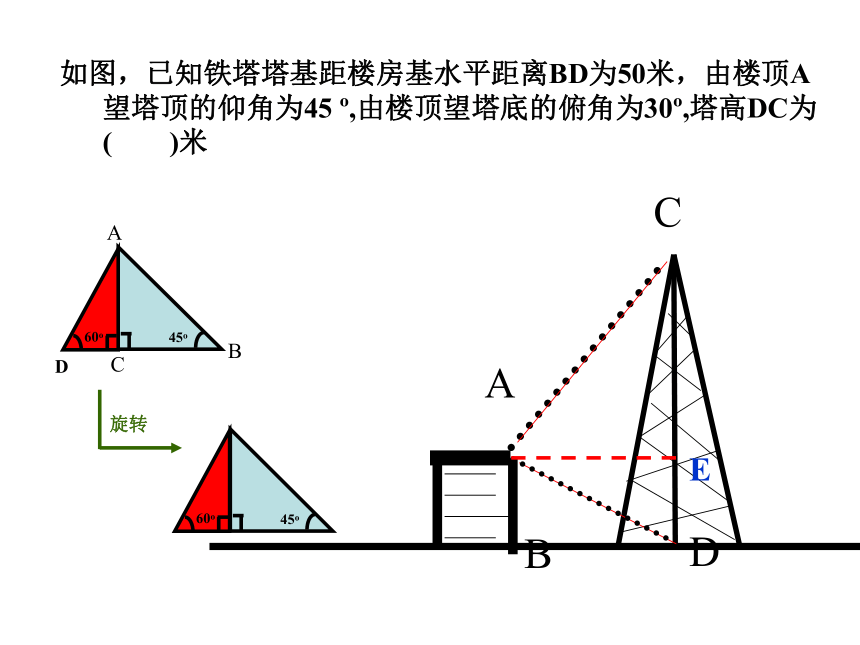
D. 梯子陡的程度与∠A的三角函数值无关。小试身手:A某海滨浴场的沿岸可以看作直线AC,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的地点C再跳入海中游到B点救助;若每位救生员在岸上 跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒。D 1. 请问1号救生员的做法是否合理? 2. 若2号救生员从A 跑到D再跳入海中游到B点救助,请问谁先到达B? 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).D60°45° 100米ABC添加辅助线,转化为直角三角形D如图,已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 o,由楼顶望塔底的俯角为30o,塔高DC为 ( )米
C E
D问题1楼房AB的高度是多少?问题2楼房CD的高度是多少?
45o简单回顾知一边一锐角解直角三角形知两边解直角三角形非直角三角形:添设辅助线转化为
解直角三角形解直角三角形三角形解直角两种基本图形在码头A的北偏东60°方向有一个海岛,离该岛中心P点的15海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B点,这时岛中心P在北偏东45°方向,
船有无触礁的危险(1)若货船不改变航向,你认为货船会有触礁的危险吗?PABH600450暗礁区问题1:要判断货轮是否有触礁危险,关键是要解决怎样的一个数学问题? PAB600450暗礁区(2)为了避开暗礁区,船必须改变航向,问船至少转过多少的角度,才能避开暗礁区?E问题2:船恰好避开暗礁区,此时船的航线与暗礁区有怎样的位置关系?船有无触礁的危险H现实问题 数学模型 实际问题的解 数学问题的解 逻辑推理 实际问题的解题思路台风是一种自然灾害,它以台风中心为圆心在周围10千米范围形成气旋风暴,有极强的破坏力.如图,据气象观测,距沿海某城市A的正南方向220千米B 处有一台风中心,其中心最大风力为12级,每远离中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.BAC(1)该城市是否会受到这次台风的影响?请说明理由.(2)若受到台风影响,那么台风影响该城市的持续时间有多长? (3)该城市受到台风影响的最大风力为几级?会受台风影响吗?DEF1、直角三角形与非直角三角形的基本解题思路;小结:
0
B . cosA的值越大,梯子越陡
C. tanA值越小,梯子越陡
D. 梯子陡的程度与∠A的三角函数值无关。小试身手:A某海滨浴场的沿岸可以看作直线AC,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的地点C再跳入海中游到B点救助;若每位救生员在岸上 跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒。D 1. 请问1号救生员的做法是否合理? 2. 若2号救生员从A 跑到D再跳入海中游到B点救助,请问谁先到达B? 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高).D60°45° 100米ABC添加辅助线,转化为直角三角形D如图,已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 o,由楼顶望塔底的俯角为30o,塔高DC为 ( )米
C E
D问题1楼房AB的高度是多少?问题2楼房CD的高度是多少?
45o简单回顾知一边一锐角解直角三角形知两边解直角三角形非直角三角形:添设辅助线转化为
解直角三角形解直角三角形三角形解直角两种基本图形在码头A的北偏东60°方向有一个海岛,离该岛中心P点的15海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B点,这时岛中心P在北偏东45°方向,
船有无触礁的危险(1)若货船不改变航向,你认为货船会有触礁的危险吗?PABH600450暗礁区问题1:要判断货轮是否有触礁危险,关键是要解决怎样的一个数学问题? PAB600450暗礁区(2)为了避开暗礁区,船必须改变航向,问船至少转过多少的角度,才能避开暗礁区?E问题2:船恰好避开暗礁区,此时船的航线与暗礁区有怎样的位置关系?船有无触礁的危险H现实问题 数学模型 实际问题的解 数学问题的解 逻辑推理 实际问题的解题思路台风是一种自然灾害,它以台风中心为圆心在周围10千米范围形成气旋风暴,有极强的破坏力.如图,据气象观测,距沿海某城市A的正南方向220千米B 处有一台风中心,其中心最大风力为12级,每远离中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响.BAC(1)该城市是否会受到这次台风的影响?请说明理由.(2)若受到台风影响,那么台风影响该城市的持续时间有多长? (3)该城市受到台风影响的最大风力为几级?会受台风影响吗?DEF1、直角三角形与非直角三角形的基本解题思路;小结:
