相似三角形复习课
图片预览





文档简介
课件26张PPT。相似三角形复习课〖知识点〗1.相似三角形的定义。
2.相似三角形的判定。
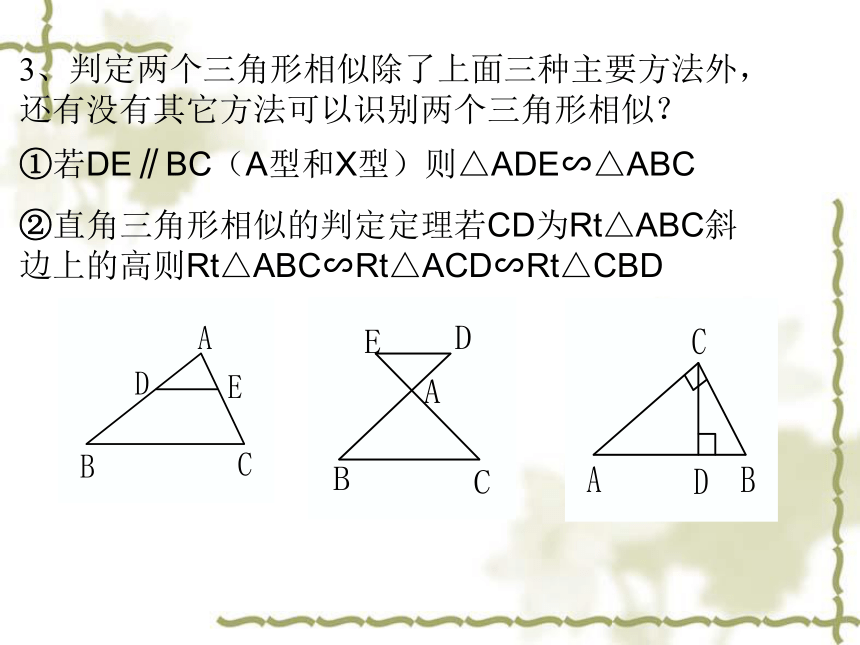
3.相似三角形的性质的应用。〖复习〗1、相似三角形的定义是什么?答:三边对应成成比例,三个角对应相等的两个三角形叫做相似三角形 。2、判定两个三角形相似有哪些主要方法?答:①两角对应相等,两个三角形相似.②两条边对应成比例且夹角相等,两三角形相似.③三边对应成比例,那么这两个三角形相似. ②直角三角形相似的判定定理若CD为Rt△ABC斜边上的高则Rt△ABC∽Rt△ACD∽Rt△CBD①若DE∥BC(A型和X型)则△ADE∽△ABC3、判定两个三角形相似除了上面三种主要方法外,还有没有其它方法可以识别两个三角形相似?4、相似三角形有哪些性质答: 1、对应角相等,对应边 ,
2、相似三角形的对应边的比叫做________,一般用k表示.
3、对应角平分线、对应中线、对应高线、对应周长的比都等于 。
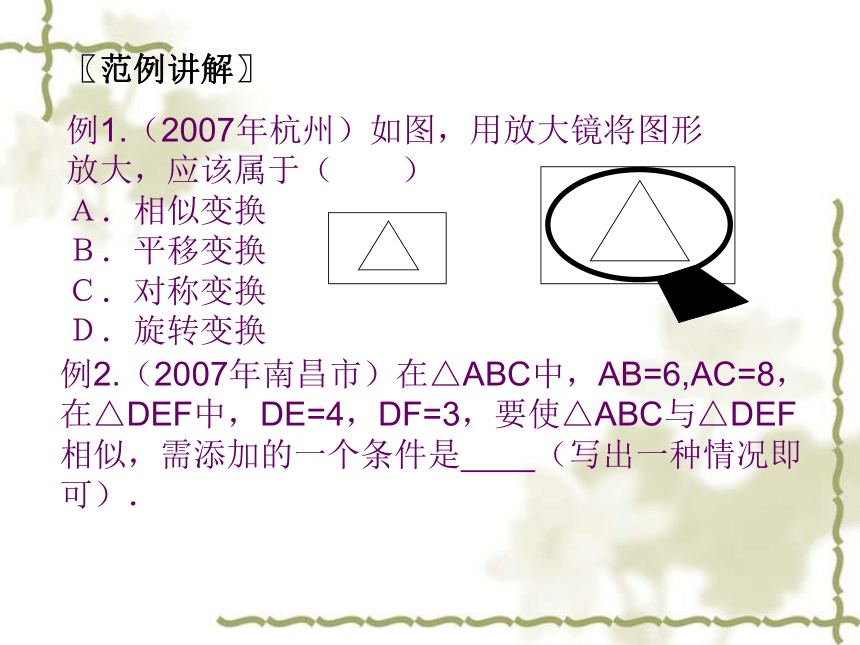
4、相似三角形面积的比等于 。例2.(2007年南昌市)在△ABC中,AB=6,AC=8,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,需添加的一个条件是 (写出一种情况即可).例1.(2007年杭州)如图,用放大镜将图形放大,应该属于( )
A.相似变换
B.平移变换
C.对称变换
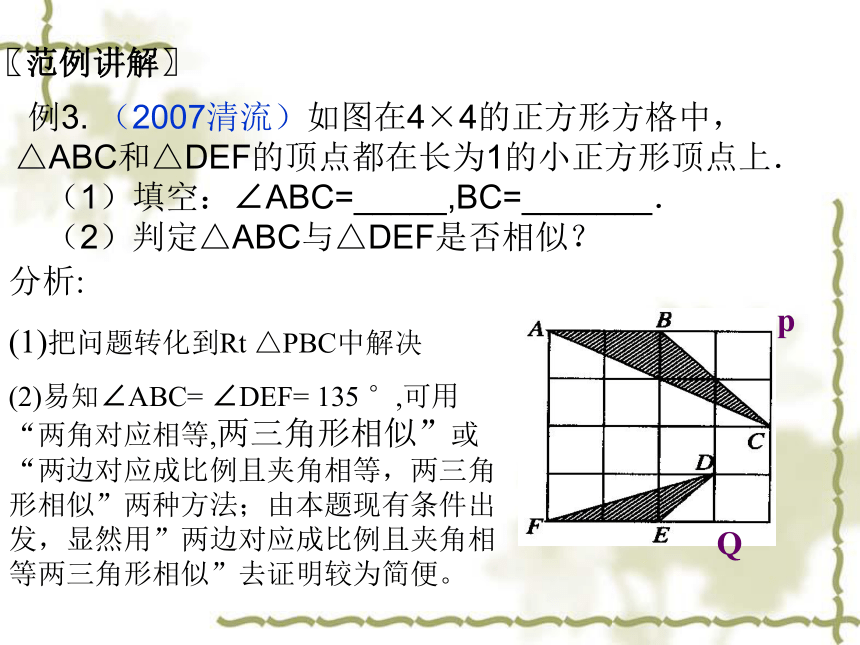
D.旋转变换〖范例讲解〗例3. (2007清流)如图在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.
(1)填空:∠ABC=_____,BC=_______.
(2)判定△ABC与△DEF是否相似?〖范例讲解〗分析:
(1)把问题转化到Rt △PBC中解决
(2)易知∠ABC= ∠DEF= 135 °,可用“两角对应相等,两三角形相似”或“两边对应成比例且夹角相等,两三角形相似”两种方法;由本题现有条件出发,显然用”两边对应成比例且夹角相等两三角形相似”去证明较为简便。
pQ例3.如图在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.
(1)填空:∠ABC=_____,BC=_______.
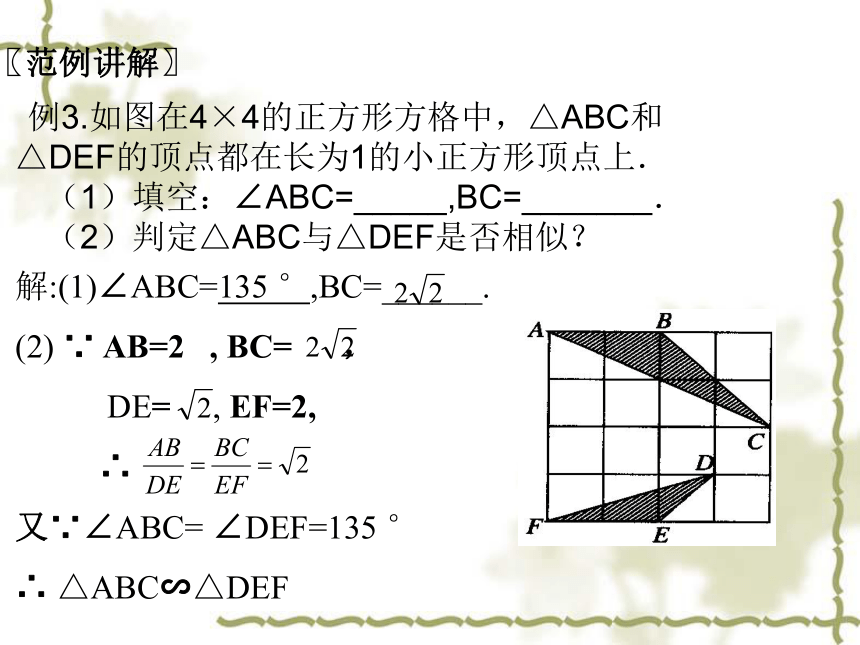
(2)判定△ABC与△DEF是否相似?〖范例讲解〗解:(1)∠ABC=135 °,BC=______.
(2) ∵ AB=2 , BC= ,
DE= , EF=2,
∴
又∵∠ABC= ∠DEF=135 °
∴ △ABC∽△DEF①所有的等腰三角形都相似.②所有的直角三角形都相似.③所有的等边三角形都相似.④所有的等腰直角三角形都相似.(×)(√)(√)(×)1.判断题:〖巩固训练〗2. (1)两个相似三角形相似比等于3:2,则对应边上的高的比为______,周长之比为________,面积之比为_________. (2)2007年盐城市)某一时刻,身高为165cm的小芳影长为55cm,此时,小玲在同一地点测得旗杆的影长为5m,则该旗杆的高度为 m.3:23:29:43.(2007年青岛)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度
应为 cm.
4.如图所示,当满足下列条件之一时,都可判定△ADC∽△ACB.
① ,
② ,
③ 。
∠ACD=∠B∠ACB=∠ADC 解 :∵D、E分别为AB、AC的中点
∴DE∥BC,且
∴ △ADE∽△ABC
∴ △ADE与△ABC的相似比为1:2
5. △ ABC中,AB的中点为D,AC的中点为E,连结DE, 求△ ADE与△ ABC的相似比。 解: ∵DE∥BC
∴△ADE∽△ABC
∵AD:DB=2:3
∴AD:AB=2:5
即△ADE与△ABC的相似比为2:5
∴ △ADE与△ABC的面积比为4:256.如图,DE∥BC, AD:DB=2:3, 求△ AED
和△ ABC 的面积比. 解:∵∠AED=∠B, ∠A=∠A
∴△AED∽ △ABC(两角对
应相等,两三角形相似)
∴
∴ AD·BC=AC·DE7. △ ABC中,D、E分别是AB、AC上的点,
且∠AED= ∠ B,求证:AD·BC=AC·DE 8.(2007年怀化市)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距BD=15m,,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.ABCDEF〖拓展延伸〗
1.D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB由已知两个三角形有二个角对应相等,所以两三角形相似,本题可证。要证明AC2=AD·AB,需要先将乘积式改写为比例式 ,再证明AC、AD、AB所在的两个三角形相似。分析:〖拓展延伸〗
1.D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB证明:∵ ∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·AB〖拓展延伸〗
2.(2007年佛山市)在Rt△ABC中,∠BAC=90°,AB=AC=2,,点在所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).
如图1,若点在线段上运动,交于E.
①求证:△ABD∽△DCE;
②当△ADE是等腰三角形时,求AE的长.3.(2007年十堰)如图所示,点O是△ABC外的一点,分别在射线OA、OB、OC上取一点A’、B’、C’,
使得 ,连结A’B’、B’C’、C’A’,所得
△A’B’C’与△ABC是否相似?证明你的结论。〖拓展延伸〗4.已知,如图,在△ABC中,D为BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F,求证:△ABC∽△FCD; 证明:因为AD=AC
∴∠ADC=∠ACD
因为D为BC的中点,DE⊥BC
∴EB=EC
∴∠B=∠ECB
∴△ABC∽△FCD〖拓展延伸〗5.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似16.如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC边于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式.〖学习小结〗1.相似三角形的定义。
2.相似三角形的判定。
3.相似三角形的性质的应用。〖课外作业〗课本P80复习题第4、5、6、7、9、12、14、19、20题.
2.相似三角形的判定。
3.相似三角形的性质的应用。〖复习〗1、相似三角形的定义是什么?答:三边对应成成比例,三个角对应相等的两个三角形叫做相似三角形 。2、判定两个三角形相似有哪些主要方法?答:①两角对应相等,两个三角形相似.②两条边对应成比例且夹角相等,两三角形相似.③三边对应成比例,那么这两个三角形相似. ②直角三角形相似的判定定理若CD为Rt△ABC斜边上的高则Rt△ABC∽Rt△ACD∽Rt△CBD①若DE∥BC(A型和X型)则△ADE∽△ABC3、判定两个三角形相似除了上面三种主要方法外,还有没有其它方法可以识别两个三角形相似?4、相似三角形有哪些性质答: 1、对应角相等,对应边 ,
2、相似三角形的对应边的比叫做________,一般用k表示.
3、对应角平分线、对应中线、对应高线、对应周长的比都等于 。
4、相似三角形面积的比等于 。例2.(2007年南昌市)在△ABC中,AB=6,AC=8,在△DEF中,DE=4,DF=3,要使△ABC与△DEF相似,需添加的一个条件是 (写出一种情况即可).例1.(2007年杭州)如图,用放大镜将图形放大,应该属于( )
A.相似变换
B.平移变换
C.对称变换
D.旋转变换〖范例讲解〗例3. (2007清流)如图在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.
(1)填空:∠ABC=_____,BC=_______.
(2)判定△ABC与△DEF是否相似?〖范例讲解〗分析:
(1)把问题转化到Rt △PBC中解决
(2)易知∠ABC= ∠DEF= 135 °,可用“两角对应相等,两三角形相似”或“两边对应成比例且夹角相等,两三角形相似”两种方法;由本题现有条件出发,显然用”两边对应成比例且夹角相等两三角形相似”去证明较为简便。
pQ例3.如图在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.
(1)填空:∠ABC=_____,BC=_______.
(2)判定△ABC与△DEF是否相似?〖范例讲解〗解:(1)∠ABC=135 °,BC=______.
(2) ∵ AB=2 , BC= ,
DE= , EF=2,
∴
又∵∠ABC= ∠DEF=135 °
∴ △ABC∽△DEF①所有的等腰三角形都相似.②所有的直角三角形都相似.③所有的等边三角形都相似.④所有的等腰直角三角形都相似.(×)(√)(√)(×)1.判断题:〖巩固训练〗2. (1)两个相似三角形相似比等于3:2,则对应边上的高的比为______,周长之比为________,面积之比为_________. (2)2007年盐城市)某一时刻,身高为165cm的小芳影长为55cm,此时,小玲在同一地点测得旗杆的影长为5m,则该旗杆的高度为 m.3:23:29:43.(2007年青岛)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体AB的高度为36cm,那么它在暗盒中所成的像CD的高度
应为 cm.
4.如图所示,当满足下列条件之一时,都可判定△ADC∽△ACB.
① ,
② ,
③ 。
∠ACD=∠B∠ACB=∠ADC 解 :∵D、E分别为AB、AC的中点
∴DE∥BC,且
∴ △ADE∽△ABC
∴ △ADE与△ABC的相似比为1:2
5. △ ABC中,AB的中点为D,AC的中点为E,连结DE, 求△ ADE与△ ABC的相似比。 解: ∵DE∥BC
∴△ADE∽△ABC
∵AD:DB=2:3
∴AD:AB=2:5
即△ADE与△ABC的相似比为2:5
∴ △ADE与△ABC的面积比为4:256.如图,DE∥BC, AD:DB=2:3, 求△ AED
和△ ABC 的面积比. 解:∵∠AED=∠B, ∠A=∠A
∴△AED∽ △ABC(两角对
应相等,两三角形相似)
∴
∴ AD·BC=AC·DE7. △ ABC中,D、E分别是AB、AC上的点,
且∠AED= ∠ B,求证:AD·BC=AC·DE 8.(2007年怀化市)九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距BD=15m,,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.ABCDEF〖拓展延伸〗
1.D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB由已知两个三角形有二个角对应相等,所以两三角形相似,本题可证。要证明AC2=AD·AB,需要先将乘积式改写为比例式 ,再证明AC、AD、AB所在的两个三角形相似。分析:〖拓展延伸〗
1.D为△ABC中AB边上一点,∠ACD= ∠ ABC.
求证:AC2=AD·AB证明:∵ ∠ACD= ∠ ABC
∠A = ∠ A
∴ △ABC △ACD
∴
∴ AC2=AD·AB〖拓展延伸〗
2.(2007年佛山市)在Rt△ABC中,∠BAC=90°,AB=AC=2,,点在所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).
如图1,若点在线段上运动,交于E.
①求证:△ABD∽△DCE;
②当△ADE是等腰三角形时,求AE的长.3.(2007年十堰)如图所示,点O是△ABC外的一点,分别在射线OA、OB、OC上取一点A’、B’、C’,
使得 ,连结A’B’、B’C’、C’A’,所得
△A’B’C’与△ABC是否相似?证明你的结论。〖拓展延伸〗4.已知,如图,在△ABC中,D为BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F,求证:△ABC∽△FCD; 证明:因为AD=AC
∴∠ADC=∠ACD
因为D为BC的中点,DE⊥BC
∴EB=EC
∴∠B=∠ECB
∴△ABC∽△FCD〖拓展延伸〗5.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似16.如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC边于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式.〖学习小结〗1.相似三角形的定义。
2.相似三角形的判定。
3.相似三角形的性质的应用。〖课外作业〗课本P80复习题第4、5、6、7、9、12、14、19、20题.
同课章节目录
