圆的期末复习
图片预览

文档简介
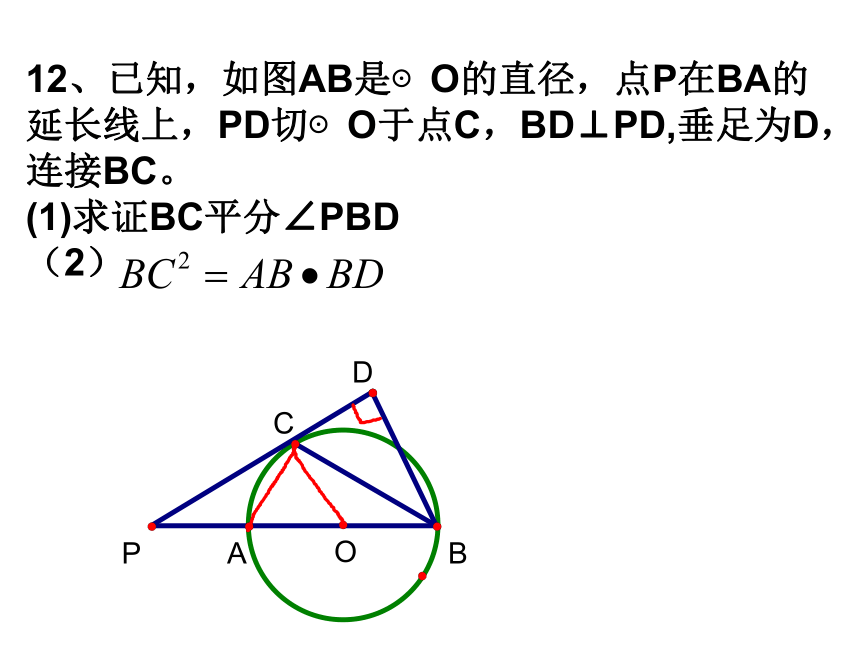
课件15张PPT。 1.已知:如图⊙O的半径为4cm,OA⊥OB,
OC⊥AB于C,OB=4 cm,OA=2 cm,
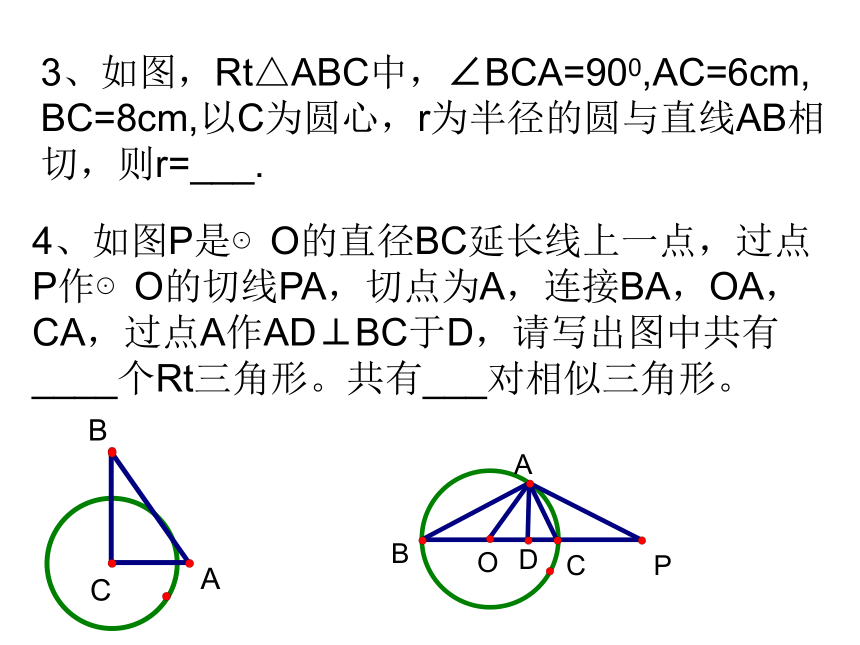
求证:AB与⊙O相切。 3、如图,Rt△ABC中,∠BCA=900,AC=6cm,
BC=8cm,以C为圆心,r为半径的圆与直线AB相
切,则r=___.4、如图P是⊙O的直径BC延长线上一点,过点
P作⊙O的切线PA,切点为A,连接BA,OA,
CA,过点A作AD⊥BC于D,请写出图中共有
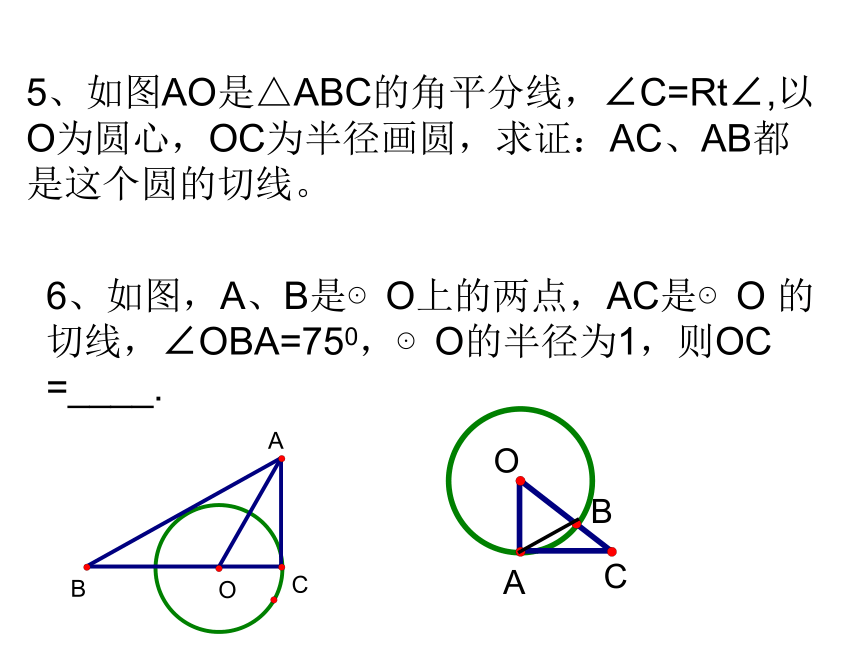
____个Rt三角形。共有___对相似三角形。5、如图AO是△ABC的角平分线,∠C=Rt∠,以
O为圆心,OC为半径画圆,求证:AC、AB都
是这个圆的切线。6、如图,A、B是⊙O上的两点,AC是⊙O 的
切线,∠OBA=750,⊙O的半径为1,则OC
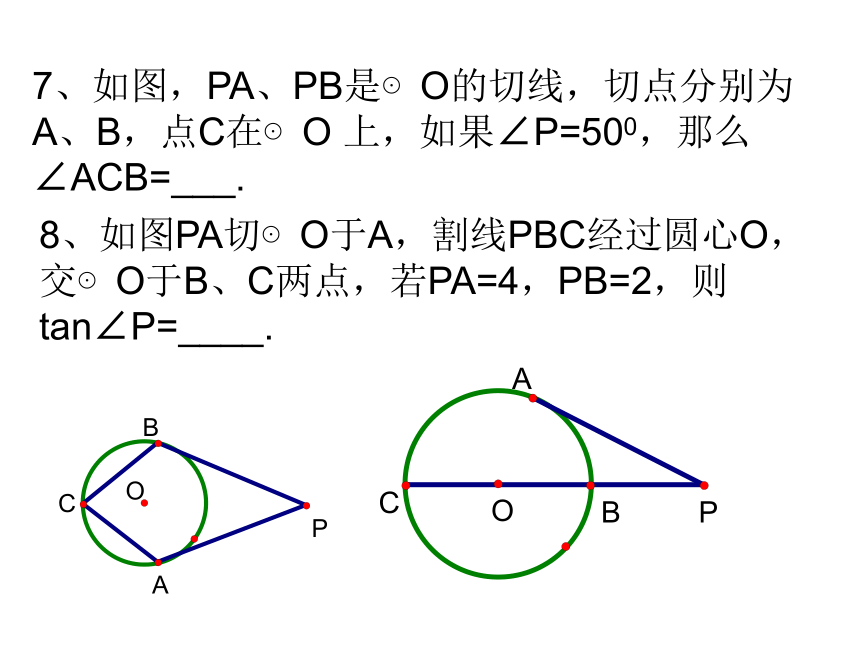
=____.7、如图,PA、PB是⊙O的切线,切点分别为
A、B,点C在⊙O 上,如果∠P=500,那么
∠ACB=___.8、如图PA切⊙O于A,割线PBC经过圆心O,
交⊙O于B、C两点,若PA=4,PB=2,则
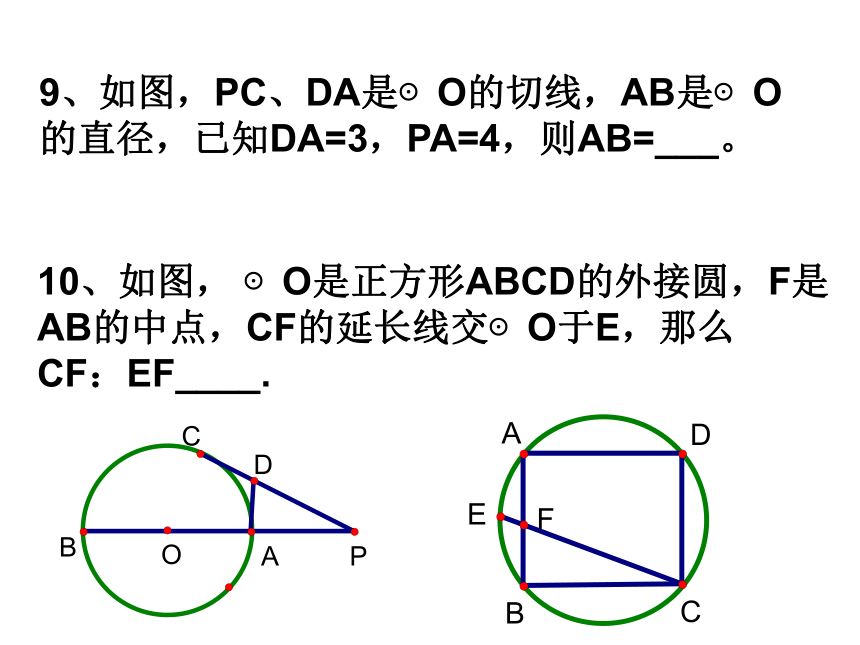
tan∠P=____.9、如图,PC、DA是⊙O的切线,AB是⊙O
的直径,已知DA=3,PA=4,则AB=___。10、如图, ⊙O是正方形ABCD的外接圆,F是
AB的中点,CF的延长线交⊙O于E,那么
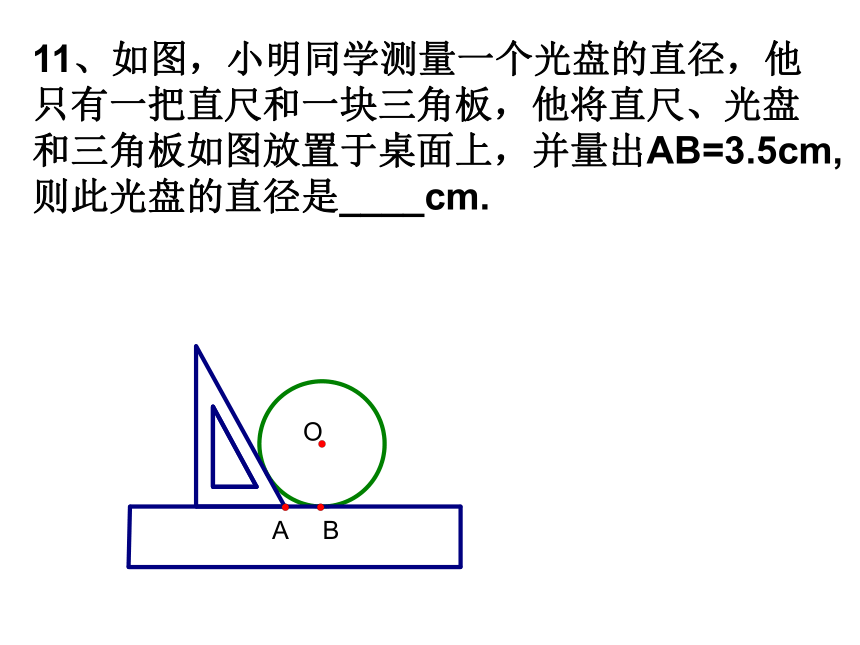
CF:EF____.11、如图,小明同学测量一个光盘的直径,他
只有一把直尺和一块三角板,他将直尺、光盘
和三角板如图放置于桌面上,并量出AB=3.5cm,
则此光盘的直径是____cm.13、如图以Rt△ABC的直角边AC为直径作⊙O,
交斜边AB于D,E是BC中点。
(1)求证:ED是⊙O的切线。
(2)如果AD=4,BD=2,求DE的长。
(3)求证:S△CBD:S△ABC=1:3。14、如图在△ABC中,∠ABC=90度,O是AB上
一点,以O为圆心,OB为半径的圆与AB交于点
E,与AC切于点D,连接DB、DE、OC。
①从图中找出一对相似三角形,并加以证明。
②若AD=2,AE=1,求CD的长。 15.如图,两个同心圆中,△ABC内接于⊙O,∠B=∠C,小圆与AB相切,
求证:AC为小圆的切线。 ????????????????????? 16.如图,已知:在△ABC中,AB=AC,以AB为直径作⊙O交BC于D,DE⊥AC于E, 求证:DE是⊙O的切线。 ?????????????????????? 17.如图,BC为⊙O 直径,△ABC内接于⊙O,P、B、C在一直线上,且PA2=PB·PC, 求证:PA是⊙O的切线。 19.已知:如图,在△ABC中,∠C=90°,BE是角平 分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆。 (1)求证AC是⊙O的切线; (2)若AD=6,AE=6 ,求DE的长。CAEDOB20.如图,以Rt△ABC的斜边AB为直径作⊙O,G为⊙O上一点,过点G作AB的垂线,分别交AB、AC和BC的延长线于D、E、F,求证:DG2 = DE · DFACDBFEGO●分析:∵ DG 2 = AD · BD∴只需证: DE · DF = AD · BD将上式化为比例式:∴ 只需证: △ADE∽△FDB┓┏问题得证。21.如图,⊙O的直径AB=4,与半圆内切的动圆O1与AB切于点M,设⊙ O1半径为y,AM长为x,求y关于x的函数关系式.Px2-xy2-y22.如图,在矩形ABCD中,AB=20cm,BC=4cm,点⊙p从A开始折线A—B—C—D以4cm/秒的速度移动,点⊙Q从C开始沿CD边以1cm/秒的速度移动,如果点⊙P, ⊙Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒) 如果⊙P和⊙Q的半径都是2cm,那么t为何值时, ⊙P和⊙Q外切?ABCD
OC⊥AB于C,OB=4 cm,OA=2 cm,
求证:AB与⊙O相切。 3、如图,Rt△ABC中,∠BCA=900,AC=6cm,
BC=8cm,以C为圆心,r为半径的圆与直线AB相
切,则r=___.4、如图P是⊙O的直径BC延长线上一点,过点
P作⊙O的切线PA,切点为A,连接BA,OA,
CA,过点A作AD⊥BC于D,请写出图中共有
____个Rt三角形。共有___对相似三角形。5、如图AO是△ABC的角平分线,∠C=Rt∠,以
O为圆心,OC为半径画圆,求证:AC、AB都
是这个圆的切线。6、如图,A、B是⊙O上的两点,AC是⊙O 的
切线,∠OBA=750,⊙O的半径为1,则OC
=____.7、如图,PA、PB是⊙O的切线,切点分别为
A、B,点C在⊙O 上,如果∠P=500,那么
∠ACB=___.8、如图PA切⊙O于A,割线PBC经过圆心O,
交⊙O于B、C两点,若PA=4,PB=2,则
tan∠P=____.9、如图,PC、DA是⊙O的切线,AB是⊙O
的直径,已知DA=3,PA=4,则AB=___。10、如图, ⊙O是正方形ABCD的外接圆,F是
AB的中点,CF的延长线交⊙O于E,那么
CF:EF____.11、如图,小明同学测量一个光盘的直径,他
只有一把直尺和一块三角板,他将直尺、光盘
和三角板如图放置于桌面上,并量出AB=3.5cm,
则此光盘的直径是____cm.13、如图以Rt△ABC的直角边AC为直径作⊙O,
交斜边AB于D,E是BC中点。
(1)求证:ED是⊙O的切线。
(2)如果AD=4,BD=2,求DE的长。
(3)求证:S△CBD:S△ABC=1:3。14、如图在△ABC中,∠ABC=90度,O是AB上
一点,以O为圆心,OB为半径的圆与AB交于点
E,与AC切于点D,连接DB、DE、OC。
①从图中找出一对相似三角形,并加以证明。
②若AD=2,AE=1,求CD的长。 15.如图,两个同心圆中,△ABC内接于⊙O,∠B=∠C,小圆与AB相切,
求证:AC为小圆的切线。 ????????????????????? 16.如图,已知:在△ABC中,AB=AC,以AB为直径作⊙O交BC于D,DE⊥AC于E, 求证:DE是⊙O的切线。 ?????????????????????? 17.如图,BC为⊙O 直径,△ABC内接于⊙O,P、B、C在一直线上,且PA2=PB·PC, 求证:PA是⊙O的切线。 19.已知:如图,在△ABC中,∠C=90°,BE是角平 分线,DE⊥BE交AB于D,⊙O是△BDE的外接圆。 (1)求证AC是⊙O的切线; (2)若AD=6,AE=6 ,求DE的长。CAEDOB20.如图,以Rt△ABC的斜边AB为直径作⊙O,G为⊙O上一点,过点G作AB的垂线,分别交AB、AC和BC的延长线于D、E、F,求证:DG2 = DE · DFACDBFEGO●分析:∵ DG 2 = AD · BD∴只需证: DE · DF = AD · BD将上式化为比例式:∴ 只需证: △ADE∽△FDB┓┏问题得证。21.如图,⊙O的直径AB=4,与半圆内切的动圆O1与AB切于点M,设⊙ O1半径为y,AM长为x,求y关于x的函数关系式.Px2-xy2-y22.如图,在矩形ABCD中,AB=20cm,BC=4cm,点⊙p从A开始折线A—B—C—D以4cm/秒的速度移动,点⊙Q从C开始沿CD边以1cm/秒的速度移动,如果点⊙P, ⊙Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒) 如果⊙P和⊙Q的半径都是2cm,那么t为何值时, ⊙P和⊙Q外切?ABCD
