4.5 三角形的中位线 同步分层作业(含解析)
文档属性
| 名称 | 4.5 三角形的中位线 同步分层作业(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-29 17:49:17 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.5 三角形的中位线 同步分层作业
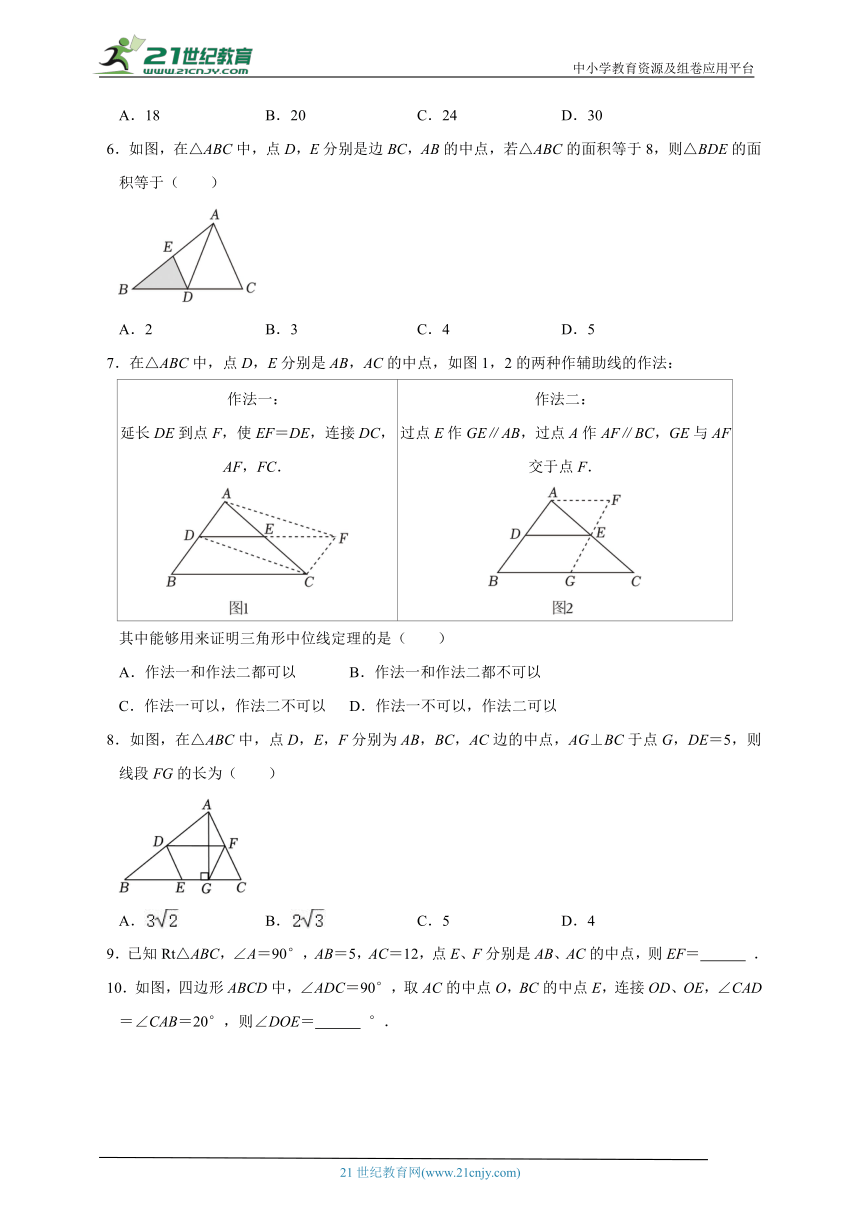
1.如图,在△ABC中,AC=BC,DE为△ABC的中位线,连接CD.若∠B=68°,则∠EDC的度数为( )
A.20° B.22° C.32° D.34°
2.如图,在△ABC中,AB=AC=3,AE⊥BC,垂足为点E,D是AC上一点,连接BD,F是BD的中点,当EF=1时,AD的长为( )
A. B.2 C.1 D.
3.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为( )
A.6.5cm B.34cm C.26cm D.52cm
4.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.3 B.2 C. D.4
5.如图,△DEF的三个顶点D,E,F分别为△ABC三边AB,AC,BC的中点,若△DEF的面积S△DEF=6,则△ABC的面积为( )
A.18 B.20 C.24 D.30
6.如图,在△ABC中,点D,E分别是边BC,AB的中点,若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
7.在△ABC中,点D,E分别是AB,AC的中点,如图1,2的两种作辅助线的作法:
作法一:延长DE到点F,使EF=DE,连接DC,AF,FC. 作法二:过点E作GE∥AB,过点A作AF∥BC,GE与AF交于点F.
其中能够用来证明三角形中位线定理的是( )
A.作法一和作法二都可以 B.作法一和作法二都不可以
C.作法一可以,作法二不可以 D.作法一不可以,作法二可以
8.如图,在△ABC中,点D,E,F分别为AB,BC,AC边的中点,AG⊥BC于点G,DE=5,则线段FG的长为( )
A. B. C.5 D.4
9.已知Rt△ABC,∠A=90°,AB=5,AC=12,点E、F分别是AB、AC的中点,则EF= .
10.如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= °.
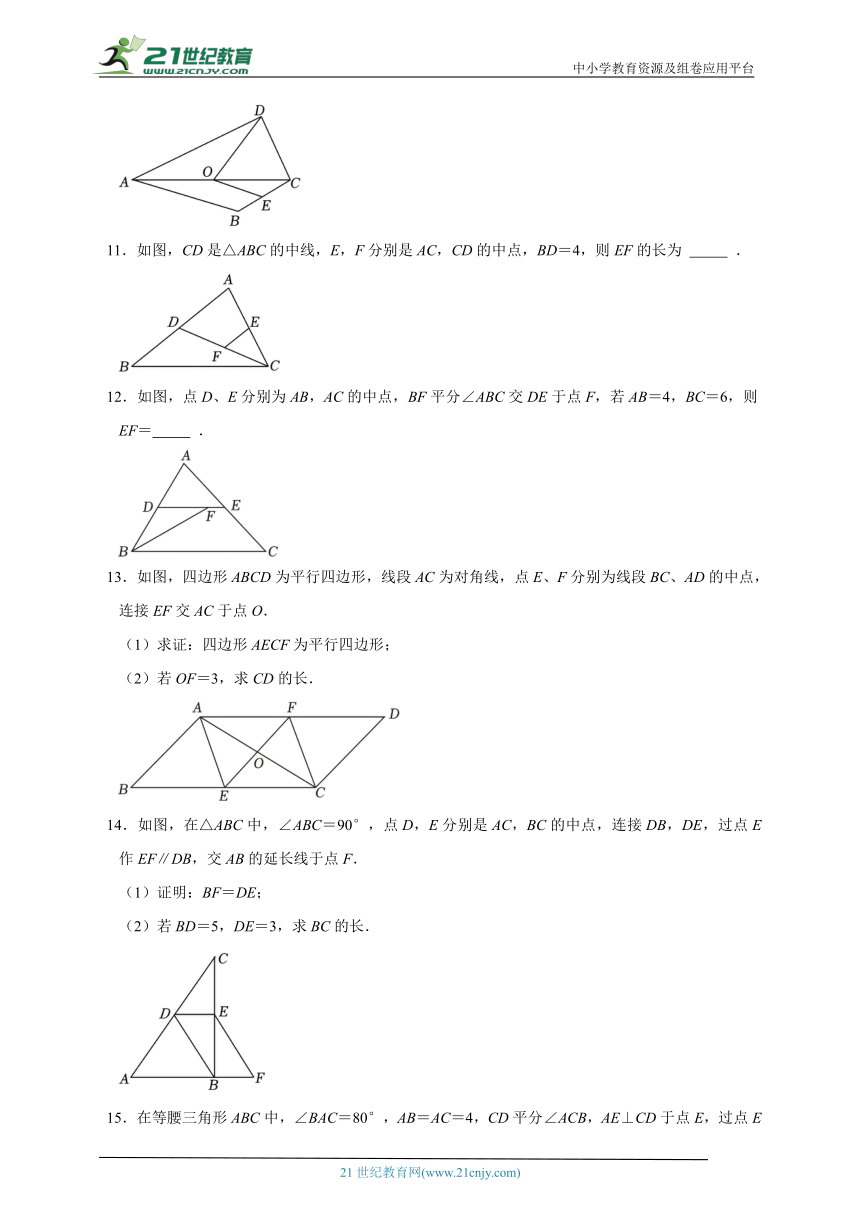
11.如图,CD是△ABC的中线,E,F分别是AC,CD的中点,BD=4,则EF的长为 .
12.如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= .
13.如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
14.如图,在△ABC中,∠ABC=90°,点D,E分别是AC,BC的中点,连接DB,DE,过点E作EF∥DB,交AB的延长线于点F.
(1)证明:BF=DE;
(2)若BD=5,DE=3,求BC的长.
15.在等腰三角形ABC中,∠BAC=80°,AB=AC=4,CD平分∠ACB,AE⊥CD于点E,过点E作EF∥BC交AC于点F.
(1)求∠AEF的度数;
(2)若G是BC的中点,连接FG,求FG的长.
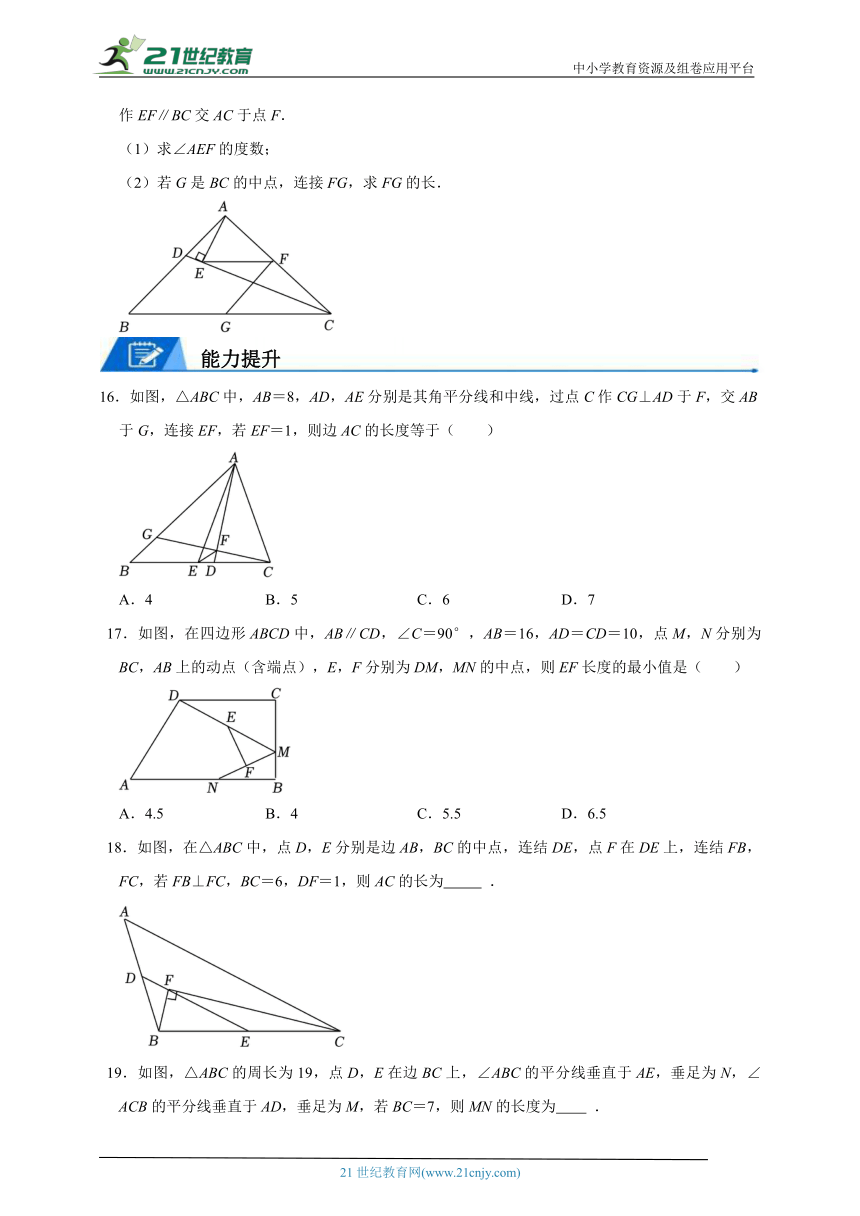
16.如图,△ABC中,AB=8,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,若EF=1,则边AC的长度等于( )
A.4 B.5 C.6 D.7
17.如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=16,AD=CD=10,点M,N分别为BC,AB上的动点(含端点),E,F分别为DM,MN的中点,则EF长度的最小值是( )
A.4.5 B.4 C.5.5 D.6.5
18.如图,在△ABC中,点D,E分别是边AB,BC的中点,连结DE,点F在DE上,连结FB,FC,若FB⊥FC,BC=6,DF=1,则AC的长为 .
19.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
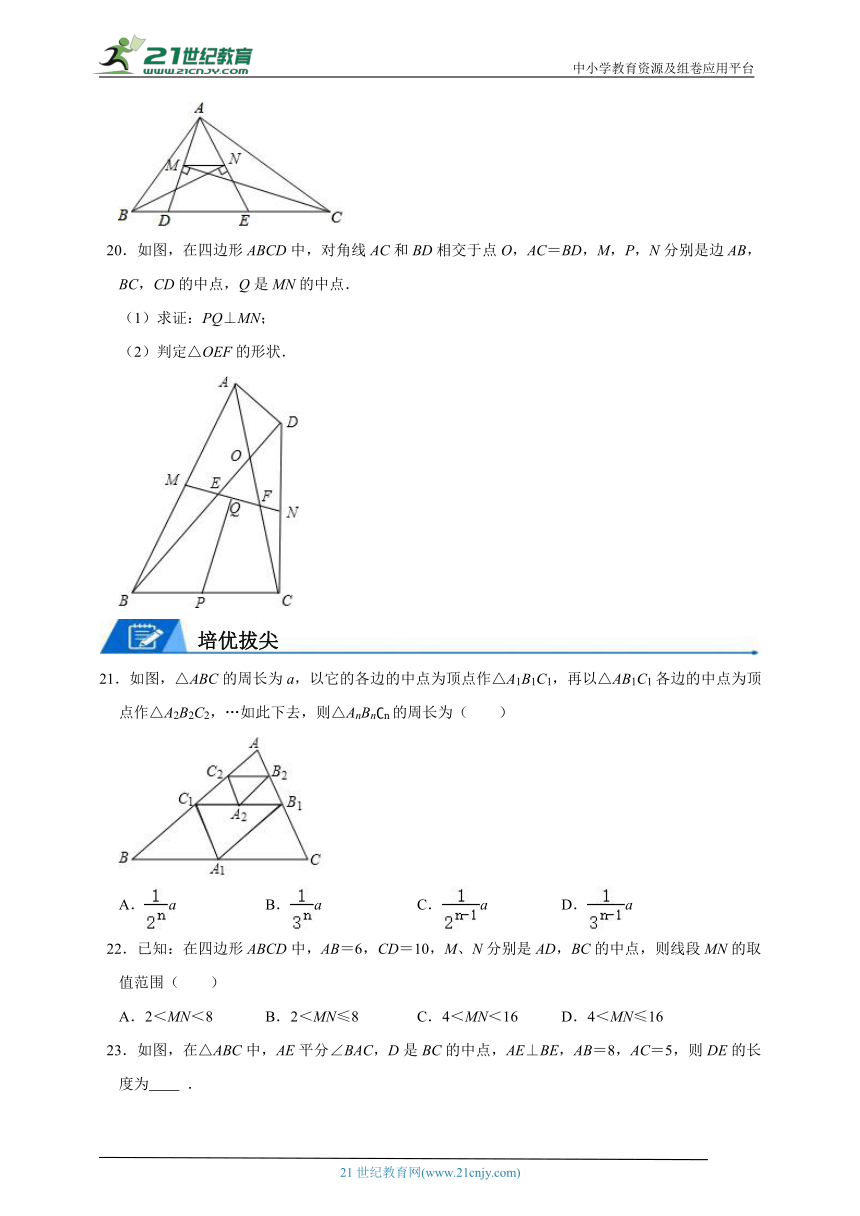
20.如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.
(1)求证:PQ⊥MN;
(2)判定△OEF的形状.
21.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
22.已知:在四边形ABCD中,AB=6,CD=10,M、N分别是AD,BC的中点,则线段MN的取值范围( )
A.2<MN<8 B.2<MN≤8 C.4<MN<16 D.4<MN≤16
23.如图,在△ABC中,AE平分∠BAC,D是BC的中点,AE⊥BE,AB=8,AC=5,则DE的长度为 .
24.如图,在Rt△ABC中,∠C=90°,点D是AB中点,点E在AC上.连结DE,且DE平分△ABC的周长.若DE=2,则BC的长为 .
25.【问题初探】
(1)全省数学教研活动示范课中,张老师给出如下问题:
如图①所示,四边形ABCD,点M和点N分别是边DC和边AB上的中点,点P是对角线BD的中点,AD=BC.求证:∠PMN=∠PNM.
结合图①,写出完整的证明过程.
【问题再探】
(2)张老师又给出如下问题:
如图②所示,如果在一个四边形ABCD中,点P和点Q分别为边AB和边CD的中点,且∠A+∠ABC=90°,BC=8,AD=10,求PQ两点的距离.
26.(1)如图1,在四边形ADBC中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE.
答案与解析
1.如图,在△ABC中,AC=BC,DE为△ABC的中位线,连接CD.若∠B=68°,则∠EDC的度数为( )
A.20° B.22° C.32° D.34°
【点拨】根据等腰三角形的性质求出∠A,根据三角形内角和定理求出∠ACB,根据等腰三角形的三线合一求出∠DCB,根据三角形中位线定理得到DE∥BC,根据平行线的性质解答即可.
【解析】解:在△ABC中,AC=BC,∠B=68°,
∴∠A=∠B=68°,
∴∠ACB=180°﹣68°×2=44°,
∵AC=BC,AD=DB,
∴∠DCB=∠ACB=22°,
∵DE为△ABC的中位线,
∴DE∥BC,
∴∠EDC=∠DCB=22°,
故选:B.
【点睛】本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形中位线平行于第三边是解题的关键.
2.如图,在△ABC中,AB=AC=3,AE⊥BC,垂足为点E,D是AC上一点,连接BD,F是BD的中点,当EF=1时,AD的长为( )
A. B.2 C.1 D.
【点拨】由等腰三角形的性质证得AE=CE,根据三角形中位线定理得到CD=2,即可求得答案.
【解析】解:∵AB=AC=3,AE⊥BC,
∴AE=CE,
∵F是BD的中点,
∴EF是△BCD的中位线,
∴EF=CD,
∵EF=1,
∴CD=2,
∴AD=AC﹣CD=3﹣2=1.
故选:C.
【点睛】本题主要考查了等腰三角形的性质和三角形中位线定理,熟练掌握性质定理是解决问题的关键.
3.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为( )
A.6.5cm B.34cm C.26cm D.52cm
【点拨】根据三角形中位线定理分别求出三边长,根据三角形的周长公式计算即可.
【解析】解:∵三角形的三条中位线长分别为3cm,4cm,6cm,
∴三角形的三边长分别为6cm,8cm,12cm,
∴原三角形的周长为:6+8+12=26(cm),
故选:C.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
4.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.3 B.2 C. D.4
【点拨】利用中位线定理,得到DE∥AB,根据平行线的性质,可得∠EDC=∠ABC,再利用角平分线的性质和三角形内角外角的关系,得到DF=DB,进而求出DF的长.
【解析】解:在△ABC中,D、E分别是BC、AC的中点,
∴DE∥AB,
∴∠EDC=∠ABC.
∵BF平分∠ABC,
∴∠EDC=2∠FBD.
在△BDF中,∠EDC=∠FBD+∠BFD,
∴∠DBF=∠DFB,
∴FD=BD=BC=×6=3.
故选:A.
【点睛】本题考查了三角形中位线定理和等腰三角形的判定于性质.三角形的中位线平行于第三边,当出现角平分线,平行线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.
5.如图,△DEF的三个顶点D,E,F分别为△ABC三边AB,AC,BC的中点,若△DEF的面积S△DEF=6,则△ABC的面积为( )
A.18 B.20 C.24 D.30
【点拨】根据三角形中位线定理得到DE∥BC,DE=BC=BF,得到四边形DBFE为平行四边形,根据平行四边形的性质计算即可.
【解析】解:∵D,E分别为边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC=BF,
∴四边形DBFE为平行四边形,
∴S△DBF=S△DEF=6,
同理可得:S△ECF=S△ADE=S△DEF=6,
∴S△ABC=6×4=24,
故选:C.
【点睛】本题考查的是三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半.
6.如图,在△ABC中,点D,E分别是边BC,AB的中点,若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
【点拨】根据三角形的面积公式即可得到结论.
【解析】解:由题意可得:S△ABD=S△ABC=4,
∵E是AB的中点,
∴S△BDE=S△ABD=4=2,
故选:A.
【点睛】本题考查了三角形的中线,三角形的面积的计算,正确的识别图形是解题的关键.
7.在△ABC中,点D,E分别是AB,AC的中点,如图1,2的两种作辅助线的作法:
作法一:延长DE到点F,使EF=DE,连接DC,AF,FC. 作法二:过点E作GE∥AB,过点A作AF∥BC,GE与AF交于点F.
其中能够用来证明三角形中位线定理的是( )
A.作法一和作法二都可以 B.作法一和作法二都不可以
C.作法一可以,作法二不可以 D.作法一不可以,作法二可以
【点拨】根据平行四边形的判定定理和性质定理判断作法一;证明△AEF≌△CEG,根据全等三角形的性质得到AF=CG,EF=EG,再根据平行四边形的判定定理和性质定理判断作法二.
【解析】解:作法二:∵AF∥BC,
∴∠EAF=∠C,∠F=∠CGF,
在△AEF和△CEG中,
,
∴△AEF≌△CEG(AAS),
∴AF=CG,EF=EG,
∵AF∥BG,AB∥FG,
∴四边形ABGF是平行四边形,
∴AB=FG,
∵BD=AB,GE=FG,
∴BD=EG,AF=BG,
∵BD∥EG,
∴四边形DBGE是平行四边形,
∴DE∥BG,DE=BG=AF=CG,
∴DE∥BC,DE=BC;
作法一:∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,
∴AD=CF,AD∥CF,
∵AD=BD,
∴BD=CF,BD∥CF,
∴四边形DBCF是平行四边形,
∴DF∥BC,DF=BC,
∴DE∥BC,DE=DF=BC;
∴作法一和作法二都可以,
故选:A.
【点睛】本题考查的是三角形中位线定理的证明,掌握平行四边形的判定和性质、全等三角形的判定和性质是解题的关键.
8.如图,在△ABC中,点D,E,F分别为AB,BC,AC边的中点,AG⊥BC于点G,DE=5,则线段FG的长为( )
A. B. C.5 D.4
【点拨】根据三角形中位线定理求出AC,再根据直角三角形斜边上的中线的性质解答.
【解析】解:∵点D,E分别为AB,BC边的中点,
∴DE是△ABC的中位线,
∴,
∵AG⊥BC,点F为AC边的中点,
∴.
故选:C.
【点睛】本题考查三角形的中位线定理和,关键是根据三角形中位线定理求出AC.
9.已知Rt△ABC,∠A=90°,AB=5,AC=12,点E、F分别是AB、AC的中点,则EF= 6.5 .
【点拨】根据勾股定理求出BC,再根据三角形中位线定理计算即可.
【解析】解:在Rt△ABC,∠A=90°,AB=5,AC=12,
由勾股定理得:BC===13,
∵点E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴EF=BC=6.5,
故答案为:6.5.
【点睛】本题考查的是勾股定理、三角形中位线定理,掌握三角形中位线等于第三边的一半是解题的关键.
10.如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= 60 °.
【点拨】根据直角三角形的性质、三角形的外角的性质、三角形中位线定理计算即可.
【解析】解:在Rt△ACD中,
∵点O是AC中点,
∴OD=AO,
∴∠ADO=∠CAD=20°,
∴∠DOC=40°,
∵E为BC的中点,点O是AC中点,
∴OE∥AB,
∴∠COE=∠CAB=20°,
∴∠DOE=60°,
故答案为:60.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
11.如图,CD是△ABC的中线,E,F分别是AC,CD的中点,BD=4,则EF的长为 2 .
【点拨】先利用中位线性质求得,再由中线知AD=BD,即可解答;
【解析】解:∵E,F分别是AC,CD的中点,
∴EF是△ADC的中位线,
∴EF=AD,
∵CD是△ABC的中线,
∴AD=BD=4,
∴,
故答案为:2.
【点睛】此题考查了三角形的中线和中位线,熟练掌握中位线的性质是解题的关键.
12.如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= 1 .
【点拨】根据三角形中位线定理得到DE=BC=3,DE∥BC,根据角平分线的定义、平行线的性质得到∠DBF=∠DFB,得到DF=BD=2,计算即可.
【解析】解:∵点D、E分别为AB,AC的中点,AB=4,
∴DE是△ABC的中位线,BD=AB=2,
∴DE=BC=3,DE∥BC,
∴∠DFB=∠FBC,
∵BF平分∠ABC,
∴∠DFB=∠FBC,
∴∠DBF=∠DFB,
∴DF=BD=2,
∴EF=DE﹣DF=3﹣2=1,
故答案为:1.
【点睛】本题主要考查三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半.
13.如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
【点拨】(1)先根据平行四边形的性质得到AD=BC,AD∥BC,再证明AF=CE,然后根据平行四边形的判定方法得到结论;
(2)先根据平行四边形的性质得到OA=OC,则可判断OF为△ACD的中位线,然后根据三角形中位线定理求解.
【解析】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∵点E、F分别为线段BC、AD的中点,
∴AF=AD,CE=BC,
∴AF=CE,
∵AF∥CE,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为平行四边形,
∴OA=OC,
∵AF=DF,
∴OF为△ACD的中位线,
∴CD=2OF=2×3=6.
【点睛】本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.也考查了平行四边形的判定与性质.
14.如图,在△ABC中,∠ABC=90°,点D,E分别是AC,BC的中点,连接DB,DE,过点E作EF∥DB,交AB的延长线于点F.
(1)证明:BF=DE;
(2)若BD=5,DE=3,求BC的长.
【点拨】(1)根据点D,E分别是AC,BC的中点,得出DE是△ABC的中位线,从而证明四边形BDEF是平行四边形,即可证明;
(2)根据直角三角形的性质得出.AC=10.根据三角形的中位线定理得出AB=6.在Rt△ABC中,由勾股定理即可求解.
【解析】(1)证明:∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴.
又∵EF∥DB,
∴四边形BDEF是平行四边形,
∴BF=DE.
(2)解:∵点D是AC的中点,∠ABC=90°,
∴.
又∵BD=5,
∴AC=10.
∵DE=3,
∴AB=6.
在Rt△ABC中,由勾股定理,得.
【点睛】本题主要考查了三角形中位线定理,勾股定理,平行四边形的判定与性质,熟练掌握三角形中位线定理是解题关键.
15.在等腰三角形ABC中,∠BAC=80°,AB=AC=4,CD平分∠ACB,AE⊥CD于点E,过点E作EF∥BC交AC于点F.
(1)求∠AEF的度数;
(2)若G是BC的中点,连接FG,求FG的长.
【点拨】(1)由角平分线的定义,平行线的性质,直角三角形的性质可得∠EAC=∠AEF,进而解答即可.
(2)由角平分线的定义及平行线的性质可得∠ACD=∠FEC,即可证明EF=CF,再利用直角三角形的性质可证明AF=CF,即可得GF是△ABC的中位线,进而可证明结论.
【解析】解:(1)∵CD平分∠ACB,
∴∠ACD=∠BCD,
∵EF∥BC,
∴∠FEC=∠BCD,
∴∠ACD=∠FEC,
∴EF=CF,
∵AE⊥CD,
∴∠AEC=90°,
∴∠EAC+∠ACD=90°,∠AEF+∠FEC=90°,
∴∠EAC=∠AEF,
∵∠BAC=80°,AB=AC=4,
∴∠ACB=∠ABC=50°,
∵EF∥BC,
∴∠AFE=50°,
∴∠AEF=∠EAC=65°;
(2)∵∠EAC=∠AEF,
∴AF=EF,
∴AF=CF,
∵G是BC的中点,
∴GF是△ABC的中位线,
∴FG=AB==2.
【点睛】本题主要考查角平分线的定义,平行线的性质,等腰三角形的判定,直角三角形的性质,三角形的中位线等知识的综合运用,证明GF是△ABC的中位线是解题的关键.
16.如图,△ABC中,AB=8,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,若EF=1,则边AC的长度等于( )
A.4 B.5 C.6 D.7
【点拨】判定△AGC是等腰三角形,推出FG=FC,得到EF是△CBG的中位线,推出BG=2EF=2,求出AG=6,即可得到AC的长.
【解析】解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵CG⊥AD,
∴∠AFG=∠AFC,
∴∠AGC=∠ACG,
∴AG=AC,
∵AD⊥CG,
∴FG=FC,
∵AD是△ABC的中线,
∴BE=CE,
∴EF是△CBG的中位线,
∴BG=2EF=2,
∴AG=AB﹣BG=8﹣2=6,
∴AC=AG=6.
故选:C.
【点睛】本题考查三角形中位线定理,等腰三角形的性质,关键是判定△AGC是等腰三角形,由等腰三角形的性质推出CF=FG,判定EF是△CBG的中位线.
17.如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=16,AD=CD=10,点M,N分别为BC,AB上的动点(含端点),E,F分别为DM,MN的中点,则EF长度的最小值是( )
A.4.5 B.4 C.5.5 D.6.5
【点拨】作DH⊥AB于H,连接DN,得到BH=CD=5,得到AH=3,根据勾股定理求出DH,根据三角形中位线定理解答.
【解析】解:作DH⊥AB于H,连接DN,
则四边形DHBC为矩形,
∴BH=CD=10,
∴AH=6,
∵E、F分别为DM、MN的中点,
∴EF=DN,
在Rt△ADH中,DH==8,
当点N与点H重合,DN最小,此时EF最小,
∴EF长度的最小值=DN=4,
故选:B.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
18.如图,在△ABC中,点D,E分别是边AB,BC的中点,连结DE,点F在DE上,连结FB,FC,若FB⊥FC,BC=6,DF=1,则AC的长为 8 .
【点拨】根据直角三角形斜边上的中线的性质求出EF,进而求出DE,再根据三角形中位线定理解答即可.
【解析】解:∵FB⊥FC,
∴∠BFC=90°,
∵E是边BC的中点,BC=6,
∴EF=BC=3,
∴DE=DF+EF=4,
∵点D,E分别是边AB,BC的中点,
∴AC=2DE=8,
故答案为:8.
【点睛】本题考查的是三角形中位线定理、直角三角形斜边上的中线的性质,熟记三角形中位线等于第三边的一半是解题的关键.
19.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
【点拨】证明△BNA≌△BNE,得到BA=BE,即△BAE是等腰三角形,同理△CAD是等腰三角形,根据题意求出DE,根据三角形中位线定理计算即可.
【解析】解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
.
∴△BNA≌△BNE(ASA),
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MN=DE=.
故答案为:.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
20.如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.
(1)求证:PQ⊥MN;
(2)判定△OEF的形状.
【点拨】(1)连接PM,PN,由三角形中位线定理可证明△PMN是等腰三角形,再由等腰三角形的性质即可证明PQ⊥MN;
(2)△OEF的形状是等腰三角形,由(1)中的条件可证明∠PMN=∠EFO,∠OEF=∠FNP,又因为∠PMN=∠PNM,所以∠EFO=∠OEF,所以△OEF是等腰三角形.
【解析】(1)证明:
∵M,P分别是边AB,BC的中点,
∴AM=BM,BP=CP,
∴PM=AC
∵DN=CN,BP=CP,
∴PN=BD.
又∵AC=BD,
∴PM=PN,
∴P在MN的中垂线上,
∵MQ=NQ,
∴PQ⊥MN;
(2)△OEF的形状是等腰三角形,
理由如下:
∵PM∥AC,
∴∠PMN=∠EFO,
∵PN∥BD,
∴∠OEF=∠FNP,
又∵∠PMN=∠PNM,
∴∠EFO=∠OEF,
∴△OEF的形状是等腰三角形.
【点睛】本题考查了三角形中位线定理、等腰三角形的判定和性质,解题的关键是正确添加辅助线,利用三角形中位线定理证明PM=PN.
21.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
【点拨】根据三角形中位线定理得到△A1B1C1的周长=a,△A2B2C2的周长=a=a,总结规律,根据规律解答即可.
【解析】解:∵点A1、B1、C1分别为BC、AC、AB的中点,
∴B1C1=BC,A1C1=AC,A1B1=AB,
∴△A1B1C1的周长=a,
同理,△A2B2C2的周长=a=a,
……
则△AnBn n的周长=a,
故选:A.
【点睛】本题考查的是三角形中位线定理,正确找出三角形的周长的变化规律是解题的关键.
22.已知:在四边形ABCD中,AB=6,CD=10,M、N分别是AD,BC的中点,则线段MN的取值范围( )
A.2<MN<8 B.2<MN≤8 C.4<MN<16 D.4<MN≤16
【点拨】当AB∥CD时,MN最短,利用中位线定理可得MN的最长值,作出辅助线,利用三角形中位线及三边关系可得MN的其他取值范围.
【解析】解:连接BD,过M作MG∥AB,连接NG.
∵M是边AD的中点,AB=6,MG∥AB,
∴MG是△ABD的中位线,BG=GD,MG=AB=×6=3.
∵N是BC的中点,BG=GD,CD=10,
∴NG是△BCD的中位线,NG=CD=×10=5,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,即5﹣3<MN<5+3,
∴2<MN<8,
当MN=MG+NG,即MN=8时,四边形ABCD是梯形,
故线段MN长的取值范围是2<MN≤8.
故选:B.
【点睛】本题主要考查了三角形中位线定理,解答此题的关键是根据题意作出辅助线,利用三角形中位线定理及三角形三边关系解答.
23.如图,在△ABC中,AE平分∠BAC,D是BC的中点,AE⊥BE,AB=8,AC=5,则DE的长度为 .
【点拨】延长AC,BE,相交于点F,证明△ABE≌△AFE,得出BE=EF,AB=AF,然后利用三角形中位线定理求解即可.
【解析】解:延长AC,BE,相交于点F,
∵AE平分∠BAC,
∴∠BAE=∠FAE,
∵AE⊥BE,
∴∠AEB=∠AEF=90°,
又AE=AE,
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,
∵AB=8,AC=5,
∴CF=AF﹣AC=AB﹣AC=3,
∵D是BC的中点,BE=EF,
∴DE是△BCF的中位线,
∴DE=CF=.
故答案为:.
【点睛】本题考查了三角形中位线定理,全等三角形的判定与性质等知识,正确进行计算是解题关键.
24.如图,在Rt△ABC中,∠C=90°,点D是AB中点,点E在AC上.连结DE,且DE平分△ABC的周长.若DE=2,则BC的长为 2 .
【点拨】延长AC至F,使得CF=BC,根据勾股定理求出AF,根据题意得到E是BF的中点,根据三角形中位线定理计算,得到答案.
【解析】解:延长AC至F,使得CF=BC,
∵∠ACB=90°,
∴∠BCF=90°,
在Rt△BCF中,BF==BC,
∵D是AB边中点,DE平分△ABC的周长,
∴BC+CE=AE,
∴EF=EA,即E是AF的中点,
∵D为AB的中点,
∴DE是△ABF的中位线,
∴DE=BF,即BF=2DE=4,
∴BF=BC=4,
∴BC=2.
故答案为:2.
【点睛】本题考查的是三角形中位线定理、勾股定理的运用,掌握三角形中位线定理,正确作出辅助线是解题的关键.
25.【问题初探】
(1)全省数学教研活动示范课中,张老师给出如下问题:
如图①所示,四边形ABCD,点M和点N分别是边DC和边AB上的中点,点P是对角线BD的中点,AD=BC.求证:∠PMN=∠PNM.
结合图①,写出完整的证明过程.
【问题再探】
(2)张老师又给出如下问题:
如图②所示,如果在一个四边形ABCD中,点P和点Q分别为边AB和边CD的中点,且∠A+∠ABC=90°,BC=8,AD=10,求PQ两点的距离.
【点拨】(1)如图①,利用中位线定理得到,,由AD=BC得到PM=PN,即可得到结论;
(2)如图②,连接BD,取BD的中点G,连接PG,QG,由三角形中位线定理得到PG=5,QG=4,PG∥AD,则∠BPG=∠A,∠DGQ=∠DBC,进一步得到∠PGQ=90°,根据勾股定理即可得到.
【解析】(1)证明:∵点P,N分别是BD,AB的中点,
∴PN是△ABD的中位线,
∴,
∵点P,M分别是BD,CD的中点,
∴PM是△BCD的中位线,
∴,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM;
(2)解:如图②,连接BD,取BD的中点G,连接PG,QG,
∵点P,G分别是AB,BD的中点,
∴PG是△ABD的中位线,
∴,
同理:QG是△BCD的中位线,
∴,
∵PG是△ABD的中位线,
∴PG∥AD,
∴∠BPG=∠A,
∵QG是△BCD的中位线,
∴QG∥BC,
∴∠DGQ=∠DBC,
∴∠PGQ=∠PGD+∠DGQ=∠BPG+∠ABD+∠DBC=∠BPG+∠ABC=∠A+∠ABC,
∵∠A+∠ABC=90°,
∴∠PGQ=90°,
根据勾股定理得,.
【点睛】此题考查了三角形中位线定理、勾股定理,掌握等腰三角形的性质是解题的关键.
26.(1)如图1,在四边形ADBC中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE.
【点拨】(1)作出两条中位线,根据中位线定理,找到相等的同位角和线段,进而判断出三角形的形状.
(2)连接BD,取DB的中点H,连接EH,FH,根据三角形中位线定理得到EH∥AB,EH=AB,根据平行线的性质证明.
【解析】解:(1)△OMN是等腰三角形,理由如下:
如图,取BD的中点H,连接HE,HF,
∵E,F分别是BC,AD的中点,
∴HF∥AB,HE∥CD,,,
∵AB=CD,
∴HF=HE,
∴∠HFE=∠HEF,
∵HF∥AB,HE∥CD,
∴∠HFE=∠ONM,∠HEF=∠OMN,
∴∠ONM=∠OMN,
∴OM=ON,
∴△OMN是等腰三角形.
(2)如图,连接BD,取BD的中点H,连接HE,HF,
∴HF∥CN,HE∥BM,,,
∵AB=CD,
∴HF=HE,
∴∠HEF=∠HFE,
∵HF∥CN,HE∥BM,
∴∠HEF=∠BME,∠HFE=∠CNE,
∴∠BME=∠CNE.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.5 三角形的中位线 同步分层作业
1.如图,在△ABC中,AC=BC,DE为△ABC的中位线,连接CD.若∠B=68°,则∠EDC的度数为( )
A.20° B.22° C.32° D.34°
2.如图,在△ABC中,AB=AC=3,AE⊥BC,垂足为点E,D是AC上一点,连接BD,F是BD的中点,当EF=1时,AD的长为( )
A. B.2 C.1 D.
3.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为( )
A.6.5cm B.34cm C.26cm D.52cm
4.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.3 B.2 C. D.4
5.如图,△DEF的三个顶点D,E,F分别为△ABC三边AB,AC,BC的中点,若△DEF的面积S△DEF=6,则△ABC的面积为( )
A.18 B.20 C.24 D.30
6.如图,在△ABC中,点D,E分别是边BC,AB的中点,若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
7.在△ABC中,点D,E分别是AB,AC的中点,如图1,2的两种作辅助线的作法:
作法一:延长DE到点F,使EF=DE,连接DC,AF,FC. 作法二:过点E作GE∥AB,过点A作AF∥BC,GE与AF交于点F.
其中能够用来证明三角形中位线定理的是( )
A.作法一和作法二都可以 B.作法一和作法二都不可以
C.作法一可以,作法二不可以 D.作法一不可以,作法二可以
8.如图,在△ABC中,点D,E,F分别为AB,BC,AC边的中点,AG⊥BC于点G,DE=5,则线段FG的长为( )
A. B. C.5 D.4
9.已知Rt△ABC,∠A=90°,AB=5,AC=12,点E、F分别是AB、AC的中点,则EF= .
10.如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= °.
11.如图,CD是△ABC的中线,E,F分别是AC,CD的中点,BD=4,则EF的长为 .
12.如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= .
13.如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
14.如图,在△ABC中,∠ABC=90°,点D,E分别是AC,BC的中点,连接DB,DE,过点E作EF∥DB,交AB的延长线于点F.
(1)证明:BF=DE;
(2)若BD=5,DE=3,求BC的长.
15.在等腰三角形ABC中,∠BAC=80°,AB=AC=4,CD平分∠ACB,AE⊥CD于点E,过点E作EF∥BC交AC于点F.
(1)求∠AEF的度数;
(2)若G是BC的中点,连接FG,求FG的长.
16.如图,△ABC中,AB=8,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,若EF=1,则边AC的长度等于( )
A.4 B.5 C.6 D.7
17.如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=16,AD=CD=10,点M,N分别为BC,AB上的动点(含端点),E,F分别为DM,MN的中点,则EF长度的最小值是( )
A.4.5 B.4 C.5.5 D.6.5
18.如图,在△ABC中,点D,E分别是边AB,BC的中点,连结DE,点F在DE上,连结FB,FC,若FB⊥FC,BC=6,DF=1,则AC的长为 .
19.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
20.如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.
(1)求证:PQ⊥MN;
(2)判定△OEF的形状.
21.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
22.已知:在四边形ABCD中,AB=6,CD=10,M、N分别是AD,BC的中点,则线段MN的取值范围( )
A.2<MN<8 B.2<MN≤8 C.4<MN<16 D.4<MN≤16
23.如图,在△ABC中,AE平分∠BAC,D是BC的中点,AE⊥BE,AB=8,AC=5,则DE的长度为 .
24.如图,在Rt△ABC中,∠C=90°,点D是AB中点,点E在AC上.连结DE,且DE平分△ABC的周长.若DE=2,则BC的长为 .
25.【问题初探】
(1)全省数学教研活动示范课中,张老师给出如下问题:
如图①所示,四边形ABCD,点M和点N分别是边DC和边AB上的中点,点P是对角线BD的中点,AD=BC.求证:∠PMN=∠PNM.
结合图①,写出完整的证明过程.
【问题再探】
(2)张老师又给出如下问题:
如图②所示,如果在一个四边形ABCD中,点P和点Q分别为边AB和边CD的中点,且∠A+∠ABC=90°,BC=8,AD=10,求PQ两点的距离.
26.(1)如图1,在四边形ADBC中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE.
答案与解析
1.如图,在△ABC中,AC=BC,DE为△ABC的中位线,连接CD.若∠B=68°,则∠EDC的度数为( )
A.20° B.22° C.32° D.34°
【点拨】根据等腰三角形的性质求出∠A,根据三角形内角和定理求出∠ACB,根据等腰三角形的三线合一求出∠DCB,根据三角形中位线定理得到DE∥BC,根据平行线的性质解答即可.
【解析】解:在△ABC中,AC=BC,∠B=68°,
∴∠A=∠B=68°,
∴∠ACB=180°﹣68°×2=44°,
∵AC=BC,AD=DB,
∴∠DCB=∠ACB=22°,
∵DE为△ABC的中位线,
∴DE∥BC,
∴∠EDC=∠DCB=22°,
故选:B.
【点睛】本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形中位线平行于第三边是解题的关键.
2.如图,在△ABC中,AB=AC=3,AE⊥BC,垂足为点E,D是AC上一点,连接BD,F是BD的中点,当EF=1时,AD的长为( )
A. B.2 C.1 D.
【点拨】由等腰三角形的性质证得AE=CE,根据三角形中位线定理得到CD=2,即可求得答案.
【解析】解:∵AB=AC=3,AE⊥BC,
∴AE=CE,
∵F是BD的中点,
∴EF是△BCD的中位线,
∴EF=CD,
∵EF=1,
∴CD=2,
∴AD=AC﹣CD=3﹣2=1.
故选:C.
【点睛】本题主要考查了等腰三角形的性质和三角形中位线定理,熟练掌握性质定理是解决问题的关键.
3.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为( )
A.6.5cm B.34cm C.26cm D.52cm
【点拨】根据三角形中位线定理分别求出三边长,根据三角形的周长公式计算即可.
【解析】解:∵三角形的三条中位线长分别为3cm,4cm,6cm,
∴三角形的三边长分别为6cm,8cm,12cm,
∴原三角形的周长为:6+8+12=26(cm),
故选:C.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
4.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是( )
A.3 B.2 C. D.4
【点拨】利用中位线定理,得到DE∥AB,根据平行线的性质,可得∠EDC=∠ABC,再利用角平分线的性质和三角形内角外角的关系,得到DF=DB,进而求出DF的长.
【解析】解:在△ABC中,D、E分别是BC、AC的中点,
∴DE∥AB,
∴∠EDC=∠ABC.
∵BF平分∠ABC,
∴∠EDC=2∠FBD.
在△BDF中,∠EDC=∠FBD+∠BFD,
∴∠DBF=∠DFB,
∴FD=BD=BC=×6=3.
故选:A.
【点睛】本题考查了三角形中位线定理和等腰三角形的判定于性质.三角形的中位线平行于第三边,当出现角平分线,平行线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.
5.如图,△DEF的三个顶点D,E,F分别为△ABC三边AB,AC,BC的中点,若△DEF的面积S△DEF=6,则△ABC的面积为( )
A.18 B.20 C.24 D.30
【点拨】根据三角形中位线定理得到DE∥BC,DE=BC=BF,得到四边形DBFE为平行四边形,根据平行四边形的性质计算即可.
【解析】解:∵D,E分别为边AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=BC=BF,
∴四边形DBFE为平行四边形,
∴S△DBF=S△DEF=6,
同理可得:S△ECF=S△ADE=S△DEF=6,
∴S△ABC=6×4=24,
故选:C.
【点睛】本题考查的是三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半.
6.如图,在△ABC中,点D,E分别是边BC,AB的中点,若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
【点拨】根据三角形的面积公式即可得到结论.
【解析】解:由题意可得:S△ABD=S△ABC=4,
∵E是AB的中点,
∴S△BDE=S△ABD=4=2,
故选:A.
【点睛】本题考查了三角形的中线,三角形的面积的计算,正确的识别图形是解题的关键.
7.在△ABC中,点D,E分别是AB,AC的中点,如图1,2的两种作辅助线的作法:
作法一:延长DE到点F,使EF=DE,连接DC,AF,FC. 作法二:过点E作GE∥AB,过点A作AF∥BC,GE与AF交于点F.
其中能够用来证明三角形中位线定理的是( )
A.作法一和作法二都可以 B.作法一和作法二都不可以
C.作法一可以,作法二不可以 D.作法一不可以,作法二可以
【点拨】根据平行四边形的判定定理和性质定理判断作法一;证明△AEF≌△CEG,根据全等三角形的性质得到AF=CG,EF=EG,再根据平行四边形的判定定理和性质定理判断作法二.
【解析】解:作法二:∵AF∥BC,
∴∠EAF=∠C,∠F=∠CGF,
在△AEF和△CEG中,
,
∴△AEF≌△CEG(AAS),
∴AF=CG,EF=EG,
∵AF∥BG,AB∥FG,
∴四边形ABGF是平行四边形,
∴AB=FG,
∵BD=AB,GE=FG,
∴BD=EG,AF=BG,
∵BD∥EG,
∴四边形DBGE是平行四边形,
∴DE∥BG,DE=BG=AF=CG,
∴DE∥BC,DE=BC;
作法一:∵AE=EC,DE=EF,
∴四边形ADCF是平行四边形,
∴AD=CF,AD∥CF,
∵AD=BD,
∴BD=CF,BD∥CF,
∴四边形DBCF是平行四边形,
∴DF∥BC,DF=BC,
∴DE∥BC,DE=DF=BC;
∴作法一和作法二都可以,
故选:A.
【点睛】本题考查的是三角形中位线定理的证明,掌握平行四边形的判定和性质、全等三角形的判定和性质是解题的关键.
8.如图,在△ABC中,点D,E,F分别为AB,BC,AC边的中点,AG⊥BC于点G,DE=5,则线段FG的长为( )
A. B. C.5 D.4
【点拨】根据三角形中位线定理求出AC,再根据直角三角形斜边上的中线的性质解答.
【解析】解:∵点D,E分别为AB,BC边的中点,
∴DE是△ABC的中位线,
∴,
∵AG⊥BC,点F为AC边的中点,
∴.
故选:C.
【点睛】本题考查三角形的中位线定理和,关键是根据三角形中位线定理求出AC.
9.已知Rt△ABC,∠A=90°,AB=5,AC=12,点E、F分别是AB、AC的中点,则EF= 6.5 .
【点拨】根据勾股定理求出BC,再根据三角形中位线定理计算即可.
【解析】解:在Rt△ABC,∠A=90°,AB=5,AC=12,
由勾股定理得:BC===13,
∵点E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴EF=BC=6.5,
故答案为:6.5.
【点睛】本题考查的是勾股定理、三角形中位线定理,掌握三角形中位线等于第三边的一半是解题的关键.
10.如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= 60 °.
【点拨】根据直角三角形的性质、三角形的外角的性质、三角形中位线定理计算即可.
【解析】解:在Rt△ACD中,
∵点O是AC中点,
∴OD=AO,
∴∠ADO=∠CAD=20°,
∴∠DOC=40°,
∵E为BC的中点,点O是AC中点,
∴OE∥AB,
∴∠COE=∠CAB=20°,
∴∠DOE=60°,
故答案为:60.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
11.如图,CD是△ABC的中线,E,F分别是AC,CD的中点,BD=4,则EF的长为 2 .
【点拨】先利用中位线性质求得,再由中线知AD=BD,即可解答;
【解析】解:∵E,F分别是AC,CD的中点,
∴EF是△ADC的中位线,
∴EF=AD,
∵CD是△ABC的中线,
∴AD=BD=4,
∴,
故答案为:2.
【点睛】此题考查了三角形的中线和中位线,熟练掌握中位线的性质是解题的关键.
12.如图,点D、E分别为AB,AC的中点,BF平分∠ABC交DE于点F,若AB=4,BC=6,则EF= 1 .
【点拨】根据三角形中位线定理得到DE=BC=3,DE∥BC,根据角平分线的定义、平行线的性质得到∠DBF=∠DFB,得到DF=BD=2,计算即可.
【解析】解:∵点D、E分别为AB,AC的中点,AB=4,
∴DE是△ABC的中位线,BD=AB=2,
∴DE=BC=3,DE∥BC,
∴∠DFB=∠FBC,
∵BF平分∠ABC,
∴∠DFB=∠FBC,
∴∠DBF=∠DFB,
∴DF=BD=2,
∴EF=DE﹣DF=3﹣2=1,
故答案为:1.
【点睛】本题主要考查三角形中位线定理,三角形的中位线平行于第三边,且等于第三边的一半.
13.如图,四边形ABCD为平行四边形,线段AC为对角线,点E、F分别为线段BC、AD的中点,连接EF交AC于点O.
(1)求证:四边形AECF为平行四边形;
(2)若OF=3,求CD的长.
【点拨】(1)先根据平行四边形的性质得到AD=BC,AD∥BC,再证明AF=CE,然后根据平行四边形的判定方法得到结论;
(2)先根据平行四边形的性质得到OA=OC,则可判断OF为△ACD的中位线,然后根据三角形中位线定理求解.
【解析】(1)证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∵点E、F分别为线段BC、AD的中点,
∴AF=AD,CE=BC,
∴AF=CE,
∵AF∥CE,
∴四边形AECF为平行四边形;
(2)解:∵四边形AECF为平行四边形,
∴OA=OC,
∵AF=DF,
∴OF为△ACD的中位线,
∴CD=2OF=2×3=6.
【点睛】本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.也考查了平行四边形的判定与性质.
14.如图,在△ABC中,∠ABC=90°,点D,E分别是AC,BC的中点,连接DB,DE,过点E作EF∥DB,交AB的延长线于点F.
(1)证明:BF=DE;
(2)若BD=5,DE=3,求BC的长.
【点拨】(1)根据点D,E分别是AC,BC的中点,得出DE是△ABC的中位线,从而证明四边形BDEF是平行四边形,即可证明;
(2)根据直角三角形的性质得出.AC=10.根据三角形的中位线定理得出AB=6.在Rt△ABC中,由勾股定理即可求解.
【解析】(1)证明:∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴.
又∵EF∥DB,
∴四边形BDEF是平行四边形,
∴BF=DE.
(2)解:∵点D是AC的中点,∠ABC=90°,
∴.
又∵BD=5,
∴AC=10.
∵DE=3,
∴AB=6.
在Rt△ABC中,由勾股定理,得.
【点睛】本题主要考查了三角形中位线定理,勾股定理,平行四边形的判定与性质,熟练掌握三角形中位线定理是解题关键.
15.在等腰三角形ABC中,∠BAC=80°,AB=AC=4,CD平分∠ACB,AE⊥CD于点E,过点E作EF∥BC交AC于点F.
(1)求∠AEF的度数;
(2)若G是BC的中点,连接FG,求FG的长.
【点拨】(1)由角平分线的定义,平行线的性质,直角三角形的性质可得∠EAC=∠AEF,进而解答即可.
(2)由角平分线的定义及平行线的性质可得∠ACD=∠FEC,即可证明EF=CF,再利用直角三角形的性质可证明AF=CF,即可得GF是△ABC的中位线,进而可证明结论.
【解析】解:(1)∵CD平分∠ACB,
∴∠ACD=∠BCD,
∵EF∥BC,
∴∠FEC=∠BCD,
∴∠ACD=∠FEC,
∴EF=CF,
∵AE⊥CD,
∴∠AEC=90°,
∴∠EAC+∠ACD=90°,∠AEF+∠FEC=90°,
∴∠EAC=∠AEF,
∵∠BAC=80°,AB=AC=4,
∴∠ACB=∠ABC=50°,
∵EF∥BC,
∴∠AFE=50°,
∴∠AEF=∠EAC=65°;
(2)∵∠EAC=∠AEF,
∴AF=EF,
∴AF=CF,
∵G是BC的中点,
∴GF是△ABC的中位线,
∴FG=AB==2.
【点睛】本题主要考查角平分线的定义,平行线的性质,等腰三角形的判定,直角三角形的性质,三角形的中位线等知识的综合运用,证明GF是△ABC的中位线是解题的关键.
16.如图,△ABC中,AB=8,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,若EF=1,则边AC的长度等于( )
A.4 B.5 C.6 D.7
【点拨】判定△AGC是等腰三角形,推出FG=FC,得到EF是△CBG的中位线,推出BG=2EF=2,求出AG=6,即可得到AC的长.
【解析】解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵CG⊥AD,
∴∠AFG=∠AFC,
∴∠AGC=∠ACG,
∴AG=AC,
∵AD⊥CG,
∴FG=FC,
∵AD是△ABC的中线,
∴BE=CE,
∴EF是△CBG的中位线,
∴BG=2EF=2,
∴AG=AB﹣BG=8﹣2=6,
∴AC=AG=6.
故选:C.
【点睛】本题考查三角形中位线定理,等腰三角形的性质,关键是判定△AGC是等腰三角形,由等腰三角形的性质推出CF=FG,判定EF是△CBG的中位线.
17.如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=16,AD=CD=10,点M,N分别为BC,AB上的动点(含端点),E,F分别为DM,MN的中点,则EF长度的最小值是( )
A.4.5 B.4 C.5.5 D.6.5
【点拨】作DH⊥AB于H,连接DN,得到BH=CD=5,得到AH=3,根据勾股定理求出DH,根据三角形中位线定理解答.
【解析】解:作DH⊥AB于H,连接DN,
则四边形DHBC为矩形,
∴BH=CD=10,
∴AH=6,
∵E、F分别为DM、MN的中点,
∴EF=DN,
在Rt△ADH中,DH==8,
当点N与点H重合,DN最小,此时EF最小,
∴EF长度的最小值=DN=4,
故选:B.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
18.如图,在△ABC中,点D,E分别是边AB,BC的中点,连结DE,点F在DE上,连结FB,FC,若FB⊥FC,BC=6,DF=1,则AC的长为 8 .
【点拨】根据直角三角形斜边上的中线的性质求出EF,进而求出DE,再根据三角形中位线定理解答即可.
【解析】解:∵FB⊥FC,
∴∠BFC=90°,
∵E是边BC的中点,BC=6,
∴EF=BC=3,
∴DE=DF+EF=4,
∵点D,E分别是边AB,BC的中点,
∴AC=2DE=8,
故答案为:8.
【点睛】本题考查的是三角形中位线定理、直角三角形斜边上的中线的性质,熟记三角形中位线等于第三边的一半是解题的关键.
19.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为 .
【点拨】证明△BNA≌△BNE,得到BA=BE,即△BAE是等腰三角形,同理△CAD是等腰三角形,根据题意求出DE,根据三角形中位线定理计算即可.
【解析】解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
.
∴△BNA≌△BNE(ASA),
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MN=DE=.
故答案为:.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
20.如图,在四边形ABCD中,对角线AC和BD相交于点O,AC=BD,M,P,N分别是边AB,BC,CD的中点,Q是MN的中点.
(1)求证:PQ⊥MN;
(2)判定△OEF的形状.
【点拨】(1)连接PM,PN,由三角形中位线定理可证明△PMN是等腰三角形,再由等腰三角形的性质即可证明PQ⊥MN;
(2)△OEF的形状是等腰三角形,由(1)中的条件可证明∠PMN=∠EFO,∠OEF=∠FNP,又因为∠PMN=∠PNM,所以∠EFO=∠OEF,所以△OEF是等腰三角形.
【解析】(1)证明:
∵M,P分别是边AB,BC的中点,
∴AM=BM,BP=CP,
∴PM=AC
∵DN=CN,BP=CP,
∴PN=BD.
又∵AC=BD,
∴PM=PN,
∴P在MN的中垂线上,
∵MQ=NQ,
∴PQ⊥MN;
(2)△OEF的形状是等腰三角形,
理由如下:
∵PM∥AC,
∴∠PMN=∠EFO,
∵PN∥BD,
∴∠OEF=∠FNP,
又∵∠PMN=∠PNM,
∴∠EFO=∠OEF,
∴△OEF的形状是等腰三角形.
【点睛】本题考查了三角形中位线定理、等腰三角形的判定和性质,解题的关键是正确添加辅助线,利用三角形中位线定理证明PM=PN.
21.如图,△ABC的周长为a,以它的各边的中点为顶点作△A1B1C1,再以△AB1C1各边的中点为顶点作△A2B2C2,…如此下去,则△AnBn n的周长为( )
A.a B.a C.a D.a
【点拨】根据三角形中位线定理得到△A1B1C1的周长=a,△A2B2C2的周长=a=a,总结规律,根据规律解答即可.
【解析】解:∵点A1、B1、C1分别为BC、AC、AB的中点,
∴B1C1=BC,A1C1=AC,A1B1=AB,
∴△A1B1C1的周长=a,
同理,△A2B2C2的周长=a=a,
……
则△AnBn n的周长=a,
故选:A.
【点睛】本题考查的是三角形中位线定理,正确找出三角形的周长的变化规律是解题的关键.
22.已知:在四边形ABCD中,AB=6,CD=10,M、N分别是AD,BC的中点,则线段MN的取值范围( )
A.2<MN<8 B.2<MN≤8 C.4<MN<16 D.4<MN≤16
【点拨】当AB∥CD时,MN最短,利用中位线定理可得MN的最长值,作出辅助线,利用三角形中位线及三边关系可得MN的其他取值范围.
【解析】解:连接BD,过M作MG∥AB,连接NG.
∵M是边AD的中点,AB=6,MG∥AB,
∴MG是△ABD的中位线,BG=GD,MG=AB=×6=3.
∵N是BC的中点,BG=GD,CD=10,
∴NG是△BCD的中位线,NG=CD=×10=5,
在△MNG中,由三角形三边关系可知NG﹣MG<MN<MG+NG,即5﹣3<MN<5+3,
∴2<MN<8,
当MN=MG+NG,即MN=8时,四边形ABCD是梯形,
故线段MN长的取值范围是2<MN≤8.
故选:B.
【点睛】本题主要考查了三角形中位线定理,解答此题的关键是根据题意作出辅助线,利用三角形中位线定理及三角形三边关系解答.
23.如图,在△ABC中,AE平分∠BAC,D是BC的中点,AE⊥BE,AB=8,AC=5,则DE的长度为 .
【点拨】延长AC,BE,相交于点F,证明△ABE≌△AFE,得出BE=EF,AB=AF,然后利用三角形中位线定理求解即可.
【解析】解:延长AC,BE,相交于点F,
∵AE平分∠BAC,
∴∠BAE=∠FAE,
∵AE⊥BE,
∴∠AEB=∠AEF=90°,
又AE=AE,
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,
∵AB=8,AC=5,
∴CF=AF﹣AC=AB﹣AC=3,
∵D是BC的中点,BE=EF,
∴DE是△BCF的中位线,
∴DE=CF=.
故答案为:.
【点睛】本题考查了三角形中位线定理,全等三角形的判定与性质等知识,正确进行计算是解题关键.
24.如图,在Rt△ABC中,∠C=90°,点D是AB中点,点E在AC上.连结DE,且DE平分△ABC的周长.若DE=2,则BC的长为 2 .
【点拨】延长AC至F,使得CF=BC,根据勾股定理求出AF,根据题意得到E是BF的中点,根据三角形中位线定理计算,得到答案.
【解析】解:延长AC至F,使得CF=BC,
∵∠ACB=90°,
∴∠BCF=90°,
在Rt△BCF中,BF==BC,
∵D是AB边中点,DE平分△ABC的周长,
∴BC+CE=AE,
∴EF=EA,即E是AF的中点,
∵D为AB的中点,
∴DE是△ABF的中位线,
∴DE=BF,即BF=2DE=4,
∴BF=BC=4,
∴BC=2.
故答案为:2.
【点睛】本题考查的是三角形中位线定理、勾股定理的运用,掌握三角形中位线定理,正确作出辅助线是解题的关键.
25.【问题初探】
(1)全省数学教研活动示范课中,张老师给出如下问题:
如图①所示,四边形ABCD,点M和点N分别是边DC和边AB上的中点,点P是对角线BD的中点,AD=BC.求证:∠PMN=∠PNM.
结合图①,写出完整的证明过程.
【问题再探】
(2)张老师又给出如下问题:
如图②所示,如果在一个四边形ABCD中,点P和点Q分别为边AB和边CD的中点,且∠A+∠ABC=90°,BC=8,AD=10,求PQ两点的距离.
【点拨】(1)如图①,利用中位线定理得到,,由AD=BC得到PM=PN,即可得到结论;
(2)如图②,连接BD,取BD的中点G,连接PG,QG,由三角形中位线定理得到PG=5,QG=4,PG∥AD,则∠BPG=∠A,∠DGQ=∠DBC,进一步得到∠PGQ=90°,根据勾股定理即可得到.
【解析】(1)证明:∵点P,N分别是BD,AB的中点,
∴PN是△ABD的中位线,
∴,
∵点P,M分别是BD,CD的中点,
∴PM是△BCD的中位线,
∴,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM;
(2)解:如图②,连接BD,取BD的中点G,连接PG,QG,
∵点P,G分别是AB,BD的中点,
∴PG是△ABD的中位线,
∴,
同理:QG是△BCD的中位线,
∴,
∵PG是△ABD的中位线,
∴PG∥AD,
∴∠BPG=∠A,
∵QG是△BCD的中位线,
∴QG∥BC,
∴∠DGQ=∠DBC,
∴∠PGQ=∠PGD+∠DGQ=∠BPG+∠ABD+∠DBC=∠BPG+∠ABC=∠A+∠ABC,
∵∠A+∠ABC=90°,
∴∠PGQ=90°,
根据勾股定理得,.
【点睛】此题考查了三角形中位线定理、勾股定理,掌握等腰三角形的性质是解题的关键.
26.(1)如图1,在四边形ADBC中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE.
【点拨】(1)作出两条中位线,根据中位线定理,找到相等的同位角和线段,进而判断出三角形的形状.
(2)连接BD,取DB的中点H,连接EH,FH,根据三角形中位线定理得到EH∥AB,EH=AB,根据平行线的性质证明.
【解析】解:(1)△OMN是等腰三角形,理由如下:
如图,取BD的中点H,连接HE,HF,
∵E,F分别是BC,AD的中点,
∴HF∥AB,HE∥CD,,,
∵AB=CD,
∴HF=HE,
∴∠HFE=∠HEF,
∵HF∥AB,HE∥CD,
∴∠HFE=∠ONM,∠HEF=∠OMN,
∴∠ONM=∠OMN,
∴OM=ON,
∴△OMN是等腰三角形.
(2)如图,连接BD,取BD的中点H,连接HE,HF,
∴HF∥CN,HE∥BM,,,
∵AB=CD,
∴HF=HE,
∴∠HEF=∠HFE,
∵HF∥CN,HE∥BM,
∴∠HEF=∠BME,∠HFE=∠CNE,
∴∠BME=∠CNE.
【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
