4.2相似三角形
图片预览






文档简介
课件25张PPT。黄山松天坛非洲象中国地图 我们刚才所见到的图形有什么 相同和不同的地方?相同点: 形状相同.
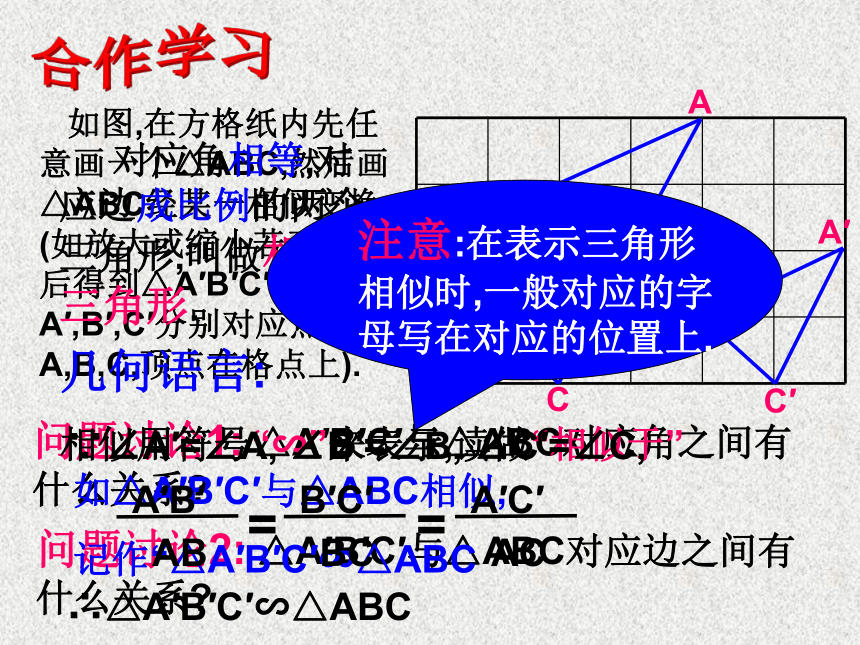
不同点: 大小不同. 生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为:相似图形知识回顾相似变换的性质: 图形的相似变换不改变图形中每一个角的大小;图形中的每条线段都扩大(或缩小)相同的倍数.4.2相似三角形 如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(点A′,B′,C′分别对应点A,B,C,顶点在格点上).问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?合作学习 对应角相等,对应边成比例的两个三角形,叫做相似三角形.相似用符号“∽”来表示,读做“相似于”如△A′B′C′与△ABC相似,
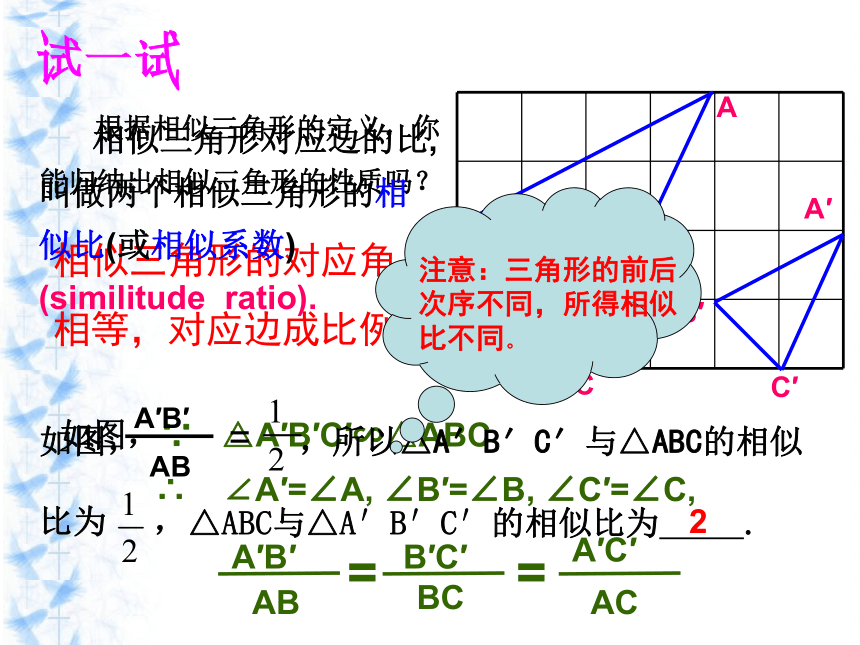
记作“△A′B′C′∽△ABC几何语言:∴△A′B′C′∽△ABC试一试 根据相似三角形的定义,你能归纳出相似三角形的性质吗?BAC相似三角形的对应角相等,对应边成比例.如图,∵ △A′B′C′∽△ABC∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C, 相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数) (similitude ratio).△ABC与△A′B′C′的相似比为 .2寻找相似三角形找朋友思考:当k=1时,这两个三角形又是什么关系呢? 形状相同,而且大小也相同 这样的三角形我们就称为全等三角形(congruent triangles). 全等三角形是相似三角形的特例 小练习: △ ABC与△ DEF相似,且相似比是0.75
则△ DEF 与△ ABC与的相似比是全等必相似,相似不一定全等两个全等三角形一定相似吗?为什么?两个等腰直角三角形呢?相似. 因为对应角相等, 对应边成比例 .两个等腰三角形不一定相似;
两个等边三角形一定相似.从上面的解答中,你获得了那些信息?两个直角三角形不一定相似.
因为对应角不一定相等,
对应边也不一定成比例;两个等腰三角形一定相似吗?为什么?两个等边三角形呢?两个等腰直角三角形相似。例1、如图,有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长度都是3.5cm。求该草坪其他两边的实际长度。解: 分析:它们的相似比2000:5= 400:1.如果设其它两边的实际长度都是xcm,那么X=3.5×400=1400(cm),
1400cm=14m.
所以,草坪其它两边的实际长度都是14m.益智的“模型”这是两个极具代表性的相似三角形基本模型: “A”型和“X” 型若△ADE∽ △ABC,则
∠DAE=∠BAC, ∠ADE=∠ A BC,
∠AED=∠ACB,若△ABC∽ △DEC,则
∠A=∠D, ∠B=∠E,
∠ACB=∠DCE,根据图形和条件分别说出两个三角形的对应角和对应边并写出比例式。对应角:∠A= ∠A
∠ADE= ∠B
∠AED= ∠C对应边:对应角:∠A= ∠A
∠ADB= ∠ABC
∠ABD= ∠C对应边:找一找点D和点B是对应点 已知:如图,AB∥EF ∥CD,则△AOB与_______和_______都相似。3图中共有____对相似三角形。 △EOF∽△COD△FOE△DOC AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC问题例1 已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.证明:∵D,E分别是AB,AC的中点,∴∠ADE=∠B,∠AED=∠C在△ADE和△ABC中,∠ADE=∠B,∠AED=∠C,∠A=∠A∴DE∥BC,DE= BC.∴△ADE∽△ABC例2:如图,D、E分别是△ABC的AB,AC边上的点, △ABC∽ △ADE.已知AD:DB=1:2,BC=9cm,求DE的长 例题讲解例2、如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED的大小;(2)求DE的长.
解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.1.如图,D是AB上的一点。 △ABC∽ △ACD ,且AD:AC=2:3,∠ADC= 65°, ∠B=43 °.
(1)求∠ABC, ∠ACD的度数;
(2)写出△ABC与 △ACD的对应边成比例的比例式,求出相似比。 2、如图,AB,CD相交于点0, △AOC∽ △BOD 。
(1)如果OC:OD=1:2,AC=5,求BD的长;
(2)如果∠A=35°, ∠AOC=100°,求∠D的度数。1、在下面的两组图形中,各有两个相似三角形,试确定x ,y ,m ,n 的值. X=32,y=20/3,m=800,n=550.m°50°45°2ay(2)CDEF 随堂练习 该出手时, 就出手△ABC与△DEF相似,就记作:△ABC∽△DEF注意:要把表示对应角顶点的字母写在对应的位置上!性质:相似三角形的各对应角相等,各对应边对应成比例.∠A = ∠D,∠B = ∠E,∠C = ∠F.三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形(similar trianglec).
D△ ABC∽ △DEF△ ABO∽ △CDO平行于三角形一边的直线和其他两边
(或两边的延长线)相交,所构成的
三角形与原三角形相似。预备定理
已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的最大边为8,求其余两边.已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.探究活动4,64,6或12,16或16/3,32/3对应角相等对应边成比例——“∽”k≠1 两个形状相同,大小不等的相似三角形k=1 两个全等三角形,是相似三角形的特例相似三角形定义相似比
(对应边的比值)
表示法一、基本知识: 1、寻找对应边的方法2、利用相似三角形的性质求角度或者线段长。 边的大小对应角的对边二、基本方法:(数形结合、分类讨论)收 获
不同点: 大小不同. 生活中我们会碰到许多这样形状相同的.大小不一定相同的图形,在数学上,我们把具有相同形状的图形称为:相似图形知识回顾相似变换的性质: 图形的相似变换不改变图形中每一个角的大小;图形中的每条线段都扩大(或缩小)相同的倍数.4.2相似三角形 如图,在方格纸内先任意画一个△ABC,然后画△ABC经某一相似变换(如放大或缩小若干倍)后得到△A′B′C′(点A′,B′,C′分别对应点A,B,C,顶点在格点上).问题讨论1: △A′B′C′与△ABC对应角之间有什么关系?问题讨论2: △A′B′C′与△ABC对应边之间有什么关系?合作学习 对应角相等,对应边成比例的两个三角形,叫做相似三角形.相似用符号“∽”来表示,读做“相似于”如△A′B′C′与△ABC相似,
记作“△A′B′C′∽△ABC几何语言:∴△A′B′C′∽△ABC试一试 根据相似三角形的定义,你能归纳出相似三角形的性质吗?BAC相似三角形的对应角相等,对应边成比例.如图,∵ △A′B′C′∽△ABC∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C, 相似三角形对应边的比,叫做两个相似三角形的相似比(或相似系数) (similitude ratio).△ABC与△A′B′C′的相似比为 .2寻找相似三角形找朋友思考:当k=1时,这两个三角形又是什么关系呢? 形状相同,而且大小也相同 这样的三角形我们就称为全等三角形(congruent triangles). 全等三角形是相似三角形的特例 小练习: △ ABC与△ DEF相似,且相似比是0.75
则△ DEF 与△ ABC与的相似比是全等必相似,相似不一定全等两个全等三角形一定相似吗?为什么?两个等腰直角三角形呢?相似. 因为对应角相等, 对应边成比例 .两个等腰三角形不一定相似;
两个等边三角形一定相似.从上面的解答中,你获得了那些信息?两个直角三角形不一定相似.
因为对应角不一定相等,
对应边也不一定成比例;两个等腰三角形一定相似吗?为什么?两个等边三角形呢?两个等腰直角三角形相似。例1、如图,有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长度都是3.5cm。求该草坪其他两边的实际长度。解: 分析:它们的相似比2000:5= 400:1.如果设其它两边的实际长度都是xcm,那么X=3.5×400=1400(cm),
1400cm=14m.
所以,草坪其它两边的实际长度都是14m.益智的“模型”这是两个极具代表性的相似三角形基本模型: “A”型和“X” 型若△ADE∽ △ABC,则
∠DAE=∠BAC, ∠ADE=∠ A BC,
∠AED=∠ACB,若△ABC∽ △DEC,则
∠A=∠D, ∠B=∠E,
∠ACB=∠DCE,根据图形和条件分别说出两个三角形的对应角和对应边并写出比例式。对应角:∠A= ∠A
∠ADE= ∠B
∠AED= ∠C对应边:对应角:∠A= ∠A
∠ADB= ∠ABC
∠ABD= ∠C对应边:找一找点D和点B是对应点 已知:如图,AB∥EF ∥CD,则△AOB与_______和_______都相似。3图中共有____对相似三角形。 △EOF∽△COD△FOE△DOC AB∥EF △AOB∽ △FOE AB∥CDEF∥CD△AOB ∽△DOC问题例1 已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.证明:∵D,E分别是AB,AC的中点,∴∠ADE=∠B,∠AED=∠C在△ADE和△ABC中,∠ADE=∠B,∠AED=∠C,∠A=∠A∴DE∥BC,DE= BC.∴△ADE∽△ABC例2:如图,D、E分别是△ABC的AB,AC边上的点, △ABC∽ △ADE.已知AD:DB=1:2,BC=9cm,求DE的长 例题讲解例2、如图,已知DE ∥ BC,AE=50cm,EC=30cm,BC=70cm,
∠BAC=450,∠ACB=400.
(1)求∠AED的大小;(2)求DE的长.
解: (1)DE ∥ BC△ADE∽△ABC∠AED=∠C=400.1.如图,D是AB上的一点。 △ABC∽ △ACD ,且AD:AC=2:3,∠ADC= 65°, ∠B=43 °.
(1)求∠ABC, ∠ACD的度数;
(2)写出△ABC与 △ACD的对应边成比例的比例式,求出相似比。 2、如图,AB,CD相交于点0, △AOC∽ △BOD 。
(1)如果OC:OD=1:2,AC=5,求BD的长;
(2)如果∠A=35°, ∠AOC=100°,求∠D的度数。1、在下面的两组图形中,各有两个相似三角形,试确定x ,y ,m ,n 的值. X=32,y=20/3,m=800,n=550.m°50°45°2ay(2)CDEF 随堂练习 该出手时, 就出手△ABC与△DEF相似,就记作:△ABC∽△DEF注意:要把表示对应角顶点的字母写在对应的位置上!性质:相似三角形的各对应角相等,各对应边对应成比例.∠A = ∠D,∠B = ∠E,∠C = ∠F.三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形(similar trianglec).
D△ ABC∽ △DEF△ ABO∽ △CDO平行于三角形一边的直线和其他两边
(或两边的延长线)相交,所构成的
三角形与原三角形相似。预备定理
已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的最大边为8,求其余两边.已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.探究活动4,64,6或12,16或16/3,32/3对应角相等对应边成比例——“∽”k≠1 两个形状相同,大小不等的相似三角形k=1 两个全等三角形,是相似三角形的特例相似三角形定义相似比
(对应边的比值)
表示法一、基本知识: 1、寻找对应边的方法2、利用相似三角形的性质求角度或者线段长。 边的大小对应角的对边二、基本方法:(数形结合、分类讨论)收 获
同课章节目录
