4.4.2 相似三角形的性质及应用

课件17张PPT。4.4相似三角形的性质及其应用(2)浙教版九年级《数学》上册复习提问我们已经学习相似三角形的性质有哪些？1、相似三角形对应角相等。2、相似三角形对应边成比例。 3、相似三角形的周长之比等于相似比；∵⊿A′B′C′∽⊿ABC ∴ ∠A= ∠A′，∠B= ∠B′
∠C= ∠C′∵⊿ABC∽⊿ABC ∴AB：A′B′=BC ：B′C′=CA ：C′A′4、相似三角形的面积之比等于相似比的平方。5、相似三角形对应边上的高线之比、对应边上中线之比、
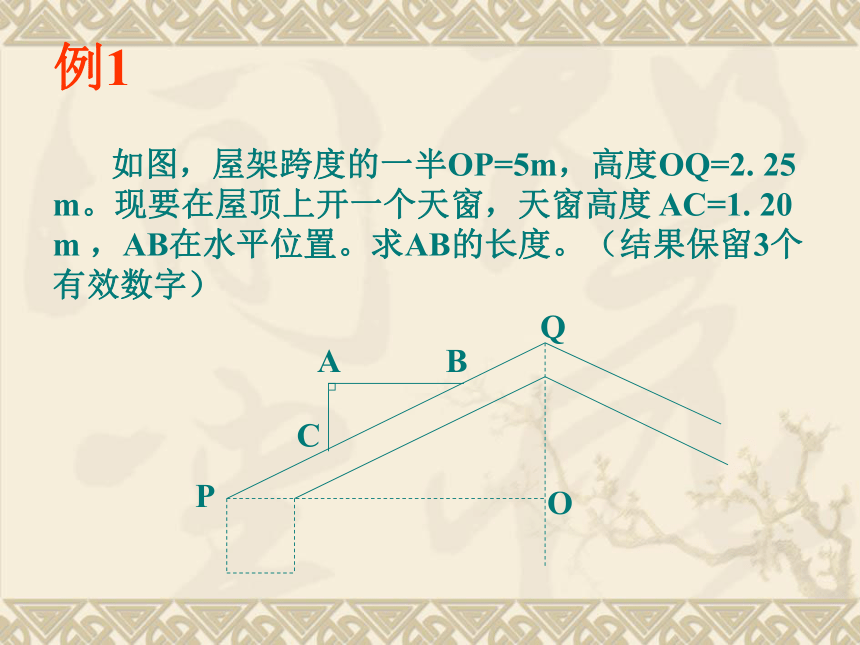
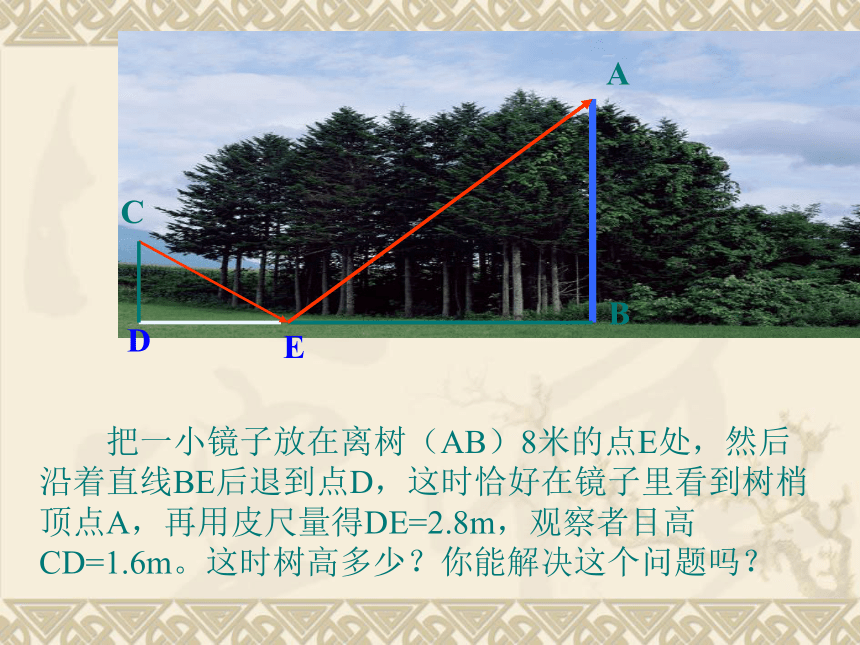
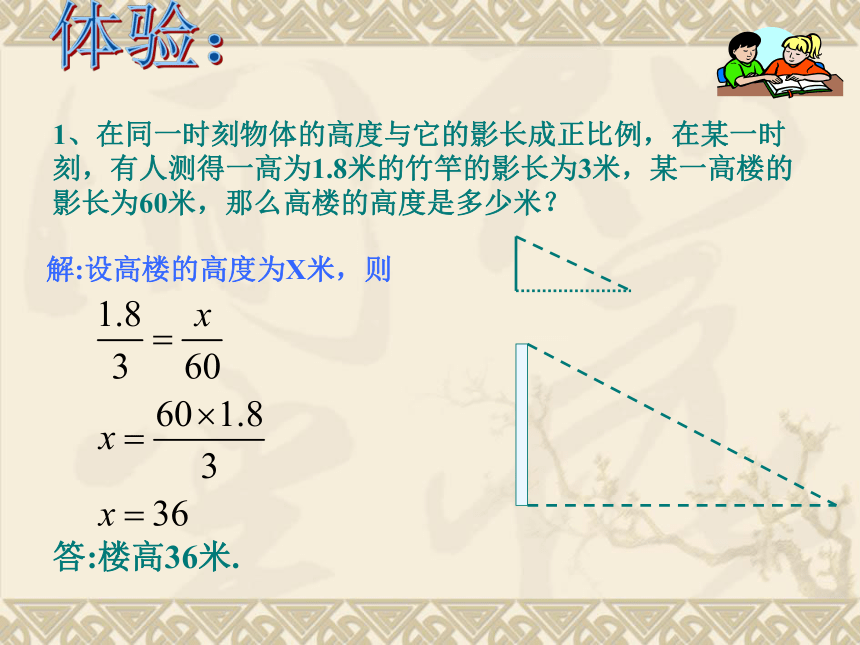
对应角平分线之比等于相似比.例1 如图，屋架跨度的一半OP=5m，高度OQ=2. 25 m。现要在屋顶上开一个天窗，天窗高度 AC=1. 20 m ，AB在水平位置。求AB的长度。（结果保留3个有效数字）例2要测量树的高度，你有什么方法？ 把一小镜子放在离树（AB）8米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.8m，观察者目高CD=1.6m。这时树高多少？你能解决这个问题吗？ABEDC 把长为2.40m的标杆CD直立在地面上，量出树的影长为2.80m，标杆的影长为1.47m。这时树高多少？你能解决这个问题吗？ ABCD1、在同一时刻物体的高度与它的影长成正比例，在某一时刻，有人测得一高为1.8米的竹竿的影长为3米，某一高楼的影长为60米，那么高楼的高度是多少米？解:设高楼的高度为X米，则答:楼高36米.体验：课内练习： 步枪在瞄准时的示意图如图，从眼睛到准星的距离OE为80cm，步枪上准星宽度AB为2mm，目标的正面宽度CD为50cm，求眼睛到目标的距离OF。反馈与评价2.如图:小明在打网球时,要使球恰好能打过网 ,而且落在离网５米的位置上，则拍击球的高度应为（　　） 。A、2.7米 B、1.8米 C、0.9米 D、 6米 Ａ1.铁道的栏杆的短臂为OA=1米，
长臂OB=10米，短臂端下降
AC=0.6米，则长臂端上升BD= 米。1M10M0.6M6 2.如图，△ABC是一块锐角三角形余料，边BC=120毫米，高AD=80毫米，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？NMQPEDCBA解：设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC，所以△APN∽ △ABC
所以3.如图，已知零件的外径为a，要求它的厚度x，需先求出内孔的直径AB，现用一个交叉卡钳（两条尺长AC和BD相等）去量，若OA:OC=OB:OD=n，且量得CD=b，求厚度x。O（分析：如图，要想求厚度x，根据条件可知，首先得求出内孔直径AB。而在图中可构造出相似形，通过相似形的性质，从而求出AB的长度。）O课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解解决实际问题时（如测高、测距），
一般有以下步骤：①审题 ②构建图形
③利用相似解决问题怎样利用相似三角形的有关知识测量旗杆的高度?想一想怎样测量旗杆的高度呢？求旗杆高度的方法:
旗杆的高度和影长组成的三角形人身高和影长组成的三角形因为旗杆的高度不能直接测量,我们可以利用再利用相似三角形对应边成比例来求解.
相似于结束寄语不经历风雨，怎么见彩虹.,没有人能随随便便成功!