2025.4宁波中学大讲堂测试卷(含答案)
文档属性
| 名称 | 2025.4宁波中学大讲堂测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 104.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-30 00:00:00 | ||
图片预览




文档简介
2025.4 宁波中学大讲堂测试
一. 单选题(每题 5 分,共 20 分)
1. 已知关于 的方程 有三个互不相等的正整数解,则 的值为 ( )
A. -6 B. -7 C. 7 D. 6
2. 下列说法:
①已知 满足 ,则 ;
②已知 是正整数, ,且 ,则 ;
③若实数 满足 ,则代数式 的值可以是 6. 其中正确的个数是 ( )
A. 0 B. 1 C. 2 D. 3
3. 二次函数 的图象如图所示,顶点的横坐标为 2, 点 和点 均在该函数的图象上,则下列说法正确的是 ( )
A.
B. 若 ,则
C. 当 时,
D. 若函数图象与 轴的一个交点的横坐标为 -1,则当 或 时,
4. 如图,在 中, 动点 从点 开始以 的速度沿 边向点 运动;动点 从点 开始以 的速度沿 边向点 运动. 如果 两点分别从 两点同时出发,设运动时间为 秒.
①当 时, 的面积为 ;
② 有两个不同的值,都使 的面积为 ;
③ 面积的最大值为 . 其中,正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
二. 填空题 (每题 5 分, 共 20 分)
5. 多项式 可分解为_____.
6. 当正整数 _____时,分式 的值也是正整数.
7. 若实数 满足条件 , 则 的值是_____.
8. 已知方程 有两个质数解,则 _____.
三. 解答题(每题 15 分,共 60 分)
9. (1) 因式分解: ;
设 表示不超过 的最大整数(例如:[2] ),求方程 的解.
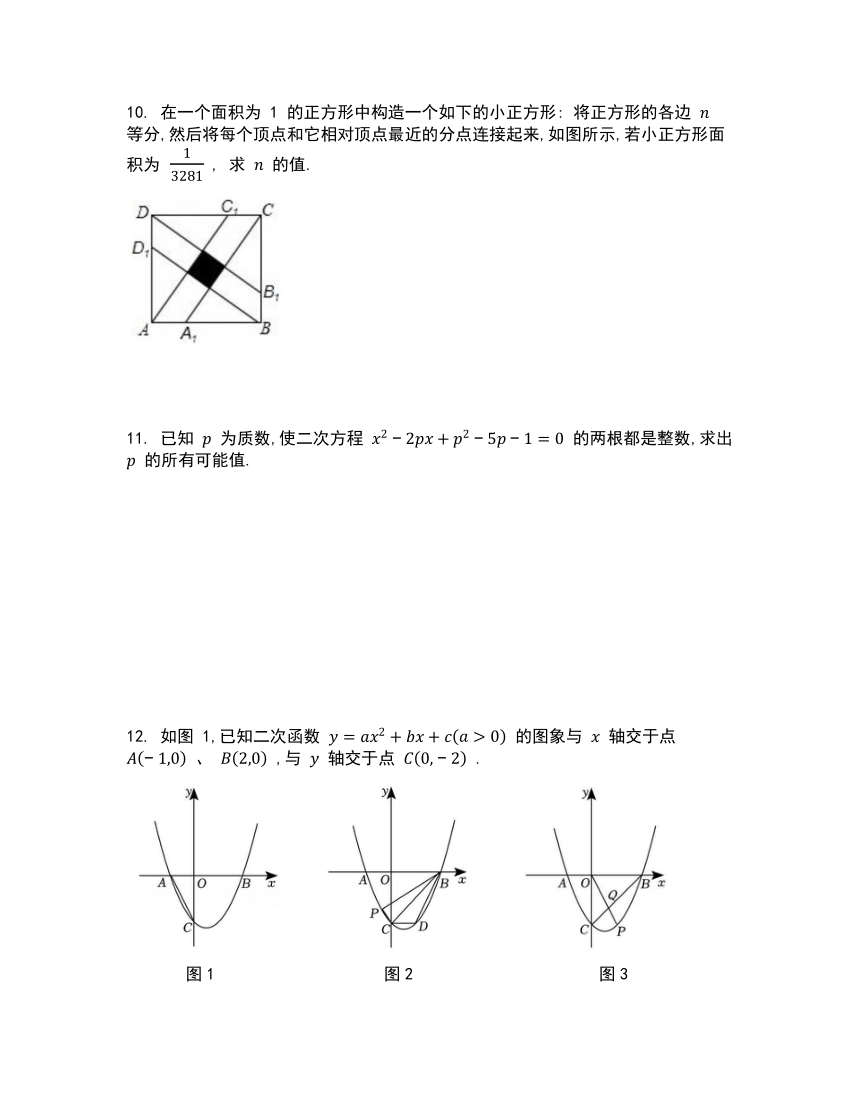
10. 在一个面积为 1 的正方形中构造一个如下的小正方形: 将正方形的各边 等分,然后将每个顶点和它相对顶点最近的分点连接起来,如图所示,若小正方形面积为 , 求 的值.
已知 为质数,使二次方程 的两根都是整数,求出 的所有可能值.
如图 1,已知二次函数 的图象与 轴交于点 、 ,与 轴交于点 .
图1 图2 图3
(1)求二次函数的解析式;
(2)如图 2,过点 作 轴交二次函数图象于点 , 是二次函数图象上异于点 的一个动点,连结 ,若 ,求点 的坐标;
(3)如图 3,若点 是二次函数图象上位于 下方的一个动点,连结 交 于点 . 是否存在点 使 的值最大. 若存在请求出 的最大值; 若不存在请说明理由.
参考答案解析
一. 单选题 (每题 5 分, 共 20 分)
1. 【解答】解: 三次方程 的三个根是 ,
则 ,
方程 三个根 ,
又 为三个互不相等的正整数,
,
,
故选: A.
2. 【解答】解: ① ,
,
;
故①是正确的;
② ,
是正整数,
,
,
或 ,
或 ,
或 ,
故②是错误的;
③由题意得: ,
若 的值可以是 6,
则: ,
则: 为方程 的解,
,
不存在实数 ,
故③是错误的;
故选: B.
3. 【解答】解: 二次函数 的顶点的横坐标为 2,
,
,故 不正确;
函数开口向下,
离对称轴越远函数值越小,
对称轴为直线 ,
,故 不正确;
二次函数 的开口向下,顶点的横坐标为 2,
时,函数有最大值 ,
当 时, ,即当 时, ,故 正确;
函数图象与 轴的一个交点的横坐标为 -1,对称轴为直线 ,
函数图象与 轴的另一个交点的横坐标为 5,
由图可知: 当 或 时, ,故 不正确;
故选: .
4. 【解答】解: 由题意得: ,
,
,
,
,
当 时, 的面积有最大值为 25,故③错误;
当 时, 的面积为: ,故①正确;
令 ,则 ,即 ,
解得 或 8,
时, ,故 符合题意,故②正确;
故选: .
二. 填空题 (每题 5 分, 共 20 分)
5. 【解答】解: ,
,
,
.
【解答】解: 原式
分式 的值是正整数, 也是正整数,
是整数,
,
解得 或 或 或 (舍去),
当 时,分式 (不符合题意舍去),
故答案为: 2 或 8 .
7. 【解答】解: 将题中等式移项并将等号两边同乘以 4 得 ,
且 且
,
.
故答案为:14.
8. 【解答】解: 设方程 的两根分别为 ,
由一元二次方程根与系数的关系得, ,
是奇数,
又 、 是质数,
必有一个等于 2,
设 ,则 ,
,
.
故答案为: 3994.
三. 解答题(每题 15 分,共 60 分)
9. 【解答】
(1)解: 原式
.
(2)解: 令 ,代入原方程得 ,即 ,
又 ,
,
整理得: ,即 ,
或 或 ,
当 时, ,
当 时, ,
当 时, ,
经检验, 或 或 是原方程的解.
故答案为:-4或 或 .
10. 【解答】解: ,
过 作 于 ,则 ,
得 .
,
得 ,故 (舍去).
故答案为:41 .
11. 【解答】解: 已知的整系数二次方程有整数根,
为完全平方数,
从而, 为完全平方数
设 ,注意到 ,故 ,且 为整数
,
则 中至少有一个是 5 的倍数,即 为正整数)
由 是质数, ,
或 7
当 时,已知方程变为 ,解得 ;
当 时,已知方程变为 ,解得
所以 或 .
12. 【解答】解: (1) 设二次函数的解析式为: ,
将 代入得: ,
解得: ,
;
(2) 如图 2:
当点 在直线 的上方时,
过点 作 轴,交 的延长线于点 ,
设直线 的解析式为 ,
将 代入得:
解得:
直线 的解析式为 ,
设点 ,则点 ,
二次函数 的图象与 轴交于点 、 ,
对称轴为 ,
,
即 ,
则 ,
,
即 ,
解得: ,
当 时, ,
当 时, ,
或 ;
当点 在 的下方时,
同理得出 ,
,
,
此时点 和点 重合,故舍去,
或 ;
(3) 如图3:
设 作 于 ,交 于 ,
,
,
,
,
,
当 时, 的最大值为 .
一. 单选题(每题 5 分,共 20 分)
1. 已知关于 的方程 有三个互不相等的正整数解,则 的值为 ( )
A. -6 B. -7 C. 7 D. 6
2. 下列说法:
①已知 满足 ,则 ;
②已知 是正整数, ,且 ,则 ;
③若实数 满足 ,则代数式 的值可以是 6. 其中正确的个数是 ( )
A. 0 B. 1 C. 2 D. 3
3. 二次函数 的图象如图所示,顶点的横坐标为 2, 点 和点 均在该函数的图象上,则下列说法正确的是 ( )
A.
B. 若 ,则
C. 当 时,
D. 若函数图象与 轴的一个交点的横坐标为 -1,则当 或 时,
4. 如图,在 中, 动点 从点 开始以 的速度沿 边向点 运动;动点 从点 开始以 的速度沿 边向点 运动. 如果 两点分别从 两点同时出发,设运动时间为 秒.
①当 时, 的面积为 ;
② 有两个不同的值,都使 的面积为 ;
③ 面积的最大值为 . 其中,正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
二. 填空题 (每题 5 分, 共 20 分)
5. 多项式 可分解为_____.
6. 当正整数 _____时,分式 的值也是正整数.
7. 若实数 满足条件 , 则 的值是_____.
8. 已知方程 有两个质数解,则 _____.
三. 解答题(每题 15 分,共 60 分)
9. (1) 因式分解: ;
设 表示不超过 的最大整数(例如:[2] ),求方程 的解.
10. 在一个面积为 1 的正方形中构造一个如下的小正方形: 将正方形的各边 等分,然后将每个顶点和它相对顶点最近的分点连接起来,如图所示,若小正方形面积为 , 求 的值.
已知 为质数,使二次方程 的两根都是整数,求出 的所有可能值.
如图 1,已知二次函数 的图象与 轴交于点 、 ,与 轴交于点 .
图1 图2 图3
(1)求二次函数的解析式;
(2)如图 2,过点 作 轴交二次函数图象于点 , 是二次函数图象上异于点 的一个动点,连结 ,若 ,求点 的坐标;
(3)如图 3,若点 是二次函数图象上位于 下方的一个动点,连结 交 于点 . 是否存在点 使 的值最大. 若存在请求出 的最大值; 若不存在请说明理由.
参考答案解析
一. 单选题 (每题 5 分, 共 20 分)
1. 【解答】解: 三次方程 的三个根是 ,
则 ,
方程 三个根 ,
又 为三个互不相等的正整数,
,
,
故选: A.
2. 【解答】解: ① ,
,
;
故①是正确的;
② ,
是正整数,
,
,
或 ,
或 ,
或 ,
故②是错误的;
③由题意得: ,
若 的值可以是 6,
则: ,
则: 为方程 的解,
,
不存在实数 ,
故③是错误的;
故选: B.
3. 【解答】解: 二次函数 的顶点的横坐标为 2,
,
,故 不正确;
函数开口向下,
离对称轴越远函数值越小,
对称轴为直线 ,
,故 不正确;
二次函数 的开口向下,顶点的横坐标为 2,
时,函数有最大值 ,
当 时, ,即当 时, ,故 正确;
函数图象与 轴的一个交点的横坐标为 -1,对称轴为直线 ,
函数图象与 轴的另一个交点的横坐标为 5,
由图可知: 当 或 时, ,故 不正确;
故选: .
4. 【解答】解: 由题意得: ,
,
,
,
,
当 时, 的面积有最大值为 25,故③错误;
当 时, 的面积为: ,故①正确;
令 ,则 ,即 ,
解得 或 8,
时, ,故 符合题意,故②正确;
故选: .
二. 填空题 (每题 5 分, 共 20 分)
5. 【解答】解: ,
,
,
.
【解答】解: 原式
分式 的值是正整数, 也是正整数,
是整数,
,
解得 或 或 或 (舍去),
当 时,分式 (不符合题意舍去),
故答案为: 2 或 8 .
7. 【解答】解: 将题中等式移项并将等号两边同乘以 4 得 ,
且 且
,
.
故答案为:14.
8. 【解答】解: 设方程 的两根分别为 ,
由一元二次方程根与系数的关系得, ,
是奇数,
又 、 是质数,
必有一个等于 2,
设 ,则 ,
,
.
故答案为: 3994.
三. 解答题(每题 15 分,共 60 分)
9. 【解答】
(1)解: 原式
.
(2)解: 令 ,代入原方程得 ,即 ,
又 ,
,
整理得: ,即 ,
或 或 ,
当 时, ,
当 时, ,
当 时, ,
经检验, 或 或 是原方程的解.
故答案为:-4或 或 .
10. 【解答】解: ,
过 作 于 ,则 ,
得 .
,
得 ,故 (舍去).
故答案为:41 .
11. 【解答】解: 已知的整系数二次方程有整数根,
为完全平方数,
从而, 为完全平方数
设 ,注意到 ,故 ,且 为整数
,
则 中至少有一个是 5 的倍数,即 为正整数)
由 是质数, ,
或 7
当 时,已知方程变为 ,解得 ;
当 时,已知方程变为 ,解得
所以 或 .
12. 【解答】解: (1) 设二次函数的解析式为: ,
将 代入得: ,
解得: ,
;
(2) 如图 2:
当点 在直线 的上方时,
过点 作 轴,交 的延长线于点 ,
设直线 的解析式为 ,
将 代入得:
解得:
直线 的解析式为 ,
设点 ,则点 ,
二次函数 的图象与 轴交于点 、 ,
对称轴为 ,
,
即 ,
则 ,
,
即 ,
解得: ,
当 时, ,
当 时, ,
或 ;
当点 在 的下方时,
同理得出 ,
,
,
此时点 和点 重合,故舍去,
或 ;
(3) 如图3:
设 作 于 ,交 于 ,
,
,
,
,
,
当 时, 的最大值为 .
同课章节目录
