4.5 相似多边形

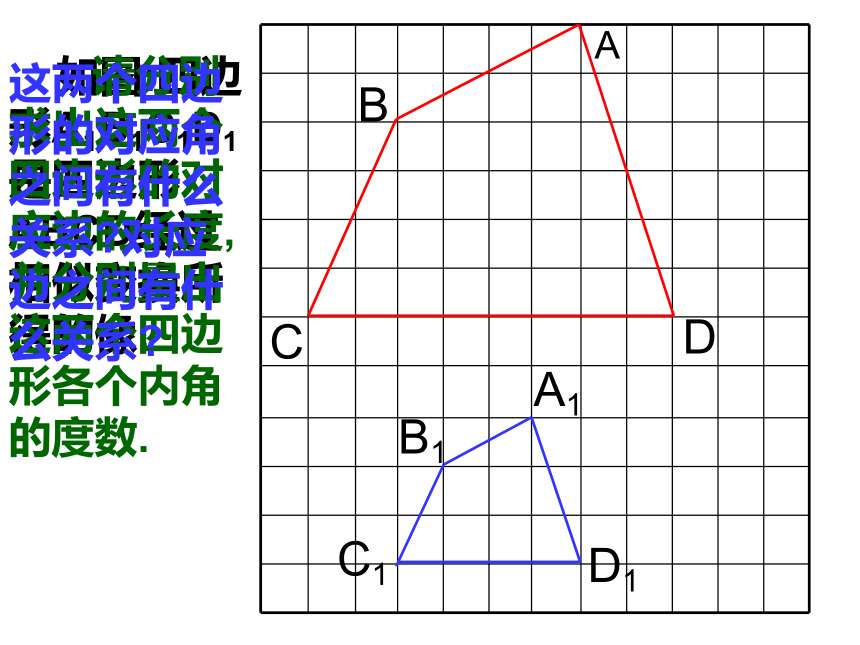
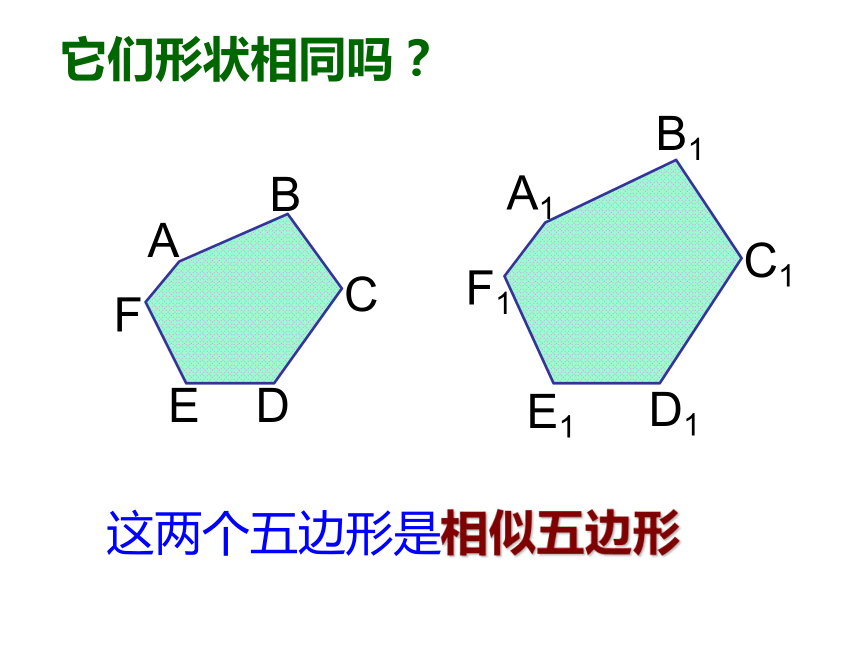
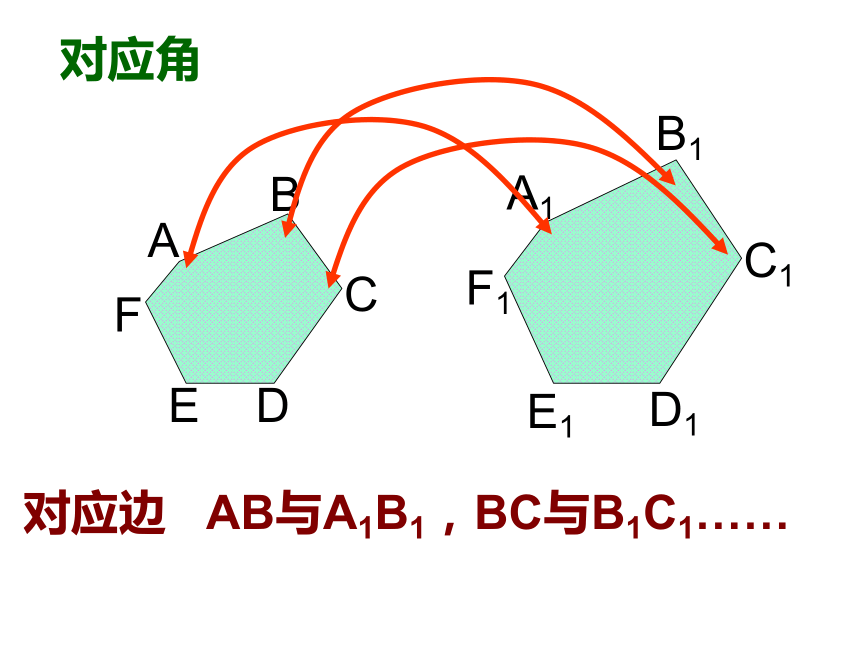
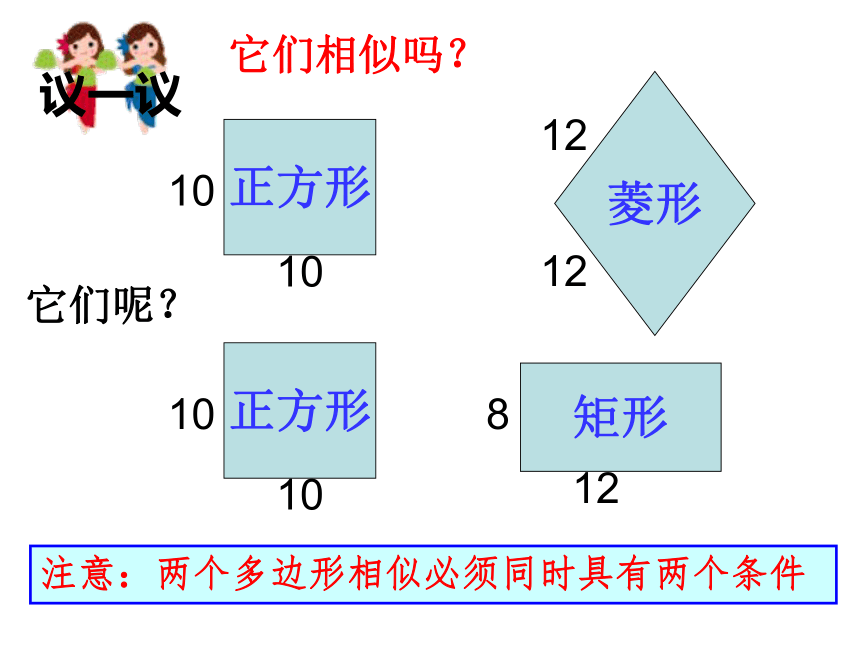
课件18张PPT。4.5相似多边形ABCDA1B1C1D1 如图:四边形A1B1C1D1是四边形ABCD经过相似变换所得的像. 请分别求出这两个四边形的对应边的长度,并分别量出这两个四边形各个内角的度数.这两个四边形的对应角之间有什么关系?对应边之间有什么关系? 各角对应相等、各边对应成比例的两个多边形叫做相似多边形.对应顶点的字母写在对应的位置上定义ABCDEFA1B1C1D1E1F1它们形状相同吗？这两个五边形是相似五边形对应角对应边 AB与A1B1，BC与B1C1……它们相似吗？它们呢？注意：两个多边形相似必须同时具有两个条件(1)两个大小不等的矩形是相似的(×)(2)一个正方形与一个平行四边形相似(3)所有的正六边形都相似(4)两个大小不等的菱形相似(5)各角对应相等菱形都是相似形(6)顺次连结矩形各边中点所得四边形与原四边形相似(7)顺次连结菱形各边中点所得四边形与原四边形相似(×)(√) (×)(√)(×)(×)1.判断对错并说明理由:例题解:两个矩形纸张相似.理由如下:设原来的纸张为矩形ABCD,对折线EF把矩形ABCD分为两个全等的矩形.在矩形ABFE中∴两个矩形的对应角相等,对应边成比例,∴矩形ABFE与矩形BCDA相似.试一试： 下列每组图形的形状相同，它们的对应角有怎样的关系?对应边呢？
(1) 正三角形ABC与正三角形DEF;
(2) 正方形ABCD与正方形EFGH.解:(1)由于正三角形每个角等于60°，所以∠A=∠D= 60°, ∠B=∠E=60°, ∠C=∠F= 60° .由于正三角形三边相等，所以
AB:DE=BC:EF=CA:FD所有的正三角形都是相似多边形做一做 2正方形ABCD与正方形EFGH 是相似多边形吗?∴正方形ABCD与正方形EFGH 是相似多边形.解：由于正方形的每个角都是直角，所以 ∠A=∠E= 90° ∠B=∠F=90°∠C=∠G= 90° ∠D=∠H= 90°由于正方形的四边相等，所以AB:EF=BC:FG=CD:GH=DA:HE2∶3相似.理由是：各对应角相等，各对应边成比例2、如图，两个正六边形的边长分别为a和b，它们相似吗？为什么？1、右面两个矩形相似，求它们对应边的比.练一练做一做3.一块长为3m，宽为1.5m的矩形黑板如图所示，镶在其外围的木质边框7.5cm,边框的内外边缘所成的矩形相似吗？答：不相似。因为内部的矩形的长为 300cm,宽为150cm；外部矩形的长为315cm，宽为165cm300：315≠150：165
所以两矩形不相似。1、如图:四边形A1B1 C1D1与四边形ABCD相似,相似比是k,求这两个四边形的周长比.2、（1）连结第一题图两个相似四边形的对角线BD，B1D1，所得的△CBD和△C1B1D1相似么？另外的一对三角形是否也相似呢？相似比是多少？（2）这两个四边形
的面积之比与相似比有什么关系？做一做相似多边形的周长之比等于相似比相似多边形的面积之比等于相似比的平方. 如果两个多边形相似，那么它们的对应角有什么关系？对应边呢？ 相似多边形的对应角相等，对应边成比例.相似多边形的性质相似多边形的周长之比等于相似比;面积之比等于相似比的平方.1、如图，矩形ABCD∽矩形BCFE，且AD=AE，求AB：AD的值练一练2、在如图所示的相似四边形中，求未知的边长x和角度α的大小可以发现，这些叠放起来的矩形的右上顶点同在一直线上，这是因为这些小矩形都是相似的，所以它们的长与宽对应成比例，（１）（２）如果以图（１）最大矩形的左下顶点为原点，宽和长所在直线分别为x轴、y轴，那么这组矩形右上顶点的坐标都满足把标准纸（长与宽之比为　）一次又一次对开如右图叠起来，你发现了什么有趣的现象？你能给出数学解释吗？　　　　探究活动相似多边形小结 1.各对应角相等、各对应边成比例的两个多边形叫做相似多边形. 3.相似多边形对应边的比叫做相似比. 2.对应顶点的字母写在对应的位置上. 相似多边形的对应角相等，对应边成比例.4相似多边形的性质 相似多边形的周长之比等于相似比;面积之比等于相似比的平方.1.作业本 2.《同步》回家作业