第五章特殊平行四边形单元测试卷(一)(含答案)
文档属性
| 名称 | 第五章特殊平行四边形单元测试卷(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 18:24:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章特殊平行四边形单元测试卷(一)浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
2.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
3.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG的值为( )
A. B. C. D.
4.用一条长为40cm的绳子围成一个面积为a cm2的长方形,a的值不可能为( )
A.20 B.100 C.40 D.160
5.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形
B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形
D.若CH=3,CG=4,则CE=2.5
6.如图,边长为4cm的正方形ABCD的对角线相交于点O,点O又是正方形EFGO的一个顶点,则两个正方形重叠部分的面积是( )cm2.
A.8 B.4 C.6 D.2
7.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.1.2 B.1.3 C.1.4 D.2.4
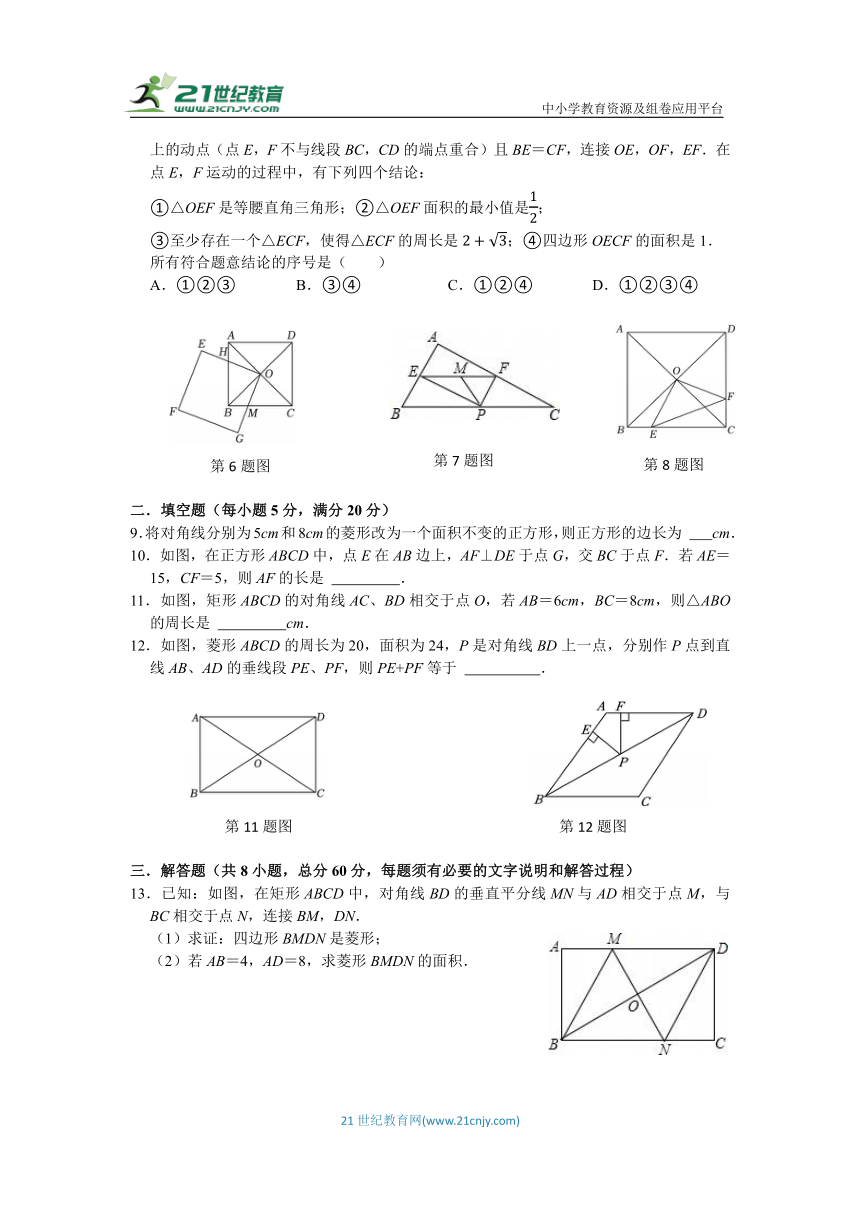
8.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;②△OEF面积的最小值是;
③至少存在一个△ECF,使得△ECF的周长是;④四边形OECF的面积是1.
所有符合题意结论的序号是( )
A.①②③ B.③④ C.①②④ D.①②③④
二.填空题(每小题5分,满分20分)
9.将对角线分别为5cm和8cm的菱形改为一个面积不变的正方形,则正方形的边长为 cm.
10.如图,在正方形ABCD中,点E在AB边上,AF⊥DE于点G,交BC于点F.若AE=15,CF=5,则AF的长是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,若AB=6cm,BC=8cm,则△ABO的周长是 cm.
12.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的面积.
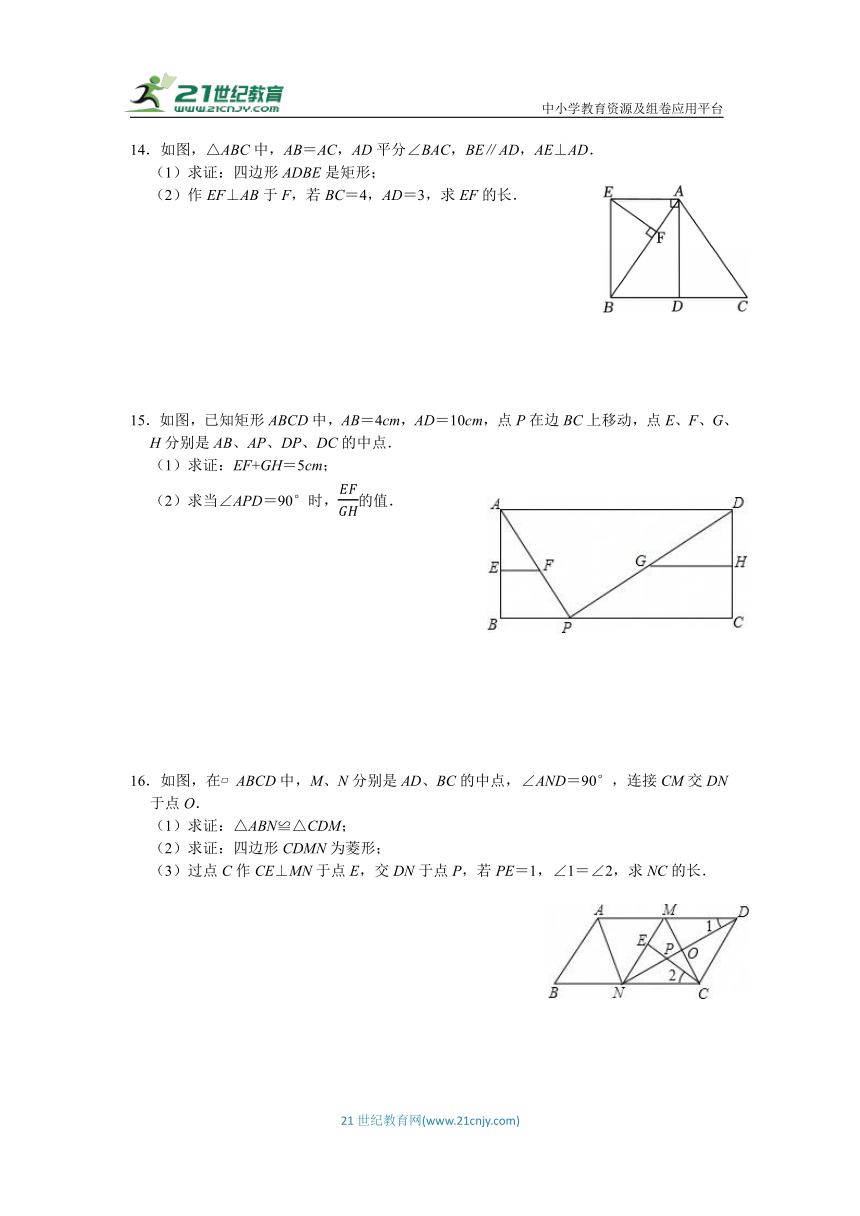
14.如图,△ABC中,AB=AC,AD平分∠BAC,BE∥AD,AE⊥AD.
(1)求证:四边形ADBE是矩形;
(2)作EF⊥AB于F,若BC=4,AD=3,求EF的长.
15.如图,已知矩形ABCD中,AB=4cm,AD=10cm,点P在边BC上移动,点E、F、G、H分别是AB、AP、DP、DC的中点.
(1)求证:EF+GH=5cm;
(2)求当∠APD=90°时,的值.
16.如图,在 ABCD中,M、N分别是AD、BC的中点,∠AND=90°,连接CM交DN于点O.
(1)求证:△ABN≌△CDM;
(2)求证:四边形CDMN为菱形;
(3)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求NC的长.
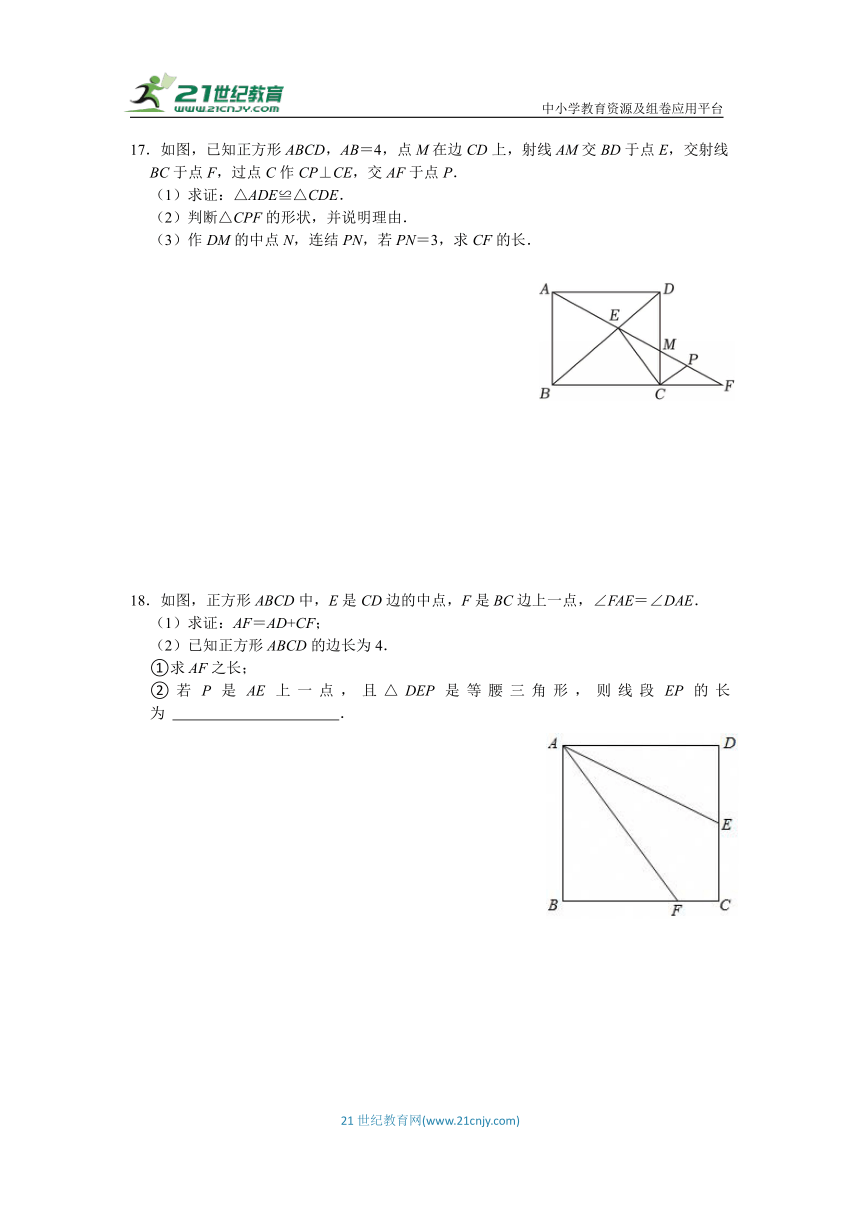
17.如图,已知正方形ABCD,AB=4,点M在边CD上,射线AM交BD于点E,交射线BC于点F,过点C作CP⊥CE,交AF于点P.
(1)求证:△ADE≌△CDE.
(2)判断△CPF的形状,并说明理由.
(3)作DM的中点N,连结PN,若PN=3,求CF的长.
18.如图,正方形ABCD中,E是CD边的中点,F是BC边上一点,∠FAE=∠DAE.
(1)求证:AF=AD+CF;
(2)已知正方形ABCD的边长为4.
①求AF之长;
②若P是AE上一点,且△DEP是等腰三角形,则线段EP的长为 .
参考答案
一、选择题
1—8:CDCDCBAD
二、填空题
9.【解答】解:∵菱形的对角线分别为5cm和8cm,
∴菱形的面积S5×8=20cm2,
∴正方形的边长是2(cm).
故答案为:2.
10.【解答】解:∵四边形ABCD是正方形,
∴AB=AD=BC,∠B=DAB=90°,
∴∠BAF+∠FAD=90°,
∵AF⊥DE,
∴∠FAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中,
,
∴△BAF≌△ADE(ASA),
∴BF=AE=15,
∵CF=5,
∴BC=BF+CF=20,
∴AB=BC=20,
在Rt△ABF中,AB=20,BF=15,
由勾股定理得:AF25.
故答案为:25.
11.【解答】解:在矩形ABCD中,对角线AC,BD相交于点O,AB=6cm,BC=8cm,
∴∠ABC=90°,OA=OBAC,
∴AC10(cm),
∴AO=BO=5cm,
∴△ABO的周长为OA+OB+AB=16(cm).
故答案为:16.
12.【解答】解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
∴S菱形BMDN=DM AB=5×4=20.
14.【解答】(1)证明:∵△ABC中,AB=AC,AD平分∠BAC,
∴AD⊥BC,∠ADB=90°,
∵BE∥AD,AE⊥AD,
∴∠DBE=90°,∠DAE=90°,
∴四边形ADBE是矩形;
(2)解:∵AB=AC,AD平分∠BAC,BC=4,AD=3,
∴.
在直角三角形ABD中,由勾股定理得:.
∵四边形ADBE是矩形,
∴BE=AD=3,AE=BD=2.
∵,
∴.
15.【解答】(1)证明:∵矩形ABCD,AD=10cm,
∴BC=AD=10cm.
∵E、F、G、H分别是AB、AP、DP、DC的中点,
∴EF+GHBPPCBC.
∴EF+GH=5cm.
(2)解:∵矩形ABCD,
∴∠B=∠C=90°,
又∵∠APD=90°,
在直角△APD中,AD2=AP2+DP2,
同理,AP2=AB2+BP2,PD2=PC2+CD2=PC2+AB2,
∴AD2=AP2+DP2=AB2+BP2+PC2+DC2=BP2+(BC﹣BP)2+2AB2=BP2+(10﹣BP)2+32,
即100=2BP2﹣20BP+100+32,
解得BP=2或8(cm),
当BP=2时,PC=8,EF=1,GH=4,这时,
当BP=8时,PC=2,EF=4,GH=1,这时,
∴的值为或4.
16.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,,
∴△ABN≌△CDM(SAS);
(2)证明:∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC∥DM,NC=DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形.
(3)解:∵M是AD的中点,∠AND=90°,
∴MN=MDAD,
∴∠1=∠MND,
∵AD∥BC,
∴∠1=∠CND,
∵∠1=∠2,
∴∠MND=∠CND=∠2,
∴PN=PC,
∵CE⊥MN,
∴∠CEN=90°,
∠END+∠CNP+∠2=180°﹣∠CEN=90°,
又∵∠END=∠CNP=∠2,
∴∠2=∠PNE=30°,
∵PE=1,
∴PN=2PE=2,
∴CE=PC+PE=3,
∴NC2.
17.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE=45°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS);
(2)解:△CPF是等腰三角形,理由如下:
∵△ADE≌△CDE,
∴∠DAE=∠DCE,
又∵CP⊥CE,DC⊥CF,
∴∠DCE=∠PCF,
又∵AD∥BF,
∴∠DAE=∠CFP,
∴∠PCF=∠PFC,
∴CP=PF,
∴△CPF是等腰三角形;
(3)解:如图,连接DF,
∵∠PCF=∠PFC,
∴∠PCM=∠PMC,
∴PC=MP,
∴MP=PF,
又∵点N是DM的中点,
∴DF=2NP=6,
∴CF2.
18.【解答】(1)证明:如图1,过E点作EG⊥AF,垂足为G,连接EF,
(也可延长AE、BC交于P,用全等和等腰三角形知识解决),
∵EG⊥AF,
∴∠EGF=∠AGE=90°,
∵四边形ABCD是正方形,
∴∠C=∠D=90°,
在△AGE和△ADE中,
∴△AGE≌△ADE(AAS),
∴AD=AG,GE=DE,
∵E是CD边的中点,
∴CE=DE,
∴GE=CE,
在Rt△EGF和Rt△ECF中,
∴Rt△EGF≌Rt△ECF(HL),
∴GF=CF,
∵AF=AG+GF,
∴AF=AD+CF;
(2)解:①设CF=x,则BF=4﹣x,AF=4+x,
在Rt△ABF中,AB2+BF2=AF2,
∴42+(4﹣x)2=(4+x)2,
解得:x=1,
∴AF=4+x=4+1=5;
②分三种情况:
i)如图2,PD=DE,过D作DG⊥AE于G,
∴EP=2EG,
Rt△ADE中,AD=4,DE=2,
∴AE2,
∴S△ADE,
即,
∴DG,
由勾股定理得:EG,
∴EP=2EG;
ii)如图3,EP=DE=2;
iii)如图4,PD=PE,过P作PM⊥DE于M,则DM=EM,
∵AD⊥CD,PM⊥DE,
∴AD∥PM,
∴AP=PE,
∵AE=2,
∴EP,
综上,EP的长是2或或.
21世纪教育网(www.21cnjy.com)
第五章特殊平行四边形单元测试卷(一)浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
2.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
3.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG的值为( )
A. B. C. D.
4.用一条长为40cm的绳子围成一个面积为a cm2的长方形,a的值不可能为( )
A.20 B.100 C.40 D.160
5.如图,D,E是△ABC中AB,BC边上的点,且DE∥AC,∠ACB角平分线和它的外角的平分线分别交DE于点G和H.则下列结论错误的是( )
A.若BG∥CH,则四边形BHCG为矩形
B.若BE=CE时,四边形BHCG为矩形
C.若HE=CE,则四边形BHCG为平行四边形
D.若CH=3,CG=4,则CE=2.5
6.如图,边长为4cm的正方形ABCD的对角线相交于点O,点O又是正方形EFGO的一个顶点,则两个正方形重叠部分的面积是( )cm2.
A.8 B.4 C.6 D.2
7.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.1.2 B.1.3 C.1.4 D.2.4
8.已知:如图,正方形ABCD中,AB=2,AC,BD相交于点O,E,F分别为边BC,CD上的动点(点E,F不与线段BC,CD的端点重合)且BE=CF,连接OE,OF,EF.在点E,F运动的过程中,有下列四个结论:
①△OEF是等腰直角三角形;②△OEF面积的最小值是;
③至少存在一个△ECF,使得△ECF的周长是;④四边形OECF的面积是1.
所有符合题意结论的序号是( )
A.①②③ B.③④ C.①②④ D.①②③④
二.填空题(每小题5分,满分20分)
9.将对角线分别为5cm和8cm的菱形改为一个面积不变的正方形,则正方形的边长为 cm.
10.如图,在正方形ABCD中,点E在AB边上,AF⊥DE于点G,交BC于点F.若AE=15,CF=5,则AF的长是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,若AB=6cm,BC=8cm,则△ABO的周长是 cm.
12.如图,菱形ABCD的周长为20,面积为24,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知:如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的面积.
14.如图,△ABC中,AB=AC,AD平分∠BAC,BE∥AD,AE⊥AD.
(1)求证:四边形ADBE是矩形;
(2)作EF⊥AB于F,若BC=4,AD=3,求EF的长.
15.如图,已知矩形ABCD中,AB=4cm,AD=10cm,点P在边BC上移动,点E、F、G、H分别是AB、AP、DP、DC的中点.
(1)求证:EF+GH=5cm;
(2)求当∠APD=90°时,的值.
16.如图,在 ABCD中,M、N分别是AD、BC的中点,∠AND=90°,连接CM交DN于点O.
(1)求证:△ABN≌△CDM;
(2)求证:四边形CDMN为菱形;
(3)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求NC的长.
17.如图,已知正方形ABCD,AB=4,点M在边CD上,射线AM交BD于点E,交射线BC于点F,过点C作CP⊥CE,交AF于点P.
(1)求证:△ADE≌△CDE.
(2)判断△CPF的形状,并说明理由.
(3)作DM的中点N,连结PN,若PN=3,求CF的长.
18.如图,正方形ABCD中,E是CD边的中点,F是BC边上一点,∠FAE=∠DAE.
(1)求证:AF=AD+CF;
(2)已知正方形ABCD的边长为4.
①求AF之长;
②若P是AE上一点,且△DEP是等腰三角形,则线段EP的长为 .
参考答案
一、选择题
1—8:CDCDCBAD
二、填空题
9.【解答】解:∵菱形的对角线分别为5cm和8cm,
∴菱形的面积S5×8=20cm2,
∴正方形的边长是2(cm).
故答案为:2.
10.【解答】解:∵四边形ABCD是正方形,
∴AB=AD=BC,∠B=DAB=90°,
∴∠BAF+∠FAD=90°,
∵AF⊥DE,
∴∠FAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中,
,
∴△BAF≌△ADE(ASA),
∴BF=AE=15,
∵CF=5,
∴BC=BF+CF=20,
∴AB=BC=20,
在Rt△ABF中,AB=20,BF=15,
由勾股定理得:AF25.
故答案为:25.
11.【解答】解:在矩形ABCD中,对角线AC,BD相交于点O,AB=6cm,BC=8cm,
∴∠ABC=90°,OA=OBAC,
∴AC10(cm),
∴AO=BO=5cm,
∴△ABO的周长为OA+OB+AB=16(cm).
故答案为:16.
12.【解答】解:∵菱形ABCD的周长为20,面积为24,
∴AB=AD=5,S△ABD=12,
∵分别作P点到直线AB、AD的垂线段PE、PF,
∴AB×PEPF×AD=12,
∴5×(PE+PF)=12,
∴PE+PF=4.8.
故答案为:4.8.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
∴S菱形BMDN=DM AB=5×4=20.
14.【解答】(1)证明:∵△ABC中,AB=AC,AD平分∠BAC,
∴AD⊥BC,∠ADB=90°,
∵BE∥AD,AE⊥AD,
∴∠DBE=90°,∠DAE=90°,
∴四边形ADBE是矩形;
(2)解:∵AB=AC,AD平分∠BAC,BC=4,AD=3,
∴.
在直角三角形ABD中,由勾股定理得:.
∵四边形ADBE是矩形,
∴BE=AD=3,AE=BD=2.
∵,
∴.
15.【解答】(1)证明:∵矩形ABCD,AD=10cm,
∴BC=AD=10cm.
∵E、F、G、H分别是AB、AP、DP、DC的中点,
∴EF+GHBPPCBC.
∴EF+GH=5cm.
(2)解:∵矩形ABCD,
∴∠B=∠C=90°,
又∵∠APD=90°,
在直角△APD中,AD2=AP2+DP2,
同理,AP2=AB2+BP2,PD2=PC2+CD2=PC2+AB2,
∴AD2=AP2+DP2=AB2+BP2+PC2+DC2=BP2+(BC﹣BP)2+2AB2=BP2+(10﹣BP)2+32,
即100=2BP2﹣20BP+100+32,
解得BP=2或8(cm),
当BP=2时,PC=8,EF=1,GH=4,这时,
当BP=8时,PC=2,EF=4,GH=1,这时,
∴的值为或4.
16.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,,
∴△ABN≌△CDM(SAS);
(2)证明:∵M是AD的中点,∠AND=90°,
∴NM=AM=MD,
∵BN=NC=AM=DM,
∴NC=MN=DM,
∵NC∥DM,NC=DM,
∴四边形CDMN是平行四边形,
又∵MN=DM,
∴四边形CDMN是菱形.
(3)解:∵M是AD的中点,∠AND=90°,
∴MN=MDAD,
∴∠1=∠MND,
∵AD∥BC,
∴∠1=∠CND,
∵∠1=∠2,
∴∠MND=∠CND=∠2,
∴PN=PC,
∵CE⊥MN,
∴∠CEN=90°,
∠END+∠CNP+∠2=180°﹣∠CEN=90°,
又∵∠END=∠CNP=∠2,
∴∠2=∠PNE=30°,
∵PE=1,
∴PN=2PE=2,
∴CE=PC+PE=3,
∴NC2.
17.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE=45°,
在△ADE和△CDE中,
,
∴△ADE≌△CDE(SAS);
(2)解:△CPF是等腰三角形,理由如下:
∵△ADE≌△CDE,
∴∠DAE=∠DCE,
又∵CP⊥CE,DC⊥CF,
∴∠DCE=∠PCF,
又∵AD∥BF,
∴∠DAE=∠CFP,
∴∠PCF=∠PFC,
∴CP=PF,
∴△CPF是等腰三角形;
(3)解:如图,连接DF,
∵∠PCF=∠PFC,
∴∠PCM=∠PMC,
∴PC=MP,
∴MP=PF,
又∵点N是DM的中点,
∴DF=2NP=6,
∴CF2.
18.【解答】(1)证明:如图1,过E点作EG⊥AF,垂足为G,连接EF,
(也可延长AE、BC交于P,用全等和等腰三角形知识解决),
∵EG⊥AF,
∴∠EGF=∠AGE=90°,
∵四边形ABCD是正方形,
∴∠C=∠D=90°,
在△AGE和△ADE中,
∴△AGE≌△ADE(AAS),
∴AD=AG,GE=DE,
∵E是CD边的中点,
∴CE=DE,
∴GE=CE,
在Rt△EGF和Rt△ECF中,
∴Rt△EGF≌Rt△ECF(HL),
∴GF=CF,
∵AF=AG+GF,
∴AF=AD+CF;
(2)解:①设CF=x,则BF=4﹣x,AF=4+x,
在Rt△ABF中,AB2+BF2=AF2,
∴42+(4﹣x)2=(4+x)2,
解得:x=1,
∴AF=4+x=4+1=5;
②分三种情况:
i)如图2,PD=DE,过D作DG⊥AE于G,
∴EP=2EG,
Rt△ADE中,AD=4,DE=2,
∴AE2,
∴S△ADE,
即,
∴DG,
由勾股定理得:EG,
∴EP=2EG;
ii)如图3,EP=DE=2;
iii)如图4,PD=PE,过P作PM⊥DE于M,则DM=EM,
∵AD⊥CD,PM⊥DE,
∴AD∥PM,
∴AP=PE,
∵AE=2,
∴EP,
综上,EP的长是2或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
