第五章特殊平行四边形(A卷)单元测试(含答案)
文档属性
| 名称 | 第五章特殊平行四边形(A卷)单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 729.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 18:29:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章特殊平行四边形(A卷)单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
2.在平行四边形ABCD中,∠B+∠D=80°,则∠A等于( )
A.40° B.80° C.100° D.140°
3.下列说法正确的是( )
A.平行四边形对角线相等 B.矩形的对角线互相垂直
C.菱形的四个角都相等 D.正方形的对角线互相平分
4.已知四边形的四条边长分别为a,b,c,d,其中a,c为一组对边的边长,且满足,则四边形一定是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.无法确定
5.在下列条件中,能够判定 ABCD为菱形的是( )
A.AC=BD B.AC=AD C.AC⊥BD D.AB⊥BC
6.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
A.90° B.45° C.30° D.22.5°
7.如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E,F,则PE+PF的值为( )
A. B. C.5 D.
8.如图,P是矩形ABCD的对角线BD上一点,AB=3,BC=5,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF,则AP+EF的最小值为( )
A. B.4 C. D.8
二.填空题(每小题5分,满分20分)
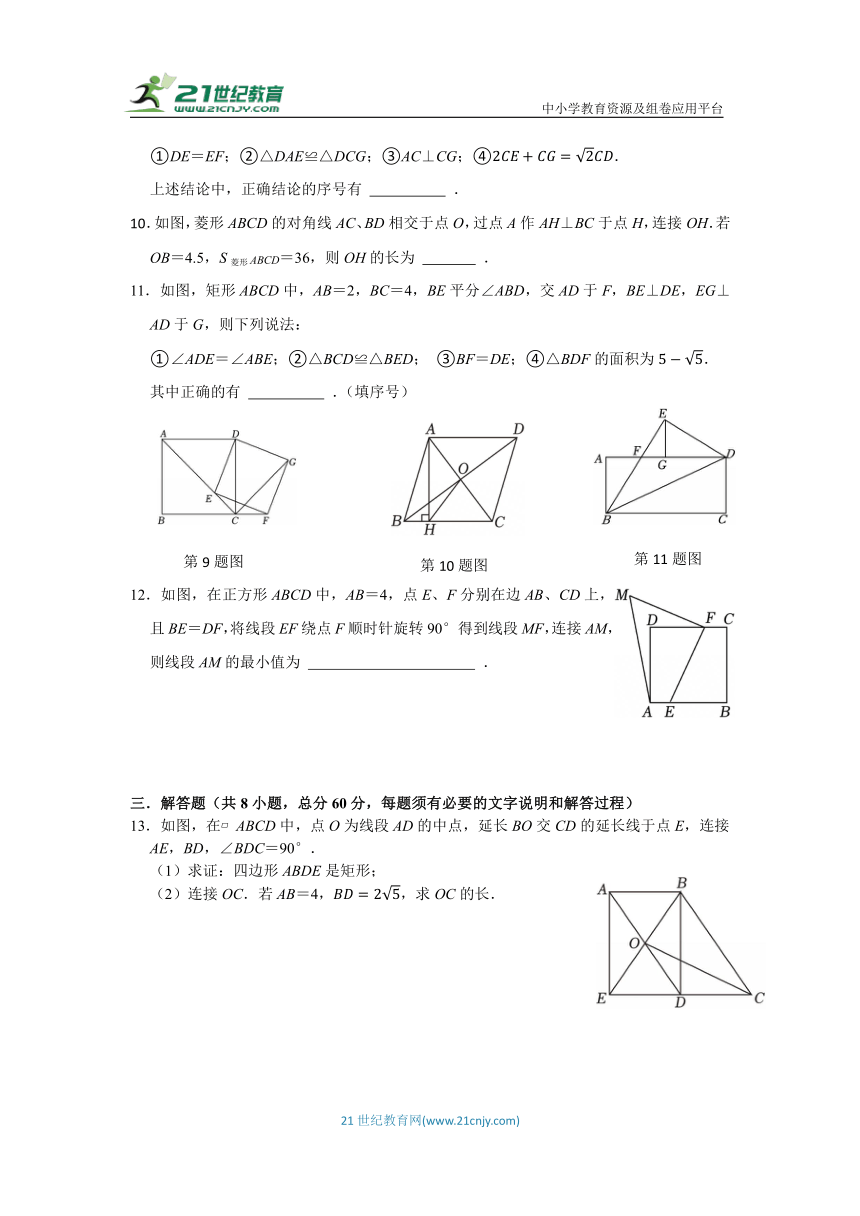
9.如图,点E为正方形ABCD对角线AC上一点,连结DE,过点E作EF⊥DE,交BC延长线于点F,以DE、EF为邻边作矩形DEFG,连结CG.给出下列四个结论:
①DE=EF;②△DAE≌△DCG;③AC⊥CG;④.
上述结论中,正确结论的序号有 .
10.如图,菱形ABCD的对角线AC、BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4.5,S菱形ABCD=36,则OH的长为 .
11.如图,矩形ABCD中,AB=2,BC=4,BE平分∠ABD,交AD于F,BE⊥DE,EG⊥AD于G,则下列说法:
①∠ADE=∠ABE;②△BCD≌△BED; ③BF=DE;④△BDF的面积为.
其中正确的有 .(填序号)
12.如图,在正方形ABCD中,AB=4,点E、F分别在边AB、CD上,且BE=DF,将线段EF绕点F顺时针旋转90°得到线段MF,连接AM,则线段AM的最小值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在 ABCD中,点O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD,∠BDC=90°.
(1)求证:四边形ABDE是矩形;
(2)连接OC.若AB=4,,求OC的长.
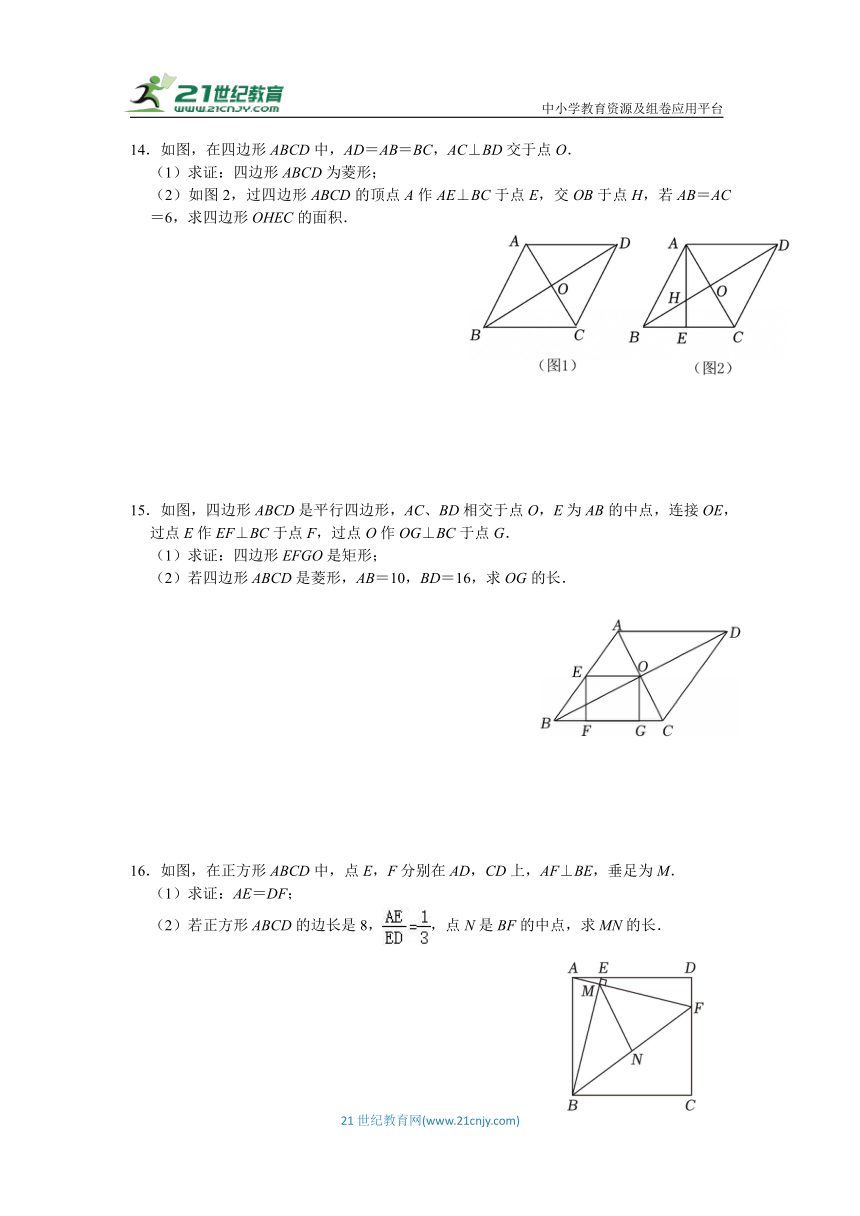
14.如图,在四边形ABCD中,AD=AB=BC,AC⊥BD交于点O.
(1)求证:四边形ABCD为菱形;
(2)如图2,过四边形ABCD的顶点A作AE⊥BC于点E,交OB于点H,若AB=AC=6,求四边形OHEC的面积.
15.如图,四边形ABCD是平行四边形,AC、BD相交于点O,E为AB的中点,连接OE,过点E作EF⊥BC于点F,过点O作OG⊥BC于点G.
(1)求证:四边形EFGO是矩形;
(2)若四边形ABCD是菱形,AB=10,BD=16,求OG的长.
16.如图,在正方形ABCD中,点E,F分别在AD,CD上,AF⊥BE,垂足为M.
(1)求证:AE=DF;
(2)若正方形ABCD的边长是8,,点N是BF的中点,求MN的长.
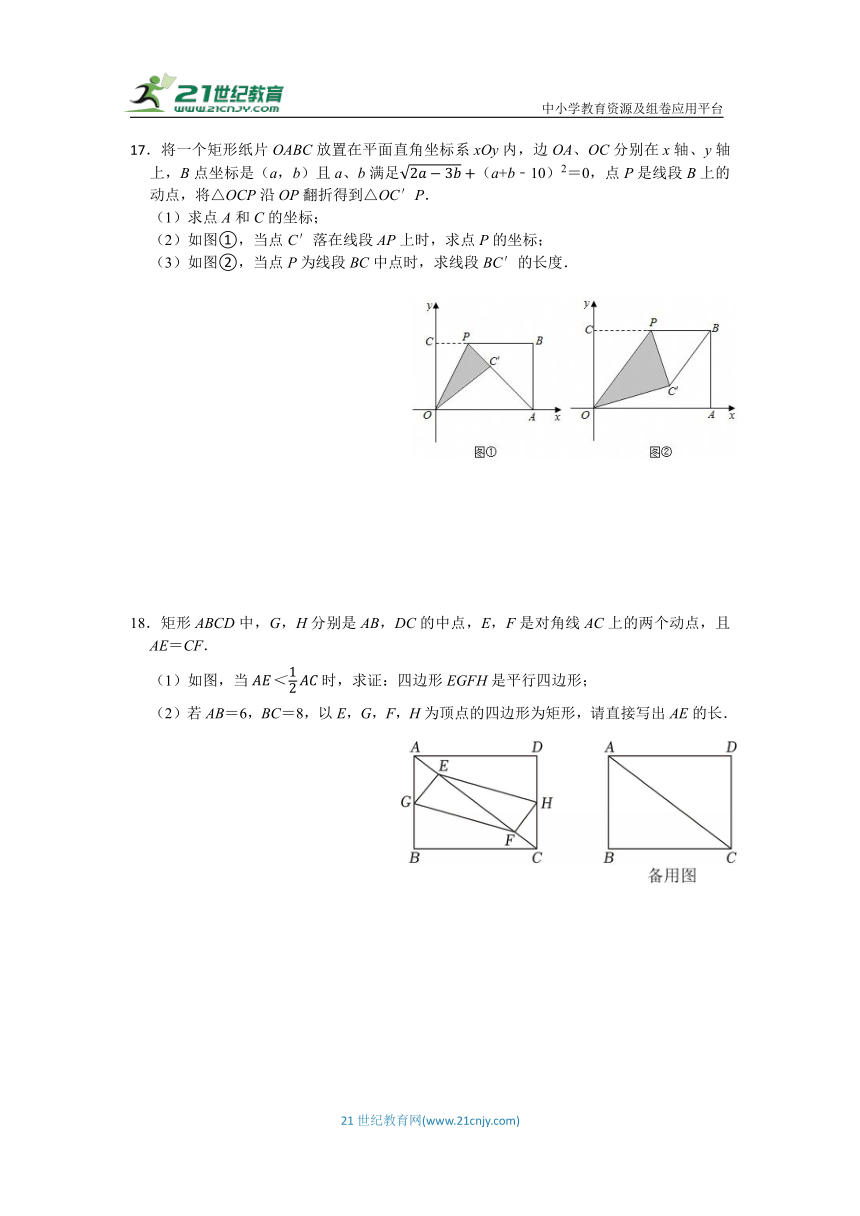
17.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
18.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
参考答案
一、选择题
1—8:CDDBCDBC
二、填空题
9.解:过E作EM⊥BC,过E作EN⊥CD于N,如图所示,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,
∴NE=NC,
∴四边形EMCN是正方形,
∴EM=EN,
∵四边形DEFG是矩形,
∴∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,故①正确;
∴平行四边形DEFG是正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∴AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),故②正确;
∴AE=CG,∠DAE=∠DCG=45°,
∴∠ACG=90°,
∴CG⊥AC,故③正确;
∴AC=AE+CE=CE+CGCD,故④错误;
∴正确结论的序号有①②③,
故答案为:①②③.
10.解:∵四边形ABCD是菱形,OB=4.5,
∴OA=OC,BD=2OB=9,
∵S菱形ABCD=36,
∴,
∴AC=8,
∵AH⊥BC,OA=OC,
∴∠AHC=90°,O为AC的中点;
在Rt△AHC中,O为AC的中点
∴.
故答案为:4.
11.解:∵四边形ABCD是矩形,
∴∠BAD=90°.
∵BE⊥DE,
∴∠DEF=∠BAD=90°,
∵∠AFB=∠DFE,
∴∠ADE=∠ABE,
故①符合题意;
在矩形ABCD中,CD=AB=2,BC=4,
延长DE交BA的延长线于点M,过点E作EN⊥AM于点N,如图所示:
则∠ENA=∠ENM=90°,
在矩形ABCD中,∠BAD=90°,
∴∠NAG=90°,
∵EG⊥AD,
∴∠AGE=∠DGE=90°,
∴四边形AGEN是矩形,
∴AN=GE,NE=AG,
∵BE⊥DE,
∴∠BED=∠BEM=90°,
∵BE平分∠ABD,
∴∠ABE=∠DBE,
在△BED和△BEM中,
,
∴△BED≌△BEM(ASA),
∴BM=BD,ME=DE,
∵∠MAG=∠EGD=90°,
∴AM∥EG,
∴∠M=∠GED,
在△MNE和△EGD中,
,
∴△MNE≌△EGD(AAS),
∴NE=GD,MN=GE,
∴AG=GD=2,
∴AB=GD,
在△ABF和△GDE中,
,
∴△ABF≌△GDE(ASA),
∴BF=DE,AF=GE,
故③符合题意;
∵AB=CD,AB≠DE,
∴△BCD和△BED不全等,
故②不符合题意;
在Rt△BCD中,根据勾股定理,得BD2,
∴BM=BD=2,
∴AM=22,
∴GE=AN=MN1,
∴AF=GE1,
∴DF=4﹣(1)=5,
∴△BDF的面积5,
故④符合题意,
综上所述,符合题意的有①③④,
故答案为:①③④.
12.解:过M作MH⊥AB交BA延长线于H,交CD延长线于T,过E作EF⊥CD于K,如图:
设BE=DF=x,则CF=AE=4﹣x=DK,
∴KF=DF﹣DK=x﹣(4﹣x)=2x﹣4,
∵将线段EF绕点F顺时针旋转90°得到线段MF,
∴MF=EF,∠MFE=90°,
∴∠KFE=90°﹣∠MFT=∠TMF,
∵∠EKF=90°=∠CTM,
∴△EKF≌△FTM(AAS),
∴EK=TF=4,KF=MT=2x﹣4,
∴MH=MT+TH=2x﹣4+4=2x,AH=DT=TF﹣DF=4﹣x,
∴AM,
∴当x时,AM取最小值;
故答案为:.
三、解答题
13.【解答】(1)证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)解:如图,过点O作OF⊥DE于点F,
∵四边形ABDE是矩形,
∴DE=AB=4,ODAD,OB=OEBE,AD=BE,
∴OD=OE,
∵OF⊥DE,
∴DF=EFDE=2,
∴OF为△BDE的中位线,
∴OFBD,
∵四边形ABCD是平行四边形,
∴CD=AB=4,
∴CF=CD+DF=6,
在Rt△OCF中,由勾股定理得:OC,
即OC的长为.
14.【解答】(1)证明:∵AD=AB,AC⊥BD,
∴AC垂直平分BD,
∴BC=CD,
∴BC=CD=AD=AB,
∴四边形ABCD为菱形;
(2)解:如图,连接CH,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC,
∵AB=AC=6,
∴AB=AC=BC=6,
∴△ABC是等边三角形,
∵AE⊥CB,6
∴BE=CE=3,
∴AE,
∵AO=OC,BE=EC,
∴S△AOH=S△OCH=S△ECH=S△BEH,
∴.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
∵EF⊥BC,OG⊥BC,
∴EF∥OG,∠EFG=90°,
∴四边形EFGO是平行四边形,
又∵∠EFG=90°,
∴平行四边形EFGO是矩形;
(2)解:∵四边形ABCD是菱形,BD=16,
∴BC=AB=10,OA=OC,OB=ODBD=8,AC⊥BD,
∴∠BOC=90°,
∴OC6,
由(1)可知,四边形EFGO是矩形,
∴∠OGF=90°,
∴OG⊥BC,
∴S△OBCBC OGOB OC,
∴OG4.8,
即OG的长为4.8.
16.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠BAE=∠ADF=90°,
∵AF⊥BE,
∴∠DAF+∠AEM=90°,
∵∠AEM+∠ABE=90°,
∴∠DAF=∠ABE,
∴△ABE≌△DAF(ASA),
∴AE=DF;
(2)解:∵,
∴ED=3AE,
∴AD=4AE=8,
∴AE=2=DF,
∴CF=6,
∴BF==10,
∵N是中点,∠BMF=90°,
∴MN==5.
17.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
18.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
21世纪教育网(www.21cnjy.com)
第五章特殊平行四边形(A卷)单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
2.在平行四边形ABCD中,∠B+∠D=80°,则∠A等于( )
A.40° B.80° C.100° D.140°
3.下列说法正确的是( )
A.平行四边形对角线相等 B.矩形的对角线互相垂直
C.菱形的四个角都相等 D.正方形的对角线互相平分
4.已知四边形的四条边长分别为a,b,c,d,其中a,c为一组对边的边长,且满足,则四边形一定是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.无法确定
5.在下列条件中,能够判定 ABCD为菱形的是( )
A.AC=BD B.AC=AD C.AC⊥BD D.AB⊥BC
6.如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
A.90° B.45° C.30° D.22.5°
7.如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E,F,则PE+PF的值为( )
A. B. C.5 D.
8.如图,P是矩形ABCD的对角线BD上一点,AB=3,BC=5,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF,则AP+EF的最小值为( )
A. B.4 C. D.8
二.填空题(每小题5分,满分20分)
9.如图,点E为正方形ABCD对角线AC上一点,连结DE,过点E作EF⊥DE,交BC延长线于点F,以DE、EF为邻边作矩形DEFG,连结CG.给出下列四个结论:
①DE=EF;②△DAE≌△DCG;③AC⊥CG;④.
上述结论中,正确结论的序号有 .
10.如图,菱形ABCD的对角线AC、BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4.5,S菱形ABCD=36,则OH的长为 .
11.如图,矩形ABCD中,AB=2,BC=4,BE平分∠ABD,交AD于F,BE⊥DE,EG⊥AD于G,则下列说法:
①∠ADE=∠ABE;②△BCD≌△BED; ③BF=DE;④△BDF的面积为.
其中正确的有 .(填序号)
12.如图,在正方形ABCD中,AB=4,点E、F分别在边AB、CD上,且BE=DF,将线段EF绕点F顺时针旋转90°得到线段MF,连接AM,则线段AM的最小值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在 ABCD中,点O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD,∠BDC=90°.
(1)求证:四边形ABDE是矩形;
(2)连接OC.若AB=4,,求OC的长.
14.如图,在四边形ABCD中,AD=AB=BC,AC⊥BD交于点O.
(1)求证:四边形ABCD为菱形;
(2)如图2,过四边形ABCD的顶点A作AE⊥BC于点E,交OB于点H,若AB=AC=6,求四边形OHEC的面积.
15.如图,四边形ABCD是平行四边形,AC、BD相交于点O,E为AB的中点,连接OE,过点E作EF⊥BC于点F,过点O作OG⊥BC于点G.
(1)求证:四边形EFGO是矩形;
(2)若四边形ABCD是菱形,AB=10,BD=16,求OG的长.
16.如图,在正方形ABCD中,点E,F分别在AD,CD上,AF⊥BE,垂足为M.
(1)求证:AE=DF;
(2)若正方形ABCD的边长是8,,点N是BF的中点,求MN的长.
17.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
18.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
参考答案
一、选择题
1—8:CDDBCDBC
二、填空题
9.解:过E作EM⊥BC,过E作EN⊥CD于N,如图所示,
∵四边形ABCD是正方形,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,
∴NE=NC,
∴四边形EMCN是正方形,
∴EM=EN,
∵四边形DEFG是矩形,
∴∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,故①正确;
∴平行四边形DEFG是正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∴AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),故②正确;
∴AE=CG,∠DAE=∠DCG=45°,
∴∠ACG=90°,
∴CG⊥AC,故③正确;
∴AC=AE+CE=CE+CGCD,故④错误;
∴正确结论的序号有①②③,
故答案为:①②③.
10.解:∵四边形ABCD是菱形,OB=4.5,
∴OA=OC,BD=2OB=9,
∵S菱形ABCD=36,
∴,
∴AC=8,
∵AH⊥BC,OA=OC,
∴∠AHC=90°,O为AC的中点;
在Rt△AHC中,O为AC的中点
∴.
故答案为:4.
11.解:∵四边形ABCD是矩形,
∴∠BAD=90°.
∵BE⊥DE,
∴∠DEF=∠BAD=90°,
∵∠AFB=∠DFE,
∴∠ADE=∠ABE,
故①符合题意;
在矩形ABCD中,CD=AB=2,BC=4,
延长DE交BA的延长线于点M,过点E作EN⊥AM于点N,如图所示:
则∠ENA=∠ENM=90°,
在矩形ABCD中,∠BAD=90°,
∴∠NAG=90°,
∵EG⊥AD,
∴∠AGE=∠DGE=90°,
∴四边形AGEN是矩形,
∴AN=GE,NE=AG,
∵BE⊥DE,
∴∠BED=∠BEM=90°,
∵BE平分∠ABD,
∴∠ABE=∠DBE,
在△BED和△BEM中,
,
∴△BED≌△BEM(ASA),
∴BM=BD,ME=DE,
∵∠MAG=∠EGD=90°,
∴AM∥EG,
∴∠M=∠GED,
在△MNE和△EGD中,
,
∴△MNE≌△EGD(AAS),
∴NE=GD,MN=GE,
∴AG=GD=2,
∴AB=GD,
在△ABF和△GDE中,
,
∴△ABF≌△GDE(ASA),
∴BF=DE,AF=GE,
故③符合题意;
∵AB=CD,AB≠DE,
∴△BCD和△BED不全等,
故②不符合题意;
在Rt△BCD中,根据勾股定理,得BD2,
∴BM=BD=2,
∴AM=22,
∴GE=AN=MN1,
∴AF=GE1,
∴DF=4﹣(1)=5,
∴△BDF的面积5,
故④符合题意,
综上所述,符合题意的有①③④,
故答案为:①③④.
12.解:过M作MH⊥AB交BA延长线于H,交CD延长线于T,过E作EF⊥CD于K,如图:
设BE=DF=x,则CF=AE=4﹣x=DK,
∴KF=DF﹣DK=x﹣(4﹣x)=2x﹣4,
∵将线段EF绕点F顺时针旋转90°得到线段MF,
∴MF=EF,∠MFE=90°,
∴∠KFE=90°﹣∠MFT=∠TMF,
∵∠EKF=90°=∠CTM,
∴△EKF≌△FTM(AAS),
∴EK=TF=4,KF=MT=2x﹣4,
∴MH=MT+TH=2x﹣4+4=2x,AH=DT=TF﹣DF=4﹣x,
∴AM,
∴当x时,AM取最小值;
故答案为:.
三、解答题
13.【解答】(1)证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)解:如图,过点O作OF⊥DE于点F,
∵四边形ABDE是矩形,
∴DE=AB=4,ODAD,OB=OEBE,AD=BE,
∴OD=OE,
∵OF⊥DE,
∴DF=EFDE=2,
∴OF为△BDE的中位线,
∴OFBD,
∵四边形ABCD是平行四边形,
∴CD=AB=4,
∴CF=CD+DF=6,
在Rt△OCF中,由勾股定理得:OC,
即OC的长为.
14.【解答】(1)证明:∵AD=AB,AC⊥BD,
∴AC垂直平分BD,
∴BC=CD,
∴BC=CD=AD=AB,
∴四边形ABCD为菱形;
(2)解:如图,连接CH,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC,
∵AB=AC=6,
∴AB=AC=BC=6,
∴△ABC是等边三角形,
∵AE⊥CB,6
∴BE=CE=3,
∴AE,
∵AO=OC,BE=EC,
∴S△AOH=S△OCH=S△ECH=S△BEH,
∴.
15.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
∵EF⊥BC,OG⊥BC,
∴EF∥OG,∠EFG=90°,
∴四边形EFGO是平行四边形,
又∵∠EFG=90°,
∴平行四边形EFGO是矩形;
(2)解:∵四边形ABCD是菱形,BD=16,
∴BC=AB=10,OA=OC,OB=ODBD=8,AC⊥BD,
∴∠BOC=90°,
∴OC6,
由(1)可知,四边形EFGO是矩形,
∴∠OGF=90°,
∴OG⊥BC,
∴S△OBCBC OGOB OC,
∴OG4.8,
即OG的长为4.8.
16.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠BAE=∠ADF=90°,
∵AF⊥BE,
∴∠DAF+∠AEM=90°,
∵∠AEM+∠ABE=90°,
∴∠DAF=∠ABE,
∴△ABE≌△DAF(ASA),
∴AE=DF;
(2)解:∵,
∴ED=3AE,
∴AD=4AE=8,
∴AE=2=DF,
∴CF=6,
∴BF==10,
∵N是中点,∠BMF=90°,
∴MN==5.
17.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
18.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
