2024-2025学年浙教版数学八年级下册第五单元《特殊平行四边形》单元测试(含答案 )
文档属性
| 名称 | 2024-2025学年浙教版数学八年级下册第五单元《特殊平行四边形》单元测试(含答案 ) |  | |
| 格式 | docx | ||
| 文件大小 | 529.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-04 08:44:08 | ||
图片预览




文档简介
2024-2025学年浙教版数学八年级下册第五单元《特殊平行四边形》
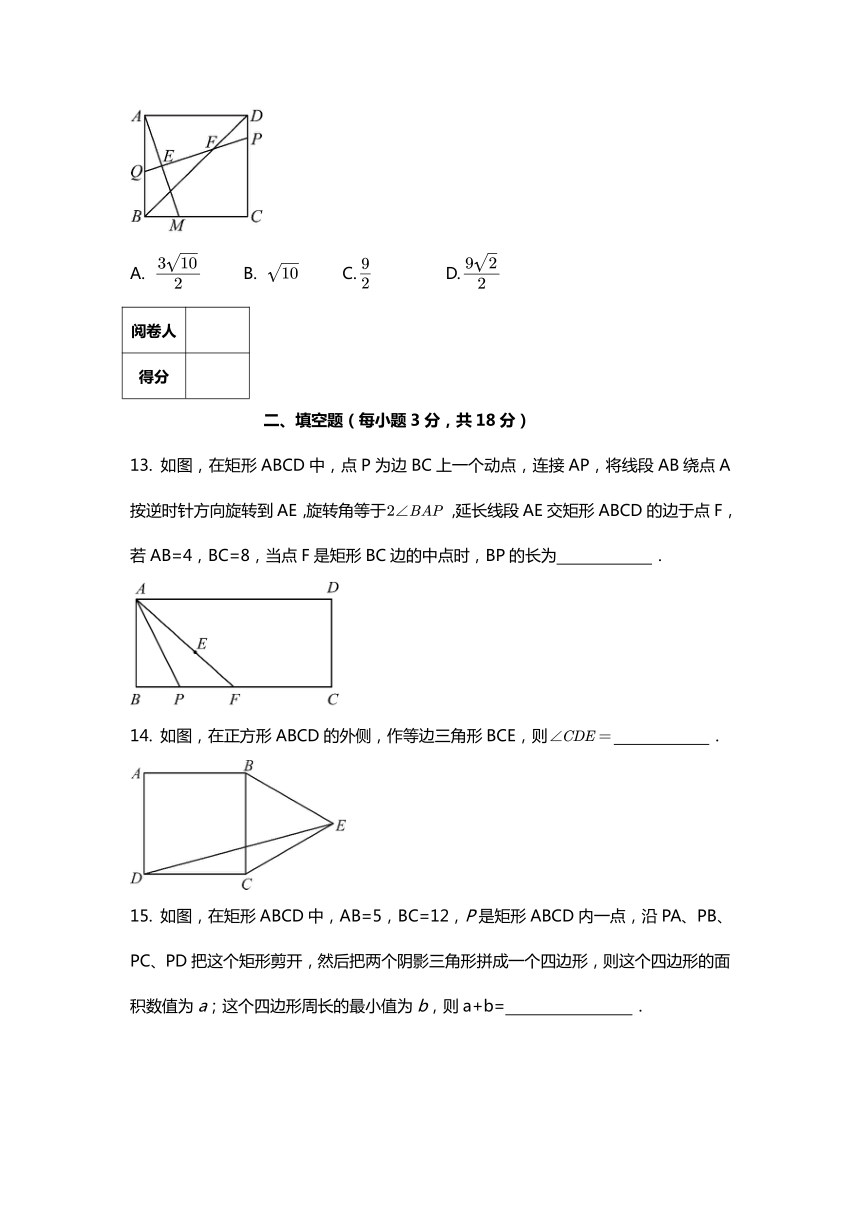
单元练习
【模拟卷01】
考试时间:120分钟 满分:120分
题号 一 二 三 总分
评分
阅卷人
得分
一、选择题(每小题3分,共36分)
1. 下列命题的逆命题中,真命题有( )
①菱形的对角线互相垂直;
②平行四边形的对角线互相平分;
③矩形的对角线相等;
④等腰三角形的两个底角相等.
A.1个 B.2个 C.3个 D.4个
2. 如图,正方形ABCD的面积是5,E、F、P分别是AB、BC、AC上的动点,PE+PF的最小值等于( )
A.5 B. C. D.
3. 如图,菱形ABCD的对角线AC,BD交于点O,过点A作于点E,连接OE,若BD=8, AB=5则OE的长为 ( )
A. 2.5 B.2 C.3.5 D.3
4. 要求加工4个长为4cm、宽为3cm的矩形零件.陈师傅对4个零件进行了检测.根据零件的检测结果,图中不一定能合格的零件是( )
A. B.
C. D.
5. 如图,将一个正方形纸片沿图中虚线剪成四部分,恰能拼成一个没有缝隙且不重叠的等腰三角形,则这个等腰三角形的底边长与正的方形的边长比为( )
A. B. C. D.
6. 直角三角形的两条直角边长分别为6和8,用两个全等的这种直角三角形拼成一个平行四边形,其中最长的对角线是( )
A.10 B. C. D.
7. 如图,在四边形ABCD中,,, , AB=6, AD=4,E、F是BC上的两动点,且EF=4,点E从点B出发,当点F移动到点C时,两点停止运动.在四边形AEFD形状的变化过程中,依次出现的特殊四边形是( )
A.平行四边形→菱形→矩形→平行四边形
B.平行四边形→菱形→正方形→平行四边形
C.平行四边形→菱形→正方形→菱形
D.平行四边形→矩形→菱形→平行四边形
8. 如图,已知矩形纸片ABCD,其中AB=6,BC=8,现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.则CH的长为( )
A. B. C. D.3
9. 如图,已知四边形ABCD为正方形,,E为对角线AC上一点,连接DE,过点E作,交BC的延长线于点F,以DE,EF为邻边作矩形DEFG,连接CG.下列结论:①矩形DEFG是正方形;②CE=CF;③AE=CG;④CE+CG=6.其中结论正确的序号有( )
A.①②③④ B.①③④ C.①②③ D.②③④
10. 如图,在菱形ABCD中,AB=4,,E为AD上一动点,连接BE,以BE为腰作等腰三角形,使得,连结AE’.当AE=3时,的面积为( )
A. B. C. D.3
11. 如图,已知正方形ABCD,AB=10,E为BC边上的一点,连接AE,过点E作且EF=AE,连接DF,以DF为边作正方形DFMN,设正方形DFMN的面积为S,则S的最小值为( )
A.25 B.50 C.75 D.100
12. 如图,正方形纸片的边长为9,折叠正方形纸片ABCD,使得点A落在BC边上的点M,且.折痕PQ交AM于点E,交BD于点F,则QE+PF的值为( )
A. B. C. D.
阅卷人
得分
二、填空题(每小题3分,共18分)
13. 如图,在矩形ABCD中,点P为边BC上一个动点,连接AP,将线段AB绕点A按逆时针方向旋转到AE,旋转角等于,延长线段AE交矩形ABCD的边于点F,若AB=4,BC=8,当点F是矩形BC边的中点时,BP的长为 .
14. 如图,在正方形ABCD的外侧,作等边三角形BCE,则 .
15. 如图,在矩形ABCD中,AB=5,BC=12,P是矩形ABCD内一点,沿PA、PB、PC、PD把这个矩形剪开,然后把两个阴影三角形拼成一个四边形,则这个四边形的面积数值为a;这个四边形周长的最小值为b,则a+b= .
16. 如图,正方形ABCD中,点E,F分别在边CD,AD上,DE=AF,于点G,若BC=8,AF=2,则GF的长为
17. 如图,在矩形ABCD中,E是AD的中点,连接BE,将沿BE翻折得到,EF交BC于点H,延长BF, DC相交于点G.若DG=8,BC=12则FH= .
18. 如图,菱形ABCD的边长为, ,点E,F分别是边AB,BC的中点,连接CE,DF,则CE的长为 , DF的长为 ;
点H,G分别是CE,DF的中点,连接HG,则HG的长为 .
阅卷人
得分
三、解答题(共66分)
19. (本小题6分)如图,在矩形ABCD中 ,AC,BD相交于点O ,E 为AB的中点,连接OE并延长至点F, 使EF=EO, 连接AF,BF.
求证:四边形AFBO是菱形.
20. (本小题10分)如图,正方形ABCD中,点P在对角线BD上,点E在CB的延长线上,且PE=PC,过点P作于F,直线PF分别交AB、CD于G、H.
(1).求证:点F为AE的中点;
(2).若BE=1,AB=3,求PE的长;
(3).求证:.
21. (本小题8分)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG为菱形;
(2)若AG=13,CF=6,求四边形BDFG的周长.
22. (本题8分)如图,在中,点O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD, .
(1).求证:四边形ABDE是矩形;
(2).连接OC,若AB=4,BD=,求OC的长.
23. (本题10分)如图,在四边形ABCD中,,,AD=24cm,BC=26cm,点M从点A出发,以1cm/s的速度向点D运动;点N同时从点C出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.
(1).当运动6s时,判断此时四边形MNCD的形状,并说明理由;
(2).若AB=6cm,且点N的运动速度不变,要使四边形ABNM为正方形,则M点的运动速度是______cm/s;
(3).当MN=CD时,需运动多少时间?
24. (本题12分)如图①,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1).求证:BE=DE;
(2).如图2,过点E作,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,,求正方形DEFG的边长;
(3).若正方形ABCD的边长为,连接CG,如图③,直接写出CE+CG的值.
25. (本小题12分)如图,直线与坐标轴分别交于点A,B,,以OA为边在y轴的右侧作正方形AOBC.
(1).求点A,B的坐标;
(2).如图,点D是x轴上一动点,点E在AD的右侧,∠ADE=90°,AD=DE.
①如图1,问点E是否在定直线上,若是,求该直线的解析式;若不是,请说明理由;
②如图2,点D是线段OB的中点,另一动点H在直线BE上,且∠HAC=∠BAD,请直接写出点H的坐标.
参考答案
一、选择题
1. B . 2. C 3. D 4. C 5. D 6. C 7. A 8.C 9.B 10. C 11.B 12. A
二、填空题
13.
14. 15°
15. 56
16. 5.2
17.
18. 3;;
三、解答题
19. 证明:∵E 为AB的中点,
∴EA=EB,
又∵EF=EO,
∴四边形AFBO是平行四边形,
∵四边形ABCD是矩形,
∴OA=OB,
∴四边形AFBO是菱形.
20. (1)证明:连接AP.
∵四边形ABCD是正方形,
∴AB=BC,,
在△ABP和△CBP中,
,
∴ΔABP ΔCBP(SAS),
∴PA=PC,∠3=∠4
∵PE=PC,
∴PA=PE,
∵PE=PC,
∴∠4=∠5,
∴∠3=∠5,
又∵∠ANP=∠ENB,
∴,
∴,即△APE是等腰直角三角形,
又∵,
∴点F为AE的中点;
(2)题详解
解:在Rt△AEB 中,∠ABE=90°,
∵BE=1,AB=3,
∴
又∵△APE是等腰直角三角形,
∴;
(3)题详解
证明:在DC上截取DM=BE,连接AM,
∵四边形ABCD是正方形,
∴,AB=AD,
在△ABE和△ADM中,
,
∴ΔABE ΔADM(SAS),
∴∠1=∠2,
∴,即.
又∵于F,
∴,
又∵,
∴四边形AGHM是平行四边形,
∴AG=MH,
∵DH=DM+MH,
∴DH=AG+BE.
21. (1) ∵
∴四边形BGFD是平行四边形,
∵CF⊥BD,BD//AG,
∴∠CFA=∠CED=90°,
∵点D是AC中点,
∴DF=AC,
∵∠ABC=90°,BD为AC的中线,
∴BD=AC,
∴BD=DF,
∴平行四边形BGFD是菱形.
(2). 设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,
解得:x=5,x=﹣(舍去),
∵四边形BDFG是菱形,
∴四边形BDFG的周长=4GF=20.
22. (1)题详解
证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)
23. (1)四边形MNCD为平行四边形 (2) (3)6或7
24. (1)题详解
证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)题详解
解:①过点E作于M,于N,如图,
∵正方形ABCD中,∠BCD=90°,
∴四边形EMCN是矩形,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴∠ECM=∠ECN=45°,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°-∠FEN,
在△DEN和△FEM中,
,
,
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②
(3)8
25. (1). A(0,4),B(4,0)
(2). ①是,y=x-4;
②点H坐标为(12, 8)或(6,2)
单元练习
【模拟卷01】
考试时间:120分钟 满分:120分
题号 一 二 三 总分
评分
阅卷人
得分
一、选择题(每小题3分,共36分)
1. 下列命题的逆命题中,真命题有( )
①菱形的对角线互相垂直;
②平行四边形的对角线互相平分;
③矩形的对角线相等;
④等腰三角形的两个底角相等.
A.1个 B.2个 C.3个 D.4个
2. 如图,正方形ABCD的面积是5,E、F、P分别是AB、BC、AC上的动点,PE+PF的最小值等于( )
A.5 B. C. D.
3. 如图,菱形ABCD的对角线AC,BD交于点O,过点A作于点E,连接OE,若BD=8, AB=5则OE的长为 ( )
A. 2.5 B.2 C.3.5 D.3
4. 要求加工4个长为4cm、宽为3cm的矩形零件.陈师傅对4个零件进行了检测.根据零件的检测结果,图中不一定能合格的零件是( )
A. B.
C. D.
5. 如图,将一个正方形纸片沿图中虚线剪成四部分,恰能拼成一个没有缝隙且不重叠的等腰三角形,则这个等腰三角形的底边长与正的方形的边长比为( )
A. B. C. D.
6. 直角三角形的两条直角边长分别为6和8,用两个全等的这种直角三角形拼成一个平行四边形,其中最长的对角线是( )
A.10 B. C. D.
7. 如图,在四边形ABCD中,,, , AB=6, AD=4,E、F是BC上的两动点,且EF=4,点E从点B出发,当点F移动到点C时,两点停止运动.在四边形AEFD形状的变化过程中,依次出现的特殊四边形是( )
A.平行四边形→菱形→矩形→平行四边形
B.平行四边形→菱形→正方形→平行四边形
C.平行四边形→菱形→正方形→菱形
D.平行四边形→矩形→菱形→平行四边形
8. 如图,已知矩形纸片ABCD,其中AB=6,BC=8,现将纸片进行如下操作:第一步,如图①将纸片对折,使AB与DC重合,折痕为EF,展开后如图②;第二步,再将图②中的纸片沿对角线BD折叠,展开后如图③;第三步,将图③中的纸片沿过点E的直线折叠,使点C落在对角线BD上的点H处,如图④.则CH的长为( )
A. B. C. D.3
9. 如图,已知四边形ABCD为正方形,,E为对角线AC上一点,连接DE,过点E作,交BC的延长线于点F,以DE,EF为邻边作矩形DEFG,连接CG.下列结论:①矩形DEFG是正方形;②CE=CF;③AE=CG;④CE+CG=6.其中结论正确的序号有( )
A.①②③④ B.①③④ C.①②③ D.②③④
10. 如图,在菱形ABCD中,AB=4,,E为AD上一动点,连接BE,以BE为腰作等腰三角形,使得,连结AE’.当AE=3时,的面积为( )
A. B. C. D.3
11. 如图,已知正方形ABCD,AB=10,E为BC边上的一点,连接AE,过点E作且EF=AE,连接DF,以DF为边作正方形DFMN,设正方形DFMN的面积为S,则S的最小值为( )
A.25 B.50 C.75 D.100
12. 如图,正方形纸片的边长为9,折叠正方形纸片ABCD,使得点A落在BC边上的点M,且.折痕PQ交AM于点E,交BD于点F,则QE+PF的值为( )
A. B. C. D.
阅卷人
得分
二、填空题(每小题3分,共18分)
13. 如图,在矩形ABCD中,点P为边BC上一个动点,连接AP,将线段AB绕点A按逆时针方向旋转到AE,旋转角等于,延长线段AE交矩形ABCD的边于点F,若AB=4,BC=8,当点F是矩形BC边的中点时,BP的长为 .
14. 如图,在正方形ABCD的外侧,作等边三角形BCE,则 .
15. 如图,在矩形ABCD中,AB=5,BC=12,P是矩形ABCD内一点,沿PA、PB、PC、PD把这个矩形剪开,然后把两个阴影三角形拼成一个四边形,则这个四边形的面积数值为a;这个四边形周长的最小值为b,则a+b= .
16. 如图,正方形ABCD中,点E,F分别在边CD,AD上,DE=AF,于点G,若BC=8,AF=2,则GF的长为
17. 如图,在矩形ABCD中,E是AD的中点,连接BE,将沿BE翻折得到,EF交BC于点H,延长BF, DC相交于点G.若DG=8,BC=12则FH= .
18. 如图,菱形ABCD的边长为, ,点E,F分别是边AB,BC的中点,连接CE,DF,则CE的长为 , DF的长为 ;
点H,G分别是CE,DF的中点,连接HG,则HG的长为 .
阅卷人
得分
三、解答题(共66分)
19. (本小题6分)如图,在矩形ABCD中 ,AC,BD相交于点O ,E 为AB的中点,连接OE并延长至点F, 使EF=EO, 连接AF,BF.
求证:四边形AFBO是菱形.
20. (本小题10分)如图,正方形ABCD中,点P在对角线BD上,点E在CB的延长线上,且PE=PC,过点P作于F,直线PF分别交AB、CD于G、H.
(1).求证:点F为AE的中点;
(2).若BE=1,AB=3,求PE的长;
(3).求证:.
21. (本小题8分)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG为菱形;
(2)若AG=13,CF=6,求四边形BDFG的周长.
22. (本题8分)如图,在中,点O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD, .
(1).求证:四边形ABDE是矩形;
(2).连接OC,若AB=4,BD=,求OC的长.
23. (本题10分)如图,在四边形ABCD中,,,AD=24cm,BC=26cm,点M从点A出发,以1cm/s的速度向点D运动;点N同时从点C出发,以3cm/s的速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.
(1).当运动6s时,判断此时四边形MNCD的形状,并说明理由;
(2).若AB=6cm,且点N的运动速度不变,要使四边形ABNM为正方形,则M点的运动速度是______cm/s;
(3).当MN=CD时,需运动多少时间?
24. (本题12分)如图①,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1).求证:BE=DE;
(2).如图2,过点E作,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,,求正方形DEFG的边长;
(3).若正方形ABCD的边长为,连接CG,如图③,直接写出CE+CG的值.
25. (本小题12分)如图,直线与坐标轴分别交于点A,B,,以OA为边在y轴的右侧作正方形AOBC.
(1).求点A,B的坐标;
(2).如图,点D是x轴上一动点,点E在AD的右侧,∠ADE=90°,AD=DE.
①如图1,问点E是否在定直线上,若是,求该直线的解析式;若不是,请说明理由;
②如图2,点D是线段OB的中点,另一动点H在直线BE上,且∠HAC=∠BAD,请直接写出点H的坐标.
参考答案
一、选择题
1. B . 2. C 3. D 4. C 5. D 6. C 7. A 8.C 9.B 10. C 11.B 12. A
二、填空题
13.
14. 15°
15. 56
16. 5.2
17.
18. 3;;
三、解答题
19. 证明:∵E 为AB的中点,
∴EA=EB,
又∵EF=EO,
∴四边形AFBO是平行四边形,
∵四边形ABCD是矩形,
∴OA=OB,
∴四边形AFBO是菱形.
20. (1)证明:连接AP.
∵四边形ABCD是正方形,
∴AB=BC,,
在△ABP和△CBP中,
,
∴ΔABP ΔCBP(SAS),
∴PA=PC,∠3=∠4
∵PE=PC,
∴PA=PE,
∵PE=PC,
∴∠4=∠5,
∴∠3=∠5,
又∵∠ANP=∠ENB,
∴,
∴,即△APE是等腰直角三角形,
又∵,
∴点F为AE的中点;
(2)题详解
解:在Rt△AEB 中,∠ABE=90°,
∵BE=1,AB=3,
∴
又∵△APE是等腰直角三角形,
∴;
(3)题详解
证明:在DC上截取DM=BE,连接AM,
∵四边形ABCD是正方形,
∴,AB=AD,
在△ABE和△ADM中,
,
∴ΔABE ΔADM(SAS),
∴∠1=∠2,
∴,即.
又∵于F,
∴,
又∵,
∴四边形AGHM是平行四边形,
∴AG=MH,
∵DH=DM+MH,
∴DH=AG+BE.
21. (1) ∵
∴四边形BGFD是平行四边形,
∵CF⊥BD,BD//AG,
∴∠CFA=∠CED=90°,
∵点D是AC中点,
∴DF=AC,
∵∠ABC=90°,BD为AC的中线,
∴BD=AC,
∴BD=DF,
∴平行四边形BGFD是菱形.
(2). 设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,
解得:x=5,x=﹣(舍去),
∵四边形BDFG是菱形,
∴四边形BDFG的周长=4GF=20.
22. (1)题详解
证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)
23. (1)四边形MNCD为平行四边形 (2) (3)6或7
24. (1)题详解
证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)题详解
解:①过点E作于M,于N,如图,
∵正方形ABCD中,∠BCD=90°,
∴四边形EMCN是矩形,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴∠ECM=∠ECN=45°,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°-∠FEN,
在△DEN和△FEM中,
,
,
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②
(3)8
25. (1). A(0,4),B(4,0)
(2). ①是,y=x-4;
②点H坐标为(12, 8)或(6,2)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
