第四章平行四边形单元测试A卷(含答案)
文档属性
| 名称 | 第四章平行四边形单元测试A卷(含答案) | 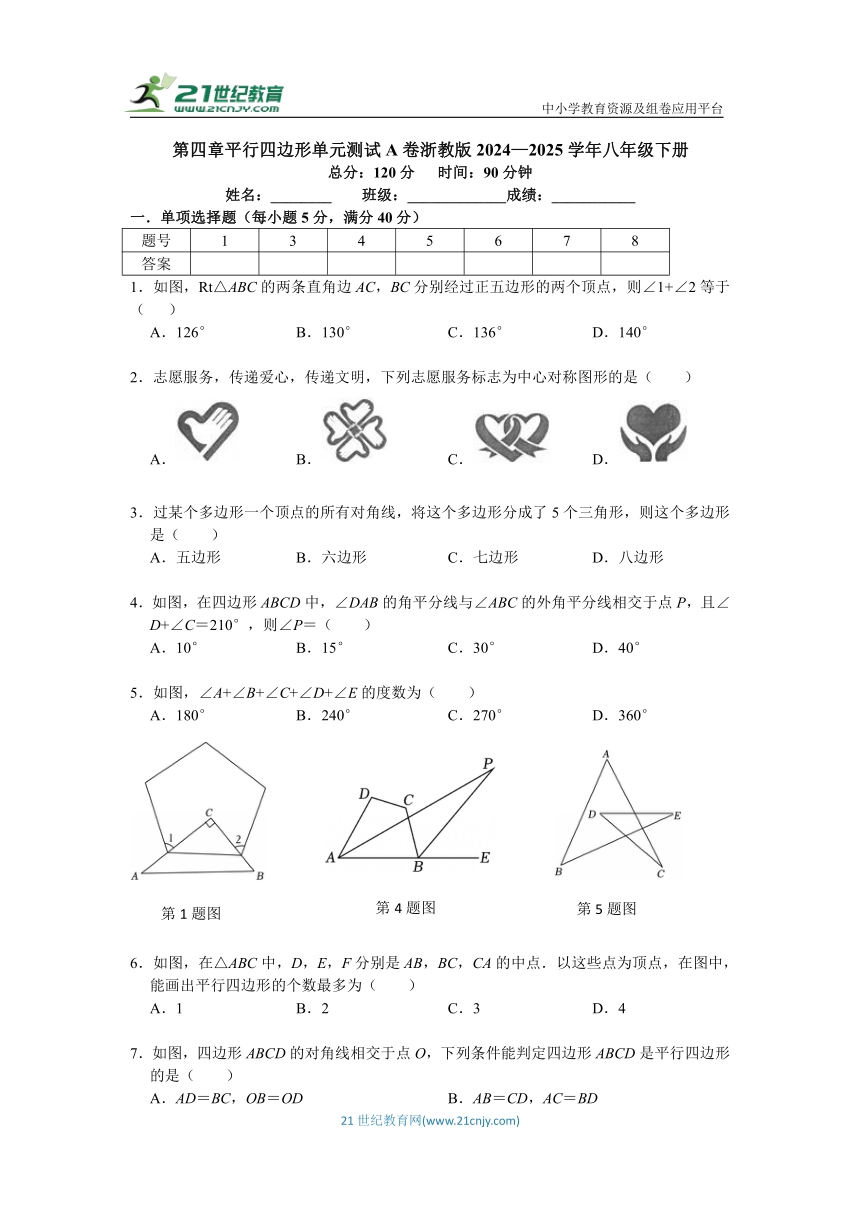 | |
| 格式 | docx | ||
| 文件大小 | 571.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 17:19:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第四章平行四边形单元测试A卷浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.如图,Rt△ABC的两条直角边AC,BC分别经过正五边形的两个顶点,则∠1+∠2等于( )
A.126° B.130° C.136° D.140°
2.志愿服务,传递爱心,传递文明,下列志愿服务标志为中心对称图形的是( )
A. B. C. D.
3.过某个多边形一个顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=( )
A.10° B.15° C.30° D.40°
5.如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.240° C.270° D.360°
6.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点.以这些点为顶点,在图中,能画出平行四边形的个数最多为( )
A.1 B.2 C.3 D.4
7.如图,四边形ABCD的对角线相交于点O,下列条件能判定四边形ABCD是平行四边形的是( )
A.AD=BC,OB=OD B.AB=CD,AC=BD
C.AB∥CD,OA=OC D.AB=CD,BC∥AD
8.如图,在腰长为8的等腰△ABC中,AB=AC,E,M,F分别是AB,BC,AC上的点,并且ME∥AC,MF∥AB,则四边形MEAF的周长是( )
A.8 B.10 C.12 D.16
二.填空题(每小题5分,满分20分)
9.如图,在平面直角坐标系中,平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),则顶点B的坐标为 .
10.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为 .
11.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=17cm2,S△BQC=27cm2,则阴影部分的面积为 cm2.
12.平行四边形两邻边的长为3和4,两对角线长为m,n,则m2+n2的值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OEEC;
(2)若OD=2,求AB的长.
14.如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
15.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
16.已知:如图,在平行四边形ABCD中,对角线BD,AC相交于点O,点E,F分别在BD,DB的延长线上,且DE=BF,连接AE,AF,CF,CE.
(1)求证:四边形AFCE为平行四边形;
(2)若AC平分∠EAF,∠AEC=60°,OA=4,求四边形AFCE的周长.
17.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,EF=DC.
(1)求证:四边形EFCD是平行四边形.
(2)连结BE,若BE=EF,AD=6,求AE的长度.
18.如图,在 ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长.
参考答案
一、选择题
1—8:ABCBACCD
二、填空题
9.【解答】解:设B点的坐标为(x,y),
∵平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),
∴,
解得x=3,y=﹣1,
∴B(3,﹣1).
故答案为:(3,﹣1).
10.【解答】解:当P点在BA上,BP=BE=6,
作BH⊥PE于H,如图1,则PH=EH,
∵∠B=120°,
∴∠BPE=∠BEP=30°,
在Rt△BEH中,BHBE=3,EHBH=3,
∴PE=2EH=6;
当P点在AD上,BP=PE,
作BG⊥AD于G,PF⊥BE于F,如图2,则BF=EF=3,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵∠ABC=120°,
∴∠A=60°,
在Rt△ABG中,AGAB=4,BGAG=4,
∴PF=4,
在Rt△PEF中,PE;
当点P在CD上,如图3,EB=EP=6,
综上所述,PE的长为6或6或.
故答案为6或6或.
11.【解答】解:如图,连接EF
∵△ADF与△DEF同底等高,
∴S△ADF=S△DEF,
即S△ADF﹣S△DPF=S△DEF﹣S△DPF,
即S△APD=S△EPF=17cm2,
同理可得S△BQC=S△EFQ=27cm2,
∴阴影部分的面积为S△EPF+S△EFQ=17+27=44cm2.
故答案为:44.
12.【解答】解:设 ABCD中,AB=3,BC=4,AC=m,BD=n,
作AE⊥BC,DF⊥BC,垂足分别为E,F,如图所示,
在 ABCD中,AD∥BC,CD=AB=3,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠AEC=∠DFB=90°,AE∥DF,
∴四边形AEFD是平行四边形,
∴AE=DF,EF=AD=BC=4,
∴BE=CF,
在Rt△ABE中,AE2+BE2=AB2=9,
在Rt△AEC中,AE2+EC2=AC2=m2,
在Rt△DCF中,DF2+CF2=CD2=9,
在Rt△BFD中,DF2+BF2=BD2=n2,
∴m2+n2
=AE2+EC2+DF2+BF2
=AE2+(4﹣BE)2+DF2+(4+CF)2
=AE2+16﹣8BE+BE2+DF2+16+8CF+CF2
=32+(AE2+BE2)+(DF2+CF2)
=32+9+9
=50,
故答案为:50.
三、解答题
13.【解答】(1)证明:∵ED,EF是中位线,
∴ED∥FC,EF∥DC,
∴四边形EFCD是平行四边形,
∵对角线CE和DF相交于点O,
∴OE;
(2)解:∵EC,DF是平行四边形EFCD的对角线,OD=2,
∴DF=2OD=4,
∵ED,EF是△ABC的中位线,
∴点D,F分别是AC,BC的中点,
∴DF是△ABC的中位线,
∴DF,
∴AB=2DF=8.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长CD至点E,使CD=DE,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(2)解:连接OE,
∵ ABCD的对角线AC与BD相交于点O,AC=8,
∴OA=OCAC=4,
∵AC平分∠BAE,
∴∠BAC=∠EAC,
∵AB∥CD,
∴∠BAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=CE=6,
∴OE⊥AC,
∴∠AOE=90°,
∴OE2,
∴S△ACEAC OE8×28,
∴△ACE的面积是8.
15.【解答】(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
16.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴OD=OB,
∵DE=BF,
∴OD+DE=OB+BF,
∴OE=OF,
∵OA=OC,
∴四边形AFCE为平行四边形.
(2)解:∵AC平分∠EAF,
∴∠EAC=∠FAC,
∵四边形AFCE为平行四边形,OA=4,
∴CE∥AF,OC=OA=4,
∴∠ECA=∠FAC,AC=4+4=8,
∴∠EAC=∠ECA,
∴AE=CE,
∴四边形AFCE是菱形,
∵∠AEC=60°,
∴△EAC是等边三角形,
∴AE=AC=8,
∴AF+CF+CE+AE=4AE=4×8=32,
∴四边形AFCE周长是32.
17.【解答】(1)证明:∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC,
∵EF=DC,
∴四边形EFCD是平行四边形;
(2)解:连接BE,如图所示:
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠FBE=60°,
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠ABE=∠ACD,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴AE=AD=6.
18.【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
∵AE=CF,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=10,
∴OB=OD=5,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB=2.5.
∴EG的长为2.5.
21世纪教育网(www.21cnjy.com)
第四章平行四边形单元测试A卷浙教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.如图,Rt△ABC的两条直角边AC,BC分别经过正五边形的两个顶点,则∠1+∠2等于( )
A.126° B.130° C.136° D.140°
2.志愿服务,传递爱心,传递文明,下列志愿服务标志为中心对称图形的是( )
A. B. C. D.
3.过某个多边形一个顶点的所有对角线,将这个多边形分成了5个三角形,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=210°,则∠P=( )
A.10° B.15° C.30° D.40°
5.如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.240° C.270° D.360°
6.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点.以这些点为顶点,在图中,能画出平行四边形的个数最多为( )
A.1 B.2 C.3 D.4
7.如图,四边形ABCD的对角线相交于点O,下列条件能判定四边形ABCD是平行四边形的是( )
A.AD=BC,OB=OD B.AB=CD,AC=BD
C.AB∥CD,OA=OC D.AB=CD,BC∥AD
8.如图,在腰长为8的等腰△ABC中,AB=AC,E,M,F分别是AB,BC,AC上的点,并且ME∥AC,MF∥AB,则四边形MEAF的周长是( )
A.8 B.10 C.12 D.16
二.填空题(每小题5分,满分20分)
9.如图,在平面直角坐标系中,平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),则顶点B的坐标为 .
10.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为 .
11.如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=17cm2,S△BQC=27cm2,则阴影部分的面积为 cm2.
12.平行四边形两邻边的长为3和4,两对角线长为m,n,则m2+n2的值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OEEC;
(2)若OD=2,求AB的长.
14.如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
15.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
16.已知:如图,在平行四边形ABCD中,对角线BD,AC相交于点O,点E,F分别在BD,DB的延长线上,且DE=BF,连接AE,AF,CF,CE.
(1)求证:四边形AFCE为平行四边形;
(2)若AC平分∠EAF,∠AEC=60°,OA=4,求四边形AFCE的周长.
17.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,EF=DC.
(1)求证:四边形EFCD是平行四边形.
(2)连结BE,若BE=EF,AD=6,求AE的长度.
18.如图,在 ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长.
参考答案
一、选择题
1—8:ABCBACCD
二、填空题
9.【解答】解:设B点的坐标为(x,y),
∵平行四边形ABCD三个顶点坐标分别为A(﹣1,﹣2),D(1,1),C(5,2),
∴,
解得x=3,y=﹣1,
∴B(3,﹣1).
故答案为:(3,﹣1).
10.【解答】解:当P点在BA上,BP=BE=6,
作BH⊥PE于H,如图1,则PH=EH,
∵∠B=120°,
∴∠BPE=∠BEP=30°,
在Rt△BEH中,BHBE=3,EHBH=3,
∴PE=2EH=6;
当P点在AD上,BP=PE,
作BG⊥AD于G,PF⊥BE于F,如图2,则BF=EF=3,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵∠ABC=120°,
∴∠A=60°,
在Rt△ABG中,AGAB=4,BGAG=4,
∴PF=4,
在Rt△PEF中,PE;
当点P在CD上,如图3,EB=EP=6,
综上所述,PE的长为6或6或.
故答案为6或6或.
11.【解答】解:如图,连接EF
∵△ADF与△DEF同底等高,
∴S△ADF=S△DEF,
即S△ADF﹣S△DPF=S△DEF﹣S△DPF,
即S△APD=S△EPF=17cm2,
同理可得S△BQC=S△EFQ=27cm2,
∴阴影部分的面积为S△EPF+S△EFQ=17+27=44cm2.
故答案为:44.
12.【解答】解:设 ABCD中,AB=3,BC=4,AC=m,BD=n,
作AE⊥BC,DF⊥BC,垂足分别为E,F,如图所示,
在 ABCD中,AD∥BC,CD=AB=3,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠AEC=∠DFB=90°,AE∥DF,
∴四边形AEFD是平行四边形,
∴AE=DF,EF=AD=BC=4,
∴BE=CF,
在Rt△ABE中,AE2+BE2=AB2=9,
在Rt△AEC中,AE2+EC2=AC2=m2,
在Rt△DCF中,DF2+CF2=CD2=9,
在Rt△BFD中,DF2+BF2=BD2=n2,
∴m2+n2
=AE2+EC2+DF2+BF2
=AE2+(4﹣BE)2+DF2+(4+CF)2
=AE2+16﹣8BE+BE2+DF2+16+8CF+CF2
=32+(AE2+BE2)+(DF2+CF2)
=32+9+9
=50,
故答案为:50.
三、解答题
13.【解答】(1)证明:∵ED,EF是中位线,
∴ED∥FC,EF∥DC,
∴四边形EFCD是平行四边形,
∵对角线CE和DF相交于点O,
∴OE;
(2)解:∵EC,DF是平行四边形EFCD的对角线,OD=2,
∴DF=2OD=4,
∵ED,EF是△ABC的中位线,
∴点D,F分别是AC,BC的中点,
∴DF是△ABC的中位线,
∴DF,
∴AB=2DF=8.
14.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长CD至点E,使CD=DE,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(2)解:连接OE,
∵ ABCD的对角线AC与BD相交于点O,AC=8,
∴OA=OCAC=4,
∵AC平分∠BAE,
∴∠BAC=∠EAC,
∵AB∥CD,
∴∠BAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=CE=6,
∴OE⊥AC,
∴∠AOE=90°,
∴OE2,
∴S△ACEAC OE8×28,
∴△ACE的面积是8.
15.【解答】(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
16.【解答】(1)证明:∵四边形ABCD为平行四边形,
∴OD=OB,
∵DE=BF,
∴OD+DE=OB+BF,
∴OE=OF,
∵OA=OC,
∴四边形AFCE为平行四边形.
(2)解:∵AC平分∠EAF,
∴∠EAC=∠FAC,
∵四边形AFCE为平行四边形,OA=4,
∴CE∥AF,OC=OA=4,
∴∠ECA=∠FAC,AC=4+4=8,
∴∠EAC=∠ECA,
∴AE=CE,
∴四边形AFCE是菱形,
∵∠AEC=60°,
∴△EAC是等边三角形,
∴AE=AC=8,
∴AF+CF+CE+AE=4AE=4×8=32,
∴四边形AFCE周长是32.
17.【解答】(1)证明:∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠EFB=60°,
∴∠ABC=∠EFB,
∴EF∥DC,
∵EF=DC,
∴四边形EFCD是平行四边形;
(2)解:连接BE,如图所示:
∵BF=EF,∠EFB=60°,
∴△EFB是等边三角形,
∴EB=EF,∠FBE=60°,
∵DC=EF,
∴EB=DC,
∵△ABC是等边三角形,
∴∠ACB=60°,AB=AC,
∴∠ABE=∠ACD,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴AE=AD=6.
18.【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
∵AE=CF,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=10,
∴OB=OD=5,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EGOB=2.5.
∴EG的长为2.5.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
